矢量矩阵处理在海面水声处理中的应用
2015-02-22崔秀梅
崔秀梅
(烟台汽车工程职业学院,山东烟台265500)
矢量矩阵处理在海面水声处理中的应用
崔秀梅
(烟台汽车工程职业学院,山东烟台265500)
摘要:从最小二乘法的思想出发,研究海面上多干扰信号产生的无法探测区域及干扰信号和有用信号频谱无法区别的情形下,利用矩阵滤波器来抑制海上多目标干扰的情况,通过矢量矩阵对水下目标准确定位,实现有用信号的快速识别,最后通过实验证明本方法的有效性。
关键词:矢量矩阵;最小二乘法;水声信号处理;矩阵滤波器
Application of vector matrix in underwater acoustic signal processing
CUI Xiu-mei
(Yantai Aotomobile Engineering Professional College,Yantai 265500,China)
Abstract:In this paper,starting from the least squares method studied that the region couldnot be detected on the sea more interfering signal and spectral of interference signal and useful signal indistinguishable under circumstances.Using matrix filter to suppress maritime multi-target interference.By using matrix accurately to locate underwater targets.Realize quickly identify the useful signal.Final the experimental results show the effectiveness of the method.
Key words:vector matrix; the least square method; underwater acoustic signal processing;matrix filter
0 引言
随着科技的发展,世界各国越来越意识到开发海洋资源的必要性。海洋环境具有很大的不确定性,受到风浪流等因素的影响,同时舰船的辐射信号中也含有海洋环境中的噪声,从而需要从中提取出舰船的固有信息,因而水声信号的处理技术得到广泛重视。Vaccaaro等[1]利用矢量矩阵抑制深海中不感兴趣的干扰噪声,同时尽量的使感兴趣的信号保持原样。鄢社峰等[2]从广义滤波器出发,利用恒定阻带抑制矩阵滤波器对深度域上的信号进行滤波抑制匹配噪声。
本文从最小二乘法的思想出发,研究海面上多干扰信号产生的无法探测的区域以及干扰信号和有用信号的频谱无法区别的情形下,利用矩阵滤波器来抑制海上多目标干扰的情况,通过矢量矩阵对水下目标准确定位,实现了有用信号的快速识别,最后通过实验证明本方法的有效性。
1 最小二乘矩阵滤波器设计原理
设垂直指向的水听器是K元且每个间距为d。如图1所示,在海中存在1个目标源和2个干扰源。
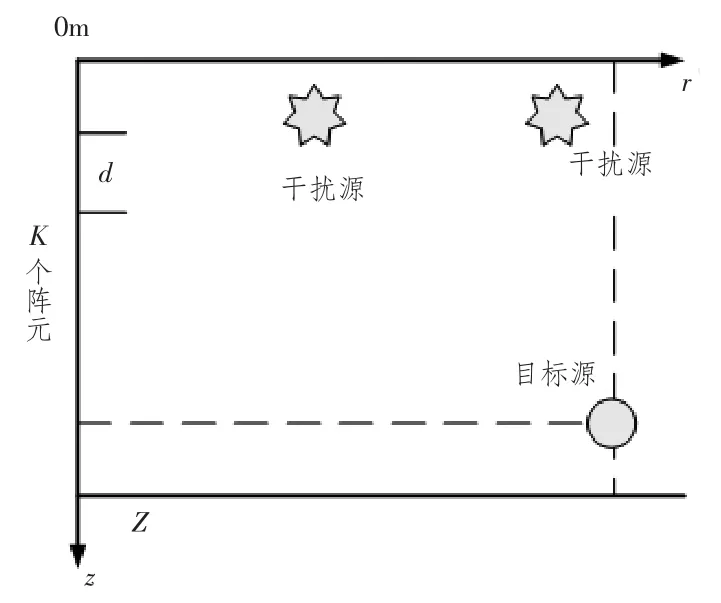
图1 K元垂直指向水听器模型Fig.1 K vertically oriented hydrophone model
按距离和深度划分实验海域,距离域上的网格数为M,深度域上的网格数为N。令第(m,n)个网格的拷贝向量为v(m,n),则感兴趣区域的向量为v(mp,np),不感兴趣区域的向量为v(ms,ns)。一般在感兴趣区域和不感兴趣区域有一个过渡区,是为了防止二者产生突然变化。
设矩阵滤波器H的维数为K×K,对均匀线性阵列进行阵元滤波,则输出v0(m,n) :
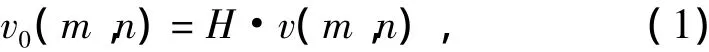
因此对矩阵滤波器的设计可用下式进行表达:
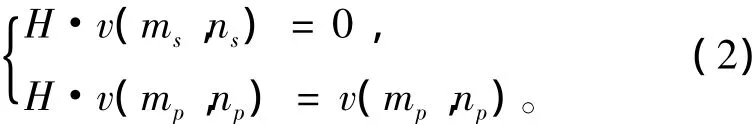
通过设置矩阵滤波器的幅度频谱来调节滤波器得到最好输出效果。
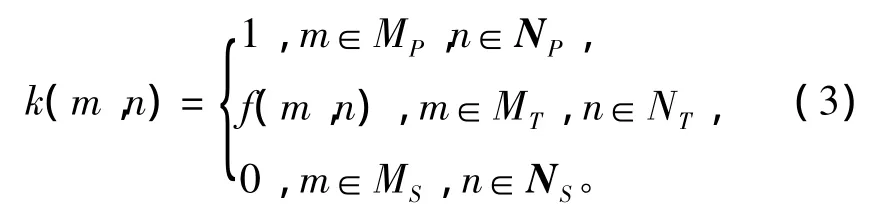
式中: MP,MT,MS,NP,NT,NS分别为感兴趣区域、不感兴趣区域和过渡区的拷贝向量在距离和深度上所对应的网点数集。
拷贝向量v(m,n)与其经过滤波器后得到期望幅度限制系数k(m,n)的关系为:
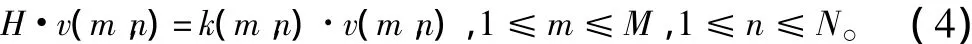
令整个试验区域的拷贝向量集合为:
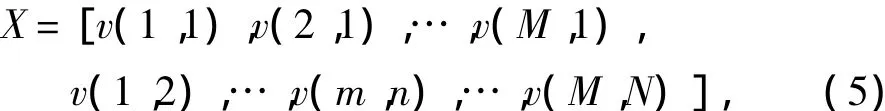
由上式可看出向量是K×MN维。经过滤波器后得到的期望响应是:

故此在设计滤波器时应满足HX=Y,令
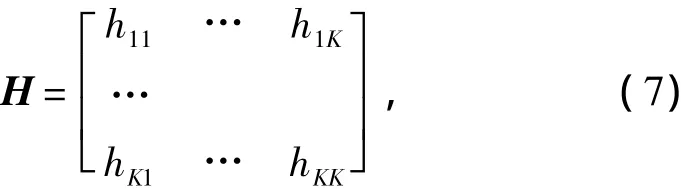
计算得到K2×1维向量
y=[h11,h12,…,h1K,h21,从而可以得到重构矩阵滤波器H。
拷贝向量v(m,n)经过矩阵滤波器可得到H· v(m,n) = k(m,n)·v(m,n),其转化为:
则矩阵滤波器的问题HX =Y即变为求取线性方程组解的问题V·y = b。
该方程组的方程个数为KMN,未知数的个数为K2,方程组的解取决于系数矩阵V的秩,若KMN>K2且V满秩,则说明线性方程组存在最小二乘解。
求取rank(V) :

对矩阵X进行奇异值分解时,奇异值都非零,且M·N>>K,以及rank(X) = K,故rank(V) = K× rank(XT) =K2。当矩阵的最大值和最小值的比值越接近1,则矩阵越稳定,滤波器的效果越好。
于是可以根据误差平方和最小求出V·y=b的最小二乘解[3]。
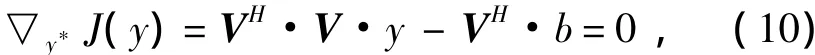
式中(·)*为矩阵的共轭,则误差平方和方程为:
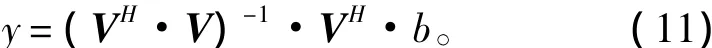
于是可得矩阵滤波器H:

通过式(11)计算y的运算量非常大,结算速度慢,利用简化求得拷贝向量矩阵[4-5]。


由此可得,最小二乘矩阵滤波器H是期望的拷贝向量矩阵与原先拷贝向量矩阵右伪逆相乘得到的。
2 实验结果
通过以上实验验证本文算法的有效性,设有50个阵元,每2个阵元之间的相隔2 m,滤波器不感兴趣区域距离水听器1~10 km,深度[0,10 m],过渡区域为[10 m,16 m],感兴趣的区域为10 m以上,在600~750 Hz频段内构造了最小二乘矩阵滤波器,然后将获得的船舶噪声和海面上的噪声混合信号进行时域分析,分别获得有用信号和干扰信号的线谱,并将其作为拷贝向量的频点。船舶有用信号与干扰信号构成的混合信号的频谱如图2所示。
通常情况下海面上的干扰噪声在有些线谱上的声源级弱于有用信号,故本文在600~750 Hz频段内利用全频段滤波的方法进行信号的区分识别,识别率如表1所示。
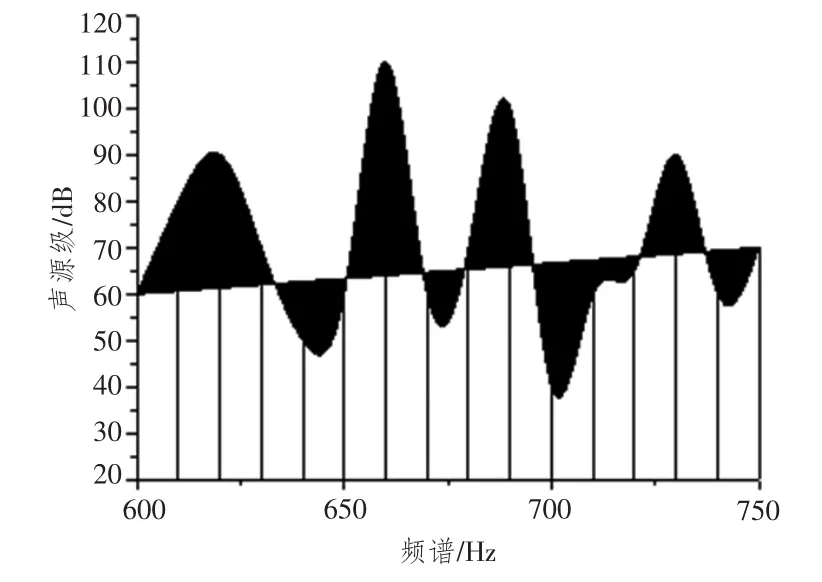
图2 混合信号频谱图Fig.2 Mixed-signal spectrum

表1 识别率对比表Tab.1 Recognition rate comparison table
由表1可看出,通过全频段的滤波能够极大地提高有用信号和噪声的识别率,有利于频谱图上准确的定位线谱。从而说明了矢量矩阵滤波器可以抑制海上多干扰源对有用信号的干扰。
3 结语
本文从最小二乘法的理思想出发,研究海面上多干扰信号产生的无法探测的区域以及干扰信号和有用信号的频谱无法区别的情形下,利用矩阵滤波器来抑制海上多目标干扰的情况,通过矢量矩阵对水下目标准确定位,实现了有用信号的快速识别,最后通过实验证明了本方法的有效性。
参考文献:
[1]VACCARO R J,CHHETRI A,HARRISON B F.Matrix filter design for passive sonar interference suppression[J].J.Acoustic Soc.Am.,2001,115(6) :3010-3020.
[2]鄢社锋,马远良.匹配场噪声抑制:广义空域滤波方法[J].科学通报,2001,49(18) :1909-1912.
[3]徐驰,韩磊,张书第,等.最小二乘矩阵滤波器设计与性能分析[J].舰船科学技术,2011,33(4) :72-76.
[4]POTER M B.The KRAKEN normal mode program[R].[S.L]: Naval Reseach Laboratory,1991.
[5]BAGGEROER A B,KUPERMAN W A,MIKHALEVSKY P N.An overview of matched field methods in ocean acoustics [J].IEEE J.Ocean Eng.,1993,18(4) :401-424.
作者简介:崔秀梅(1968-),女,本科,副教授,研究方向为基础数学、数学建模及应用。
收稿日期:2014-12-07;修回日期: 2015-03-05
文章编号:1672-7649(2015) 07-0157-03doi:10.3404/j.issn.1672-7649.2015.07.036
中图分类号:U665.26
文献标识码:A
