基于FPM的液舱晃荡研究

郑亚雄，王明振，史圣哲

(中国特种飞行器研究所水动力研究中心，湖北荆门448035)

基于FPM的液舱晃荡研究

郑亚雄，王明振，史圣哲

(中国特种飞行器研究所水动力研究中心，湖北荆门448035)

摘要:随着液舱晃荡运动机理的研究深入，舱内液体运动响应和自由液面波形精细模拟成为研究的重点。本文应用无网格方法中的FPM(Finite Point Method)来对液舱晃荡中的动边界及自由液面大变形等问题进行数值求解和图像模拟。以二维液舱晃荡为例，校核运动边界与内部流体粒子点间的运动响应，得到FPM对于边界所受砰击力和内部兴波波高的计算结果以及自由液面模拟图像。将计算结果进行无因次化处理，通过与试验结果进行比对，验证了FPM在液舱晃荡问题中应用的可行性和准确性，也为FPM解决三维复杂液舱晃荡问题中提供铺垫。

关键词:FPM;液舱晃荡;自由液面;动边界

Research on sloshing of liquid tank based on FPM

ZHENG Ya-xiong，WANG Ming-zhen，SHI Sheng-zhe
(Hydrodynamic Research Center，AVIC Special Vehicle Research Institute，Jingmen 448035，China)

Abstract:With the development of research on sloshing of liquid tank，the motion response and the free surface wave simulation have been focused．In this paper，FPM (Finite Point Method) has been applied into numerical calculation of sloshing in the moving boundary and simulation of free surface deformation．Taking the two－dimensional sloshing tank as an example，interactional response between moving boundary and internal fluid particle points has been checked．Slamming force on boundary，internal wave height and image of free surface have been attained．Taking the computational results into dimensionless，the comparison with the experimental results verify the feasibility and accuracy of application of FPM in the liquid sloshing，and pave the way for FPM to solve the complex 3D liquid sloshing．

Key words:FPM; sloshing of liquid tank; free surface;moving boundary

0　引言

随着海上运输的发展，液货船得到广泛的应用，液舱内液体晃荡所引起的砰击压力对船舶性能有很大的影响。晃荡液体的运动具有很强的非线性特性，当舱壁做规律性很强的简谐运动时，液舱内液体受到简谐激励，由此反馈激发的砰击作用的持续时间和所产生的兴波幅值跟着时间来变化。晃荡所激发的砰击力的幅值大小很难去做实时准确的预报，只能从统计角度上进行大小的估计。在容器晃荡时，当外界激励频率接近内部带自由液面液体的固有频率时，液体的运动则会十分激烈，尤其是在接近最低固有频率时，这会对容器壁面和容器结构带来严重的不利影响。对于液舱晃荡的研究，主要集中在液舱所受的最大晃荡冲击载荷以及液舱晃荡受力与时间之间的关系及其统计特征。

在早期受计算手段的限制，研究液舱晃荡问题都是用试验的方法来模拟和记录的，但从70年代开始，CFD技术的发展和兴起，很多有效的数值计算方法得以实现，开始用数值手段来进行晃荡问题的模拟求解。有限元法、有限差分方法等被应用于晃荡问题的求解中。通过很多研究者的计算模拟，发

现对晃荡问题模拟的最关键的问题在对自由液面变化的精确捕捉。在整个模拟的时间过程中，自由液面的形状和运动实时发生变化，同时由于壁面边界也在做运动，相应的液体在发生迁移，这造成了自由液面运动的强非线性特征，大大增加模拟仿真的难度。近年来，无网格方法逐渐兴起，表现出有限元法和有限差分法等所不具备的优势［1］。FPM是无网格方法中很重要的一种，在计算流体中有着很好的适应性，对于解决自由液面大变形问题有其独特之处。

在前人研究液舱晃荡理论的成果中，给出不同浸深比下晃荡的共振频率与液舱形状和大小之间的关系。对于二维简化的矩形液舱，其共振频率公式可表述如下:

式中: fn为频率; a为液舱内的水深; b为液舱内水的宽度; n为拟合的阶数，其中一般情况都只按一阶情况来处理即可; g为重力加速度。通过计算得到的二维液舱共振频率，来制定进行数值计算模拟时所采用的舱壁摇荡频率。

1　FPM计算概述

FPM (Finite Point Method )是由Onate和Idelsohn等［2－3］于1996年提出的。FPM采用了移动最小二乘法(MLS)生成形函数，是不用预先生成网格作为背景的方法，利用配点法生成离散粒子点，将代数方程进行离散求解，在计算流体力学领域中的应用有独特的优势。

FPM离散和近似的目的是为了求解流体力学控制方程［4］，控制方程包括质量守恒方程、动量守恒方程和能量守恒方程。其中离散和近似的方法简要介绍如下。

1.1配点法

FPM使用配点法来对空间场量进行离散，根据几何模型特征来确定所计算的流体域，在流体域内产生计算节点进行离散。由于计算流体域可能随时间而变化，因此定义某时刻的计算流体域为Ω( t)，边界为Ω( t)。在计算域生成一系列的计算粒子点集，其中将计算粒子点进一步划分为计算域内部的粒子点集，计算域边界粒子点集。

离散得到的每个粒子点都携带相应位置处的场量信息，粒子点的位置信息随着时间实时发生变化。

1.2移动最小二乘法(MLS)

分析流体域Ω中场变量u(x)，在x处u(x)的MLS近似表达式为

式中p(x)为对于2维空间坐标xT=［x，y］的基函数。为保证基函数p(x)的最小完备性，采用Pascal三角形求解。式(2)中的a(x)为一系数向量，可表示为

注意，式(3)中的系数向量a(x)是x函数。系数a(x)可进行加权离散取极小得到

式中: n为包含在权函数珚W(x－xi)≠0的x支持域中的计算节点数; ui为u在x = xi处的计算点物理量。式(4)是一种泛函形式，主要是针对场函数的加权残量，用粒子点坐标参数和近似函数来得到场函数的近似形式。对泛函进行求导如下:

导数为0的点即为驻点，可得到对空间场量分布的最佳近似。

1.3自由液面处理

在本文计算中，自由液面是FPM所需解决的主要问题。在FPM中，自由液面通过自由边界粒子来描述，在每个时间步长开始时，都需要进行遍历检测自由面粒子点。在自由边界上，表面张力占很大的比重，在压力张量和表面张力张量之间存在着力的平衡。

τ·n= kκn。(6)

式中:τ为压力张量; k为表面张力;κ为自由面曲率。压力张量可以分解为压力部分和衰减的压力张量部分，后者可以进一步表示为对称的速度变形张量，具体表示形式如下:

将式(7)乘以nT，得到压力和速度的耦合方程为:

自由面粒子的速度－时间方程为

对式(9)需要补充不可压缩条件·u = 0。通过上述自由液面粒子点运动方程即可对自由液面粒子点的运动进行求解，使用粒子点对自由液面波形进行精细化模拟。

2　二维液舱晃荡计算模型

二维矩形舱模型如图1所示。计算结果与Yang C［5］所得结果做比较。对液舱舱壁采用水平激励，约束舱的运动，实现水平振荡运动，其运动方程可表述为

x= Asin(ωt)，

式中: x为水平位移; A为振幅;ω为圆频率，ω= 2π/T，T为周期［6］。

图1　液舱晃荡计算模型Fig.1　Computational model of sloshing tank

用式(10)来计算该液舱一阶近似的共振周期

在计算中，取振幅A为0.05 m。在共振周期周围取13个周期进行计算，具体周期见表1，图2中的计算图像都是计算周期内容。在观测整个晃荡过程中，壁面所受的横向力Fx时间历程，和观测点处波高时间历程，计算真实时间为20个周期，计算图像如图2所示。将12个工况下的结果进行统计分析，得到每个工况下的最大横向力和最大波高。此外，还取周期为1.265 s的工况，以验证共振周期(见图3)。

3　计算图像分析

从计算所得到的图像可以看出，随着周期的改变，其液面形状也发生很大的改变，其中周期越大，所具有的完整波形就越少。由于图片截取时刻的差异，在图中波形存在不同。从总体上看，随着周期的增长，波长幅值也在增大。

图2　不同周期的计算图像Fig.2　Image in different period

图3　共振周期t = 1.265 sFig.3　Image in resonant period t = 1.265 s

此外，通过图3的的测量证实，本二维矩形舱的共振周期为1.265 s，在此周期下，液舱内共有4个完整波形。

4　计算结果分析

4.1激励周期校对

由于在计算液舱晃荡时，壁面运动与兴波传递存在着一定的时间差。为了确定这个时间差，特选取如图1中所示近壁面的A处作为测量点，测量不同时刻的波高和横向力，通过波高的变化周期来得到内部流场的周期。A是相对测量点，与两侧壁面保持固定位置，随着液舱的晃动而运动，不对内部流场产生影响。

表1　给定周期与测量周期对比Tab.1 The comparison of given and measured period

从表1可看出，在计算过程中，预设周期与计算中实测周期相差很微小，保证了液面波形周期的可知性。从而也说明，FPM计算方法对边界的运动和内流场激励的实时性，数值延迟和失真现象几乎可以忽略不计。

4.2最大横向力与周期

为了更清晰地表征舱壁所受最大的横向力与晃荡激励周期之间的变化关系，先将两者分别进行无因次化处理，如图4所示。其中Tn为共振周期;ρ= 1 000 kg/m3; g= 9.8 m/s2; l= 1 m; b= 0.35 m。

图4　最大横向力与周期的曲线对比图Fig.4 The comparison on the curves of maximum force with period

从图4可看出，FPM方法计算结果与试验结果之间差异。大体上看，两者走势相同，其中当最大横向力超过峰值后，随着周期的增大，FPM理论计算值与试验值之间的差异变得越来越小，误差控制在10%以内。这表明FPM对于边界所受力的计算合理可信，并未受自由液面变形的影响使计算误差增大。

4.3最大波高与周期

同样将最大波高与周期进行无因次化处理，L为液舱的宽度，Tn为共振周期。

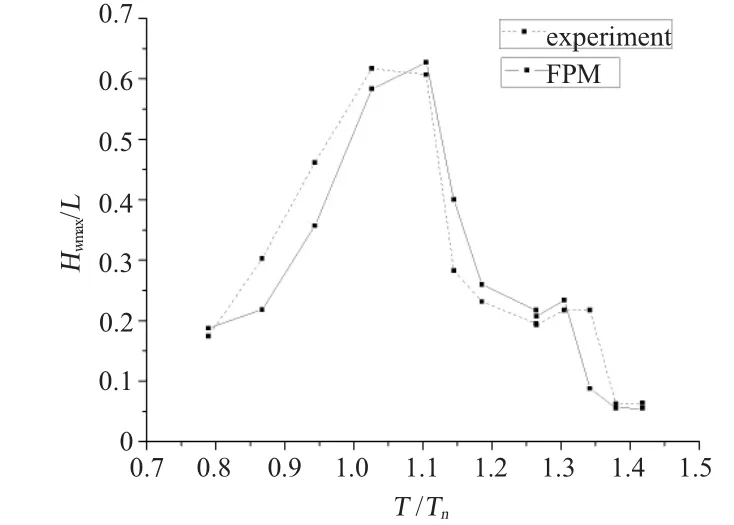
图5　最大波高与周期的曲线对比图Fig.5 The comparison on the curves of maximum wave height with period

从图5可看出，对于最大波高的测量，FPM数值计算值与试验值的变化趋势相同，在数值大小上存在一定差异，在周期较大的情况，误差相对较小。两者之间最大的不同在于峰值的不同，一方面是因为本图采用折线图，使得最大值的捕捉存在误差，另一方面是在FPM计算中，是采用粒子点的位置来判断波高位置，由于粒子点数目的限制，对于最高值的定位也就产生了不同。

5　结语

本文利用FPM在液舱晃荡模拟过程中，其主要难点在于对剧烈变化的自由液面和动边界进行模拟。通过上述计算分析，可得出如下结论:

1)通过监视A处的变化周期，证实了在FPM中边界运动与内部流体粒子点运动相互作用的实时性;同时从计算图像上可以看出，边界例子点与内部流体粒子点没有发生干涉、分离等现象，自由液面形状捕捉良好;

2)在液舱舱壁运动的激励下，液舱内的液体也随之发生迁移运动，液面也在不断的变化波形，并且波形的变化周期并不是与晃荡周期相同，呈现处强烈的非线性特征;从计算数据上看，FPM对于动边界所受砰击力及液体波高的计算误差较小，适用于液舱晃荡关键问题的计算和模拟。

参考文献:

［1］张雄，刘岩．无网格法［M］．北京:清华大学出版社，2004: 137－210．

［2］ONATE E，IDELSOHN S，ZIENKIEWICZ O C，et al．A finite point method in computational mechanics．Applications to convective Transport and fluid flow［J］．Int．J．Numer．Methods Engrg，1996，39:3839－3866．

［3］ONATE E，IDELSOHN S，ZIENKIEWICZ O C，et al．A stbilized finite point method for analysis of fluid mechanics problems［J］．Comp．Meth．Appl．Mech．Eng．，1996，139: 315－346．

［4］王福军．计算流体动力学分析［M］．北京:清华大学出版社，2011:4－12．

［5］YANG C，LOHNER R．Computation of 3D flows with violent free surface motion［C］/ /Proceeding of the 15th ISOPE，Seoul，Korea．June，2005:19－24．

［6］祁江涛，顾民，吴乘胜．液舱晃荡的数值模拟［J］．船舶力学，2008，15(8) :574－581．

［7］TIWARI S，KUHNERT J．Finite pointset method based on the projection method for simulations of the incompressible Navier-Stockes equations［J］．Springer LNCSE: Meshfree methods for Partial Differential Equations，Vol．26，Ed by M．Griebel，M．A．Schweitzer，2002．

［8］KUHNERT J．An upwind finite pointset method for compressible Euler and Navier-Stokes equations［J］．Springer Lecture Notes in Computational Science and Engineering: Meshfree Methods for Partial Differential Equations I，2002．

［9］LUO Yun-hua，ULRICH H C．A generalized finite difference method based on minmimizing global residual［J］．Comput．Methods Appl．Mech．Engrg，2002，191:1421－1438．

［10］LIU G R，LIU M B．Smoothed particle hydro-dynamics: a meshfree particle methods［M］．World Scientific，2003．

作者简介:郑亚雄(1990－)，男，硕士，助理工程师，研究方向为船舶水动力学。

基金项目:航空科学基金资助项目(20122305003)

收稿日期:2014－06－27;修回日期: 2014－09－09

文章编号:1672－7649(2015) 07－0034－04doi:10.3404/j.issn.1672－7649.2015.07.008

中图分类号:U661．32

文献标识码:A