多源网络编码数据完整性验证方案

牛淑芬,王彩芬,张玉磊,曹素珍

(西北师范大学计算机科学与工程学院,兰州730070)

多源网络编码数据完整性验证方案

牛淑芬,王彩芬,张玉磊,曹素珍

(西北师范大学计算机科学与工程学院,兰州730070)

基于同态向量哈希函数和向量合并算法,提出一种能够抵御污染攻击的多源网络编码数据完整性验证方案。通过信源节点计算发送向量的哈希值,利用私钥对该哈希值进行签名,并将消息向量、哈希值以及哈希值的签名发送至中间节点。中间节点和信宿节点基于系统公钥,验证来自不同信源节点的线性编码消息的完整性。实验结果表明,当信源节点数大于200时,该方案的计算效率优于现有多源网络编码方案,更适用于大规模分布式网络数据的安全验证。

多源网络编码;数据完整性;聚合签名;同态哈希函数;向量合并算法;离散对数问题

1 概述

Ahlswede和Cai等人［1］于2000年提出网络编码理论,网络编码允许网络中间节点在传统数据转发的基础上参与数据处理,已成为提高网络吞吐量、鲁棒性和安全性的有效方法,但网络编码易遭受系统污染攻击,一旦网络中的某个信息被某蓄意节点恶意篡改,或在传输过程中由于外界原因发生变异,该污染信息将在整个网络中迅速繁殖,使目的节点无法恢复源信息,导致网络传输失败。在密码学中,通常用基于同态哈希函数的签名［2］和同态数字签名技术［3］解决线性网络编码中的污染问题。利用签名函数或者同态哈希函数的同态性,中间(信宿)节点用公钥验证数据的真实性。文献［4］系统地讨论了线性网络编码的安全问题,提出一个层次式抵御污染攻击的安全协议,该协议能够实现污染节点的具体定位。

然而,现有算法大多是针对单源网络编码设计,而在多源网络编码中,该问题就会变得复杂,主要原因在于:现有单源网络编码签名算法只需一个私钥对消息进行签名,而在多源网络编码中,这个唯一的私钥显然不能被多用户共享,且用不同的私钥签名

会破坏现有某些算法中的签名同态性。针对多源网络编码,学者们提出了一系列签名算法。文献［5］利用签名函数同态性提出一个安全的签名算法,该方案每个源节点用自己的私钥签名,中间节点用每个源节点的公钥验证,该方案的缺点是每个信源节点要计算一组签名,计算量相对大。文献［6］提出一个安全高效的多源网络编码签名算法来预防网络中的污染攻击,并讨论了算法的安全性。文献［7］提出一个有效抵抗污染攻击的多源网络编码签名算法,但不足之处在于仅能供信宿节点进行验证。文献［8］给出一个针对多源网络编码的数字签名,对于来自不同信源节点(不同子空间)的向量,提出向量合并算法,设计一个多源网络编码的签名体制,并给出算法安全模型定义。文献［9］为多源网络编码构建一个无条件安全的认证码技术,保证消息的完整性。文献［10］提出一个在标准模型下可证明安全的签名算法。从以上文献可以看出,虽然学者们对多源网络编码的签名算法做了很多研究,但都存在较多的局限性。

本文基于文献［8］提出的向量合并算法,利用文献［11］的同态哈希函数构建一个数据完整性验证方案。每个信源节点首先计算消息的向量哈希值,然后用BGL聚合签名算法［12］对哈希值进行签名。中间(信宿)无需知道信源节点的私钥即可验证收到消息的完整性。该方案的安全性取决于向量哈希函数和BGL聚合签名的安全性。

2 相关知识

2.1 双线性映射

设q是一个大素数,G1,G2是2个有着相同素数阶q的乘法循环群,g是G1的生成元。假设在群G1,G2中的离散对数问题是难解的。一个双线性映射e:G1×G1→G2在G1上满足下列性质:

(1)双线性:对任意的a,b∈Zq、g,h∈G1,存在e(ga,hb)=e(g,h)ab。

(2)非退化性:存在a,b∈Zq,使得e(ga,gb)≠1。(3)可计算性:对所有的g,h∈G1,存在有效算法计算e(g,h)。

2.2 困难问题假设

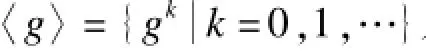
定义2(Diffie-Hellman(DH)问题) 设G1是阶为q的循环群,g是G1的生成元,已知g,gα,h∈G1,计算hα。

2.3 同态向量哈希函数

定义3(向量哈希函数) 设G是一个阶为p的循环群,随机选择公共参数g1,g2,…,gd∈G,则向量v=(v1,v2,…,vd)∈Zp的哈希函数为:

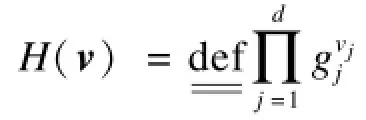
容易证明,向量哈希函数满足以下性质:

(1)同态性:对任意2个向量m1,m2和2个实数w1,w2,满足H(w1m1+w2m2)=H(m1)w1H(m2)w2。

(2)免碰撞性:不存在一个多项式时间的攻击者伪造一个向量m3,同时满足m3≠w1m1+w2m2且H(m3)=H(m1)w1H(m2)w2。

定理1 同态向量哈希函数在离散对数问题是困难问题假设下是安全的［11］。

2.4 多源线性网络编码

随机线性网络编码的随机性体现在网络编码的局部编码系数是有限域内的随机数,线性表示网络编码节点的输入和输出之间的关系是线性的［13］。多源网络用一个无环有向图G=(V,E)来表示,其中,E为网络中链路的集合;V为网络中所有节点的集合［14］。网络中有l个信源节点S=(s1,s2,…,sl)⊂V向网络中另一个节点集合T⊂V中的所有信宿节点传输消息,其中,每个源节点都独立地传输消息,且不知道任何其他节点的传输行为［15］。信源节点在传输前对它要发送的信息进行分块处理,把要发送的文件分成m个分块,每个分块用一个n(n≥m)维的行向量来表示,行向量的元素为有限域内的数据,文件可以表示为向量v=(v1,v2,…,vn)。每个信源节点在发送消息前,先对消息进行如下预处理:

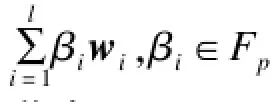
3 多源网络编码的数据完整性验证

本文方案能够组合来自不同信源节点的向量,同时也能够利用公钥对来自不同私钥签名的消息进行验证,所以,在基于同态向量哈希函数的基础上,本文方案利用聚合签名和向量合并算法［8］。

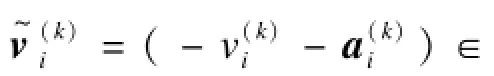
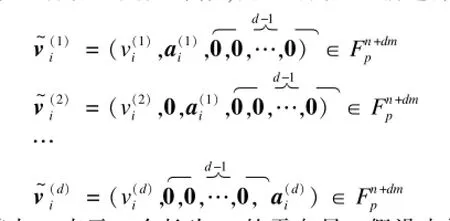
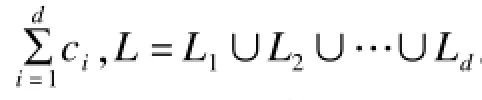
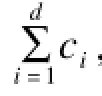
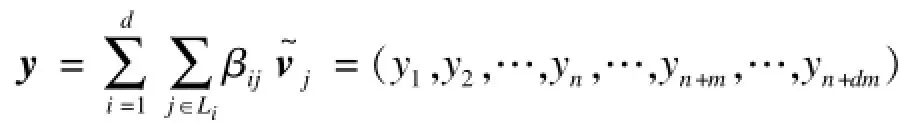
计算出βij=yn+(i-1)m+j,即可以计算出组合的编码系数。

在本文验证方案中有三方:信源节点,中间节点和信宿节点。完整性验证技术由5个算法组成: Setup,KeyGen,Sign,Combine,Verifying。记NS= (Setup,KeyGen,Sign,Combine,Verifying),算法具体描述如下:

(1)Setup:给定安全参数1k:

1)产生一个四元对(G1,G2,GT,e),其中,G1,G2,GT是阶为素数p的3个循环群,e:G1×G2→GT为一个有效的双线性映射。随机产生gi←G1{1} (i=1,2,…,n)和g←G2{1}。

2)H1:{0,1}∗→G1是一个哈希函数。

(2)KeyGen:源节点Si随机选择xi∈Zp,计算pi=gxi。源节点的公私钥对为(pi,xi)。

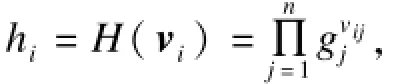
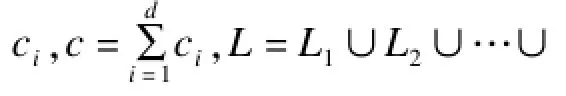
(5)Verify:给定消息向量,向量的哈希值hi以及向量的签名σi,y∈Fp:

2)如果以下2式均成立:

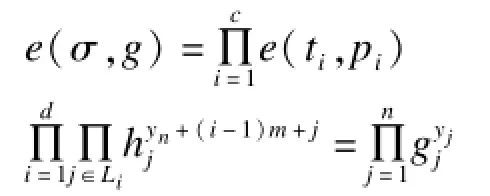
则输出0(接受),否则输出1(拒绝)。

正确性证明:

(1)验证消息哈希值:

(2)验证数据完整性:

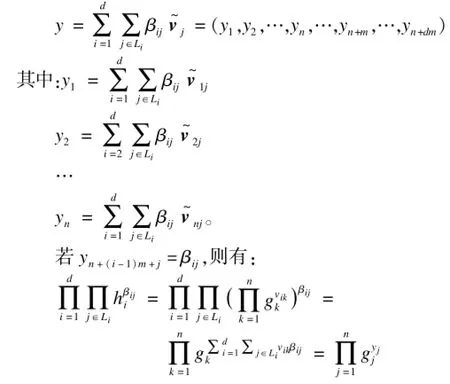
4 安全性分析

在本文算法中,无需一个安全通道来发送每个向量的哈希值,哈希值的正确性通过聚合签名算法验证,而数据完整性通过向量哈希函数性质来验证。

定理2数据完整性验证算法NS是安全的,假设哈希函数VH和聚合签名算法BGL是安全的。特别地,假设存在一个多项式时间的攻击者A攻破NS算法,则存在一个多项式时间攻击者B对BGL算法伪造一个签名以及存在一个多项式时间攻击者C能攻破向量哈希算法VH,使得:

其中,NS_Adv［A,NS］是攻击者A攻破算法NS的概率。

4.1 签名伪造

数据完整性是通过同态哈希函数验证的,中间

4.2 哈希碰撞

攻击者对给定的哈希值伪造一个消息使其通过验证,即攻击者选定一个消息,攻击想伪造一个哈希值h()使得对已知消息w≠及其哈希值h(w),有h(w)=h()。由定理1可知,对任何一个攻击者来说,伪造一个消息向量使其通过验证相当于求解离散对数问题。

由以上分析可知,在本文方案中,在计算性Diffie-Hellman困难问题假设下,攻击者不可能伪造消息向量的哈希值;在离散对数困难问题假设下,攻击者不可能伪造一个向量使其通过验证。

5 实验结果与分析

从理论上分析本文方案在验证阶段计算开销方面的优势,给出具体数值结果。在所有表及图中:d表示信源节点的个数;n表示消息向量的唯数;c表示中间节点编码的消息向量的个数。

5.1 计算开销

本节比较本文方案与文献［3,7］方案在计算开销方面的执行效率,Cme表示执行一次指数运算花费的时间,Cpar表示执行一次对运算花费的时间,Cmul表示执行一次乘法运算花费的时间,MSP表示算法支持多源网络编码。为简单起见忽略所有计算负担轻的加法运算。假设验证者收到c个来自不同源节点的消息向量,按照多源线性网络编码理论:n≥d,n≥candd≥c。

表1表明本文方案需要执行对运算时间与文献［7］方案相同,但执行乘法和指数运算的时间优于文献［7］方案。

表1 验证阶段的计算开销

5.2 实验结果

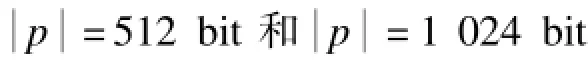
表2 对参数的主要性质

5.2.1 运行效率

本文分别运行了在不同对参数下信源节点签名与中间或者信宿节点验证的时间。对每一个信源节点来说,签名时间主要决定于消息向量的大小。在这种情况下,可信源节点个数为d=50,消息向量维数分别为n=10,50,150,200,在2种对参数Type a和Type e下分别运行信源节点签名与中间或者信宿节点验证的时间。对每一个验证节点(中间节点或者信宿节点)来说,验证的计算效率主要取决于文件的个数和消息向量的大小。因此,本文假设消息向量的长度为3 200 Byte,同时消息向量的个数分别设为10,50,100,200,300。

算法签名阶段和验证阶段的运行时间分别如图1、图2所示,可以看出,对固定的对参数,算法运行时间随着消息向量大小的增加而增加。在对参数Type a下,当信源节点的个数为200时,算法运行时间为1 500 ms。

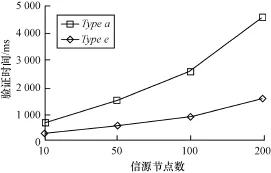
图1 验证时间比较

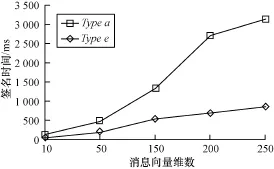
图2 签名时间比较

5.2.2 分析比较

从数据实验角度比较本文方案与文献［7］方案在验证阶段的计算效率。本文选择对参数类型为Type a,向量维数为50。由表3可以看出,当信源节点个数d＞200时,本文方案运行时间优于文献［7］方案。

表3 算法运行时间比较s

6 结束语

本文提出一个多源网络编码数据完整性验证方案,利用向量合并算法计算来自不同信源节点的向量的线性组合,其作用是能够计算出线性编码系数。方案的数据完整性由同态向量哈希函数验证,哈希函数的正确性通过聚合签名算法进行验证。通过理论分析和数据测试结果表明,本文方案是可行有效的,具有良好的扩展性。随着全同态密码算法研究的深入,今后将设计基于全同态密码函数的多源网络编码签名算法,进一步提高算法的安全性及数据完整性验证的效率。

［1]Ahlswede R,CaiN,LiSYR,etal.Network Information Flow［J］.IEEE Transactions on Information Theory,2000,46(4):1204-1216.

［2]Gkantsidis C,Rodriguez P.Cooperative Security for Network Coding File Distribution［C］//Proceedings of the 25th IEEE International Conference on Computer Communications.Washington D.C.,USA:IEEE Press, 2006:1-13.

［3]Boneh D,Freeman D,Katz J,et al.Signing a Linear Subspace:Signature Schemes for Network Coding［C］// Proceedingsof2009ConferenceonPublicKey Cryptography.Berlin,Germany:Springer,2009:68-87.

［4]Adeli M,Liu H.On the Inherent Security of Linear Network Coding［J］.Communications Letters,2013, 17(8):1668-1671.

［5]罗 蛟.安全多源网络编码环签名方案［EB/OL］.(2012-04-12).http://www.paper.edu.cn.

［6]彭 勇,陈愈强,严文杰.一种安全的多源网络编码签名算法［J］.计算机工程与应用,2012,48(30): 135-139.

［7]Vajda I.SignaturesforMulti-sourceNetwork Coding［EB/OL］.(2010-06-04).http://eprint.iacr.org/2010/328.

［8]Agrawal S,Boneh D,Boyen X,et al.Preventing Pollution AttacksinMulti-sourceNetworkCoding［C］// Proceedingsof2010ConferenceonPublicKey Cryptography.Berlin,Germany:Springer,2010:161-176.

［9]Yang H,Yang M.An Unconditionally Secure Authentication CodeForMulti-sourceNetworkCoding［J］.InternationalJournalofWirelessandMicrowave Technologies,2012,2(1):45-49.

［10]Shao Jun,Zhang Jinlin,Ling Yun,et al.Multiple Sources Network Coding Signature in the Standard Model［M］// Pathan M,Wei Guiyi,Fortino G.Internet and Distributed Computing Systems.Berlin,Germany:Springer,2013: 195-208.

［11]Krohn M N,Freedman M J,Mazieres D.On-the-fly Verification of Rateless Erasure Codes for Efficient ContentDistribution［C］//ProceedingsofIEEE Symposium on Security and Privacy.Oakland,USA: IEEE Press,2004:226-240.

［12]Boneh D,Gentry C,Lynn B,et al.Aggregate and VerifiablyEncryptedSignaturesfromBilinear Maps［C］//Proceedings of EUROCRYPT’03.Berlin, Germany:Springer-Verlag,2003:416-432.

［13]牛淑芬,王彩芬.多源线性网络编码的同态签名算法［J］.计算机工程,2012,38(2):126-128.

［14]牛淑芬,王彩芬,刘雪艳.抵御污染攻击的双源网络编码签名算法［J］.计算机应用,2011,31(6):1512-1514.

［15]严文杰.网络编码签名算法［D］.武汉:武汉理工大学,2010.

［16]The Pairing-basedCryptographyLibrary［EB/OL］.(2010-07-15).http://crypto.stanford.edu/pbc/.

编辑 陆燕菲

Data Integrity Verification Scheme for Multi-source Network Coding

NIU Shufen,WANG Caifen,ZHANG Yulei,CAO Suzhen
(College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,China)

Taking advantage of vector merging algorithm and homomorphic Hash function,this paper proposes a data integrity scheme for multi-source network coding against pollution attacks.Each source node computes raw massage’s Hash values and uses a secure mechanism to sign the Hash values,then appends the Hash values and its signatures to each message which sends to forward nodes and sink nodes.The forwarder can verify the integrity of network coded data from different source nodes without knowing the sources private keys and generating the Hash for the combined messages.Experimental results show that the computation efficiency of the proposed scheme is better than the existing multi-source network coding scheme,and it is more suitable for the large-scale distributed network data security verification.

multi-source network coding;data integrity;aggregate signature;homomorphic Hash function;vector merging algorithm;discrete logarithm problem

牛淑芬,王彩芬,张玉磊,等.多源网络编码数据完整性验证方案［J］.计算机工程,2015,41(3):21-25.

英文引用格式:Niu Shufen,Wang Caifen,Zhang Yulei,et al.Data Integrity Verification Scheme for Multi-source Network Coding［J］.Computer Engineering,2015,41(3):21-25.

1000-3428(2015)03-0021-05

:A

:TP309.7

10.3969/j.issn.1000-3428.2015.03.004

国家自然科学基金资助项目(61163038);西北师范大学青年教师科研提升计划基金资助项目(NWNU-LKQN-13-12)。

牛淑芬(1976-),女,副教授、博士,主研方向:网络编码,云计算,无线传感器网络;王彩芬,教授、博士生导师;张玉磊,副教授;曹素珍,副教授、硕士。

2014-04-01

:2014-06-03E-mail:sfniu76@nwnu.edu.cn