基于MAS模型检测与抽象的Web服务验证

许兴旺,骆翔宇,2

(1.华侨大学计算机科学与技术学院,福建厦门361021;2.桂林电子科技大学广西可信软件重点实验室,广西桂林541004)

基于MAS模型检测与抽象的Web服务验证

许兴旺1,骆翔宇1,2

(1.华侨大学计算机科学与技术学院,福建厦门361021;2.桂林电子科技大学广西可信软件重点实验室,广西桂林541004)

Web服务组合现已成为跨组织业务流程集成的关键技术,然而在松耦合开发模式和开放的互联网运行环境下,其正确性、可靠性、安全性等可信性质难以得到保证。为解决该问题,提出一种Web服务组合形式化验证方法,将基于图状反例向导的抽象与精化方法应用于多主体系统(MAS)模型检测工具(MCTK)中,大幅缓解模型检测的状态爆炸问题,从理论上证明该验证方法的正确性。实验通过将银行贷款风险评估系统转换成MCTK描述的MAS,并对比抽象前后的模型检测代价,结果显示,基于抽象的Web服务验证方法明显优于未采用抽象技术的验证方法。

Web服务组合;多主体系统;模型检测;图状反例;抽象;精化

1 概述

面向Web服务的软件开发已成为跨组织业务流程集成的关键技术。然而,单一Web服务功能有限,在多数情况下不能满足用户需求,因此出现将多个Web服务按某种特定组合集成为一个面向不同需求用户且有统一接口服务的技术。由于服务及其协同的动态性,开放多变的互联网运行环境以及松耦合的服务开发模式导致开发和运行过程不确定,使得服务的正确性、可靠性、安全性、可用性、时效性等可信性质难以得到保证［1］。

目前,研究者主要应用模型检测［2］的方法来验证服务组合的上述性质。如文献［3］用模型检测器SPIN自动分析提取来自BPEL的、扩展有限状态自

动机EFA转化的、Promela语言描述的程序的方法,文献［4］用UPPAAL分析验证WS-CDL和WSBPEL并且自动将其转化为的有序时间状态机的方法,文献［5］给出利用自主研发的模型检测工具WSAT进行验证的方法。但上述验证方法均不支持验证服务组合的时态认知性质。为此,文献［6-7］将Web服务组合描述成多主体系统(Multi-Agent System,MAS),并用模型检测器MCMAS验证了其计算树逻辑(Computation Tree Logic,CTL)性质和认知性质。文献［1］将BPEL描述的Web服务组合流程转换为模型检测器MCTK的输入语言描述的多主体系统,并验证了Web服务组合的时态认知性质。文献［9］提出将Web服务组合转换成MCMAS的输入语言描述的多主体系统,并验证了其时态认知性质。文献［8］把Web服务分别转换为MCTK描述的多主体系统和MCMAS描述的多主体系统,并用这2种工具分别验证时态认知性质,通过对比验证所花代价证明了MCTK的性能优于MCMAS。

然而,上述方法均未采用优化技术来缓解模型检测的状态爆炸问题。由于Web服务组合的状态空间巨大,因此本文采用能有效缓解状态爆炸问题的抽象方法［10］,并基于模型检测多主体系统验证Web服务组合的CTL性质和时态认知性质。

2 基本概念

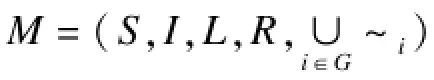
其中,Δi表示各Δ在i上的分量;Δ代表S,R或I。对于全局状态s和s′,定义s～is′⇔si=s′i,容易证明这是一个等价关系。给定一个抽象函数h和上述定义的Kripke结构M,M关于h的抽象模型定义为,满足:

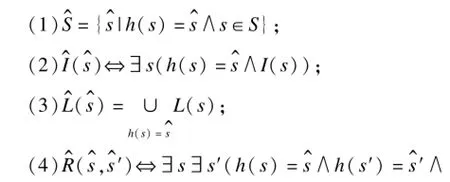
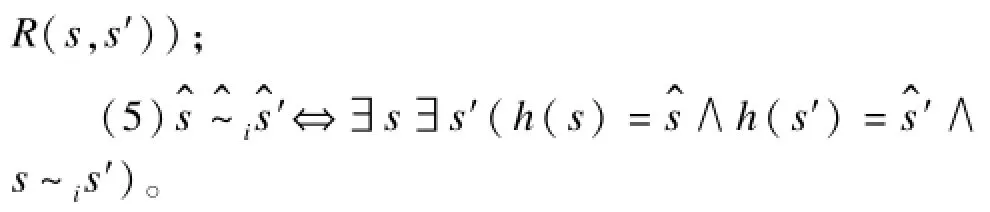
将所需验证的逻辑统一用CTLK(Computation Tree of Logic and Knowledge)表示,其意义语法和语义可在文献［13］中查询,为便于本文有关定理证明,仅给出个体知识Kiφ,普遍知识EGφ和公共知识CGφ的语义,其中,φ是任意ECTLK公式。

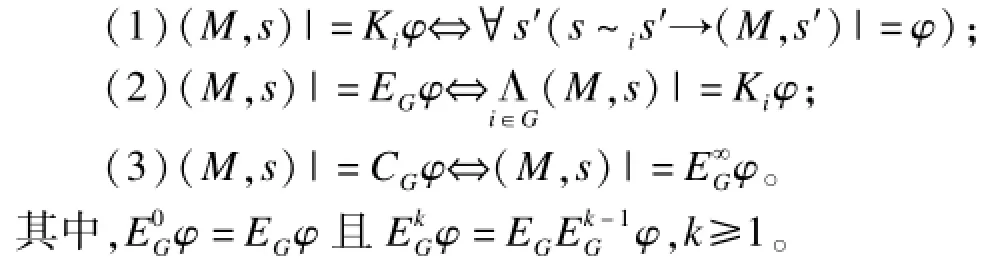
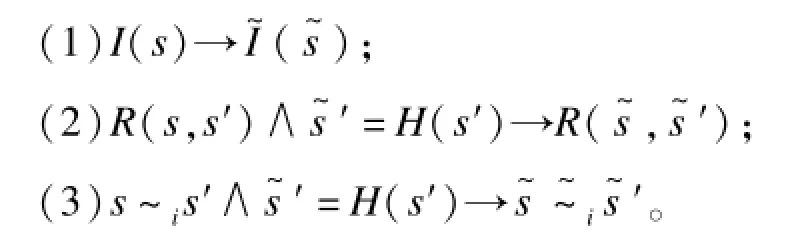
如果将抽象函数看成一个模拟函数,从抽象模型的定义来看,抽象模型和原始模型的关系满足以上偏序模拟关系的每个条件,从而可以得出抽象函数就是抽象模型和原始模型间的偏序模拟关系。

定理1设,h是一个抽象函数,则对于任意ACTLK公式φ,有。

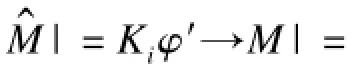
3 时态认知逻辑的图状反例

为给出图状反例,考虑一个简单的认知逻辑公式Kiφ,其中,φ是一个纯时态公式。从个体知识的定义可知(M,s)|≠Kiφ⇔∃s′(s～is′∧(M,s′)|=φ)。因此,存在一个主体i在状态s下的可能世界s′(如果s～is′成立,s′是主体i在s下的可能到达世

界),s′是纯时态公式¬φ的证据。在已有文献中,纯时态公式的反例和证据都是一个线性路径,因此,这条证据也是一条线性路径。在模型检测中,对于任一公式θ,有M|=Kiφ⇔∀s0(I(s0)→(M,s′)|=φ)。

图1是Kiφ的一个图状反例示意图。其中,φ是纯时态公式;圆圈表示状态;标记i的虚线表明对于主体i来说,虚线两端的状态互为对方的认知可达状态;s0和s0′都是初始状态;箭头表示状态迁移;省略号表示一条由若干状态构成的线性路径(可以是空的状态序列)。这个反例由认知和时态路径两部分组成,最外层的时态路径部分为s0′→…→s1→…,认知部分由状态s0,s1以及它们之间的虚线构成,把这种反例称为时态认知逻辑公式的图状反例。

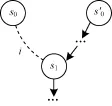
图1 Kiφ的图状反例

定义时态认知逻辑公式的反例的图状结构为D=(EP,linki(s,s′),T),其中:

(1)T反例最外层的一条时态路径称为反例的时态部分,它或者是一条有限的路径,或者是一条尾端带环的无限路径。

(2)EP=空集|图状反例,称为认知部分。

(3)linki(s,s′)表示认知部分(如果不为空)最外层的一个状态s和T中的一个状态s′具有认知可达关系s～is′,其中,i是出现在公式最外层的主体。

如果公式是纯时态公式,则EP为空,反例为一条时态路径,即说明纯时态公式的反例也是图状的反例,因为纯时态公式也是时态认知公式。

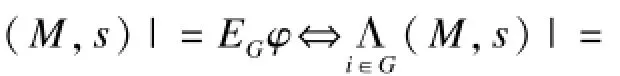
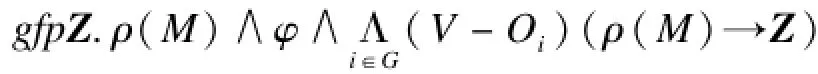
4 图状反例向导的抽象与精化

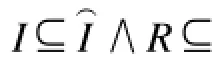
由定理1的证明和上文讨论得到定理2。由于篇幅所限,证明过程省略。

定理2如果状态空间相同的模型与M有以下近似关系,则对于任意ACTLK公式φ,有。

4.1 初始抽象系统的生成

在实际抽象中,计算抽象系统的近似系统(简称近似抽象系统),从定理1和定理2可以推知,如果一个ACTLK公式在近似抽象系统中成立,则其一定在原始系统中成立。然而,这个断言的否命题和逆命题却不成立,因此,在实际抽象中,把这个近似抽象系统叫做初始抽象系统,在后续中还将根据实际情况对其进行精化。

采用文献［11］中提及的近似技术,文献［11］证明了该近似技术能保证近似系统的条件,即如果是通过这种近似技术得到的模型,是原始模型的抽象模型,则有,从而有。

将初始状态集合I、迁移关系集合R看成是定义在系统变量集合V={vi|1≤i≤n}上的n元谓词。设h为抽象函数,其定义为:

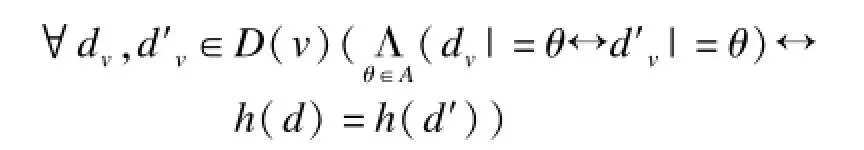
转换函数A将V上的任意n元谓词P转换成上的n元谓词函数。其中,是近似抽象系统的系统变量集合,只不过其定义域为。转换函数定义如下:

(1)如果P是原子谓词,则:

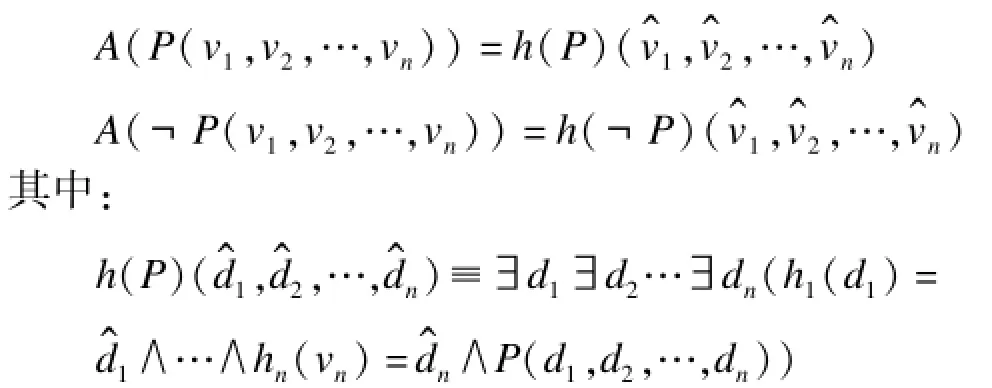
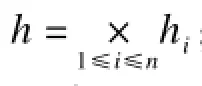
(2)如果P=P1∧P2,则A(P)=A(P1)∧A(P2);

(3)如果P=P1∨P2,则A(P)=A(P1)∨A(P2);

(4)如果P=∀vP′,则A(P)=∀v^A(P′);

(5)如果P=∃vP′,则A(P)=∃v^A(P′)。

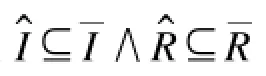
在实际中,抽象是针对自主研发的多主体系统模型检测工具MCTK的输入语言的抽象。MCTK在对输入语言描述的系统作模型检测时,以二元决策图(Binary Decision Diagram,BDD)表示其从输入文件中抽取的初始状态集合和迁移关系集合。把这2个集合分别用ℑ和ℜ表示,利用BDD运算A,计算出抽象模型状态空间、A(ℑ)和A(ℜ),即得到一个近似抽象系统。因为MCTK是符号化模型检测器,所以使用BDD作上述运算。

根据文献［11］对这种初始抽象系统生成方法做了一些改进,具体如下:因为输入语言的程序中包含对系统迁移条件的描述,以及待验证性质的描述,并且迁移条件由原子命题的布尔运算构成,验证的性质在布尔运算基础上又加了时态算子和认知算子,所以,从输入语言程序中可以抽取出一个原子命题集合。令A表示这个集合。将A作以下划分,以FC=×jFCj表示这个划分,函数F:A→FC表示划分函数。划分原则为:∀θ1,θ2∈A(F(θ1)=F(θ2)↔var(θ1)∩var(θ2)≠Φ),其中,var(θ)表示出现在原子命题θ中的变量集合。

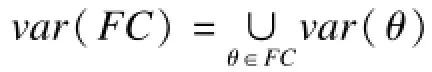
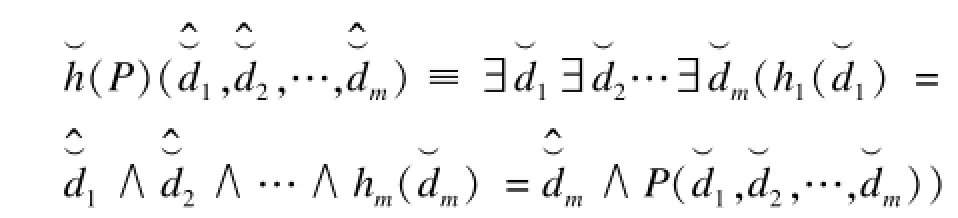
4.2 图状反例向导的精化

如上文叙述,在初始抽象系统中不成立的性质在原始系统中不一定不成立。这种情况下模型检测给出的反例称为伪反例。对于纯时态逻辑公式,其原因及消除伪反例的方法在文献［11］中已经叙述。

对于时态认知公式,通过图2举例说明。假设待验证的公式是Ki(y＜2),抽象后,待验证的公式为。图2中原始系统的可达状态只有图2中所示的3个初始状态。各图形符号的含义与图1中相同,状态中标明的系统变量在状态中取值。原始系统左边2个状态被抽象为初始抽象系统左边的状态。

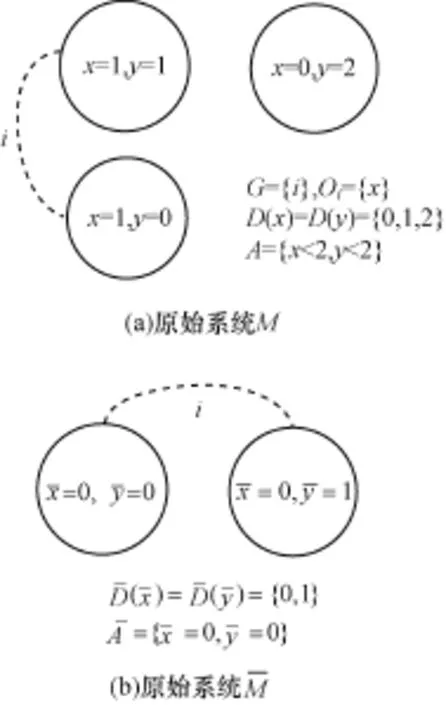
图2 初始抽象实例

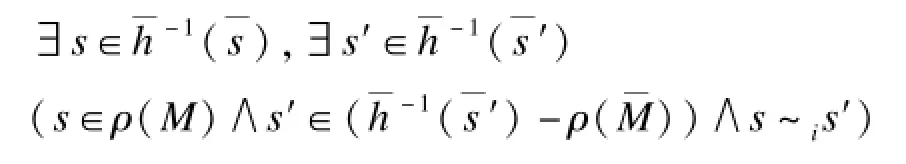
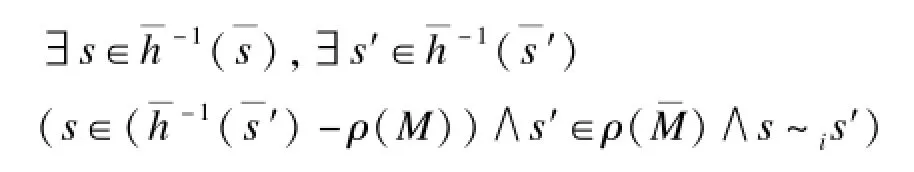
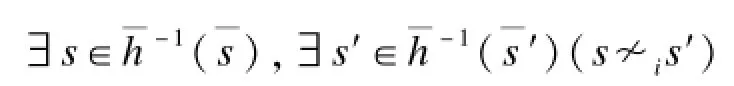
因为对于时态部分的精化与文献［11］中的精化相同,通过简单推理可以证明其可以把上文中前2个原因消除,所以本文的精化只考虑第(3)个原因。消除这个原因叫做消除伪认知,与伪反例时态部分相对应。

消除伪反例的前提是确定反例就是伪反例,即识别伪反例。纯时态公式的伪反例的识别及消除在文献［11］中已有详述,并且图状伪反例时态部分的识别和消除与其基本一致,因此本文仅考虑消除伪认识。

在下文识别伪反例算法splitCounterexample中,将splitSequence表示识别时态部分,如果反例不是伪反例,则splitSequence返回一个反例,否则返回一个失败状态集,返回结果可参见文献［11］。

算法1splitCounterexample Algorithm

其中第19行的K(S,i)表示主体i在状态集合S中所有可能世界的集合,如果时态部分是伪时态,则第2行返回一个失败状态集,如果认知部分是伪认知,则第20行返回2个失败状态集,否则返回一个图状反例。下文是识别认知部分反例的算法。

算法2splitEP Algorithm

算法3PolyRefineEpistemic Algorithm

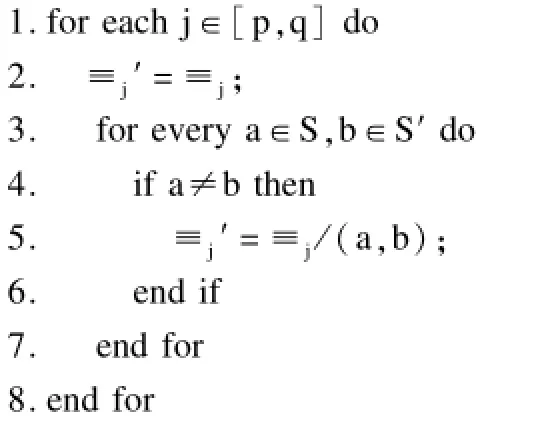
5 Web服务组合的验证

在现有基于多主体系统模型检测来验证Web服务组合的方法中,通常是通过某种手段把Web服务组合转化为一种多主体系统的形式化模型,然后将这种模型通过模型检测器的输入语言输入到模型

检测器中,并在输入文件中人工加入需要验证的Web服务组合的性质,最后执行模型检测,模型检测返回的验证结果即为验证服务组合的结果。

文献［1,8］分析了BPEL所描述的Web服务组合业务流程和WSDL所描述的各服务接口,把BPEL语法结构转换成一种中间结构迁移七元组,然后将这种迁移七元组转换成多主体系统的Kripke结构,最后使用MCTK验证这个多主体系统。

采用上述基于转换的建模方法,结合本文提出的图状反例向导的抽象与精化,构成本文验证方法。通过改进MCTK,使其能够生成本文的图状反例,并能够运行下文中的机械算法。算法中包含的Web服务组合到多主体系统的转换算法已在文献［1,8］中实现,并且由4.1节可以容易得出抽象算法,所以不再详述这些算法,用transAlgorithm和Abstract Algorithm分别表示转换和抽象算法,RefineAlgorithm表示将时态部分精化算法和算法3整合后得到的算法。假设不论splitCounterexample返回几个失败集,返回结果都将输入RefineAlgorithm由其进行精化。由于算法是机械的,且篇幅有限,因此用自然语言描述该验证算法。

算法4Verification Algorithm

Verification(Composition)//Composition是待验证Web服务组合

(1)运行transAlgorithm(Composition)将Composition转化为SMV描述的多主体系统MAS并在其中加入待验证的性质φ;

(2)MCTK读入多主体系统描述模型,运行Abstract Algorithm(MAS)获得初始抽象系统MASabs;

(3)运行模型检测算法,如果φ成立,则退出算法,否则转入步骤(4);

(4)对模型检测返回的反例,运行伪反例识别算法IdentAlgorithm(),如果不是伪反例,则退出算法,否则转入步骤(5);

(5)运行RefineAlgorithm,得到一个精化后的抽象系统,转入步骤(3)。

6 实验结果与分析

以一个银行贷款风险评估系统为实验对象。系统中贷款申请客户端是一个服务组合接口,货款申请者通过这一接口向组合内银行提供的Web服务申请贷款,当贷款额小于10 000元时,这个Web服务向风险评估Web服务请求评估风险,否则向评估专家Web服务请求评估风险。当评估结果低时银行接受贷款请求,否则银行拒绝贷款。设置系统中可以受理的贷款额范围分别为9 000元～11 000元和5 000元～15 000元并分别进行实验。实验平台为:Intel Pentium 4处理器,主频3.00 GHz;1 GB内存;Ubuntu 12.04操作系统;模型检测工具MCTK-1.0.1。实验结果如表1所示。

表1 MCTK模拟银行贷款风险评估系统实验结果

从表1可以看出,不管贷款金额的范围有多大,采用抽象技术的验证时间都为0.023 s,并且远小于未采用抽象技术的验证时间,表明本文采用抽象技术的服务组合验证比不采用抽象技术的服务验证性能更优。

7 结束语

在研究现有基于多主体模型检测验证Web服务组合的基础上,本文提出采用抽象技术的验证方法,该抽象方法是一种图状反例向导的抽象与精化方法,实验结果表明其在很大程度上缓解了基于多主体模型检测的Web服务组合验证中的状态爆炸问题,性能明显优于不采用优化技术的验证方法。本文抽象方法与Clarke反例向导的抽象［11］类似,不同的是本文提出时态认知逻辑的图状反例以及此类反例向导的抽象,并且解决了多主体系统的抽象,而Clarke的方法只支持传统有限状态系统抽象。与Lomuscio抽象方法［12］相比,本文采用的多主体系统的Kripke结构较Lomuscio采用的解释系统形式化程度更高,因此抽象效果更好。

由于大多数Web服务组合方案有实时性建模和验证需求,因此今后将在本文研究的基础上进一步研究多主体实时系统的模型检测和抽象方法,并将其应用于Web服务组合的实时性验证。

［1]骆翔宇,谭 征,苏开乐,等.一种基于认知模型检测的Web服务组合验证方法［J］.计算机学报,2011, 34(6):1041-1061.

［2]Clarke E M,Peled D G.Model Checking［M］.Boston, USA:MIT Press,1999.

［3]Nakajima S.Model-checking Behavioral Specification of BPEL Applications［C］//Proceedings of WCE’06.Washington D.C.,USA:IEEE Press,2006:89-105.

［4]Diaz G,Pardo J J,Cambronero M E,et al.Automatic TranslationofWs-cdlChoreographiestoTimed Automata［M］//Bravetti M,Kloul L,Zavattaro G.Formal Techniques for Computer Systems and Business Processes.Berlin,Germany:Springer,2005:230-242.［5]Fu Xiang,Bultan T,Su Jianwen.Analysis of Interacting BPEL Web Services［C］//Proceedings of the 13th InternationalConferenceonWorldWideWeb.New York,USA:ACM Press,2004:621-630.

［6]Lomuscio A,Solanki M.Towards an Agent Based Approach for Verification of OWL-S Process Models［M］// Aroyo L,Traverso P,Ciravegna F,et al.The Semantic Web:ResearchandApplications.Berlin,Germany: Springer,2009:578-592.

［7]Lomuscio A,Qu H,Solanki M.Towards Verifying Compliance in Agent-based WebServiceCompositions［C］//Proceedings of the 7th International Joint Conference onAutonomousAgentsandMultiagent Systems.Washington D.C.,USA:IEEE Press,2008: 265-272.

［8]骆翔宇,陈 艳.Web服务的形式化验证［J］.计算机工程,2010,36(5):257-259.

［9]骆翔宇,王 昆,王凤钗.一种Web服务组合的认知模型检测方法［J］.小型微型计算机系统,2011,32(12): 2041-2047.

［10]Clarke E M,Grumberg O,Long D E.Model Checking and Abstraction［J］.ACM Transactions on Programming Languages and Systems,1994,16(5):1512-1542.

［11]Clarke E,Grumberg O,Jha S,et al.Counterexampleguided Abstraction Refinement for Symbolic Model Checking［J］.Journal of the ACM,2003,50(5): 752-794.

［12]Cohen M,Dam M,Lomuscio A,et al.Abstraction in Model Checking Multi-agent Systems［C］//Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems.New York,USA:ACM Press,2009:945-952.

［13]Su K,Sattar A,Luo X.Model Checking Temporal Logics of Knowledge Via OBDDs［J］.The Computer Journal,2007,50(4):403-420.

编辑 陆燕菲

Verification of Web Services Based on MAS Model Checking and Abstraction

XU Xingwang1,LUO Xiangyu1,2
(1.College of Computer Science&Technology,Huaqiao University,Xiamen 361021,China;
2.Guangxi Key Laboratory of Trusted Software,Guilin University of Electronic Technology,Guilin 541004,China)

Web services composition is a key technology to solve cross-organizational business process integrations.However,it is hard to ensure its trusted properties(including correctness,reliability,safety),because of the loosely coupled development paradigm and open Internet running environment.To solve this problem,this paper proposes a formal verification and abstraction method for Web services composition based on model checking Multi-Agent Systems (MAS)and refinement.By applying the method of the graph-like counterexample guided abstraction and refinement on MCTK,it greatly reduces the state explosion problem of model checking.The correctness of the method is proved theoretically.Recording to the experimental results of which translates a credit risk assessment Web services to a MAS programmed by input language of MCTK then model checks both abstracted and un-abstracted MAS,the Web services verification based on proposed method works much more efficiently than the normal verification based on MAS model checking.

Web services composition;Multi-Agent System(MAS);model checking;graph-like counterexample; abstraction;refinement

许兴旺,骆翔宇.基于MAS模型检测与抽象的Web服务验证［J］.计算机工程,2015,41(3):26-31,36.

英文引用格式:Xu Xingwang,Luo Xiangyu.Verification of Web Services Based on MAS Model Checking and Abstraction［J］.Computer Engineering,2015,41(3):26-31,36.

1000-3428(2015)03-0026-06

:A

:TP311

10.3969/j.issn.1000-3428.2015.03.005

国家自然科学基金资助面上项目(61170028);华侨大学中青年教师科研提升计划基金资助项目(ZQN-YX109);华侨大学高层次人才科研启动基金资助项目(11BS108);广西可信软件重点实验室基金资助项目(kx201323)。

许兴旺(1989-),男,硕士,主研方向:Web服务组合,模型检测技术;骆翔宇(通讯作者),副教授。

2014-02-28

:2014-04-25E-mail:decemberxf@163.com