基于距离补偿模型的改进DV-Hop定位算法

高文根,陈其工,江 明,李云飞,牛明强

(安徽工程大学检测技术与节能装置安徽省重点实验室,安徽芜湖241000)

基于距离补偿模型的改进DV-Hop定位算法

高文根,陈其工,江 明,李云飞,牛明强

(安徽工程大学检测技术与节能装置安徽省重点实验室,安徽芜湖241000)

传统的DV-Hop定位算法在估计网络平均跳距时,采用锚节点之间的物理直线距离代替信号实际传播距离,两者之间存在的距离误差会引起平均跳距估计不精确,从而导致较高的节点定位误差。针对该问题,提出一种改进算法。分析物理直线距离和实际传播距离存在误差的原因,将其总结为节点随机布置导致的节点间距离不均匀,以及实际传播路径与物理直线距离的偏离,并根据不均匀度和偏离度建立距离补偿模型,使物理直线距离更接近实际传播距离。与传统算法相比,改进算法未增加算法复杂度和额外的硬件设备。仿真结果表明,该算法较好地补偿了锚节点之间的距离,显著提高了算法对于未知节点的定位精度。

距离补偿;估计距离;不均匀度;偏离度;DV-Hop定位算法;无线传感器网络

1 概述

目前,无线传感器网络(Wireless Sensor Network, WSN)已经广泛应用于诸多领域,如自然环境的监测、远程医疗监控等［1］。在这些应用中,远程控制端所接收到的数据,只有在具备显示数据或者事件发生地点的条件下,才能作为有效地信息,帮助远程控制端或者人类实现相应的控制或者检测目的,没有携带发生位置的信息,没有实用性［2-3］。因此,对无线传感器网络来说,节点的位置信息是至关重要的。

在现有的无线传感网络定位算法中,主要存在2类定位算法,其主要区别在于,如何获得节点之间

的距离信息。由此,主要可以分成基于测距和无需测距(Range-Free)的2类定位算法。基于距离的定位算法常用测距方法有RSSI(Received Signal Strength Indicator),TOA(Time of Arrival),TDOA (TimeDifferenceonArrival),AOA(Angleof Arrival),且定位精度相对较高,同样要求节点硬件达到一定的条件。无需测距的定位算法不依赖节点之间的据对距离和方位,在成本上,更加适用于大规模的网络。基于无需测距的定位算法主要有质心算法、DV-Hop算法、APIT算法、MDS-Map算法等［4］,其中DV-Hop算法应用较为广泛。

文献［5］给出的改进DV-Hop算法,在采用改进PSO算法的基础上,对WSN的部署覆盖进行了优化。文献［6］算法通过Max-Min方法和多个参考节点的改进方式,来提高定位的精度。文献［7］在原算法的基础上,提出了修正距离误差的算法,降低节点定位误差。针对原DV-Hop算法由于平均跳距带来的估计距离误差,本文建立了数学模型,对距离误差进行估计,修正未知节点到锚节点的估计距离,以期提高定位精度。

2 DV-Hop定位算法

DV-Hop定位算法由美国路特格斯大学(Rutgers University)的Niculescu等人［8］提出。该算法主要由3个阶段组成［9-10］:第1阶段,完成节点间信息的交换,锚节点将信息传递至除自己外的所有节点,使之获得与锚节点的跳数;第2阶段,网络平均跳距的估计和传播。网络中锚节点在获得其他锚节点的相应信息后,计算网络平均每跳距离,然后将其作为校正值广播至网络中。所有网络节点只记录接收到的第一个校正值,并通过邻居节点转发,接着根据记录的最小跳数,计算到附近各个锚节点的跳段距离;第3阶段,完成坐标定位。最后当未知节点获得与3个或更多锚节点间的距离时,采用数学方法计算自身坐标。

3 DV-Hop算法的改进

3.1 DV-Hop定位算法问题描述

在传统DV-Hop算法中,平均跳距的估计是基于锚节点之间的物理直线距离。如图1所示,锚节点i的平均跳距的获得如下:

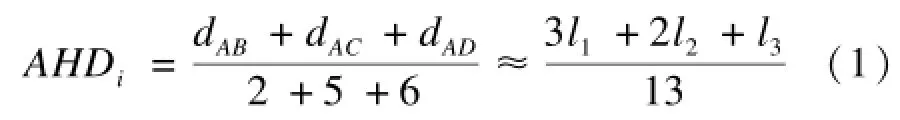
假设未知节点获得的校正值来自锚节点i,那么:

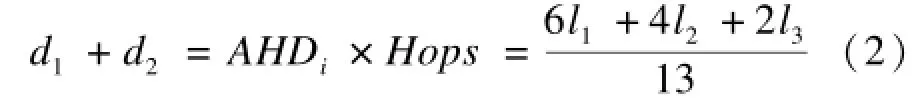
假设l2＞l1＞l3＞R,有:

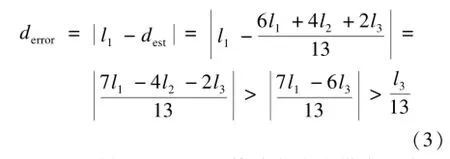
显然,这样的平均跳距估计方式会带来很大的定位误差。

图1 传统DV-Hop算法的网络拓扑结构

3.2 距离补偿模型

如图1所示,锚节点i和j之间的物理直线距离,与实际传播距离的误差,主要由未知节点1部署的随机性,使得实际传播路径偏离了锚节点i和j物理直线所在路径,导致实际传播距离和物理直线距离之间产生距离误差。

要实现节点A和C之间的通信,节点B必须部署在2个节点A和C的重叠通信区域部分,显然,节点B偏离度最大时,即节点B处在如图2所示的位置。

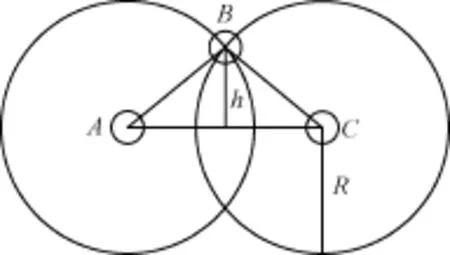
图2 网络拓扑的偏离度示意图

此时,如果节点A和C相互靠近,即dAC不断减少,直到临界条件:dAC=R。此时,偏离度h达到最大值:

节点A,B,C所在的区域节点密度为:

如果增加节点A和C之间的传输节点,即局部节点密度增加,如图3所示。

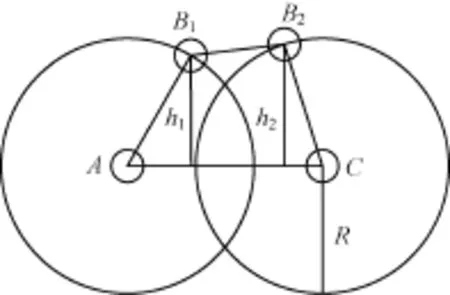
图3 节点密度增加部分网络拓扑的偏离度示意图

在中间传输节点个数增多的条件下,节点B1,B2的偏离度明显大于节点B的偏离度,即在节点密度增加一定程度时,会影响到偏离度的大小。A,B1,B2,C所在区域的节点密度为:

此节点密度的下限临界值如式(5)所示,上限临界值为:

如果局部节点密度超过此界限,由于传播路径的可能性增多,在一定程度上会降低偏离度。同时,偏离度服从均匀分布［11］,则有:

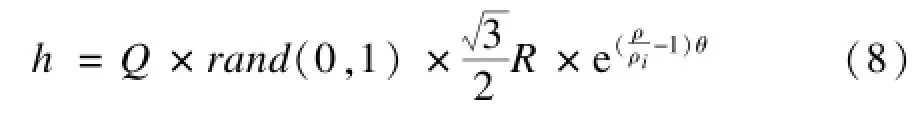
将图1中的不均匀度消除后,所形成的节点的拓扑结构如图4所示。显然,即使在没有偏离度的条件下,由于节点分布的不均匀性,同样会带来节点之间距离的不均匀性,从而导致节点定位误差。

图4 偏离度为0的网络拓扑结构

假设网络中相邻节点之间的距离均为R,那么相邻节点之间不均匀度为0,如图5所示。

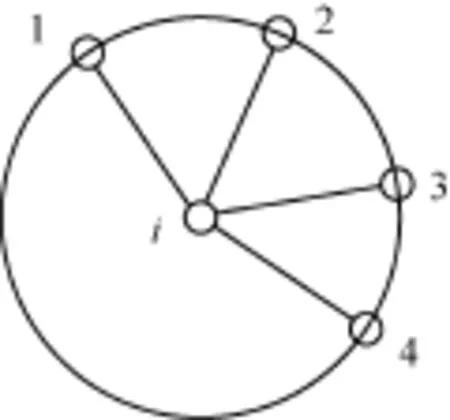
图5 不均匀度为0的网络拓扑结构

可以得出此时的节点密度为:

其中,n是节点周围的节点个数。在最理想的条件下,不均匀度为0所对应的最大节点个数为:

最大的节点密度和最小密度为:

在理想情况下,节点密度不超出［ρmin,ρmax］,节点的不均匀度为0。在实际情况下,节点的不均匀度受到节点部署影响［12-13］,因此,节点不均匀度呈现自然指数变化。

如图1所示,未知节点1的不均匀度为:

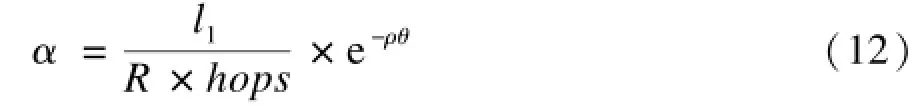
同时,有:

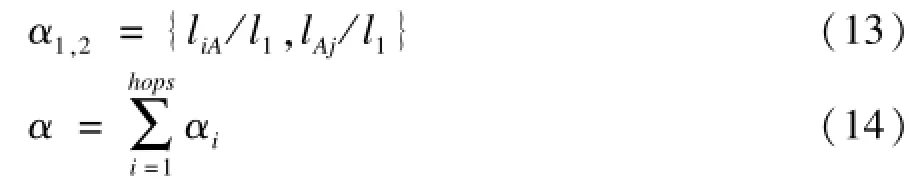
由此,可以得到:

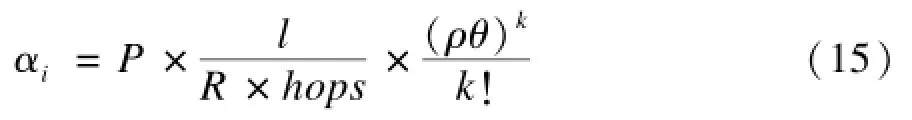
其中,i,k=1,2,…,hops。

基于以上结论,本文提出以下距离补偿公式:

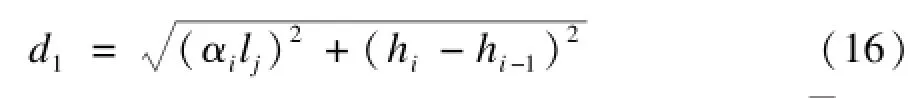
4 算法仿真及分析

为了检验算法的性能,在MatLab中同时对本文提出的改进定位算法、文献［11］提出的改进定位算法、原DV-Hop定位算法3种算法进行仿真,并对所出现的仿真结果进行评估和分析。网络中所有节点都随机分布在特定的区域(100 m×100 m)。3种算法性能的评估,都是基于相同条件下,呈现不同锚节点密度、节点通信半径对不同算法的性能影响。每种性能的仿真基于100次仿真结果的平均值。WSN随机部署节点分布图如图6所示,其中,圆形表示未知节点;星形表示锚节点,锚节点比例为10%。

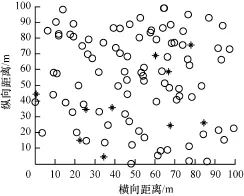
图6 WSN随机部署节点分布

定义节点定位误差δ为:

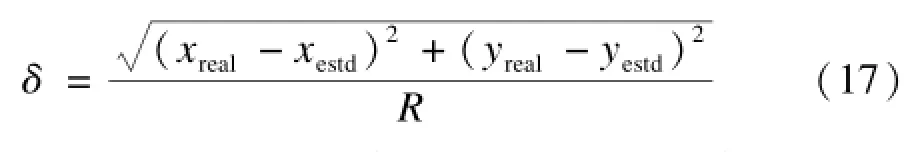
其中,(xreal,yreal)是未知节点实际的坐标;(xestd,yestd)是估计出来的未知节点的坐标;R表示节点的通信半径。节点平均定位误差为已定位为未知节点的误差和与能被定位的未知节点个数比值。

仿真结果如图7～图9所示,本文提出的改进定位算法记为改进DV-Hop1,文献［11］提出的改进定位算法记为改进DV-Hop2,原DV-Hop定位算法记为DV-Hop。

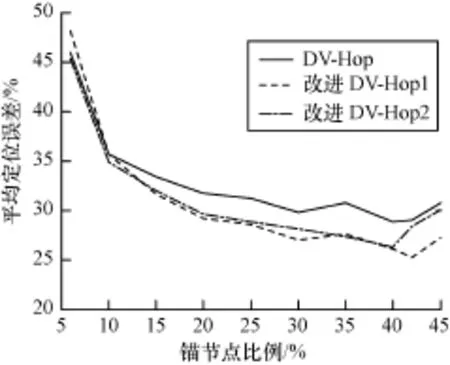
图7 平均定位误差随锚节点个数的变化曲线

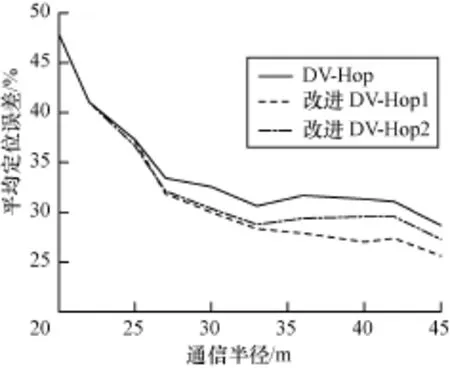
图8 平均定位误差随节点通信半径的变化曲线

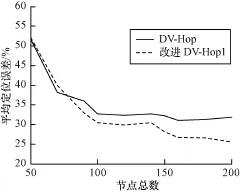
图9 平均定位误差随节点总数的变化曲线

图7显示,随着锚节点比例的增大,DV-Hop、改进DV-Hop1和改进DV-Hop2都逐渐下降,改进算法的变化趋势与原算法保持一致,且误差率一直要低于原算法。改进算法在锚节点比例较少时,优化程度较低,锚节点个数较少,在距离补偿的过程中,对平均跳距的影响较小,不能很大程度地降低节点定位误差,因此,3种定位算法误差率相当。随着锚节点比例的增大,2种改进算法的性能逐渐优于原算法,改进DV-Hop1稍优于DV-Hop2。当锚节点比例很大时,改进DV-Hop1在对更多锚节点进行距离补偿后,更加有效地调节平均跳距,明显地降低定位误差。虽然锚节点比例增大有利于提高改进DV-Hop2的有效性,但由于没有考虑节点之间的不均匀度,造成了在锚节点比例很大时,反而降低了模型的有效性,相对提高了误差。

图8显示,当通信半径较小时,改进DV-Hop1的误差率与原算法、改进DV-Hop2的误差率基本接近。随着通信半径的增大,改进DV-Hop1的误差率明显低于原算法、改进DV-Hop2的误差率。当节点的通信半径较小时,锚节点之间的跳数相对增多,在部署区域不变的条件下,式(9)中局部节点密度相对变大,虽然能提高偏离度的估计精度,但局部节点密度的变化,使得不均匀度精度受到较大影响,使改进算法的距离补偿精度降低。随着通信半径的增大,节点间跳数相对减少,偏离度和不均匀度有效地补偿了锚节点间距离,另一方面,式(9)中节点密度相对变小,而在整体节点密度不变的条件下,通信半径的变化有效地提高了不均匀度的估计精度,从而提高了节点的定位精度。

图9显示,在监测区域随机部署不同数量的节点,数量为50,75,…,200,每个节点的半径均为30 m,同时,每次部署的节点中,锚节点比例保持30%不变。在节点密度不断增大的趋势下,改进算法和原算法的定位误差率都呈现递减趋势。在节点密度较低时,锚节点数量较少,对于距离补偿模型对平均跳距的修正作用较小,因此,节点定位误差率较高。随着节点密度增大,锚节点相应数据的增多,都使得距离补偿模型很好地修正了平均跳距,有效性有很大程度提高,有效地降低了节点定位误差率。但当节点密度很大时,误差率降低趋势变缓。说明节点分布密度过大,对节点定位并不一定会有很好的效果。

5 结束语

本文在分析传统DV-Hop算法缺陷的基础上,提出一种基于距离补偿模型的改进DV-Hop定位算法。该算法在不增加额外硬件设备和算法复杂度条件下,能有效补偿原算法中锚节点之间距离的不足,在保持原算法简单、低成本优点的前提下,较好地降低定位误差。在改进算法中,随着锚节点比例和通信半径的变化,优化算法对锚节点间距离的修正程度愈发明显,这也从侧面反映出所提出的理论模型的可行性和有效性,但在锚节点比例和通信半径都较大的条件下,模型没有做出预测,同时,仿真结果也说明,还可以在锚节点稀疏和稀疏网络的情况下做进一步的研究。

［1]孙利民,李建中,陈 瑜.无线传感网络［M］.北京:清华大学出版社,2005.

［2]Yick J,Mukherjee B,Ghosal D.Wireless Sensor Network Survey［J］.Computer Networks,2008,52(12):2292-2230.

［3]Karl H,Willig A.Protocols and Architectures for Wireless Sensor Networks［M］.［S.l.］:Wiley,2005.

［4]Niculescu D.Positioning in Ad Hoc Sensor Networks［J］.IEEE Network,2004,18(4):24-29.

［5]朱海荣,李 平,陈 剑.基于改进PSO算法的WSN覆盖优化方法［J］.计算机工程,2011,37(8):82-85.

［6]Dai Ying,Wang Jianping,Zhang Chongwei.Improvement of DV-Hop Localization Algorithms for Wireless Sensor Networks［J］.Wireless Communications Networking and Mobile Computing,2010,1(4):23-25.

［7]Yi Xiao,Liu Yu,Deng Lu,et al.An Improved DV-Hop Positioning Algorithm with Modified Distance Error for Wireless Sensor Network［C］//Proceedings of the 2nd International Symposium on Knowledge Acquisition and Modeling.Washington D.C.,USA:IEEE Press,2009: 216-218.

［8]Niculesca D,Nath B.DV Based Positioning in Ad Hoc Networks［J］.Journal of Telecommunication System, 2003,22(14):267-280.

［9]Wang Ruijin,Zhang Bo,Shen Yang,et al.PHDV-Hop: A More Accurate DV-Hop Positioning Algorithm in WSN［J］.International Journal of Digital Content Technology and Its Applications,2012,6(13):89-97.

［10]Kumar S,Lobiyal D K.An Advanced DV-Hop Localization Algorithm for Wireless Sensor Networks［J］.Wireless Personal Communications,2013,71(2):1365-1385.

［11]李云飞,江 明,娄 柯,等.无线传感器网络中DVHop定位算法的改进［J］.计算机工程与应用,2014, 50(3):79-81.

［12]唐 弢.基于锚节点的无线传感器网络定位技术研究［D］.哈尔滨:哈尔滨工业大学,2013.

［13]李旭东,赵 雪.矩形和椭圆内均匀分布随机点定理及应用［J］.成都理工大学学报,2012,39(5): 555-558.

编辑 金胡考

Improved DV-Hop Localization Algorithm Based on Distance Compensation Model

GAO Wengen,CHEN Qigong,JIANG Ming,LI Yunfei,NIU Mingqiang
(Anhui Key Laboratory of Detection Technology and Energy Saving Devices,Anhui Polytechnic University,Wuhu 241000,China)

The traditional DV-Hop localization algorithm estimates the average hop distance with the physical distance between the anchor nodes instead of actual transmission distance,and the distance error between the two kinds of distance undoubtedly leads to the inaccuracy of the average hop distance and relatively high localization error.Aiming at this problem,the improved algorithm is proposed.The reason of error between the physical distance and actual transmission distance is analyzed in the paper,and is summarized as the asymmetry of distance resulted from the nodes random distribution,as well as the deviation degree between the actual transmission path and the physical distance,and the distance compensation model is built based on the asymmetry and deviation degree to make the physical distance closer to the transmission distance.The improved algorithm increases no extra hardware and the complexity of the DV-Hop.The simulation results show that the improved algorithm compensates the distance between the anchor nodes,and improves the localization accuracy to the unknown nodes.

distance compensation;estimated distance;asymmetry degree;deviation degree;DV-Hop positioning algorithm;Wireless Sensor Network(WSN)

高文根,陈其工,江 明,等.基于距离补偿模型的改进DV-Hop定位算法［J］.计算机工程,2015, 41(3):32-36.

英文引用格式:Gao Wengen,Chen Qigong,Jiang Ming,et al.Improved DV-Hop Localization Algorithm Based on Distance Compensation Model［J］.Computer Engineering,2015,41(3):32-36.

1000-3428(2015)03-0032-05

:A

:TP393

10.3969/j.issn.1000-3428.2015.03.006

国家自然科学基金资助项目(61271377,61172131)。

高文根(1973-),男,讲师、博士研究生,主研方向:无线传感器网络;陈其工(通讯作者),教授、博士生导师;江 明,教授;李云飞、牛明强,硕士研究生。

2014-10-08

:2014-11-04E-mail:ahpuchina@ahpu.edu.cn