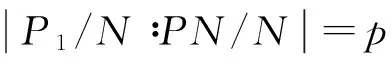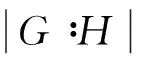关于F-反正规的极大子群与s-完备
2015-02-10高胜哲
高 辉, 高胜哲, 尹 丽
(大连海洋大学 理学院 辽宁 大连 116023)
关于F-反正规的极大子群与s-完备
高 辉, 高胜哲, 尹 丽
(大连海洋大学 理学院 辽宁 大连 116023)
设F是包含所有超可解群类的饱和群系,利用F-反正规的极大子群的s-完备性来刻画群的结构,得到了群G∈F的一些充要条件.
群系;F-反正规的极大子群; 正规指数;s-完备
0 引言
设F是一个群类, 称F是一个群系, 若满足(1)G∈F且H◁G, 则G/H∈F; (2)G/H∈F且G/K∈F, 则G/(H∩K)∈F. 称群系F是饱和的, 如果G/Φ(G)∈F,可推出G∈F.
设F是包含所有超可解群类的饱和群系,GF是使G/N∈F的所有正规子群N的交.文[1-3]分别通过GF的极小子群和GF的Sylow子群的极大子群来刻画G∈F.文[4]提出了F-正规的概念.文[5]利用了F-反正规的完备性刻画了群的结构.设F是包含U的饱和群系,有限群G∈F当且仅当对于每个F-反正规且有合数指数的极大子群M, 存在一个关于M的极大完备C,使得G=MC且C/K(C)的阶无平方因子.文[6]利用了极大θ-完备获得超可解群的一个刻画.有限群G超可解当且仅当对于有合数指数的极大子群M,M有一个极大θ-完备C, 使CG/K(C)循环.
但是, 注意到以往的研究分别是通过对完备和θ-完备赋予“极大”这一条件来刻画群的结构. 为了得到更好的结论, 对赋予的“极大”这一条件去掉, 文[7]中给出了极大子群的s-完备这一概念.本文借助F-反正规的极大子群的s-完备的条件, 得到了G∈F的一些充要条件.
本文中所用符号皆为标准的, 涉及的群指有限群,S和U分别表示所有可解群类和所有超可解群类.
1 定义及引理
定义1[4]设M是G的极大子群, 若G/MG∈F, 称M在G中F-正规.否则,称M在G中F-反正规.
显然地,G∈F当且仅当G的所有的极大子群在G中F-正规.
定义2[8]设M是G的极大子群.G的一个子群C称为M在G中的一个完备, 如果CM,而C的每个G-不变真子群都在M中. 用K(C)表示C的所有G-不变真子群之积, 则K(C) 定义3[7]给定群G的极大子群M, 设C是关于M的完备,称C是关于M的s-完备, 如果C=G或者存在G的子群B,使得(i)C是B的极大子群;(ii)B不是关于M的完备. 定义4[9]给了群G及极大子群M, 令N/K是G的一个主因子,满足G=MN,并且N有尽可能小的阶,N/K的阶叫作M在G中的正规指数,记作η(G∶M). 定义5定义下列集合. 引理1[5]每个极大子群M在G中F-反正规,当且仅当G=GFM. 引理2[7]令G是一个群,N◁G使得G/N有唯一极小正规子群U/N, 设M是群G的极大子群,满足N≤M但UM. 令F是一个子群闭的同态像, 假设C是M的s-完备, 且有C/K(C)∈F, 但U/N∉F. 记则是M的s-完备,且满足:且).是的极大子群. 引理3Φ1(G)可解. 证明假设命题不真, 设G为极小阶反例. 若F1(G)=∅, 则∀M<·G,均有η(G∶M)无平方因子, 从而G超可解, 于是Φ1(G)=G超可解, 矛盾. 故F1(G)≠∅且设Φ1(G)≠1, 则G非单. 令N是G的极小正规子群, 由G的极小性知,Φ1(G/N)可解, 又Φ1(G)N/N≤Φ1(G/N), 故Φ1(G)N/N可解. 若N∩Φ1(G)=1, 则Φ1(G)可解, 矛盾. 于是N∩Φ1(G)≠1, 即N≤Φ1(G), 从而Φ1(G)/N可解, 且N是G的唯一极小正规子群. 引理4[9]群G超可解,当且仅当对于G的每个有合数指数的极大子群M,η(G∶M)无平方因子. 引理5[10]设F是包含U的饱和群系, 假设群G有素数阶正规子群N,使得G/N∈F, 则G∈F. 引理6设F是包含U的饱和群系,群G∈F,当且仅当G的每个F-反正规的极大子群M,有η(G∶M)无平方因子. 证明必要性证明.若G∈F, 则G的每个极大子群是F-正规, 所以必要性显然成立. 充分性证明.假设结论不成立且设G为反例. 若GF=G, 假设存在M<·G使得M在G中F-正规, 则GF≤M. 于是G≤M, 矛盾. 所以∀M<·G,M均在G中F-反正规, 由题设知,η(G∶M)无平方因子. 由引理4知,G超可解. 特别地,G∈F, 矛盾. 引理7[11]设F是包含U的饱和群系, 假设G有正规子群E使得G/E∈F, 若E为循环群, 则G∈F. 引理8[7]令F是一个群系, 假设群G∉F, 那么存在一个正规子群N,使得G/N∈b(F), 其中b(F)指的是F的Q-边界.即G/N∉F,但是G/N每个同态像都属于F,并且G/N有唯一的极小正规子群. 定理1设F是包含U的饱和群系, 记CG为C在G中的正规闭包. 群G∈F当且仅当对于M∈Uη(G), 存在关于M的s-完备C, 使CG/K(C)循环. 证明必要性的证明.若G∈F, 则G的每个极大子群是F-正规, 所以必要性显然成立. 充分性的证明.假设G∉F, 并且G是一个极小阶反例. 选取N◁G具有尽可能大的阶,使得G/N∉F, 那么G/N有唯一极小正规子群U/N,且U/N非循环. 由N的选取得G/U∈F, 即(G/N)/(U/N)=G/U∈F, 于是由GF的定义得(G/N)F≤U/N. 而U/N是G/N的唯一极小正规子群, 故U/N≤(G/N)F.于是U/N=(G/N)F=(GFN)/N. 定理2设F是包含U的饱和群系, 群G∈F当且仅当对于M∈Uη(G), 存在关于M的s-完备C,使得G=MC且C/K(C)的阶无平方因子. 证明必要性显然成立,下面只证充分性. 假设G∉F, 并且G是一个极小阶反例. 选取N◁G具有尽可能大的阶,使得G/N∉F, 那么G/N有唯一极小正规子群U/N. 由N的选取得G/U∈F, 即(G/N)/(U/N)=G/U∈F, 于是由GF的定义得(G/N)F≤U/N. 而U/N是G/N的唯一极小正规子群, 故U/N≤(G/N)F. 于是U/N=(G/N)F=(GFN)/N. (1) 存在M∈Uη(G), 使得N⊆M但U⊄M. 若Uη(G/N)=∅, 由定义1和引理6得G/N∈F, 矛盾. 所以Uη(G/N)≠∅, 即存在正规指数含有平方因子的极大子群M/N,使得U/NM/N. 从而存在G的极大子群M,使得N⊆M但UM, 即GFM, 所以M∈Uη(G). (2)U/N是非可解的特征单群. (3)K(C)=N,C是CU的极大子群且GF⊄C. 由(2)知,U/N非可解, 而C/K(C)可解. 由于所有的可解群组成的群类为子群闭的同态, 而U/N不属于这一群类, 所以由引理2知,可以选择C,使得K(C)=N, 且C是CU的极大子群. 若GF⊆C, 则U=GFN≤C. 由C/N可解知, (GFN)/N可解, 即U/N可解, 矛盾. 基于由低阶思维能力向高阶思维能力、从基础目标向高级目标发展的布鲁姆学习目标分类法,2016年中国药科大学进行了临床药学教育体系的大改革。新改的实践教学体系(图3)帮助学生提高对临床药学专业基础知识和专业知识的学习兴趣,对临床问题的分析、综合与决策能力,改善目前临床药学教学中注重灌输知识,忽视分析、评价、创新技能培养的坐而论道的教学方式,令学生的临床药学工作能力从低年级的初步认识逐步提升到高年级(毕业时)能够初步胜任临床药学工作的水平。 (4)G的每个极大子群H∈U(G)的指数均无平方因子. (5)C<·G. NU/N(PN/N)=C/N∩U/N=T/N. 假设C 显然,C∩U≤H∩U. 否则,C∩U 下面证明U/N≅PSL(2,r), 其中r为奇素数且CU [1] Asaad M, Li Shirong. On minimal subgroups of finite groups Ⅱ[J]. Comm Algebra, 1996, 24(14): 4603-4606. [2] Li Shirong. On minimal subgroups of finite groups Ⅲ[J]. Comm Algebra, 1998, 26(8): 2453-2461. [3] Wei Huaquan. Onc-normal maximal and minimal subgroups of Sylow subgroups of finite groups[J]. Comm Algebra, 2001, 29(5): 2193-2200. [4] Doerk K, Hawkes T. Finite Solvable Groups[M]. Berlin: Walter de Gruyter, 1992. [5] Li Shirong. OnF-abnormal maximal subgroups of finite groups[J]. Acta Math, 2007, 23(5): 885-888. [6] Zhao Yaoqing. On the Deskins completions, theta completions and theta pairs for maximal subgroups I[J]. Comm Algebra, 1998, 26(2): 3141-3164. [7] Li Shirong, Zhao Yaoqing. Ons-completions of maximal subgroups of finite groups[J]. Algebra Colloq, 2004, 11(3): 411-420. [8] Deskins W E. On maximal subgroups[J]. Proc Sympos Pure Math, 1959, 1: 100-104. [9] 徐明耀. 有限群导引[M]. 2版.北京:科学出版社, 1999. [10]Li Yangming, Wang Yanming, Wei Huaquan. The influency ofπ-quasinormal some subgroups of a finite group[J]. Arch Math, 2003,81: 245-252. [11]Skiba A N. On weaklys-permutable subgroups of finite groups[J]. J Algebra, 2007, 315(1): 192-209. [12]Gorenstein D. Finite Groups[M]. New York: Chelsea, 1980. [13]石向东, 韦华全, 马儇龙. 乘积因子群的共轭类长与有限群结构[J]. 郑州大学学报:理学版, 2013, 45(2): 10-13. [14]陈松良,蒋启燕. 关于108阶群的完全分类 [J].郑州大学学报:理学版, 2013, 45(1): 10-14. (责任编辑:王海科) OnF-Abnormal Maximal Subgroups ands-Completions GAO Hui, GAO Sheng-zhe, YIN Li (ScienceInstitute,DalianFisheriesUniversity,Dalian116023,China) LetFbe a saturated formation which contains all supersolvable groups. The structure of finite groups was characterized bys-completions ofF-abnormal maximal subgroups. Some necessary and sufficient conditions of the groups inFwere obtained. formation;F-abnormal maximal subgroups; normal index;s-completions 2015-01-12 高辉(1978-),女,辽宁庄河人,讲师,硕士,主要从事有限群研究,E-mail:gaohui@dlou.edu.cn;通讯作者:高胜哲(1974-),男,黑龙江大兴安岭人,副教授,硕士,主要从事有限群及金融数学研究,E-mail:gsz@dlou.edu.cn. 高辉,高胜哲,尹丽.关于F-反正规的极大子群与s-完备[J].郑州大学学报:理学版,2015,47(2):45-48. O152.1 A 1671-6841(2015)02-0045-04 10.3969/j.issn.1671-6841.2015.02.010
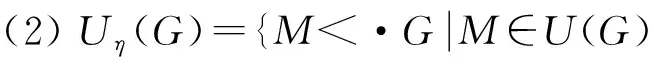





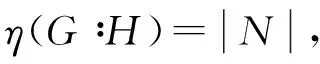
2 主要结果