基于图像特征改进的正交匹配追踪算法
2015-02-10田勇志王俊俏臧华平刘晓旻赵楠楠陈宝鑫梁二军
王 玲, 田勇志, 王俊俏, 臧华平, 刘晓旻, 赵楠楠 陈宝鑫, 梁二军
(郑州大学 物理工程学院 河南 郑州 450001)
基于图像特征改进的正交匹配追踪算法
王 玲, 田勇志, 王俊俏, 臧华平, 刘晓旻, 赵楠楠 陈宝鑫, 梁二军
(郑州大学 物理工程学院 河南 郑州 450001)
将压缩传感理论应用于成像是光场成像理论的热门研究方向,由此可以设计出更简单、便宜、小巧的光学系统.正交匹配追踪算法是压缩传感理论的重要重构算法,它在重建图像时隐含着整幅图像权重相同的思想,没有体现出图像的固有特征,例如行列突变的剧烈程度,以及经过快速傅里叶变换基、离散余弦变换基、离散小波变换基作用得到的小稀疏系数代表图像的细节、大稀疏系数代表图像的轮廓的特点.使用上述3种变换基作用图像时,可以针对正交匹配追踪算法的固有缺点,提出合理选择逐行或者逐列重构图像和使用自适应迭代次数重构图像两种改进方法.仿真结果表明,改进算法明显提高了图像的质量,能够得到更好的图像视觉效果.
光场成像; 正交匹配追踪算法; 压缩传感; 稀疏表示; 图像重建
0 引言
Candés和Donoho等人提出的压缩传感(compressive sensing,CS)理论[1-3]打破了奈奎斯特采样频率的约束,从而大幅度减少了传感器采集的数据量,降低了数据存储、传输、处理的成本.CS理论一经问世,便迅速应用于数字图像处理.2006年美国Rice大学设计的基于CS理论的单像素数码相机[4]相对于普通数码相机有许多突出的优点:节约储存、传输、处理的成本;响应波长从可见光扩展到红外和紫外;分辨率不再依赖于感光元件的面积,系统结构简单、小巧、便宜等.单像素相机不仅成功地验证了CS理论的正确性,而且为数码相机的发展开辟了一条新的道路.
重构算法是CS理论的核心内容和技术难点,它的优劣直接决定重构质量的高低.其中,贪婪算法是应用最为广泛的一类算法,主要包括:匹配追踪(match pursuit,MP)算法[5]、正交匹配追踪(orthogonal match pursuit,OMP)算法[6]、正则化正交匹配追踪(regularized orthogonal match pursuit,ROMP)算法[7]、子空间追踪(subspace pursuit,SP)算法[8]、压缩采样匹配追踪(compressed sampling match pursuit,COSaMP)算法[9]、逐步正交匹配追踪(stagewise orthogonal match pursuit,STOMP)算法[10]等.OMP算法是在MP算法的基础上,对已选择的原子集合进行正交化来保证迭代的最优性,从而减少迭代次数.它的理论框架简单,易于理解,重构速度快,具有很强的适用性.但是它的重建精度低,难以广泛地应用于存在噪声的高维信号问题,并且受限于迭代次数需要固定的要求.所以改进OMP算法一直是研究的热点.
图像经过稀疏变换基作用后得到有限的大系数包含了图像的绝大部分信息.目前常用的稀疏变换基[11]有:快速傅里叶变换基(FFT)、离散余弦变换基(DCT)、离散小波变换基(DWT)[12]等.它们是正交变换,并且变换速度快[13].例如,傅里叶变换将时域里的自然信号变换成“整个”时间范围内的“全部”频谱成分,离散余弦变换是离散傅里叶变换只包括余弦项的一种情况.小波变换是空间(时间)和频率的局部变换(图像经过小波变换后具有很多的优点[14],在工程技术上得到广泛应用[15]).这3种变换域显示的都是信号的频谱信息,其中高频信息的系数小,低频信息的系数大.对于图像,高频信息代表变化尖锐的细节部分,低频信息代表变化缓慢的轮廓部分.由于人眼分辨细节能力有局限性,图像重构时可以在达到人类视觉要求的前提下舍弃部分细节信息,以此来减少传感器获取的数据量.
由上述可知,使用FFT、DCT、DWT 3种变换基作用图像后,可以将图像特征应用到OMP算法中,克服OMP算法的固有缺点.因此,可以进行逐行或者逐列重构和使用自适应迭代次数重构两种方法恢复图像.仿真结果表明,改进算法重构图像的视觉效果更好.
1 合理选择逐行重构或者逐列重构
利用OMP算法重构图像时可以进行逐行或者逐列重构.逐行重构只考虑每行元素的特点,破坏了图像行与行之间的关联性,得到的图像横向失真比较严重.同理,逐列重构得到的图像纵向失真严重.因此,合理选择重构方式对提高图像的质量很重要.
如果一幅二维图像有P行Q列突变(每一行和每一列包括相同的像素),逐行重构会丢失P行的高频信息,逐列重构会丢失Q列的高频信息.所以,当P
为了验证上述理论,用列突变更频繁的图像(a)(有两行多列突变,每一行和每一列包括的像素值相同)、行突变更频繁的图像(b)(3列多行突变)、Lena图像(c)作为测试图像,进行仿真.在FFT、DCT、DWT 3种变换域里稀疏表示图像,然后用OMP算法重构图像,采取逐行和逐列重构两种方式,对比得到的图像质量.3幅原始图像、重构图像和图像质量的比较结果(以DWT为例)见图1~3及表1~3.

图1 列突变更频繁的图像(a)以及分别使用逐行和逐列重构得到的图像
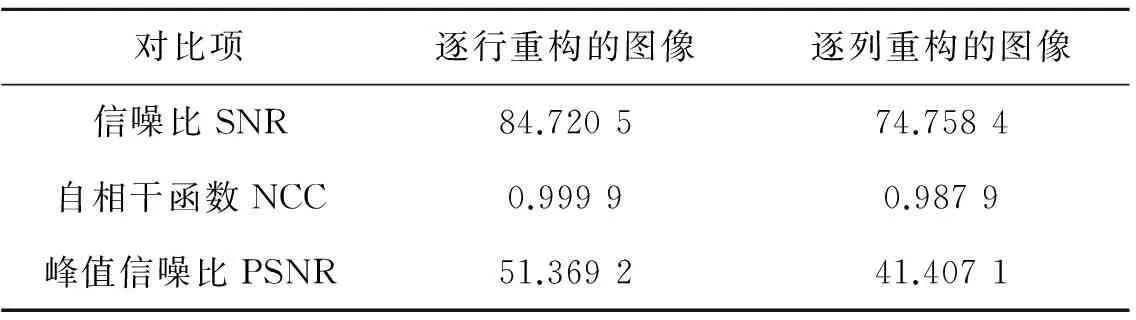
表1 对图像(a)进行逐行和逐列重构得到的图像的质量比较Tab.1 The quality comparison of images observed by using line by line and column by column reconstruction to image (a)

图2 行突变更频繁的图像(b)以及分别使用逐行和逐列重构算法得到的图像
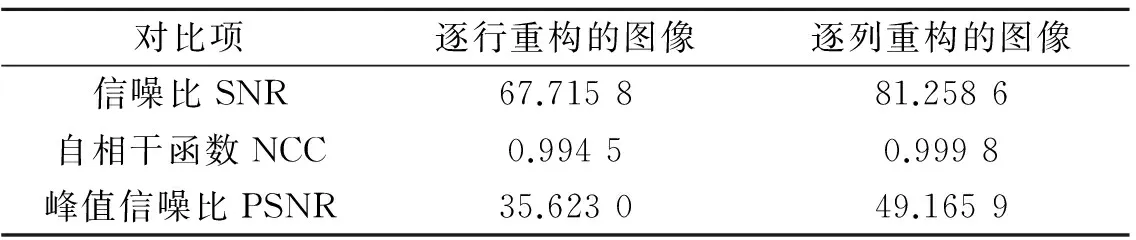
表2 对图像(b)进行逐行和逐列重构得到的图像质量的比较Tab.2 The quality comparison of images observed by using line by line and column by column reconstruction to image (b)

图3 Lena图像(c)以及分别使用逐行和逐列重构算法得到的图像
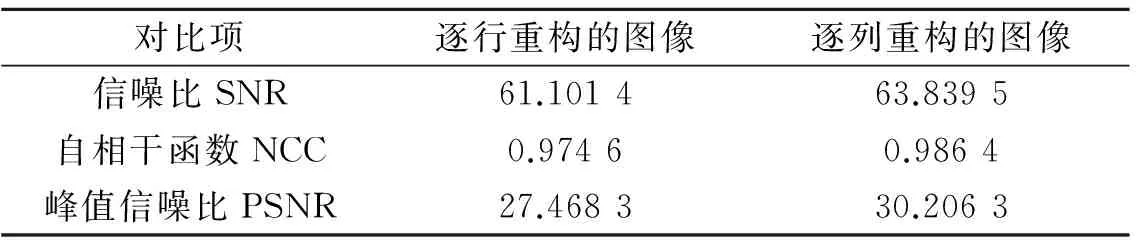
表3 对图像Lena (c)进行逐行和逐列重构得到的图像的质量的比较Tab.3 The quality comparison of images observed by using line by line and column by column reconstruction to Lena image(c)
可以从上面结果看出,用OMP算法重构时,对图像(a)进行逐行重构得到的像质更好,对图像(b)、(c)进行逐列重构得到的像质更好,图像(a)、(b)的测试结果容易理解,与理论吻合.对于图像(c)的结果可以如下理解:图像(c)中的人物的像素值变化更剧烈,图像的其余部分变化很缓慢,所以可以集中比较人物的行列的突变程度大小.近似将人物大小看成矩形,那么人物的高度明显大于人物的宽度,即人物突变的行数大于列数,行突变更频繁.所以,用OMP算法对图像(c)重构时,进行逐列重构得到的像质更好,与其结果吻合.因而由上述理论可知,合理选择逐行或者逐列重构对提高图像的精度相当重要.
虽然此理论需要手动选择重构方法,但是选择的方式简单易行,一旦选择出合理的重构方法后,能够大幅度地提高重构图像的质量,所以这种改进方法是可行的.并且,如果图像是可动的,只需要旋转图像90度,即可固定地使用同一种重构方法.
2 自适应迭代次数的正交匹配追踪算法
人眼对图像细节的分辨能力有限,图像重构时可以在满足人类视觉要求的前提下舍弃部分细节信息.比较经过DCT、FFT、DWT作用后的每列稀疏系数(逐行重构效果类似,以下只分析逐列重构)的大小,若某列包括越多的大稀疏系数,表明该列包含越多的低频信息,包含越多的图像信息,应该增加该列的迭代次数以恢复出图像的整体视觉效果.相反,若某列小稀疏系数越多,说明该列包含越多的细节信息,可以通过减少该列的迭代次数来适量地丢弃部分不影响视觉效果的细节.
可以先分析在相同迭代次数下重构得到的稀疏系数,比较每列系数绝对值的总和并排列大小,若某列系数绝对值的总和越大,表明此列包含越多的大稀疏系数.然后重新计算每列的迭代次数,其大小与每列系数绝对值的总和成线性正比,迭代次数的最大值和最小值的平均值等于第一次重构时每列的迭代次数(保证总的迭代次数不变),用自适应迭代次数第2次重构图像.其中,未改进算法的固定迭代次数和改进算法的最大、最小迭代次数都取决于图像的稀疏度.改进前,每一列的迭代次数相同,为图像的平均稀疏度.但是每一列包含的低频信息和高频信息是不同的,所以稀疏度不同.改进后,每列的迭代次数取决于此列的稀疏度.因为稀疏度的大小取决于因图像质量的要求而舍弃的接近于零的稀疏系数的个数,所以可以在固定迭代次数的基础上,根据每列的稀疏系数绝对值之和的大小,稍微改变舍弃的小的稀疏系数的个数,即改变该列的迭代次数.所以,每列迭代次数的取值(包括最大值、最小值)是根据原来算法的固定迭代次数上下浮动取值的.文中取线性关系的迭代次数是上述方法的一种简单计算的情况.因此,改进算法的流程如下:
1) 用未改进的OMP算法得到变换域里的稀疏系数;
2) 得到第i列稀疏系数绝对值的总和以及从小到大排列的顺序hi;
3) 设图像尺寸大小为M×N;第1次重构时,每列迭代次数为m0;第2次重构时,最多迭代次数为mmax,最少迭代次数为mmin,mmax+mmin=2m0;
第i列的迭代次数为mi=(mmax-mmin) (hi-1)/(N-1)+mmin;
4) 用自适应迭代次数第2次重构图像.
分别用改进前后的OMP算法重构Lena图像(c),对比得到的图像质量.原始图像、重构图像和图像质量的比较结果如图4和表4所示.

图4 Lena 图像(c)以及分别使用未改进和改进的算法重构的图像

表4 对Lena(c)使用未改进和改进的重构算法得到的图像的质量比较Tab.4 The quality comparison of images observed by using line byoriginal and improved reconstructed algorithm to Lena image(c)
从重构结果可看出,图像在FFT、DCT、DWT 3种变换基里稀疏表示后,通过自适应迭代次数重构的图像质量高于固定迭代次数重构的图像质量.虽然改进算法因为两次重构图像会增加恢复图像的计算时间,但是这种简单地重复使用OMP算法的方法来提高图像质量的思路是可行的.
3 结论
本文针对使用FFT、DCT、DWT 3种变换基作用图像后OMP算法以相同的权重处理整幅图像的缺点,提出了将OMP算法与图像特征结合来提高重构图像质量的两种方法:合理选择逐行或者逐列重构,利用自适应迭代次数重构.通过软件仿真,比较改进前和改进后算法得到的像质结果,可知改进的算法可以明显提高图像重建质量.
[1] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006,52(4):1289-1306.
[2] Candés E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006,52(2):489-509.
[3] Candés E J. Compressive sampling[C]//Proceeding of the International Congress of Mathematicians. Madrid, 2006,1443-1452.
[4] Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008,25(2):83-91.
[5] Mallat S, Zhang Z. Matching pursuit in a time-frequency dictionary[J]. IEEE Trans Signal Processing, 1993,41(12):3397-3415.
[6] Tropp J, Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans Inform Theory, 2007,53 (12):4655-4666.
[7] Needell D, Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Found Computer Math, 2009,9(3):317-334.
[8] Dai W, Milenkovic C. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Trans Inform Theory, 2009,55 (5):2230-2249.
[9] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Appl And Comp Harm Anal, 2009,26(3):301-321.
[10] Donoho D L, Drori I, Tsai Y, et al. Sparse Solution of Underdetermined Linear Equations by Stagewise Orthogonal Matching Pursuit[R].Stanford: Stanford University, 2006.
[11] Baraniuk R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007,24(4):118-121.
[12] Candés E, Donoho D L. Curvelets-a Surprisingly Effective Nonadaptive Representation for Objects with Edges[R].Stanford: Stanford University, 1999.
[13] 齐林,周立晓.变换域自适应滤波算法的研究[J].郑州大学学报:理学版,2007,39(1):61-66.
[14] 陈旭生,李艳灵.一种基于小波变换与分类矢量量化的图像压缩算法[J].信阳师范学院学报:自然科学版,2014,27(1):123-126.
[15] 刘雅琴,周炜.基于小波变换的说话人语音特征参数提取[J].河南科技大学学报:自然科学版,2005,26(4):44-46.
(责任编辑:王浩毅)
The Improved Orthogonal Match Pursuit Algorithm Based on Image Characteristics
WANG Ling, TIAN Yong-zhi, WANG Jun-qiao, ZANG Hua-ping, LIU Xiao-min,ZHAO Nan-nan, CHEN Bao-xin, LIANG Er-jun
(SchoolofPhysicsandEngineering,ZhengzhouUniversity,Zhengzhou450001,China)
Compressive sensing to images has become a hot topic in light field imaging theory due to that it can be applied in simple, cheap and small light systems. Orthogonal match pursuit algorithm was an important recovery algorithm in the compressive sensing theory. It assumed that the weight of the whole imaging was the same when reconstructed, ignoring the inherent characteristics of the imaging, such as the intensity of the mutations among lines and columns, and ignoring the characteristics that the small sparse coefficient represented the detail of the image and the big sparse coefficient represented the outline of the image. The sparse coefficient was acquired by the operation of fast Fourier transform basis, discrete Cosine transform basis, or discrete wavelet transform basis. Two methods were put forward to solve this problem, that is, reasonably choosing the line by line or column by column in reconstruction, and using adaptive iterations to reconstruct image, if the image was affected by the three kinds of transform basis mentioned above. Simulation results showed that the improved algorithm could significantly improve the quality of image.
light field imaging; orthogonal match pursuit algorithm; compressive sensing; sparse representation; image reconstruction
2015-01-11
国家自然科学基金资助项目,编号61307019;河南省科技厅重点科技攻关项目,编号132102210396;河南省教育厅科学技术研究资助项目,编号13A140693,14A14000;郑州市科技创新团队基金资助项目,编号112PCXTD337.
王玲(1989-),女,河南信阳人,硕士研究生,主要从事基于压缩传感的单像素成像研究,E-mail:fengqinglingzi@163.com;通讯作者:梁二军(1956-),男,河南新安人,教授,博士,主要从事光场成像研究,E-mail:ejliang@zzu.edu.cn.
王玲,田勇志,王俊俏,等.基于图像特征改进的正交匹配追踪算法[J].郑州大学学报:理学版,2015,47(2):73-77.
O438
A
1671-6841(2015)02-0073-05
10.3969/j.issn.1671-6841.2015.01.015
