不变子群基本定理以及相关例题

韩荣梅 内蒙古科技大学包头师范学院数学科学学院

一、不变子群的基本理论

定理1：一个群G 的一个子群N 是一个不变子群的充分而且必要条件是

a 为G 中任意一个元。

证明：假设N 是不变子群，则对于群G 的任意元a 来说，，所以有

假如对于G 的任何a 来说

那么

N 是不变子群。

定理2：一个群G 的一个子群N 是一个不变子群的充分而且必要条件是

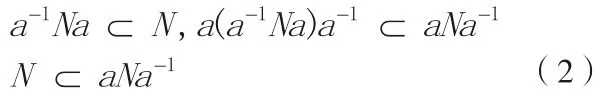
因此由定理1 得，N 是不变子群。

例1：证明：群G 的任意一个不变子群的交还是G 的一个不变子群。

证明：现只需要证，群G 中任意两个不变子群的交还是群G 的不变子群。

设N1、N2为群G 的两个不变子群，则有N1N2是G 的 子 群，则，并且，但N1、N2为群G 的两个不变子群，故，所以

例2：设H，N 是群G 的两个子群，证明：

（1）如果H，N 中有一个是不变子群，则HN 是群G 的一个子群；

（2）如果H，N 都是G 的不变子群，则HN 是群G 的一个不变子群。

证明：（1）若H，N 中有一个是不变子群，假如N 是群G 的一个不变子群，则在乘积HN 中任取两个元素a，b，并令

则由于H 是G 的子群，而N 是群G 的一个不变子群，所以

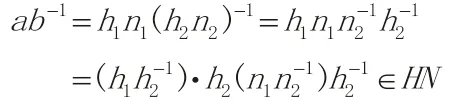
从而HN 是群G 的一个子群。

（3）设H，N 都是G 的不变子群，由（1）可知，HN 是群G 的一个子群，

所以HN 是群G 的一个不变子群。

例3 指数是2 的子群一定是不变子群。

证明：方法一：

令N 是群G 的一个指数是2 的子群，并且

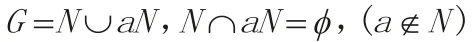
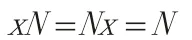
二、不变子群与商群

定义：群G 的不变子群N 的全体陪集对于陪集的乘法作成一个群，称G 是关于N 的商群，用符号来表示。

商群的阶数是N 在G 中的指数，若G是有限群，则

例4：证明：如果群G 只有一个n 阶子群，那么这个n 阶子群一定是G 的不变子群。

证明：设H 是群G 的一个n 阶子群，则对于G 中任意元素a，也是群G 的一个n 阶子群。

综上所述，H 为群G 的不变子群。

例5：置换群S4的不变子群N={E,(12)(34),(13)(24),(14)(23)}，求它的陪集组成的商群

以上的K1， K2， …， K6已经包含了S4中的所有元，现用S4的其他元素对N 作陪集，得到的结果与上面所得到结果相同。例如：

由上可制作如表一的商群的群表，例如：