基于产品长度的3重抽样均值控制图优化设计
2015-02-10王海宇
王海宇
(中原工学院 系统与工业工程技术研究中心 河南 郑州 450007)
基于产品长度的3重抽样均值控制图优化设计
王海宇
(中原工学院 系统与工业工程技术研究中心 河南 郑州 450007)
研究了3重抽样均值控制图的优化设计问题.分析了3重抽样均值控制图的平均产品长度分别在受控和失控情况下的计算方法,在此基础上建立了基于失控状态下平均产品长度最小化原则的控制图参数优化设计,并通过与原有的3重抽样均值控制图进行性能对比,验证了优化设计模型的有效性.
3重抽样控制图; 产品长度; 优化设计
0 引言
在统计质量控制中,休哈特控制图由于设置简单且易于计算,已经广泛应用于各类生产过程的质量监控.休哈特均值控制图是应用范围最广的一种控制图方法,主要用于监控过程均值的变异,当过程均值发生较大的偏移时,休哈特均值控制图能快速有效地发现过程异常,但当过程均值发生微小偏移时,这种控制图方法的监控效果不佳.为了提高对微小偏移的监测效率,人们对控制图的设计和抽样方式进行了改进,包括变化抽样区间的均值(variable sampling intervals,VSI)控制图、变化样本容量(variable sampling size,VSS)控制图、双抽样(double sampling,DS)控制图等,并由此形成了动态控制图这一新的研究领域[1-2].DS控制图将二次抽样检测的概念结合到控制图理论中,采用两个阶段的抽样来监控过程,这种方法能降低抽样数量并提升检测过程偏移能力[3].Costa曾比较了VSS、VSI和DS控制图,结果发现DS控制图的监测效率最高[4].Lee等将双抽样技术和可变抽样间隔结合起来,形成了变化抽样区间的双抽样控制图[5].Rodriguez将DS控制图方法应用于计数型数据,构造了双抽样NP控制图[6].He等对DS控制图的思想进行了延伸,提出了3重抽样(triple sampling,TS)控制图,采用3个阶段的抽样来监控过程,能够比DS控制图有更好的监控效果[7].但是,He等在设计TS控制图时,沿用了Irianto 和Shinozaki的DS控制图多目标决策的设计方式[8],在多个统计指标的情况下,很难客观判别TS控制图的监控效果[9].因此,本文从效率优化的角度出发,构建TS控制图的优化参数设计方案.
1 TS控制图
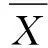
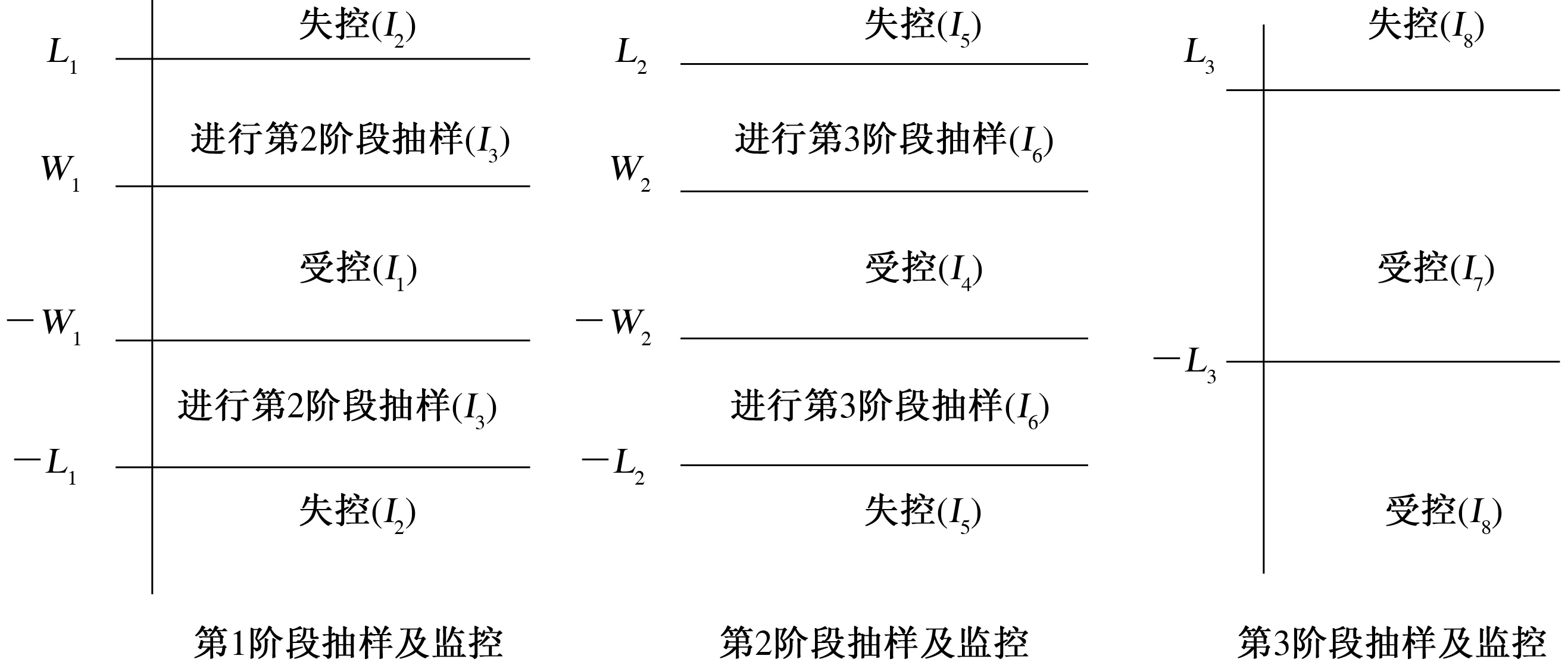
图1 TS均值控制图
2 TS控制图的效率评价
对于控制图性能的度量,平均运行长度(ARL)是最常采用的一个指标,它表示从过程发生异常质量波动到该异常质量波动被控制图发现平均需要的样本数.对于TS控制图,若过程处于稳定状态,通常用ARL0=1/α表示,其中α为控制图第1类错误的概率;若过程出现异常,可以用σ(过程服从分布的标准差)的倍数表示过程均值偏移的程度(即δσ),此时用ARLδ=1/(1-βδ)表示,其中βδ为控制图第2类错误的概率.α和βδ的计算见式(1),(2).α=P(z1∈I2)+P(z2∈I3)×P(z2∈I5)+P(z1∈I3)×P(z2∈I6)×P(z3∈I8)=
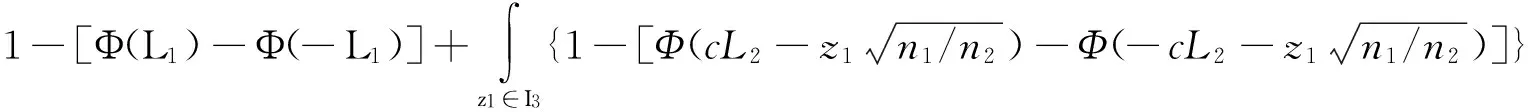
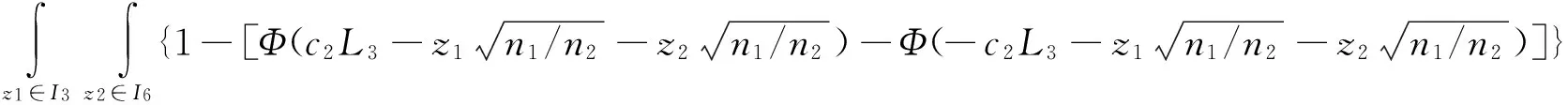
(1)

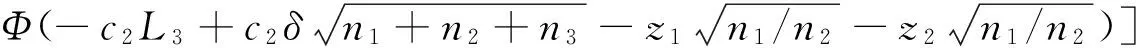
(2)
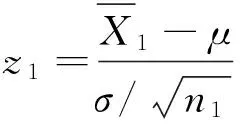
P(·)表示落在某区域的概率,Φ(·)表示标准正态分布的累计分布函数,φ(·)表示标准正态分布的概率密度函数.对于3重抽样均值控制图,过程稳定时的期望样本量E0(n)和过程偏移程度为δ倍标准差δσ的期望样本量Eδ(n),可以分别通过以下公式计算:
E0(n)=n1+n2P(z1∈I3)+n3P(z1∈I3)×P(z2∈I6)=
n1+n2·[Φ(-W1)-Φ(-L1)+Φ(L1)-Φ(W1)]+
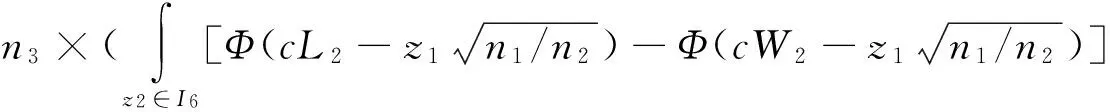
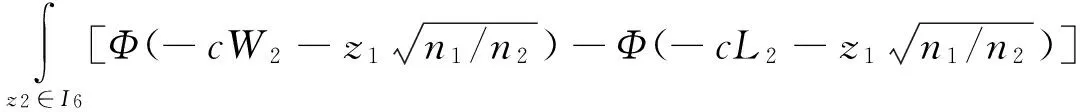
(3)
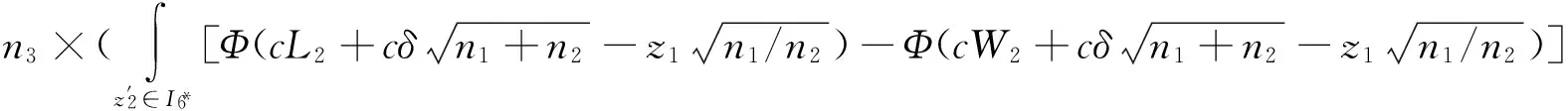
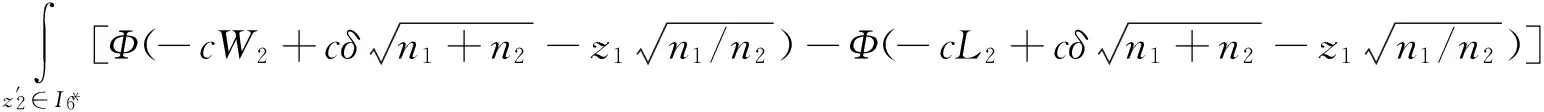
(4)
要提高TS控制图的监测效率,不仅需要失控情况下的平均运行长度ARLδ尽可能小,而且受控情况下样本容量的数学期望E0(n)和失控情况下样本容量Eδ(n)也应该尽可能小,因此仅应用平均运行长度不足以有效衡量其监控效率.Keat等提出的平均产品长度(average product length,APL)不失为一种更有效的效率度量指标,指从过程出现异常到该异常在控制图中被发现之间平均生产的产品数量[10].于是受控和失控时的平均产品长度分别为:
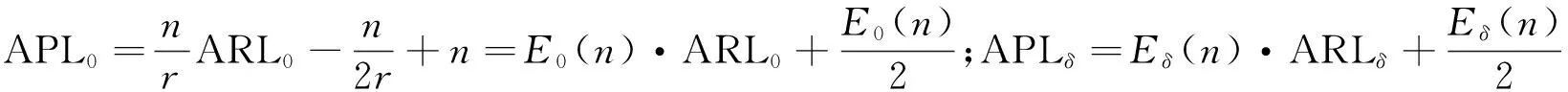
(5)
其中,r为抽样频率,为了计算简便,不失一般性,取r=1.
3 TS控制图的优化设计
TS控制图的设计需要确定8个参数:3个控制限参数(L1、L2和L3)、3个阶段的抽样数(n1、n2和n3)、以及第1阶段和第2阶段的警告限参数(W1和W2).由于在实际控制图应用过程中,若过程稳定,希望错误报警的概率要小,即ARL0尽量大,同时样本容量的数学期望E0(n)也要尽量小;当过程中出现异常波动时,希望能尽快发现,即ARLδ越小越好,同样样本容量的数学期望Eδ(n)也要尽量小.但二者互相影响,不能同时达到最优,因此可以让ARL0取一个足够大的固定值D,而E0(n)取一个适当的较小值n0,如按照常规控制图的设计思想,希望受控状态下的ARL为370,样本容量为3~5,在此基础上要求APLδ达到最小. 由此可采用如下TS控制图的设计模型:
MinAPLδ
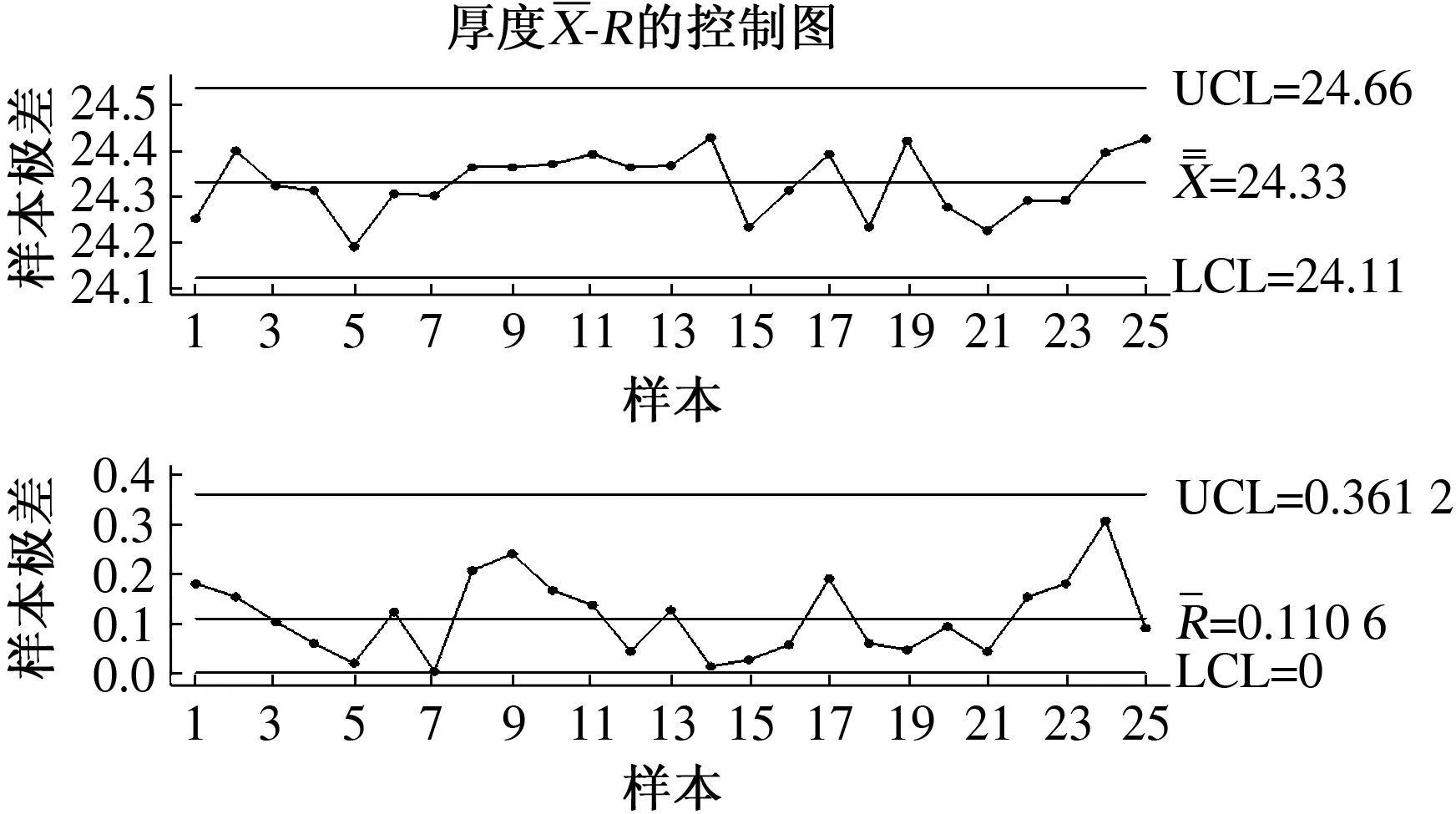
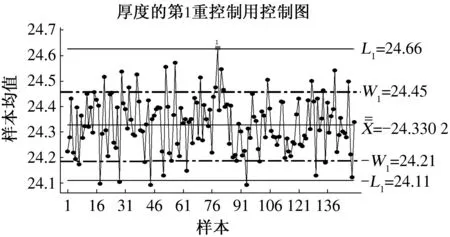
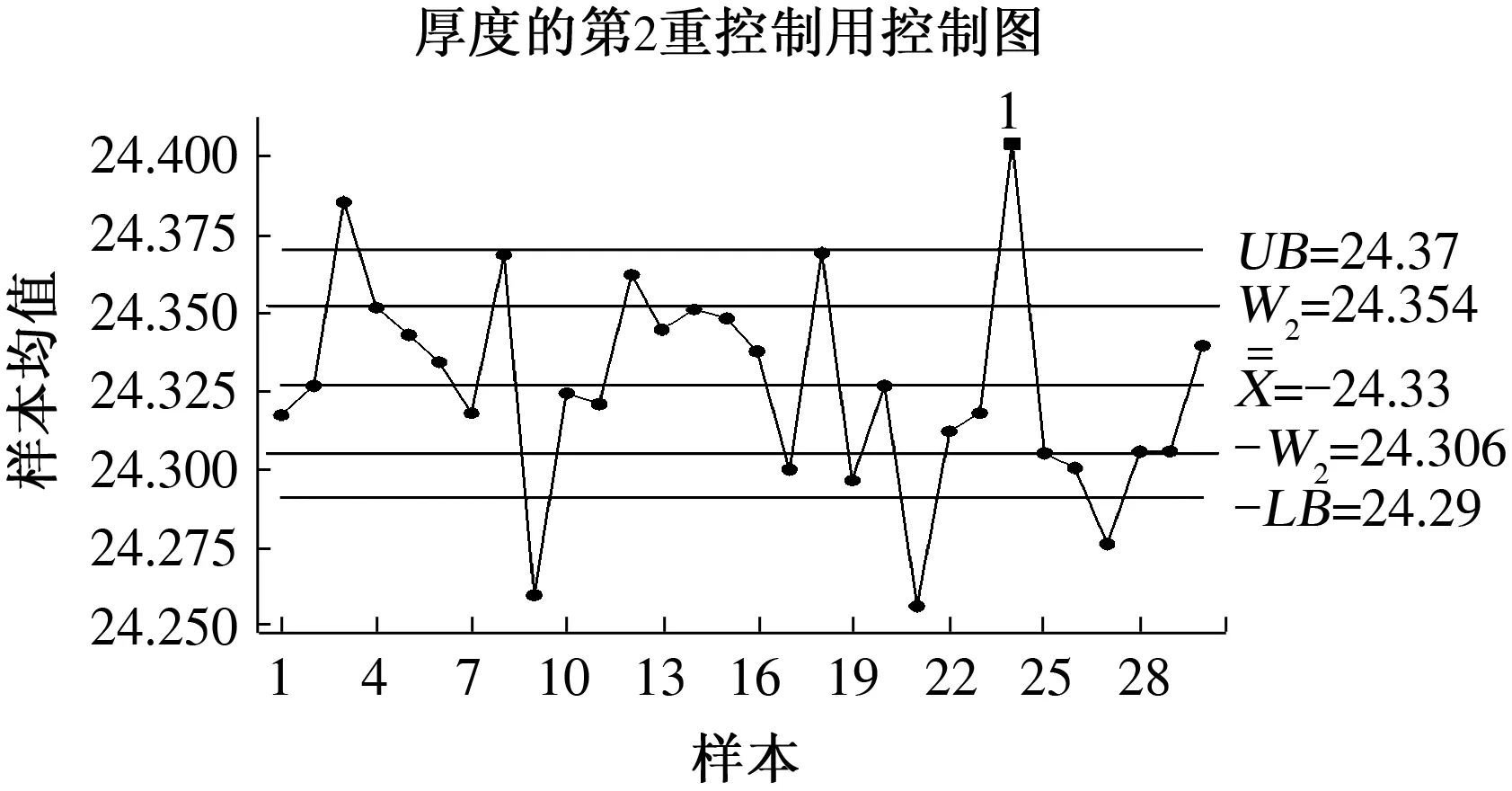
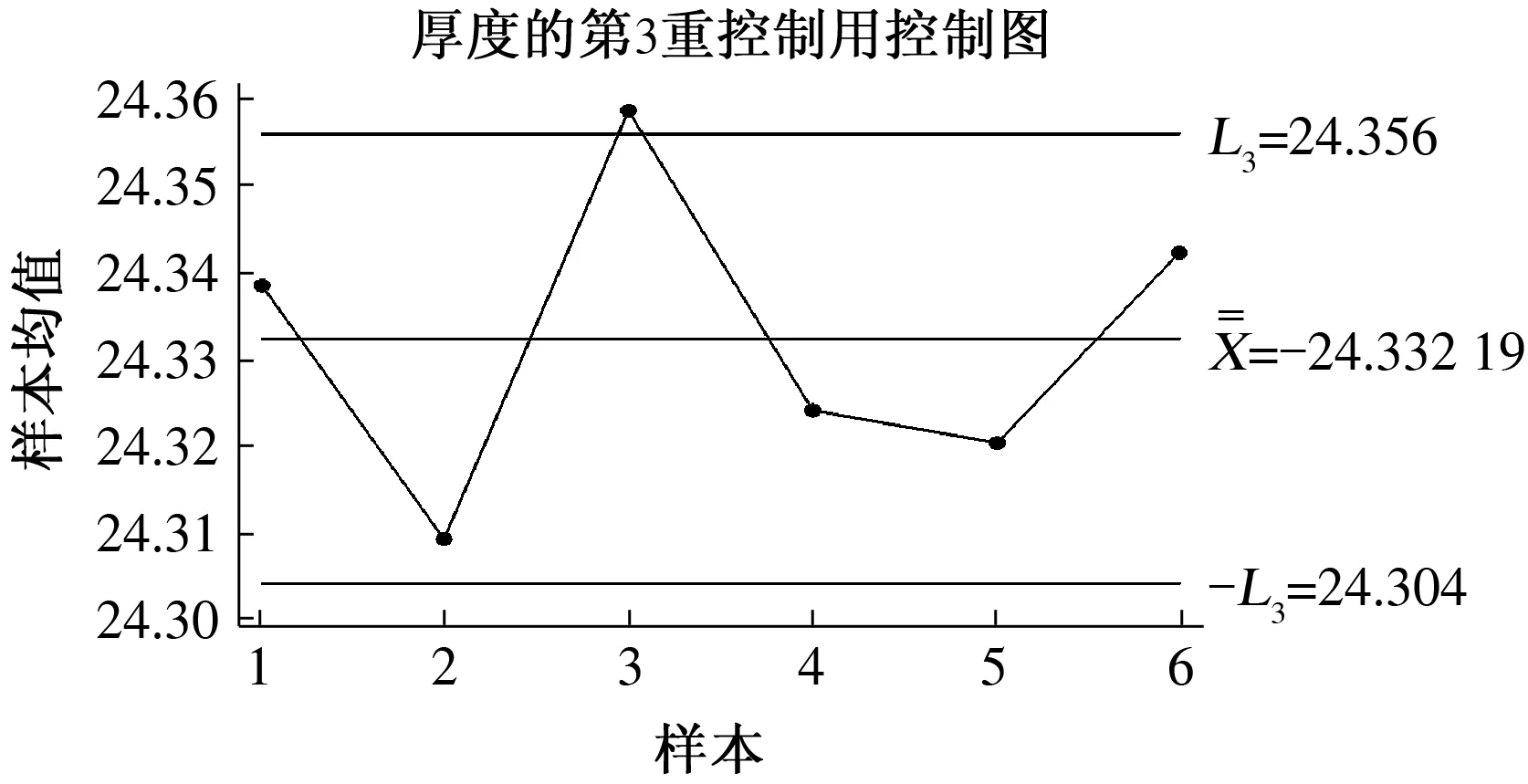
约束:ARL0=D;E0(n)=n0;1 (6) 其中,3个阶段的抽样样本容量(n1、n2和n3)必须是正整数,且n3>n2>n1,这是为了保证第2阶段控制图的检测效率高于第1阶段控制图的检测效率,第3阶段控制图的检测效率高于第2阶段控制图的检测效率;第1、第2阶段警告限参数Wi都要小于同一阶段的控制限参数Li,且Li也不能太大,可以设定控制限上限值为L′. 为了说明该设计方案的有效性,可以与He等的设计方案[7]进行对比分析.为了使两种方案具有可比性,在He等的设计方案中,α′=0.002 7,转换成受控状态下的平均运行长度ARL0约为370.在本文的设计中,同样设定D=370,n0=3.在两种方案中,为了减少计算量,3个阶段的抽样样本容量都取小于30的数,控制限上限L′=5.用本文优化设计模型和He等的设计方案分别针对1倍、2倍和3倍标准差的过程异常偏移进行设计来确定最佳的控制参数,再分别用两种方案对不同程度的过程偏移进行监控效率的对比,采用Matlab编程计算,结果见表1. 从表中的对比可以发现,绝大多数情况下,本文提出的优化设计方案的ARLδ、Eδ(n)和APLδ都要比He等的设计方案要好,尤其是在过程出现异常波动较小的情况(如δ=1.0)下.在ARL0相同的情况下,监控所需用的样本容量E0(n)和Eδ(n),以及失控状态的检出效率ARLδ和APLδ都要比He等的设计方案小得多,说明这种优化设计模型克服了He等的设计方案存在的多目标决策不利于效率最优化的不足,有效提高了TS控制图的监控效率. 表1 两种设计方案的监控效率对比Tab.1 Performance compare of two design schemes 某电路板加工过程将电路板厚度作为关键质量特性进行控制图监控,为了提高控制图对过程中出现的较小偏移的灵敏性,拟采用TS控制图方法.根据上一节优化设计的分析可知,对于较小的过程偏移δ=1.0,TS控制图的优化设计参数为,n1=2,n2=7,n3=12,L1=3.21,W1=1.76,L2=3.34,W2=1.92,L3=2.77.按照此优化设计参数构造TS控制图,具体步骤如下: 图2 分析用控制图 图3 第1重控制用控制图 图4 第2重控制用控制图 图5 第3重控制用控制图 本文主要讨论了3重抽样均值控制图的优化设计模型.通过对3重抽样控制图设计方案进行评价指标改进,构建了新的优化设计模型,通过与原有设计方案的对比发现,新的优化设计模型能够有效提高该控制图技术检测各种程度异常偏移的有效性. [1] Costa A F. JointXandRcharts with variable sample size and sampling intervals[J]. Journal of Quality Technology,1999,33(1):387-397. [2] Croasdale P. Control charts for a double sampling scheme based on average production run length[J]. International Journal of Production Research,1974,29(6): 585-592. [4] Costa A F,Rahim M A. JointXandRcharts with two stage sampling[C]//Proceedings of IIE Research Conference. Orlando,Fla,USA,2002. [5] Lee P,Chang Y,Torng C. A design ofScontrol charts with a combined double sampling and variable sampling interval scheme[J]. Communications in Statistics: Theory & Methods, 2012,41(1): 153-165. [6] Rodriguez D A, Epprecht K, Demagalhaes S, et al. Double-sampling control charts for attributes[J]. Journal of Applied Statistics,2011,38(1): 87-112. [10]Keats J B,Miskulin J D,Runger G C. Statistical process control scheme design[J]. Journal of Quality Technology, 1995,27(1): 231-246. [11]Torng C,Tseng C. Non-normality and combined double sampling and variable sampling interval control charts[J]. Journal of Applied Statistics,2010,37(6): 955-967. (责任编辑:王浩毅) The Optimal Design of Triple Sampling Mean Control Chart Based on Product Length WANG Hai-yu (CenterofSystem&IndustrialEngineering,ZhongyuanUniversityofTechnology,Zhengzhou450007,China) The optimal design of triple sampling mean control chart was discussed. The calculating methods of average product length for in-control and out-of-control processes of this chart were proposed,and the optimal model of parameters design of triple sampling mean control chart was constructed to minimize average product length for out-of-control process. Moreover,the effectiveness of this model was demonstrated by comparing with the old design method of this chart. triple sampling control chart; product length; optimal design 2015-01-16 国家自然科学基金资助项目,编号71002073;河南省高校科技创新人才支持项目,编号15HASTIT011;河南省高等学校人文社会科学重点研究基地资助. 王海宇(1979-),男,山西晋城人,博士,副教授,主要从事质量管理研究,E-mail: wanghy1979@126.com. 王海宇. 基于产品长度的3重抽样均值控制图优化设计[J].郑州大学学报:理学版,2015,47(2):121-126. TB114.2 A 1671-6841(2015)02-0121-06 10.3969/j.issn.1671-6841.2015.02.024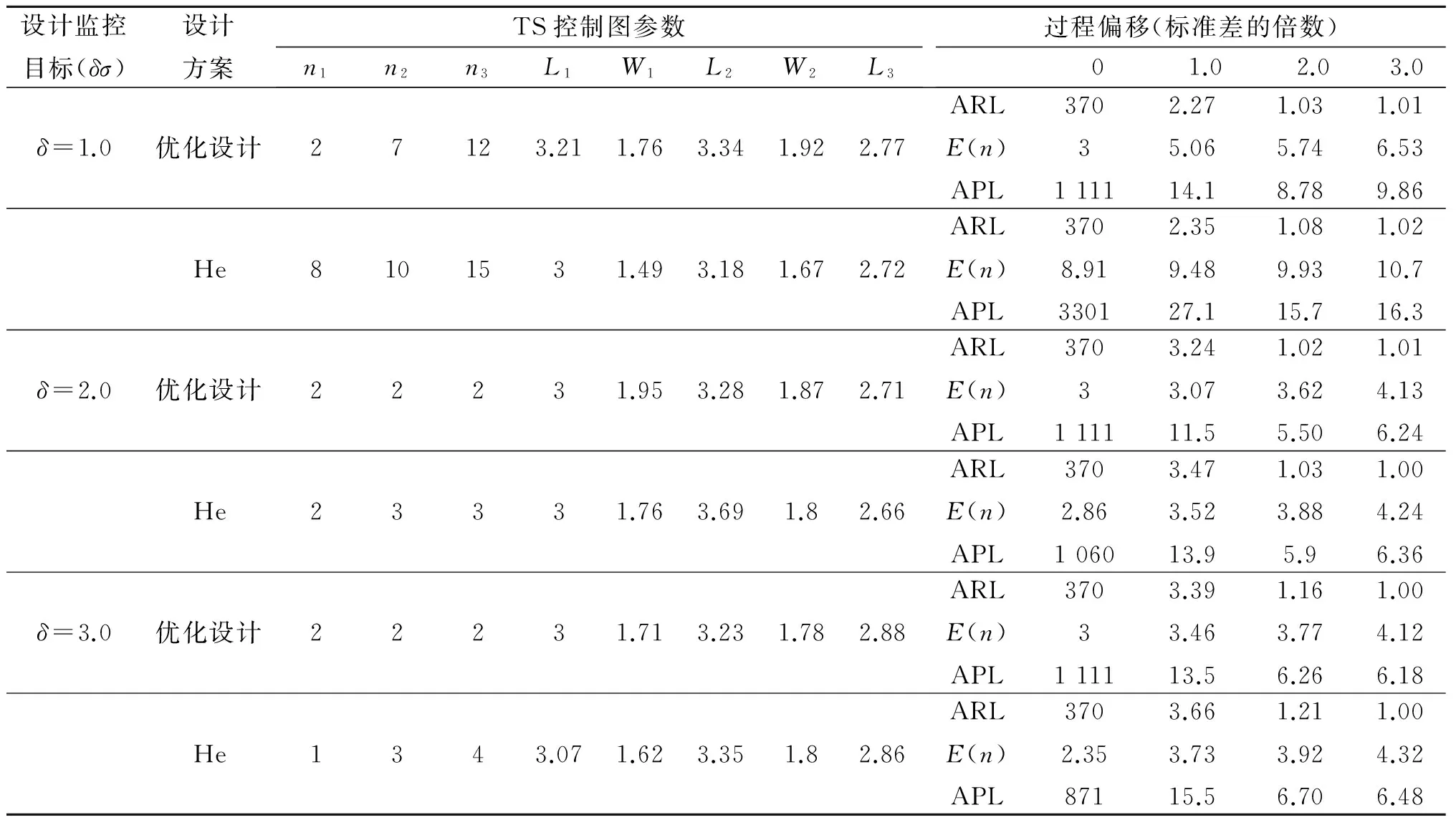
4 应用实例
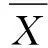

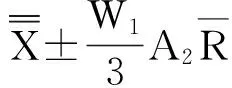
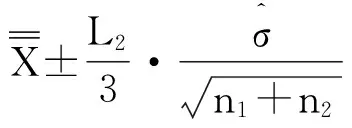
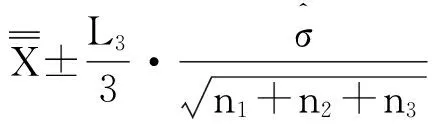
5 结论