一种改进的GPS整周模糊度单历元求解法

叶 培，安立宝

（1.武警黄金第十二支队，四川成都610036，2.中国黄金集团阳山金矿有限公司，甘肃文县746400）

一种改进的GPS整周模糊度单历元求解法

叶 培1，安立宝2

（1.武警黄金第十二支队，四川成都610036，2.中国黄金集团阳山金矿有限公司，甘肃文县746400）

快速准确地确定整周模糊度是进行高精度GPS测量的关键问题。根据阳山金矿控制测量的自身特点，对刘宁等人提出的新GPS整周模糊度单历元求解法进行改进，简化模糊度搜索空间，增加单频机采集数据的算法，通过线性组合逆变化求取模糊度，以模糊度函数法进行真值的搜索，实现单历元解算。在阳山矿区GPS控制测量中随机选取两条基线进行解算，从而证明此法的可行性和可靠性。

整周模糊度；单历元；阳山矿区；模糊度搜索空间

0 引 言

快速准确地确定整周模糊度是进行高精度GPS测量的关键问题，目前较为常见的模糊度解算方法有最小二乘搜索法[1，2］、快速模糊度搜索的滤波法[3］和最小二乘模糊度降相关平差法[4］等。这些方法各有优点，但也有其局限性，主要表现在需先进行相位周跳的探测与修复，且当卫星信号被遮挡时，需要对整周模糊度重新求解。刘宁等人提出了一种新的GPS整周模糊度单历元求解法[5］，不需要较为准确的先验约束信息便能得到高精度测量值。但是各个测区，有其自身特点，这种方法是不是在每个测区都能得到较为可靠的精度，是一个值得探讨的问题。

武警黄金第十二支队从2000年开始，在甘肃省文县阳山金矿带陆续进行了大面积的GPS控制测量，其中D级控制测量面积为198km2，E级控制测量面积为87km2，整个GPS控制测量时间经历了近13年的时间。阳山金矿测区属于秦岭造山带，地形复杂，切割较大，植被茂密，部分地区还有池塘和湖水对卫星信号起一定反射作用，而且2005年以前采集数据的机器还为单频机，如何根据测区自身特点来对这个新算法进行一定改进以提高GPS精度，就显得很有必要。

1 模糊度单历元改进算法的思路

1.1 模糊度搜索空间的简化

按照刘宁提出的模糊度的搜索空间数学公式为[5］

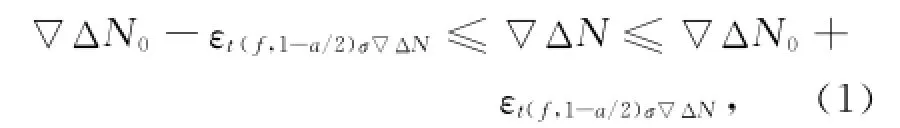
式中，εt（f，1－a/2）σ∇ΔN为置信度为（1－a）时，由自由度为f的t－分布概率密度函数所得到的双尾置信区间的上下界宽[6］。利用码伪距双差观测值进行最小二乘定位得到的点位中误差为.

双差模糊度反算公式为[7］

∇ΔN＝∇Δρ/λ－∇Δφ.（2）

通过式（2）计算初始模糊度为∇ΔN0，并让＝σΔx，则由式（1）可以确定模糊度搜索空间的大小。

安置在基线两端点的1、2同步观测卫星Sj、Sk的双差观测方程为

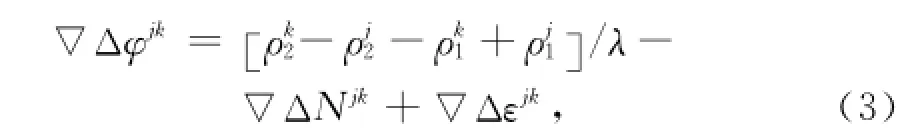
式中：∇Δφjk为双差相位观量；卫星S到接收机R间的距离为（R＝1，2，S＝j，k）；∇ΔNjk为双差整周模糊度；λ为波长；∇Δεjk为观测噪声。基线两个点，点1为已知点，点2为未知点，那上面算式的主要误差会存在于.

阳山矿区所在区域为秦岭造山带，该地区地形特点为，切割大，植被发育茂盛，部分控制测量区域有河水和池塘，对卫星信号有一定反射作用，根据这种地形特点，结合误差的主要存在方向，将式（1）中的a取值修正为0.30%，对应的εt（f，1－a/2）≃3.3[6］，同时可以得到模糊度精度算式为

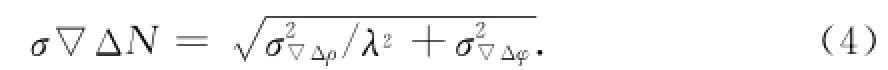
1.2 基于线性组合的模糊度变换

从式（1）和式（4）可以看出，整个解算虽有一定的简化，但真正计算起来还是较为繁琐，为了进一步减少计算量，采用双频线性组合扩波技术。

假设L1和L2的双差载波相位为∇Δφ1和∇Δφ2，则双频线性组合可表示为[8］

∇Δφ（α，β）＝α∇Δφ1＋β∇Δφ2.（5）

令λ1、λ2和∇ΔN1、∇ΔN2分别为∇Δφ1和∇Δφ2的波长及模糊度，则组合相位的波长和模糊度为[7－8］

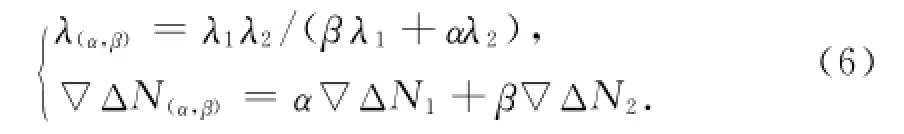
利用式（5）和式（6）可以推导出线性组合后的模糊度变换公式为

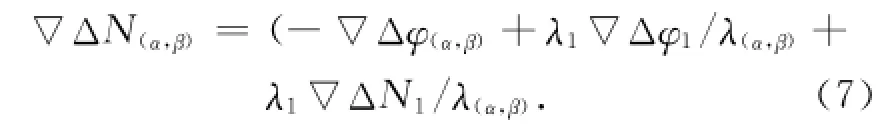
从式（7）可以发现，选择合适的α和β，使λ（α，β）＞λ1，则模糊度∇ΔN（α，β）的搜索空间相对于∇ΔN1的空间缩小，从而提高模糊度解算度的效率。

1.3 N1及N2模糊度确定的改进

根据刘宁等人提出的新算法的思路，首先定义模糊度函数值AFV的计算公式为

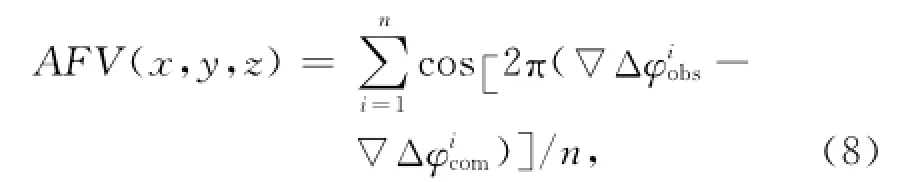
式中：n为一个历元上所组成的双差观测值数；∇Δφiobs表示双差观测值；∇Δφicom表示双差计算值。将所有L（1，－1）的双差观测值及其计算值代入式（8），并计算该位置的AFV，取其中满足AFV＞δAFV的模糊度向量组成候选模糊度集合ΩNw.对ΩNw中的每一组模糊度组合进行双差最小二乘固定解，并以方差因子最小的原则确定正确基线。刘宁等人之后提出用线性组合的方法来构建转换关系。阳山控制测量由于经历时间较长，早期采集的数据由于物质条件的限制，采用的是GPS单频机，这部分数据，就只有L1一个单差载波，相信很多大型矿区勘探和开挖生产两个阶段都会经历十年以上的时间，难免也会遇到同样的问题，作者根据唐卫明[9］提出的两步搜索整周模糊度算法，对这个线性组合算式进行改进，将单频和双频两种机器的差别考虑进去，改进算式为

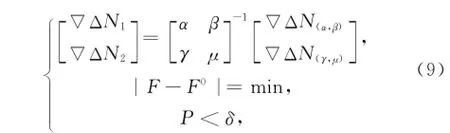
式中：∇ΔN（α，β）和∇ΔN（γ，μ）是两种线性组合的模糊度，对他们进行逆变换求取的整周模糊度为∇ΔN1和∇ΔN2.F为已知基线长；F0为计算基线长；δ取值为10mm；P为N组整周模糊度组合成功的概率为

式中，ρ为每组整周模糊度的成功率（ρ1＋…＋ρn≤1，0≤ρi≤1）。尽量选取波长较长、噪声较小并具有良好特性的线性组合[10］，所以γ＝－1，μ＝2（其波长为λ（－1，－2）≃34.1cm）。利用式（7）进行模糊度变换得到模糊度组合∇ΔN（－1，2）的搜索区间并由式（8）获取其候选模糊度集合ΩNn.

在获取模糊度集合后，利用双差相位观测值或者是单差相位观测值代入式（9）计算相应的单位权方差因子，再将其结果进行大小排列，设定最小值为，次小值为，引入搜索因子Ratio进行真值判断[11］为

假如Ratio的数值大于某一阈值时，可认为模糊度的最优解和次优解得到区分，即为解算成功，并选取σ2min对应的模糊度和基线解为最终的单历元解算结果。

2 改进算法在阳山金矿控制测量中的验证

随机地从阳山金矿采集的GPS数据选择两条基线，双频机采集数据为A基线，单频机采集数据为B基线，截至高度角设为13°，两条基线采样间隔均为15s，双频机为中海达V30，单频机为TRIMBLE4600LS，基线长度分别为4 796.391m和2 929.748m，历元分别为324和315，全文数据采用TBC软件进行处理，将其解算的结果作为分析本文改进方法解算基线质量的参考值，计算改进方法得到的固定解与参考值之差。

从表1可以看出，两条基线使用改进算法，成功率都在98%以上，比传统方法成功率提高了近2个百分点，且RMS值较小，从而说明了该改进算法的可行性和可靠性。同时，不难发现基线B解算成功率和精度都低于基线A.分析原因，一方面是采集数据机器的性能差异，另一方面也不排除基线B附近水面较多，对卫星信号有一定的影响，从这个角度来说，这个改进算法还有进一步改进的空间。

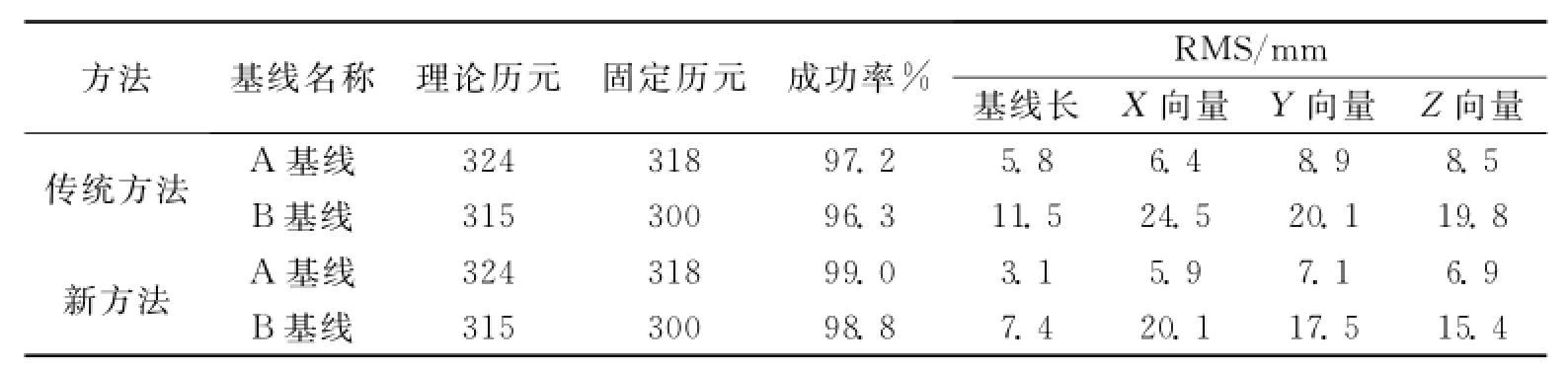
表1 两条基线求解的精度信息

3 结束语

运用刘宁等人提出的新GPS整周模糊度单历元求解算法，结合阳山金矿控制测量的自身特点，引入唐卫明等人提出的两步搜索算法，进行改进，减化模糊度空间搜索，增加单频机采集数据的情况，以达到完善算法、简化算法的效果。这种改进解算法仅采用一个历元的码和相位观测值进行模糊度的分解和基线解算，避免了GPS载波相位数据中的周跳探测与修复问题，使得GPS数据处理过程的计算量减少不少。采用的这种改进算法，目前已经在黄金部队多个矿区GPS控制测量试用，已收到良好的效果。

[1]刘智敏，刘经南，姜卫平，等.遗传算法解算GPS短基线整周模糊度的编码方法研究[J］.武汉大学学报·信息科学版，2006，7（31）：607－609.

[2]FREI E，BEUTLER G.Rapid static positioning based on the fast ambiguity resolution approach“FARA”：theory and first results[J］.Manuscript Geodatetica，1990（15）：325－356.

[3]HATCH R R，SHARP T.A computationally efficient ambiguity resolution technique[C］//In proceeding of on GPS 2001，Salt Lake city，UT.USA.2001：11－14.

[4]TEUNISSEN P J G.A new method for fast carrier phase ambiguity estimation[C］//In Proceedings of the IEEE PLANS’94，Las Vegas，NV，11－15April 1994：562－573.

[5]刘 宁，熊永良，王德军，等.一种新的GPS整周模糊度单历元求解算法[J］.武汉大学学报·信息科学版，2013，38（3）：291－294.

[6]LIN S G，TZENG D B.Single epoch kinematic GPS positioning technique in short baseline[J］.Journal of Surveying Engineering，2006，132（2）：52－57.

[7]MOK E.Reliable single epoch GPS processing algorithm for static deformation monitoring[C］//Symposium on Geodesy for Geotechnical and Structural Engineering，Eisenstadt，Austria，1998.

[8]XU G C.GPS theory，algorithms and applications[M］.2nd ed.Berlin：Springer－Verlag，2007.

[9]唐卫明，孙红星，刘经南.附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J］.武汉大学学报，2005，30（5）：444－446.

[10]刘 超，王 坚，许长辉，等.基于经验模态分解的GPS/伪卫星组合基线解算模型[J］.武汉大学学报·信息科学版，2010，35（8）：996－1000.

[11]李征航，张小红.卫星导航定位新技术及高精度数据处理方法[M］.武汉：武汉大学出版社，2009.

An Improved GPS Ambiguity Single Epoch Solving Method

YE Pei1，AN Libao2
（1.Gold Twelfth Detachment of the Armed Police，Chengdu610036，China；2.China National Gold Group Yangshan Gold Limited，Wen County746400，China）

Quickly and accurately determine the integer ambiguity is a key issue carried out high－precision GPS measurements.The authors measured according to the Yangshan gold mine to control its own characteristics，the new GPS Ning et al proposed integer ambiguity single epoch solving method to improve and simplify the search space of ambiguity，single－frequency machine algorithms to increase data collection through linear combination of inverse variation strike ambiguity to ambiguity function method to search the true value of single－epoch solver.In Yangshan mine GPS control survey randomly selected two baseline solver，thus proving the feasibility and reliability of this method.

Integer ambiguity；single epoch；Yangshan mining；ambiguity search sp ac

P228.4

A

1008－9268（2015）01－0061－04

10.13442/j.gnss.1008－9268.2015.01.013

叶 培（1978－），男，硕士，工程师，长期从事工程测绘工作。

2014－08－22

联系人：叶培E－mail：125140884＠qq.com