基于预报的实时卫星钟差完好性监测算法比较

吴传龙，陈 慎，张海涛，刘 梦

（1.61175部队，湖北武昌430000；2.61243部队，甘肃兰州730000）

基于预报的实时卫星钟差完好性监测算法比较

吴传龙1，陈 慎1，张海涛1，刘 梦2

（1.61175部队，湖北武昌430000；2.61243部队，甘肃兰州730000）

利用钟差历史数据建立卫星钟差模型，提出了基于预报钟差的卫星钟差完好性监测算法，并对比分析了采用最小二乘算法和遗忘因子最小二乘算法对钟差异常监测的效果，结果表明：遗忘因子最小二乘算法监测效果明显优于最小二乘算法。

卫星钟差；完好性；实时监测；遗忘因子最小二乘

0 引 言

卫星钟差在精密定位中占有重要的地位，钟差纳秒级的误差引起的等效距离误差可达分米甚至是米级，其准确与否将直接影响用户的定位精度，从用户角度而言，卫星钟差的完好性比精度有着更加重要的地位，因此，研究卫星钟差的完好性算法具有重要的现实意义[1］。目前卫星钟差的完好性监测主要是依靠地基辅助技术实现，利用地面监测站监测卫星钟的完好性，但其对地面依赖程度高、费用昂贵、及时告警能力差。卫星钟的完好性监测主要是监测卫星钟差异常，还可以通过动态Allan方差、平均滑动滤波等算法和基于滑动窗口的最小二乘拟合算法实现，这些算法虽然能够监测卫星钟差异常情况，但在实时性上它们很难满足提供实时定位服务系统的需要，尤其无法满足基于区域参考站网络的实时精密单点定位[2－6］。本文提出利用钟差历史数据建立卫星钟差模型，采用实时更新的固定长度的钟差数据的算法实时监测卫星钟差异常，并通过实验进行了验证。

1 卫星钟差完好性监测算法

1.1 卫星钟差预报模型

卫星钟差完好性监测需要卫星钟时钟频率具有足够的稳定性，以保证时钟偏差是可以预测的，一般采用二次多项式模型，表示为矩阵形式[6－7］为

式中，H为n×3维设计矩阵

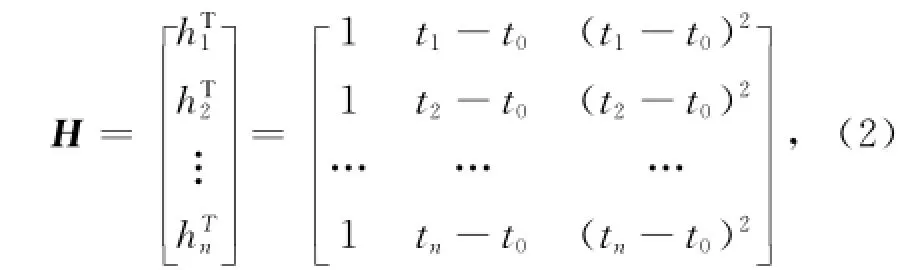
式中：X为n维观测向量；a＝[a0a1a2］T为3维未知参数向量，a0、a1和a2分别表示卫星在参考时刻t0时的钟差、钟速和钟速变化率；e为n维误差向量。可得最小二乘解

普通最小二乘解算卫星钟差模型参数时，采用单位阵作为观测值权矩阵，即将新老钟差观测数据统一对待，但对于预报而言，离预报时刻越近的观测数据与后续预报结果的相关性越强，对预报钟差的贡献也越大。因此，在解算钟差模型参数时，把单位阵当作观测值权矩阵是不合理的[8］。为了离预报时刻越近的观测数据对预报模型的贡献，削弱老数据的影响，可以引入遗忘因子矩阵作为观测权矩阵。取遗忘因子不同的值就可以得到不同的遗忘效果[8］。若已知遗忘因子为λ，则遗忘因子矩阵W

在采用以前的全部观测数据进行卫星钟差的预报卫星钟差，随着观测数据时间的增加，会造成数据饱和，降低参数估计的速度和效率，显然不能用以前所有的全部观测量进行卫星钟差的预报，可以采用实时更新的固定的一定长度的钟差数据对卫星钟差进行拟合预报。

1.2 卫星钟差完好性监测算法步骤

卫星钟的完好性监测主要是监测卫星钟差异常，其具体步骤如下

1）建立卫星钟差模型，利用实时更新的一定长度的钟差数据实时预报卫星钟差。在卫星钟异常监测算法中，实时更新的数据长度是很重要的，数据长度决定了预报钟差的精度，长度越大预报钟差精度越高，处理器负担也越大，影响系统的实时性，在实际处理中固定数据长度可以在20～100之间取值。

2）计算统计检验量及监测门限，判断是否发生异常。

若利用参考站网络实时解算出的卫星钟差为x（n）solve，预报钟差为x（n）pre，则可构造统计监测量z（n＋1）为

已知实时解算钟差标准偏差σsolve、预报钟差的标准偏差σpre，根据方程（5），利用协方差传播定律可得z的方差结果：

3）如果钟差数据没有发生异常，则利用正常结算得到的钟差数据，实时更新卫星钟差预报模型；若钟差数据发生异常，则对钟差异常数据进行剔除，并利用实时输出的预报钟差代替异常值对钟差预报模型进行更新，预报下一历元，从而完成异常数据的替换。

2 实验分析

为了能够更好的验证文中算法的监测效果，采用IGS网站提供的事后精密卫星钟差产品进行实验分析，数据为2012年1月27日采样间隔为30s的数据。根据表1随机选取不同类型的四颗卫星进行试验分析，这四颗星分别是8号Block IIA铯钟、17号Block IIR－M铷钟、18号Block IIR铷钟及26号Block IIA铷钟。设计了两种试验方案进行卫星钟完好性监测分析，两种方案均利用实时更新的长度一定的钟差数据实时预报卫星钟差，进而实现卫星钟差的异常监测，均固定实时更新数据的长度为100.其中，方案一采用最小二乘算法（LS），方案二采用遗忘因子最小二乘算法（FFLS）。

2.1 卫星钟差预报性能分析

由卫星钟差异常监测原理可知，卫星钟差异常监测的能力与卫星钟差的预报精度有很大关系，图1～图4分别给出了采用不同方法对8、17、18和26四颗卫星的钟差预报误差图，表1示出了两种方案对四颗卫星钟差的预报精度。

图1 8号卫星钟差预报误差

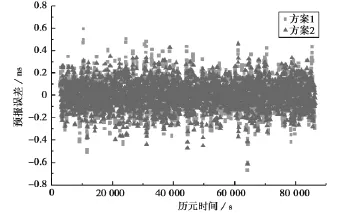
图2 17号卫星钟差预报误差

图3 18号卫星钟差预报误差

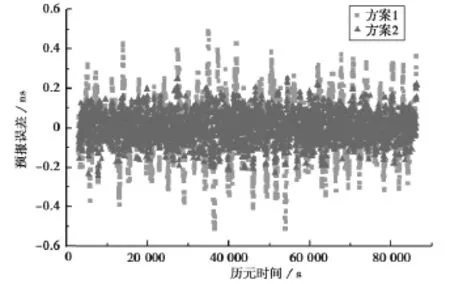
图4 26号卫星钟差预报误差

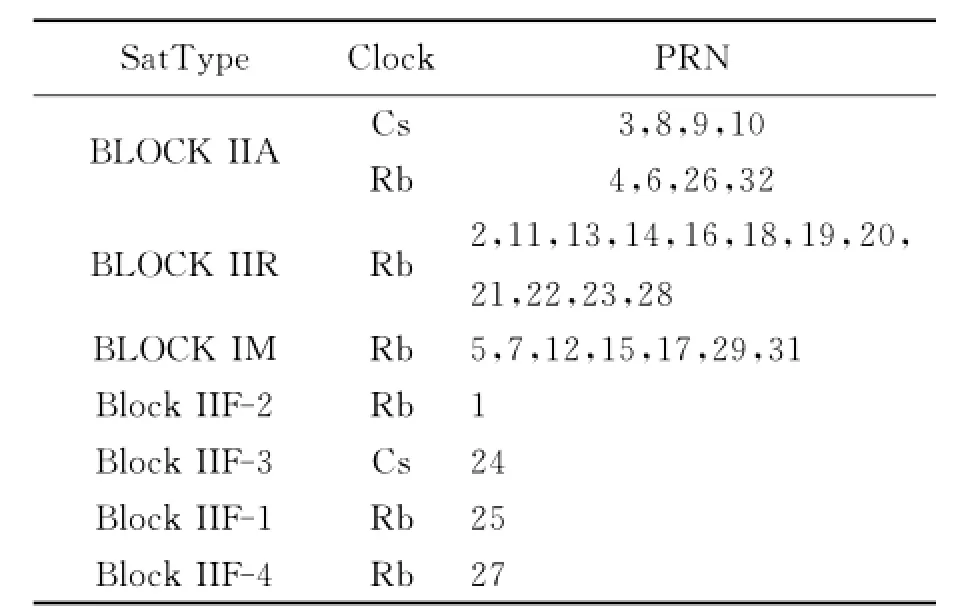
表1 GPS卫星钟类型和卫星号对照表

采用相同算法预报的不同卫星钟差的精度并不相同，通常情况下，原子钟越稳定预报效果越好，但由图1～图4和表2可知，采用最小二乘算法时，原子钟性能较好的17号和18号卫星的预报精度与稳定性较差的26号卫星预报精度基本相当，采用遗忘因子最小二乘算法时，稳定性较差的26号星的预报精度反而好于稳定性较好的17号和18号卫星，这主要是因为在这种小样本的超短期钟差预报中，预报钟差的精度虽与卫星钟的稳定性有关，但更主要的是取决于卫星钟钟差在该时段内的小尺度变化[9－10］。对同一卫星而言，FFLS算法具有波动相对较小的特点，对卫星钟差的预报精度优于LS算法。采用FFLS算法分别可以将四颗卫星的钟差预报精度从0.46ns、0.15ns、0.14ns、0.15ns分别提高到0.21ns、0.12ns、0.12ns、0.07ns，尤其是对于对8号和26卫星的钟差预报精度提高较为明显，考虑到这两颗卫星分别为已经工作了20多年的Block IIA铯钟和Block IIA铷钟，原子钟的稳定性相对较低，因此可以得出结论卫星钟稳定性越差，采用FFLS算法对钟差预报精度提高越明显，越能体现出FFLS算法的优越性。

表2 三方案钟差预报精度RMS（单位：ns）

2.2 卫星钟差异常监测性能分析

为了能更好的验证算法的监测效果，本文通过对IGS事后精密钟差数据加入异常数据模拟异常发生的情况，对算法进行验证和分析。误警概率取为1/15 000，计算一天数据，统计能够准确探测出异常的百分比。图5示出了8、17、18和26四颗卫星采用两种方法探测出钟差异常的成功率随加入的钟差异常值大小的曲线变化。

图5 钟差异常探测成功率曲线

从图5可以看出，钟差异常检测成功率随着加入钟差异常值的增大而增大。当探测成功率达到99%时，采用LS算法，8、17、18和26四颗卫星能探测出的最小钟差异常分别为2.265、0.650、0.900、0.950；采用FFLS算法，四颗卫星能探测出的最小钟差异常分别为1.225、0.550、0.775、0.575.显然，对于同一颗卫星，FFLS算法的异常监测能力明显高于LS算法，尤其是对卫星钟稳定性越差8号卫星，探测能力提高的更为明显，能够将检测出的钟差异常从2.265ns提高到1.225ns.

3 结束语

卫星钟差精度直接影响高精度用户的定位结果，实时定位系统中，在提供实时精密卫星钟差产品的同时，还应当实时提供钟差完好性信息，因此应当对卫星钟差异常进行实时监测。本文基于钟差预报值实现了卫星钟差的完好性算法，在钟差拟合预报模型基础上，实时得到卫星钟差预报值，将实时解算的卫星钟差与预报钟差比较，来实时对卫星钟差异常进行监测，试验结果表明：FFLS算法钟差预报精度和钟差完好性监测能力均明显高于LS算法，并且FFLS算法方法简便易行，应用灵活，比较适用于卫星钟差完好性的实时监测。

[1]方书山.GPS卫星钟差完备性监测研究与算法实现[D］.阜新：辽宁工程技术大学，2011：19－35.

[2]唐 升，刘 娅，李孝辉.星载原子钟自主完好性监测方法研究[J］.宇航学报，2013，34（1）：39－45.

[3]牛 飞，韩春好，张义生，等.导航卫星星载原子钟异常监测分析[J］.武汉大学学报·信息科学版，2009，34（5）：585－588.

[4]RODRIGUEZ I，GARCFA C，CATALAN C，et al.Satellite autonomous integrity monitoring（SAIM）for GNSS systems[C］//ION GNSS 2009，2009.

[5]黄新明，龚 航，朱祥维，等.基于Kalman滤波器的卫星钟实时异常监测算法[J］.宇航计测技术，2011，31（5）：6－11.

[6]许龙霞，李孝辉.基于接收机钟差的GPS完好性自主检测算法[J］.宇航学报，2011，32（3）：537－542.

[7]黄观文.GNSS星载原子钟质量评价及精密钟差算法研究[D］.西安：长安大学，2012.

[8]宋 成，王雪飞，庄钊文.基于遗忘因子最小二乘的GPS接收机钟差预测算法研究[J］.测绘科学，2008（s1）：41－43.

[9]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D］.郑州：信息工程大学，2006：143－161.

[10]于合理，郝金明，刘伟平，等.卫星钟差超短期预报模型分析[J］.大地测量与地球动力学，2014，34（1）：161－164.

Real－Time Integrity Monitoring Algorithm of Satellite Clock Based on Prediction

WU Chuanlong1，CHEN Shen1，ZHANG Haitao1，LIU Meng2
（1.61175 Troops of PLA，Wuchang430000，China；2.61243 Troops of PLA，Lanzhou730000，China）

The model of satellite clock error was established based on historical data，a real－time integrity monitoring algorithm of satellite clock was proposed，and comparative analysis the effect of integrity monitoring by using the least squares algorithm and forgetting factor least squares algorithm.The results showed that：forgetting factor least squares algorithm is better than the least－squares algorithm to monitor.

Satellite clock error；integrity；real－time monitoring；the forgetting factor least square algorithm

P228.4

A

1008－9268（2015）01－0023－04

10.13442/j.gnss.1008－9268.2015.01.005

吴传龙（1987－），男，湖北天门人，助理工程师，主要从事大地测量和卫星导航定位研究。

陈 慎（1986－），男，湖北应城人，助理工程师，主要从事大地测量和卫星导航定位研究。

张海涛（1986－），男，湖南澧县人，助理工程师，主要从事大地测量和卫星导航定位研究。

刘 梦（1978－），女，山东莱芜人，工程师，主要从事测量数据处理和地图编绘工作。

2014－11－03

联系人：吴传龙E－mail：wuchuanlong1987＠163.com