周跳对GNSS 精密定位的影响

夏思琦，于先文

（东南大学 交通学院，南京 211189）

0 引言

载波相位是全球卫星导航系统（global navigation satellite system, GNSS）精密定位中1 个必不可少的观测值。在对载波相位的观测过程中，由于外界干扰或者硬件故障等原因，会造成接收机整周计数器发生中断，从而导致载波相位观测值发生整周跳变，这个整周跳变被称作周跳。周跳具有传递性，一旦在某个历元发生了周跳，此历元之后的所有载波相位观测值中均会含有该周跳。周跳是1 种常见现象，特别是当观测环境较差时，周跳的发生会更加频繁。

随着GNSS 定位技术应用领域和工作环境的日益拓展，须不断完善GNSS 精密定位数据处理方法，其中周跳的探测与修复是1 个非常重要的环节。目前已提出了多种周跳探测与修复方法，主要有高次差法[1]、多普勒观测值法[2-3]、图尔博·埃迪特（TurboEdit）方法[4-5]、3 频组合周跳探测法[6-7]等。但周跳被误探、漏探的情况仍时有发生，导致GNSS 定位结果受到较大的影响。文献[8]指出，周跳对于GNSS 定位的影响是不能被忽略的问题，即使观测值中只含有1 个周跳，也会对定位结果造成分米级的影响；文献[9]以全球定位系统（global positioning system,GPS）3 差模型为基本参数模型，讨论了周跳对基线向量的影响，但未对影响程度进行分析；文献[10]提出，当观测数据中含有周跳时，对相对定位中的双差解会造成很大的影响，但也未给出具体的影响程度。

目前，GNSS 定位技术的应用越来越广泛，在一些特殊环境下（城市街道、高边坡路等）进行定位时，受多路径等因素影响，导致周跳的发生会变得更加频繁[11]。因此，研究周跳对定位的影响机理与程度，对完善数据处理方法具有一定的参考价值。

1 GNSS 精密定位模型

当某一历元无周跳发生时，原始载波相位观测方程[12]可写成

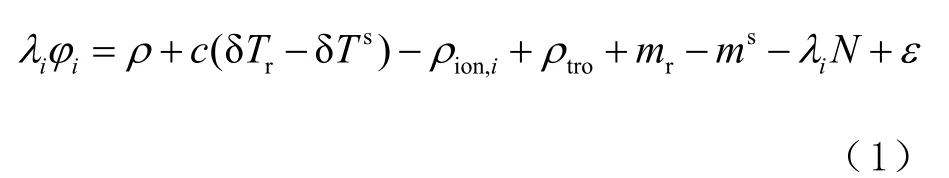
式中：iλ 为第i 个频率载波相位观测值φ 的波长；ρ 为星地间的几何距离；ρion,i为第i 个频率载波相位观测值φ 对应的电离层延迟；ρtro为对流层延迟； δTr、δTs分别为接收机r 和卫星s 的钟差；c 为真空光速；mr、ms分别为接收机r 和卫星s的相位硬件延迟；N 为整周模糊度；ε 为观测随机误差。

式（1）中的未知参数包括模糊度、坐标（或基线）向量，其中模糊度具有整数特性。当有多个载波观测值时，基于式（1）可得的观测方程为

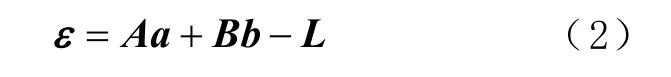
式中：L为载波观测值与各模型化的系统误差之和构成的矩阵；a 为模糊度向量；b 为坐标（或基线）向量；A 和B 为已知系数矩阵；ε 为观测随机误差向量。

对式（2）进行加权最小二乘估计[13]，得到未知参数a 和b 的实数解向量为

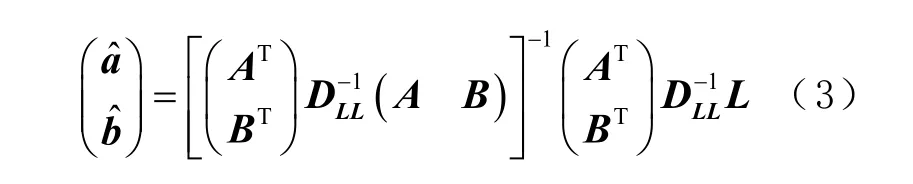
相应的方差阵为

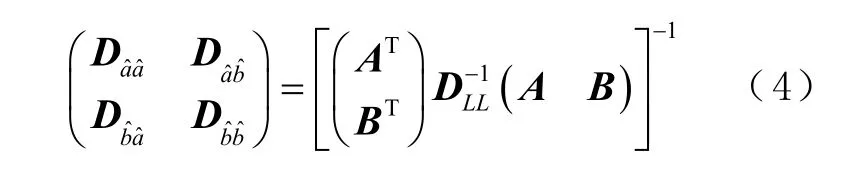
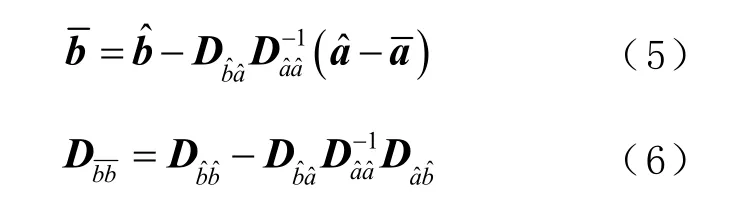
由式（6）可知，当模糊度被固定后，b 的整数解较实数解在精度方面会有很大的提高。

2 周跳的影响

2.1 周跳对实数解的影响

当有周跳发生时，式（2）可写成

式中ΔN 为周跳向量。

同样地，对式（7）进行加权最小二乘估计，得到未知参数a 和b 的实数解

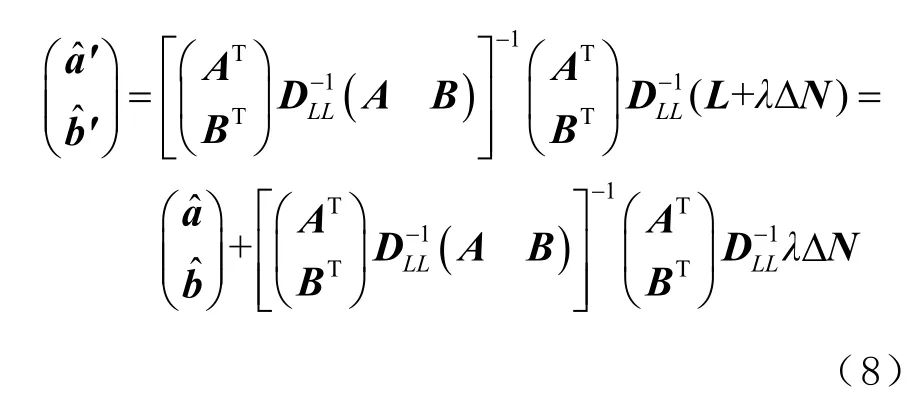
对式（8）中的逆矩阵进行展开，可得

由式（9）可知，周跳对定位实数解带来的系统误差

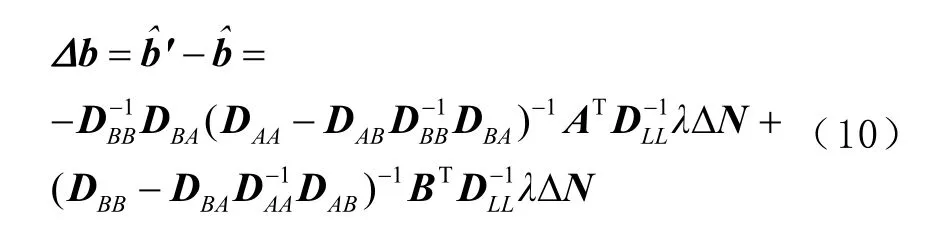
式中Δb 为周跳对定位实数解带来的系统误差。

式（10）中不含随机误差项，故Δb 是1 个固定向量。基于式（9），可得的均方差阵

由式（11）可知，有周跳发生时定位实数解的精确度要差于无周跳发生时定位实数解的精确度，其精度损失可表示为

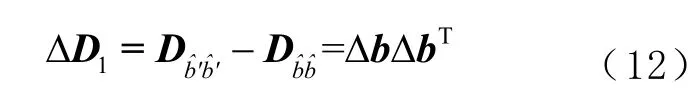
式中Δ1D 为周跳对定位实数解所造成的精度损失。

为了更直观地反映周跳对定位实数解精度的影响，将方矩阵Δ1D 映射成1 个值，得到定位实数解精度损失指标

式中： tr (· )为方阵的迹；Δs 为周跳对定位实数解所造成的精度损失指标。

利用式（13）即可计算出周跳对定位实数解所造成的精度损失。

2.2 周跳对整数解的影响

当没有周跳发生时，b 的整数解向量及相应方差阵如式（5）和式（6）所示。当周跳发生后，原来已固定的模糊度由于受到周跳影响将不能被固定，因此不能获得定位整数解，定位结果为受污染的实数解。此时周跳对定位整数解带来的系统偏差可表示为

式中Δb′ 为周跳对定位整数解带来的系统偏差。

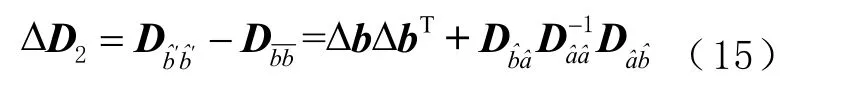
式中Δ2D 为周跳对定位整数解所造成的精度损失。

由式（15）可知，Δ2D 与具体观测值无关且恒为正定矩阵。因此，当观测值中含有周跳且导致模糊度无法被固定时，会对定位结果产生严重影响，直到模糊度再次被固定后，这种影响才会消失。

为了更方便地反映周跳对定位整数解精度的影响，将方矩阵Δ2D 映射成1 个值，可得精度损失指标

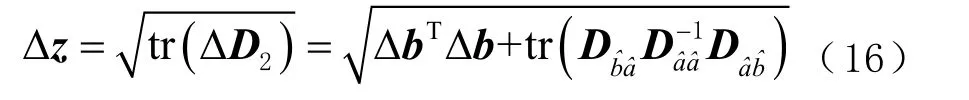
式中Δz 为周跳对定位整数解所造成的精度损失指标。

3 实验与结果分析

3.1 实验数据

本算例采用的实验数据来源于2018 年1 月16日，南京1 条18 km 左右的基线，测站名分别为MAQN 和JNNF。接收机型号为Trimble NetR9，采样间隔1 s，卫星截止高度角设为15°。利用2 个观测站长期连续观测数据解算得到该基线向量准确值，并将该准确值作为向量坐标真值。利用定位软件对该组数据进行相对定位解算，将获得的基线向量整数解坐标与向量坐标真值作差，得到的坐标真误差情况如图1 所示。

从图1 可以看出，3 个方向的误差变化整体平缓且坐标真误差均在0.005 m 附近波动。说明该组数据中无周跳发生。因此采用该组无周跳的观测数据分别进行小周跳、大周跳、连续周跳对定位影响的实验。

图1 无周跳时定位结果

3.2 小周跳的影响

为了分析小周跳对定位的影响程度。在MAQN 观测站的第5 个历元处，G05 号卫星L1 频点上的载波相位观测值中加入1 个周跳，由于周跳的继承性，之后L1 所有历元的载波相位观测值中都将包含1 个周跳。利用定位软件重新对该条基线数据进行相对定位解算，获得的G05 号卫星L1 频点上的整周模糊度情况如图2 所示。

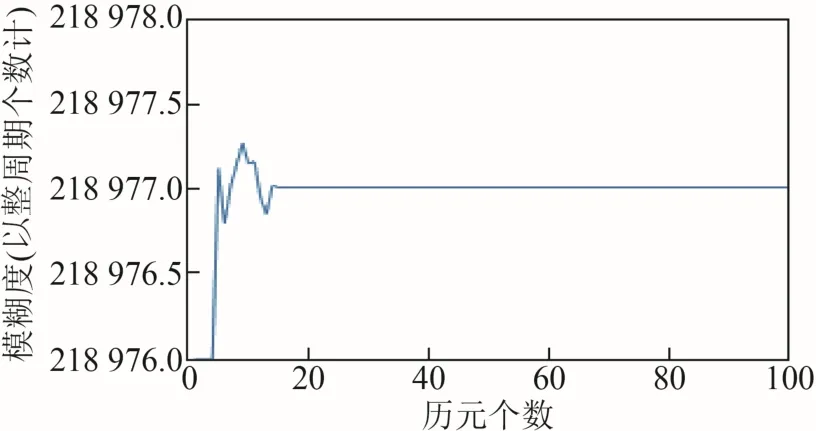
图2 模糊度变化情况（1 个周跳）

从图2 中可以看出，在加入周跳前，模糊度的整数解为218 976 个周期，加入1 个周跳后的一段时间内，模糊度变为了实数解，在218 977 个周期附近震荡，说明随着历元的增加，周跳逐渐被吸收至模糊度中。从第15 个历元开始，模糊度才重新被固定。

将利用软件解算得到的基线向量与向量坐标真值作差，结果如图3 所示。从图3 中可以看出，在第5 个历元处的东（E）、北（N）、天（U）方向坐标真误差在0.15 m 左右。而从第15 个历元开始，模糊度重新被固定，E、N、U 方向的坐标真误差也回到0.005 m 附近波动。

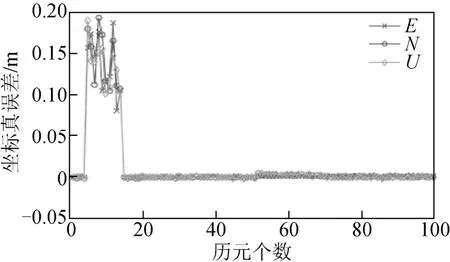
图3 加入周跳后定位结果

表1 为在第5～14 个历元，基于式（16）计算各历元的精度损失指标 Δz 。

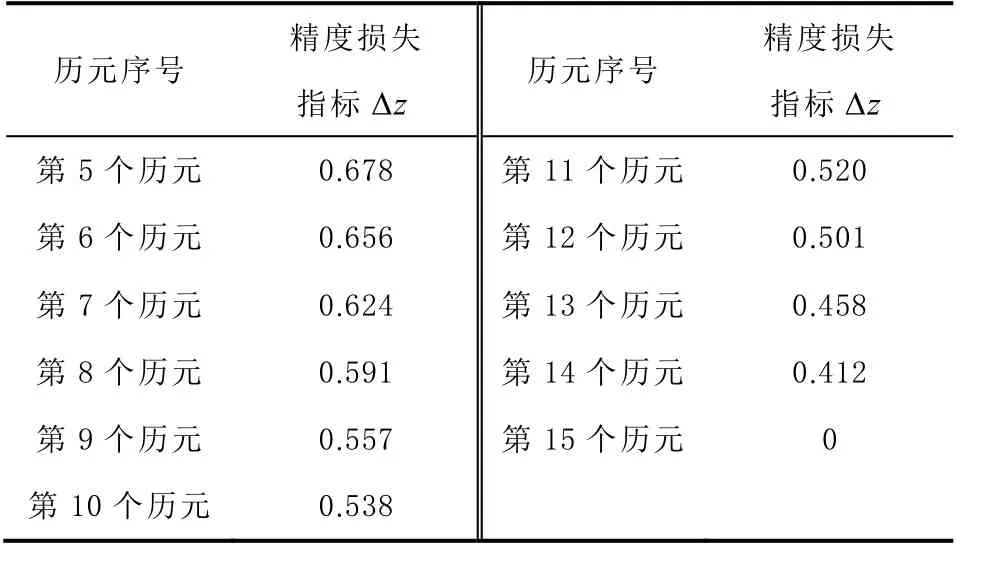
表1 第5～15 个历元精度损失指标

由表1 可知，在第5 个历元处， Δz 达到了0.678 m，可知周跳对定位会产生较大的影响。随着历元的增加逐渐减小，直到第15 个历元模糊度被重新固定后， Δz 变为0 m。

3.3 大周跳影响

为了分析大周跳对定位的影响程度，同样在MAQN 观测站的第5 个历元处，G05 号卫星L1频点上的载波相位观测值中产生了10 个周跳，由于周跳的继承性，之后L1 所有历元的载波相位观测值中都将包含10 个周跳。利用定位软件重新对该条基线数据进行相对定位解算，获得的G05 号卫星L1 频点上的整周模糊度情况如图4所示。

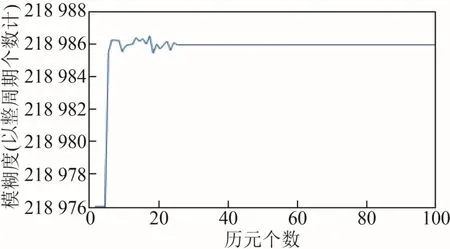
图4 模糊度变化情况（10 个周跳）

从图4 中可以看出，在加入周跳前，模糊度的整数解依旧为218 976 个周期，加入周跳后一段时间内，模糊度不能被固定，直至第25 个历元，模糊度才重新被固定。

将利用软件解算得到的基线向量与向量坐标真值作差，结果如图5 所示。从图5 中可以看出，在第5 个历元处的E、N、U 方向坐标真误差在1～2 m。而从第25 个历元开始，模糊度重新被固定，E、N、U 方向的坐标真误差也回到0.005 m附近波动。

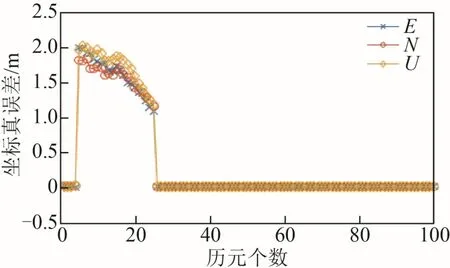
图5 加入周跳后定位结果

用第5～26 个历元处的数据，基于式（16）计算处各历元的精度损失指标 Δz ，其结果如表2所示。

表2 第5～26 个历元精度损失指标

由表2 可知，在第5 个历元处，Δ z 达到了3.278 m，可知周跳对定位会产生较大的影响。随着历元的增加逐渐减小，直到第26 个历元模糊度被重新固定后， Δz 变为0 m。

3.4 连续周跳对定位影响

为了分析连续周跳对定位的影响程度，在MAQN 测站的第5 个、第8 个历元处，G05 号卫星L1 频点上的载波相位观测值中分别产生了1 个周跳。利用定位软件重新对该条基线数据进行相对定位解算，获得的G05 号卫星L1 频点上的整周模糊度情况如图6 所示。

从图6 中可以看出，在加入周跳前，模糊度的整数解依旧为218 976 个周期，在第5 个历元加入周跳后，模糊度不能被固定。在第8 个历元加入周跳后，模糊度进一步受到影响，仍不能被固定。直至第18 个历元，模糊度才重新被固定。

将利用软件解算得到的基线向量与向量坐标真值作差结果如图7 所示。

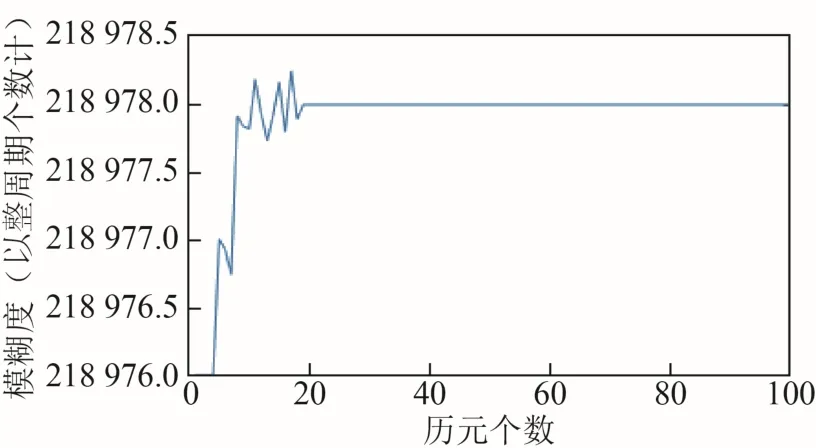
图6 模糊度变化情况（连续周跳）

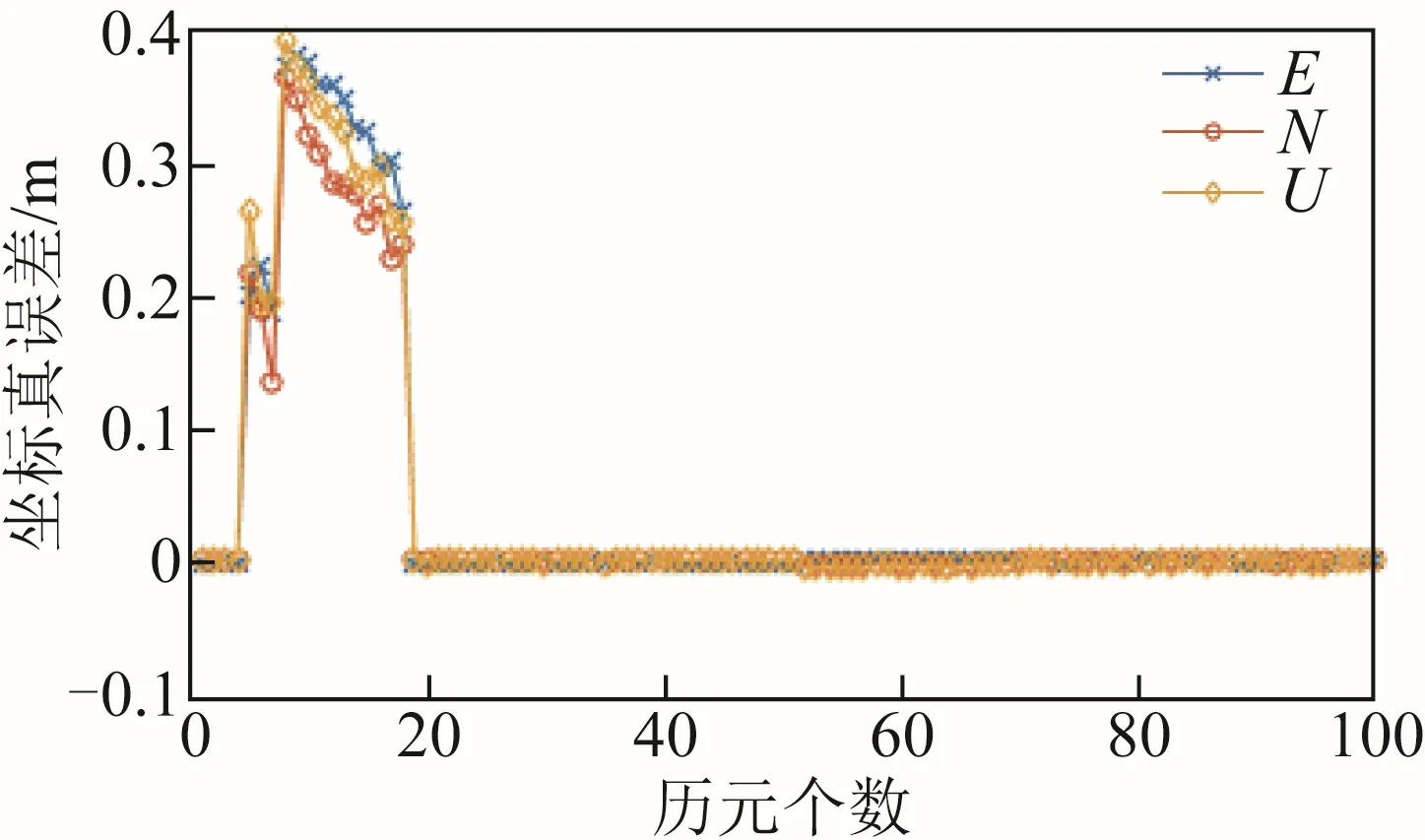
图7 加入周跳后定位结果

从图7 中可以看出，在第5 个历元处的E、N、U 方向坐标真误差在0.2 m 左右。随着历元的增加，周跳逐渐被吸收至模糊度中，坐标真误差逐渐减小。由于在第8 个历元处又有了1 个周跳的产生，E、N、U 方向坐标真误差重新达到了0.3 m 左右。随着历元的增加，坐标真误差继续逐渐减小，从第19 个历元开始，E、N、U 方向的坐标真误差也回到0.005 m 附近波动。

利用第5～19 个历元的观测数据，基于式（16）计算出各历元的精度损失指标 Δz ，其结果如表3 所示。

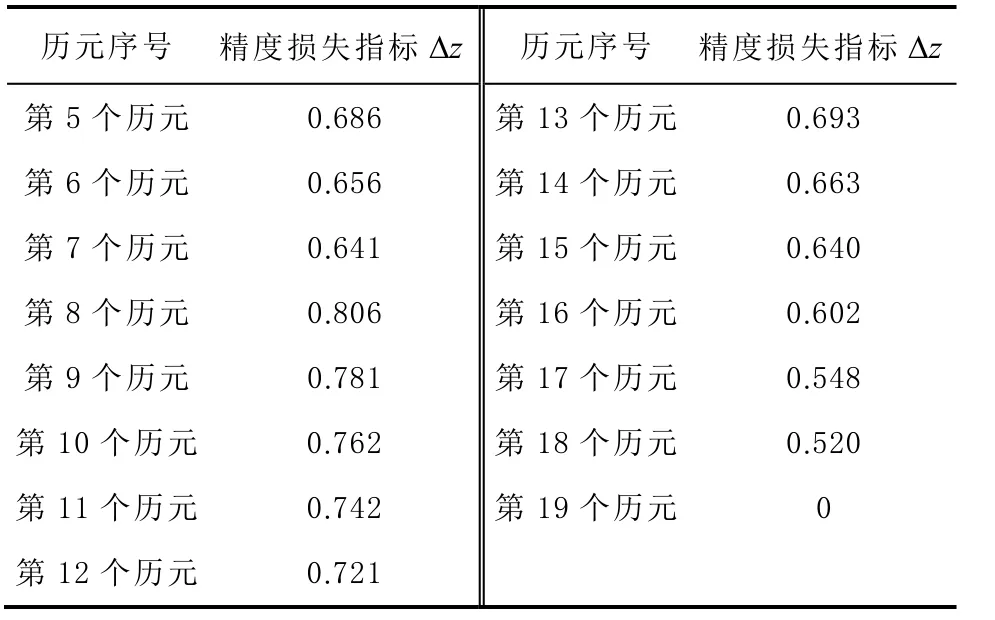
表3 第5～19 个历元精度损失指标

由表3 可知，在第3 个历元处， Δz 达到了0.686 m，之后随着历元的增加逐渐减小，由于在第8 个历元处重新出现了1 个周跳， Δz 又重新达到了0.806 m，之后再次随着历元的增加逐渐减小，直到第19 个历元模糊度被重新固定后，Δ z 变为0 m。

4 结束语

本文首先给出了GNSS 精密定位模型；然后推导了周跳对定位实数解和定位整数解的影响程度计算公式，并根据方差阵分析了相应的精度损失；最后通过对人为加入大、小、连续周跳到观测数据中，重新进行定位解算，将得到定位结果与无周跳观测数据的定位结果相互之间进行对比，可得到如下结论：①周跳发生之后，模糊度被重新固定所需的历元个数与周跳的大小有关，一般周跳值越大，模糊度重新固定所需的历元个数越多；②当发生连续周跳时，对定位的影响程度会出现叠加现象，模糊度被重新固定所需的历元个数将会增多。