两种卫星导航抗干扰算法对载波相位测量精度影响分析

居后鸿，曾庆化，岳亚洲，张会锁，寇 磊

（1.南京航空航天大学自动化学院导航研究中心，江苏南京210016；2.中航工业西安飞行自动控制研究所，陕西西安710065）

两种卫星导航抗干扰算法对载波相位测量精度影响分析

居后鸿1，2，曾庆化1，岳亚洲2，张会锁2，寇 磊2

（1.南京航空航天大学自动化学院导航研究中心，江苏南京210016；2.中航工业西安飞行自动控制研究所，陕西西安710065）

PI算法与LCMV算法是被深入研究与广泛应用的两种抗干扰算法，若信号经过两种算法处理后产生相延迟，则会给载波相位的测量带来误差，从而影响载波相位差分精度。简要介绍了相延迟以及PI算法与LCMV算法，并通过算法公式分析得出PI算法会随干扰输入信号和卫星信号方向的变化而变化，而LCMV算法则不会因输入信号和卫星信号的变化产生相延迟。利用MATLAB仿真平台，仿真出干扰环境下PI算法与LCMV算法产生的相延迟，通过仿真结果分析验证两种算法对于载波相位测量精度的影响。

星导航；载波相位；相延迟；PI算法；LCMV算法

0 引 言

在GPS系统中，载波相位是一种重要的观测量。由于载波波长与测距码的码元长度相比要短得多，通过载波相位差分的定位精度可以达到厘米级甚至毫米级，比伪距定位精度高1～2个数量级。因此，提高载波相位测量质量对于提高卫星导航定位精度具有重要的意义，对导致载波相位测量产生误差的因素进行分析和研究也是有必要的[1－3］。

卫星信号从发送到被接收机终端接收，可能受到各种人为或者环境的干扰，所以提高卫星导航系统的抗干扰能力十分重要。天线阵列与各种抗干扰算法相结合是一种被广泛采用的卫星导航抗干扰手段。由于信号经过抗干扰系统产生的相延迟是载波相位测量误差的来源之一，抗干扰处理过程若是使得载波相位测量的质量降低，则最终会影响载波相位差分的精度[4－5］。PI算法与LCMV算法是两种被深入研究与广泛应用的抗干扰算法，通过仿真分析比较两种算法产生相延迟的大小，可以分析研究这两种算法对于载波相位测量精度的影响。

1 相延迟与抗干扰算法

1.1 相延迟

为了在干扰环境中接收卫星信号，必须要在接收端降低干扰对于卫星信号的影响，一种应用广泛的抗干扰手段是阵列天线与抗干扰算法处理相结合。输入信号经过抗干扰系统产生的相延迟可能会降低伪载波相位测量的质量，影响载波相位差分的精度。在对导航精度有着严格要求的情况下，为了进一步追求卫星导航定位的精度，必须要考虑抗干扰算法的相延迟情况。

需要说明的是，在实际情况下，相延迟还会受到阵元互耦、天线增益/相位失配、天线相位中心误差、射频前端、温度以及多路径效应等诸多因素的影响[6］。

1.2 PI算法

在大多数情况下，预先获知干扰信号的数目与形式存在难度。卫星信号功率比较小，远小于内热噪声。在这种情况下，采用PI算法较合适[7］。

PI算法（又称功率倒置算法）以阵列输出功率最小作为最优化准则，通过调节各个阵元的加权系数，使最后抗干扰系统输出信号功率最小，且干扰功率越强，对应的干扰方向生成的零陷越深。可表示为

式中：Rx为输入信号协方差阵；δ＝[1，0，…，0］T.利用拉格朗日算子可得最优权值：

1.3 LCMV算法

LCMV算法由Frost于1972年提出，简称Frost波束形成器，又称最小方差无失真响应的自适应波束形成器。LCMV算法是对加权矢量施加线性约束条件，以便有效地控制波束响应，使得从期望方向来的信号能以特定的增益与相位通过[8－9］。

设波束形成器对于方向为θ的信号响应由下式得到

式中，a（θ）为信号引导矢量。将上式中加权矢量w的约束设置为

通过这样的方式，可以保证任何方向为θ的信号都能以增益1通过。对于输出功率中干扰分量的最小化，可以通过加权矢量的选择，使得输出功率的期望值取最小值。LCMV问题可表示为

利用拉格朗日算子可得

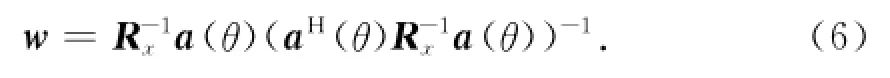
1.4 两种算法对相延迟的影响

设卫星信号s（t），则期望信号经过抗干扰系统后的输出为

式中：o（t）为输出；wH为天线阵列权值；a（θ）为期望信号的引导矢量。对于PI算法，将公式（2）代入公式（7）有：

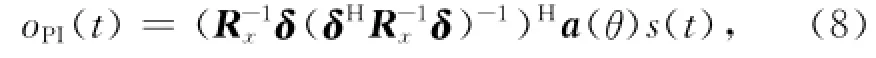
式中：R为输入信号协方差阵；δ＝[1，0，…，0］T.

在实际中，卫星期望信号很小，故输入信号可以看作只包含干扰信号和噪声。从式（8）容易看出，卫星期望信号经过PI算法输出oPI（t）要受到卫星信号引导矢量a（θ）与输入信号协方差阵Rx的共同影响。在输入信号一定的情况下，oPI的相位会因卫星信号方向的变化而变化。

对于LCMV算法，将式（5）中第二个公式代入式（7）有

式（9）说明，卫星信号经过LCMV算法输出oLCMV（t）仍然是原卫星信号，其相位不会因卫星信号方向的变化而变化。

从式（9）中的输出oLCMV看，LCMV算法不仅对固定方向的信号响应约束在一定的幅值，而且约束在一定的相位。对比式（8）和式（9），可以看出PI算法的输出会受到卫星信号方向和输入信号的共同影响，不能对固定方向的信号进行约束，输出信号的相位会因卫星信号方向的变化和输入信号的变化而发生改变。从相延迟的角度考虑，LCMV算法要优于PI算法，这在后面的仿真实现中可以得到验证。

2 仿真结果与分析

仿真采用4阵元Y阵；阵列输入信号为一个单频窄带干扰信号与高斯白噪声，干噪比50dB，初相为0，方向为[10°20°］（俯仰角，方位角）。最后仿真得到信号响应r（θ）的相角（信号输出的相延迟）。图1示出了PI算法与LCMV算法在相同干扰环境下的相延迟。

从图1可以看出，PI算法随信号方向的变化，产生的相延迟也发生变化；LCMV算法的相延迟并不随信号方向的变化而变化，且相延迟很小。这是因为LCMV算法能够约束特定频率方向上的信号，也就约束着抗干扰系统输出信号的相位；但是PI算法并不具备这样的功能，使得输出信号相位不稳定，甚至会产生很大的相延迟。

在LCMV算法相延迟图中的峰值点，产生在干扰方向[10°20°］上。由于此时信号方向与干扰方向相同，产生了相对比较高的相延迟，这也符合实际当中的干扰情况。

为了更进一步研究验证PI算法和LCMV算法的相延迟，采用另一种步骤进行仿真：

1）仿真生成一个卫星期望信号s作为输入信号，简化起见，卫星信号设置为正弦信号（幅值为1，初相为0）。

2）仿真生成干扰环境，将卫星期望信号到达天线阵列的方向设置为[17°76°］[53°23°］、[84°134°］、[21°43°］、[46°10°］，并据此得到引导矢量a（θ）.

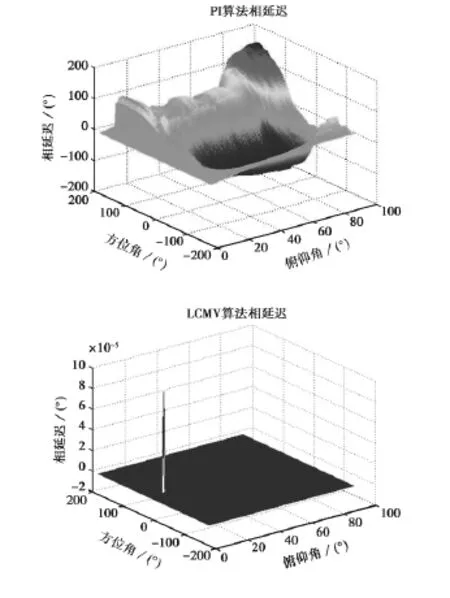
图1 PI算法与LCMV算法相延迟

3）在具有干扰与卫星信号的环境下，根据PI算法与LCMV算法得到对应两组权值w1与w2.

4）将w1与w2分别代入公式（7）中，得到期望信号经过PI算法和LCMV算法处理后的输出。

5）作出输出o（θ）的时域图。

这里需要说明的是，由于考虑算法对于相位的影响，只是研究不同方向卫星信号的相位是否相同，所以对于输出信号的幅值统一化为1，最后的结果如图2所示。

从图2的PI算法输出时域图可以看出，每个方向上输出的相位与其它方向的相比都不一样。对于LCMV算法，各个方向上的输出相位都是相同的，不会随卫星信号方向的不同而变化。

仿真结果表明：从相延迟的角度考虑，LCMV算法由于可以对特定信号进行约束，采用LCMV算法输出的信号相延迟很小，对于载波相位的影响也是很小。PI算法产生的相延迟随信号方向的变化而变化，且有时会产生较大的相延迟。所以采用LCMV算法能比PI算法获得更好的载波相位精度。

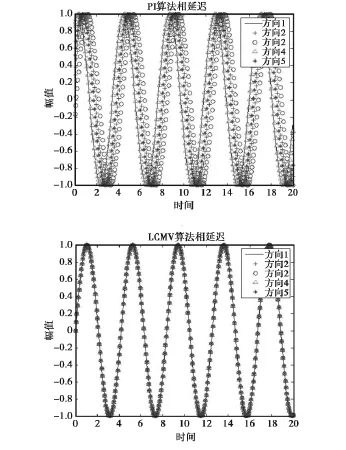
图2 PI算法与LCMV算法输出信号时域图

3 结束语

卫星导航抗干扰问题越来越受到重视，天线阵列与抗干扰算法相结合抑制干扰信号的方法被广泛采用。由于抗干扰处理过程中可能会使系统输出产生一定的相延迟，会给载波相位的测量带来一定的误差，对于载波相位差分的精度有一定的影响，所以对其进行分析是十分必要的。本文对两种常用的抗干扰算法——PI算法与LCMV算法，以及相延迟进行简要的介绍通过算法公式分析得出在输入信号一定的情况下PI算法相延迟会随着卫星期望信号方向的变化而变化，而LCMV算法则不会产生相延迟。通过MATLAB仿真平台，仿真出在干扰环境下PI算法与LCMV算法的相延迟，分析验证了两种算法对于载波相位测量精度的影响。仿真结果验证了之前的分析结论，从载波相位测量精度的角度考虑，LCMV算法要优于PI算法。

[1]李小民，田庆民.适应高动态环境的GPS载波相位估计方法研究[J］.武汉大学学报，2003，36（3）：120－124.

[2]岳 淼.GPS载波相位高精度惯性组合导航系统研究[D］.南京：南京航空航天大学，2007.

[3]党亚民.高精度DGPS测量中的载波相位改正[J］.测绘科技动态，1994（4）：19－23.

[4]MCGRAW G A，MCDOWELL C，KELLY J M.GPS anti－jam antenna system measurement error characterization and compensation[C］//19th International Technical Meeting of the Satellite Division of The Institute of Navigation，2006.ION，2001：705－714.

[5]ORR A，DE LORENEO D，KIM U S，et al.Phase effects analysis of patch antenna CRPAs for JPALS[C］//ION 2004，Institute of Navigation，Long Beach，CA Sept 21－24，2004：1531－1538.

[6]ANANTHARAMU P B，BORIO D，LACHAPELLE G.Self－contained GNSS－based antenna array calibration[C］//2011International Technical Meeting of The Institute of Navigation.ION，2011：1232－1239.

[7]MOHAMED E A，王永芳，谈展中.用于GPS接收机的自适应算法抗干扰性能比较[J］.北京航空航天大学学报，2006，32（5）：561－565.

[8]苗剑峰，抗差自适应GPS软件接收机的关键技术研究[D］.南京：南京航空航天大学，2009年.

[9]叶建杰.一种应用于GPS抗干扰的改进LCMV算法[J］.电子科技，2013，26（2）：156－158.

Analysis of Carrier Phase Measurement Accuracy of Two Satellite Navigation Anti－jam Algorithms

JU Houhong1，2，ZENG Qinghua1，YUE Yazhou2，ZHANG Huisuo2，KOU Lei2
（1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing210016，China；2.AVIC Xi′an Flight Automatic Control Research Institute，Xi′an 710000，China）

PI algorithm and LCMV algorithm are two deeply studied and widely used anti－jam algorithms.If phase delay emerges after signals are processed by the two algorithms，it will bring carrier phase measurement error，which will affect carrier phase difference accuracy.This paper introduces phase delay and PI/LCMV algorithms briefly，and，by analyzing algorithm expressions，reaches a conclusion that phase delay of PI algorithm will change when input signal and satellite signal direction change，while LCMV algorithm will not bring phase delay with the presence of signal changes.It simulates phase delay of PI algorithm and LCMV algorithm under jamming environment through MATLAB，verifies and analyzes the effects of the carrier phase measurement accuracy using the two algorithms.

Satellite navigation；carrier phase；phase delay；PI algorithm；LCMV algorithm

P228.4

A

1008－9268（2015）01－0013－04

10.13442/j.gnss.1008－9268.2015.01.003

居后鸿（1989－），男，硕士生，研究方向为卫星导航技术。

曾庆化（1979－），男，博士，副教授，研究方向为惯性/卫星/视觉/图像匹配/无线传感器组合导航。

岳亚洲（1971－），男，博士，研究员，研究方向为高精度惯导与组合导航。

张会锁（1970－），男，硕士，高工，研究方向为卫星导航技术。

寇 磊（1981－），女，高工，研究方向为卫星导航技术。

2014－10－30

国家自然科学基金（批准号：61374115，61328301，61104188，61273057，61174197）；江苏高校优势学科建设工程项目

联系人：居后鸿E－mail：luxemberg＠nuaa.edu.cn