永磁交流伺服系统定位末端抖动抑制
2015-01-25杨明龙江唐思宇易晨
杨明, 龙江, 唐思宇, 易晨
(哈尔滨工业大学电气工程系,黑龙江哈尔滨150001)
0 引言
高速和高精度始终是伺服系统至关重要的技术指标。然而,在伺服系统高速定位的末端往往会发生强烈的振动,这会严重影响伺服系统的轨迹跟踪和定位性能。究其原因,是因为伺服系统中往往存在着弹性减速装置。这些减速装置能在低速时提供大的驱动转矩,但同时会引起电机与负载之间的弹性扭转,从而造成伺服系统定位末端振动,因此在设计伺服系统控制器时,必须考虑这些弹性减速机制。通常伺服系统中弹性负载可以用双惯量谐振系统模型来表示[1-6]。
对于伺服系统的定位末端抖动抑制问题人们提出过很多方法,主要分为优化弹性连接装置、主动抑制方式和被动抑制3类方法。其中,“优化弹性连接装置”是通过优化弹性联接装置的设计,以及改进零件加工和装配的工艺,避免机械谐振发生,或者将抖振频率提高到系统工作的带宽之外,减小其对系统造成的影响,不过该方法在实际操作中,受到成本、操作难易程度等很多客观条件的限制,有很大的局限性,还需要配合其他方法来进行抑制。“主动抑制方式”就是主动改变控制器参数或控制其结构用以抑制末端抖动。例如Hwang等提出了利用状态反馈控制来提高硬盘驱动器读磁头的性能,其主要难点在于谐振辨识和状态反馈控制器的设计[7]。Well等在状态观测器基础上在位置末端增加感应器来进行反馈控制[8],但在实际中,另加的感应器使得这项技术难以实现。“被动抑制方式”是指仅仅增加简单的补偿或滤波算法对弹性末端抖动进行抑制,不需要改变系统的控制结构以及控制器参数。常用的方法是加入滤波器对位置命令输入进行处理,根据末端抖振的频率,消去给定命令中的相关频率成分,从而抑制了弹性负载定位末端抖动[9-11]。
本文首先介绍了负载-电机双惯量系统模型,并结合系统零极点分析了定位末端抖动的本质原因,然后使用陷波滤波器的被动抑制方法,较好地抑制了定位末端的抖动现象,但是使用陷波滤波器同时会引起系统的相位滞后。为此,又提出了一种带补偿环节的滤波改进方法,实现了既抑制位置环定位末端抖动,同时减小相位滞后、提高系统带宽,从而更好地提升伺服系统位置环性能。最后通过仿真实验证明了该算法的有效性。
1 伺服系统位置环控制系统
1.1 负载-电机双惯量系统模型
伺服系统中的弹性连接装置可以近似认识是一个双惯量机械传动系统,如图1所示。电机和执行机构通过传动轴系联接,传动轴系具有一定的抗扭刚度K和阻尼系数Cw。当传动轴系发生扭转形变时轴系将产生转矩Tw,此转矩对于电机来说可看作是电机的负载转矩,而对于执行机构来说可看作是驱动转矩。伺服驱动器控制电机运行,为电机的转轴提供电磁转矩Te。在电机端电磁转矩Te和传动轴系转矩Tw作用于转动惯量为J1、阻尼系数为C1的电机转轴。在执行机构端,执行机构具有大小为J2的等效转动惯量以及阻尼系数C2,传动轴系转矩Tw与负载转矩Tl共同作用于执行机构最终决定了负载转速。根据以上分析可建立微分方程组,如式(1)所示。
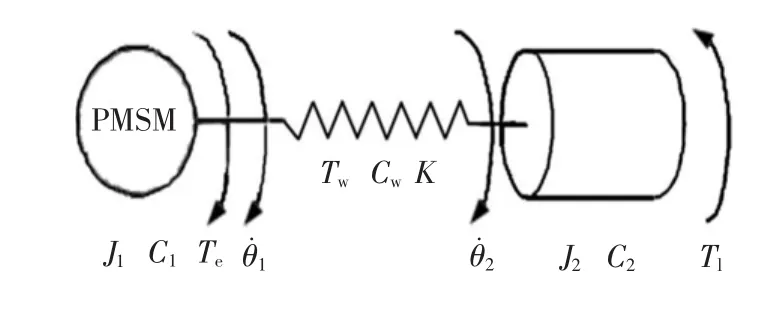
图1 典型双惯量机械传动装置模型Fig.1 Model of typical two-mass transmission mechanisms

根据式(1),并忽略系统中较小的阻尼系数,可推导出电机转速、负载转速以及电机电磁转矩之间的传递函数,分别为
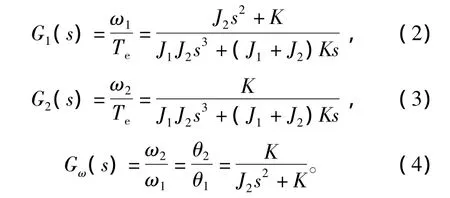
1.2 带弹性连接装置的伺服系统位置环控制系统
图2为实际包含弹性传动装置的伺服系统位置环控制系统框图[12],其中弹性装置的特性在传递函数G1(s)和Gω(s)中体现,这2个环节是弹性双惯量系统与刚性系统的主要区别所在。外环为位置环,位置控制器为Cp(s)。里面为速度环,转速调节器为CV(s),Kτ为转矩常数。通常 Cp(s)=KPP,CV(s)=KVP(1+KVI/s)。结合式(2)和式(4)的机械系统传递函数,即可得出带弹性装置的系统传递函数,如式(5)。
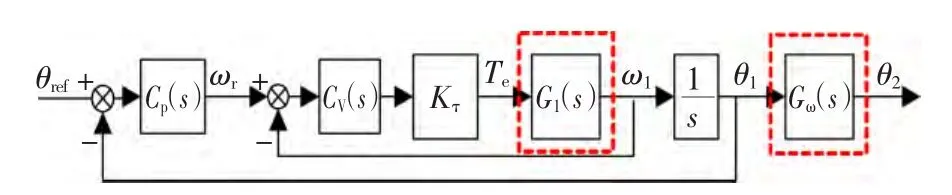
图2 带弹性装置的位置环系统模型框图Fig.2 Block diagram of position loop with elastic transmission mechanisms

2 位置环定位末端抖动抑制
2.1 位置环定位末端抖动分析
为了深入分析定位末端抖动问题,需要画出系统的根轨迹图。在图2所示的位置环控制系统中,Cp(s)和CV(s)分别为选取P控制器和PI控制器,且系统仿真参数如表1所示。
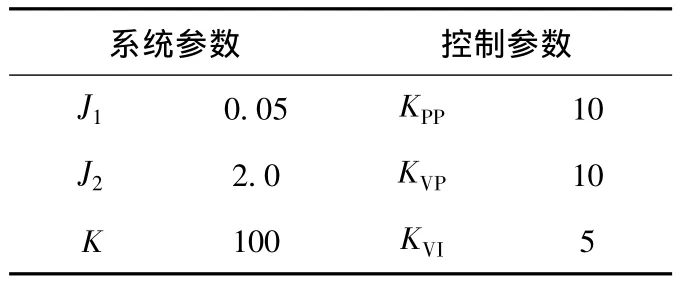
表1 系统参数Table 1 System parameters
根据所给参数,代入式(5)的系统传递函数中,可以得到抑制前伺服系统位置环的根轨迹图,如图3所示。图中A点的极点被零点消去(控制器的作用),B点处极点此时为系统主导极点,其对应的阻尼系数为0.121,为轻阻尼极点,引起系统欠阻尼震荡,从而造成位置末端定位抖动,B极点的频率是5.15 rad/s,即为定位末端抖动的频率。所以,抑制定位末端抖动的实质就是要消去B点处的轻阻尼振动点。
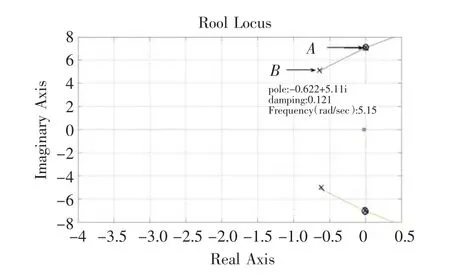
图3 抖振抑制前伺服系统位置环根轨迹图Fig.3 Root locus of servo position loop before suppression
2.2 位置环定位末端抖动的抑制方法
用前向通道陷波滤波器来消除振动极点B,如图4所示,这里陷波滤波器置于位置指令之后,通过消除位置给定指令中的振动频率成分,抑制定位时末端抖动现象。

图4 引入前向通道陷波滤波器后系统结构Fig.4 Structure of system with feed-forward notch filter
陷波滤波器的传递函数如式(6)所示,其中,根据滤波器作用的频率点ω0、陷波带宽参数k1以及陷波深度参数k23个变量可决定滤波器的a、b、c 3个系数。这里陷波滤波器通过系统的伯德图上面取点的方法来配置[13]。
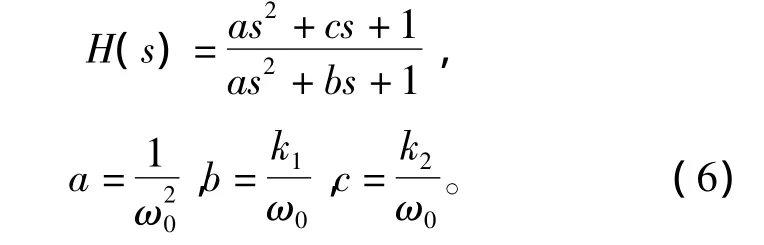
图5为抑制前闭环系统的伯德图,通过伯德图可得到振动频率ω0=5.15 rad/s处的幅频信息,然后取振动频率ω0左右幅值衰减3 dB的两个频率点,可以得到,其中频率较大的点为ωH3dB=5.62 rad/s,频率较低的点为ωL3dB=4.3 rad/s,这样k2由以下公式(7)得到,而陷波宽度参数 k1这里由经验公式(8)得到。配置好的陷波滤波器如公式(9)所示。
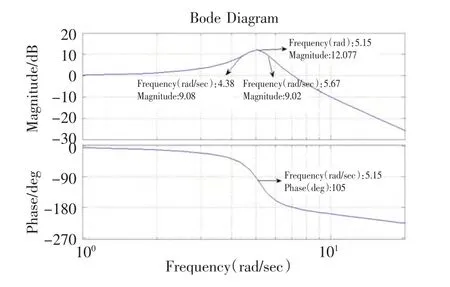
图5 抖振抑制前伺服系统位置环的伯德图Fig.5 Bode diagram of system before suppression
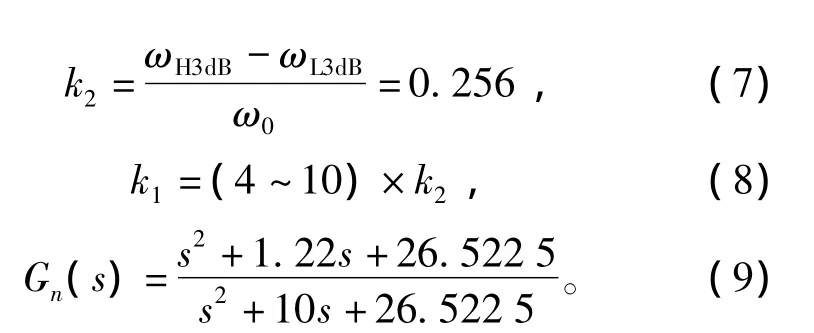
加入陷波滤波器后伺服系统的根轨迹如图6所示,可以看出陷波滤波器的零点与B处极点相互消去,同时引入一个新的极点C,C处极点的阻尼系数为0.947,接近于临界阻尼,从而抑制了定位末端的抖动现象。这时系统的极点位置如表2所示。
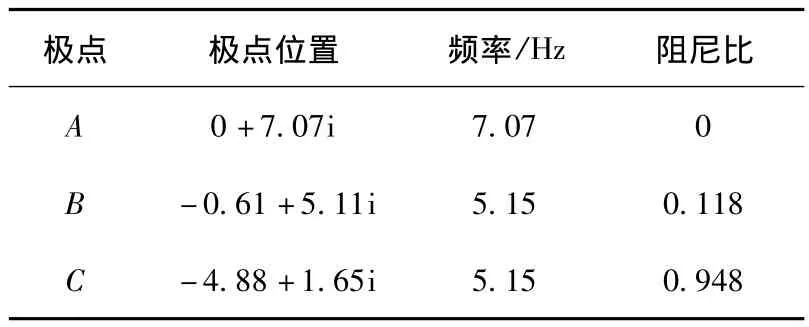
表2 系统极点分布Table 2 Pole location
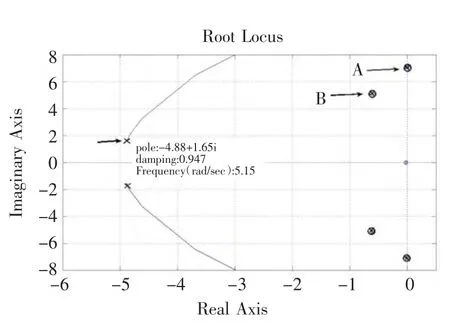
图6 加入陷波滤波器的伺服系统根轨迹图Fig.6 Root locus of system with notch filter
图7 为加入陷波滤波器后系统的伯德图,从伯德图可以看出,这时系统的抖振凸起点已经基本被抑制。但也可以发现系统在抖振点附近会引入一个相位滞后,截止频率变小,带宽变窄。为此,提出一种改进方法。
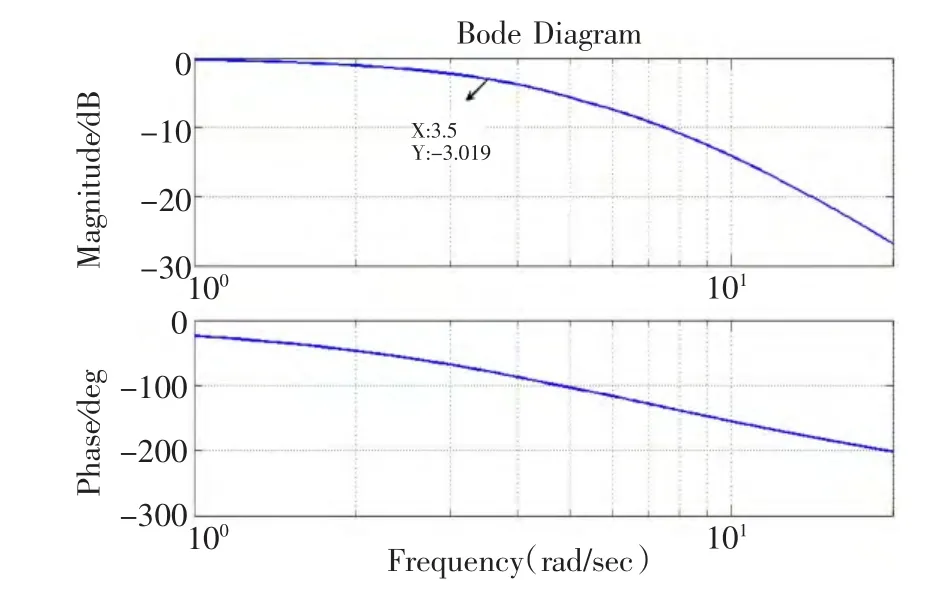
图7 加入陷波滤波器后系统的伯德图Fig.7 Bode diagram of system with notch filter
2.3 定位末端抖动抑制的改进方案
如图8中虚线框内所示,改进方案通过加入一个补偿环节,使得在暂态过程,微分环节通过补偿系数环路起作用,从而解决相位滞后和响应时间的问题;而在位置稳态时,由于微分作用为零,补偿系数也失去作用。补偿环节前后的位置给定应该保证没有静差,所以补偿系数应满足一定条件。

图8 改进方案的结构Fig.8 Structure of improved approach
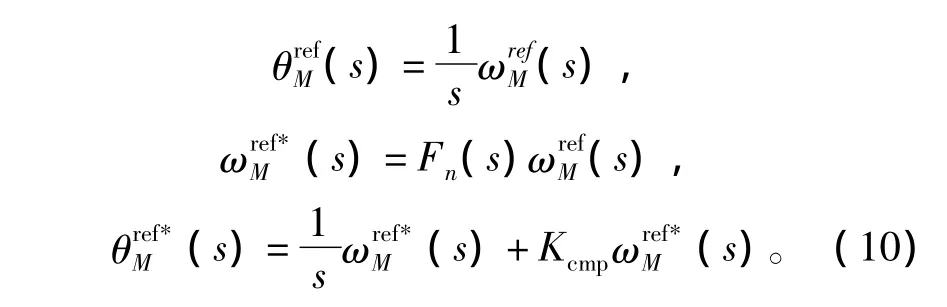
由此可以得到改进滤波前后位置给定误差为
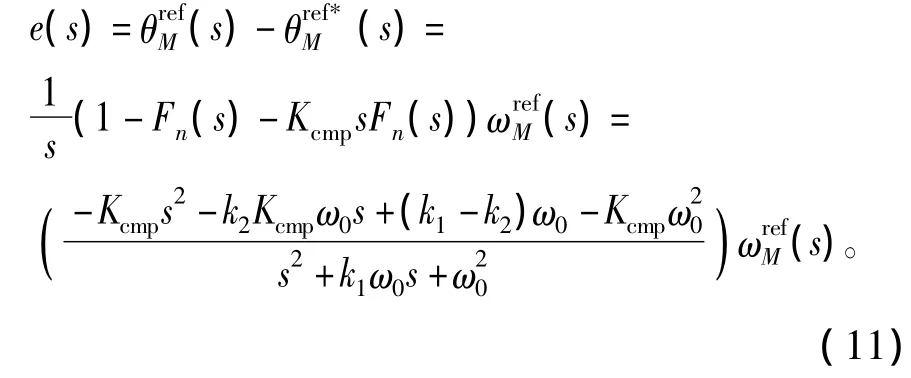
由式(11)可知,位置给定误差和速度给定之间的关系仅仅由陷波滤波器来决定。在稳定状态下,即s=0,位置给定为零的条件为

由上式可以求得,Kcmp应满足

图9为改进前后滤波环节频率响应的对比图,可以看出通过改进方案相当于在高频区加入一个类微分环节,这样响应速度和相位滞后的问题得到了改善。图10为使用改进方案之后系统的伯德图,可以看出通过改进之后的方案系统的带宽明显变宽,即响应速度变快。
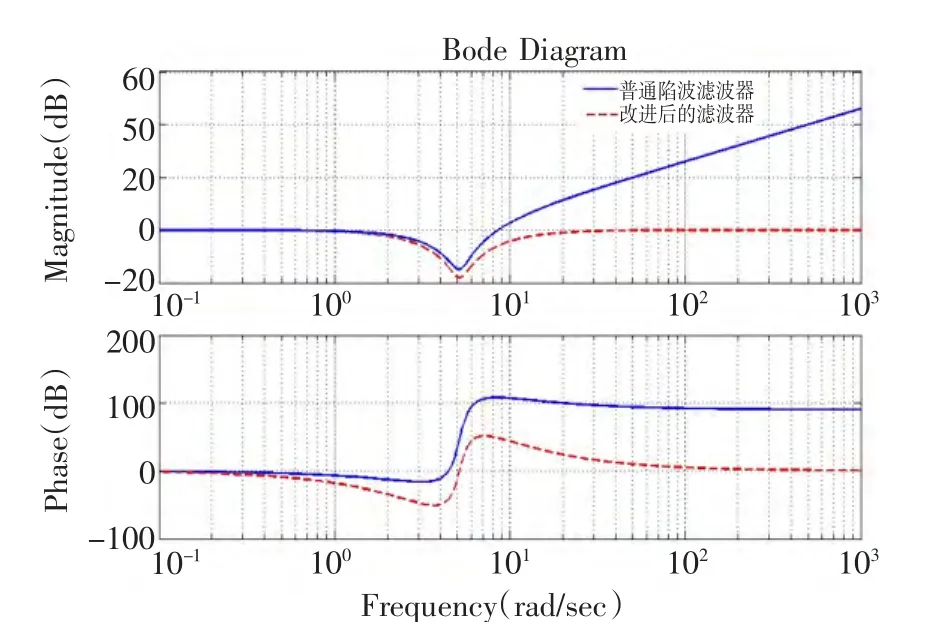
图9 改进前后滤波环节的频率响应对比Fig.9 Comparison of frequency response
图11 为使用未加补偿的陷波滤波器抑制定位末端抖动的仿真波形。可以看出加入陷波滤波器前,系统定位时会有明显的抖动现象,影响伺服系统性能。而加入配置好的陷波滤波器之后,定位末端抖动会有明显的抑制效果,但是同时也发现加入滤波器后响应时间会明显变长。
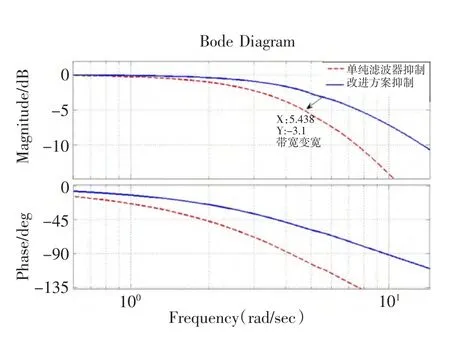
图10 改进方案抑制后系统的伯德图Fig.10 Bode diagram of system adopting improved approach
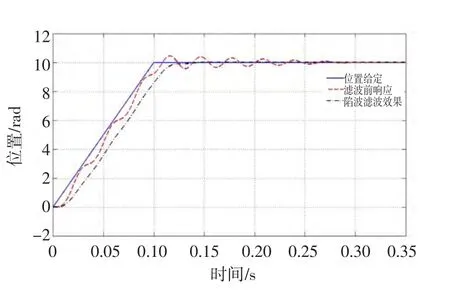
图11 陷波滤波器的抑制效果的仿真结果Fig.11 Simulation result of suppression with notch filter
图12 为改进方案的仿真结果,可以看出相比于改进前滤波器带来的滞后效果,改进后响应时间明显变短,实现了既消除了末端抖动,又缩短了响应时间,很好的验证了之前的分析。

图12 改进方案的仿真结果Fig.12 Simulation result of improved approach
3 实验结果及分析
在DSP(TMSF2812)为运算单元的自制数字化永磁同步伺服系统平台上进行实验。其中驱动器为实验室自制的HIT-750w伺服驱动器,如图13所示,主要参数见表3。

图13 实验驱动器与电机Fig.13 Servo driver and moter
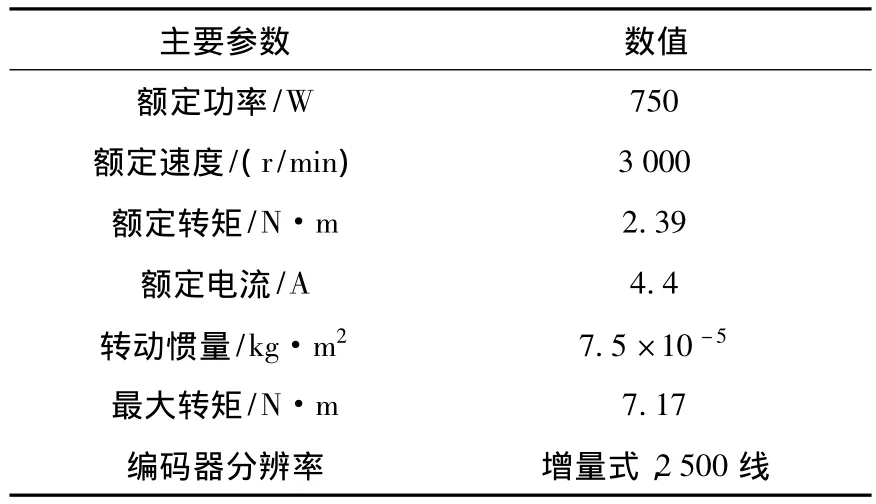
表3 HIT-750w伺服驱动器主要参数Table 3 Main parameters of servo driver HIT-750w
图14为模拟弹性传动装置下的定位末端抖动摆臂平台的实物照片。左右两边伺服电机通过皮带传动带动大惯量摆臂转动,电机与摆臂的传输比为1∶9,摆臂的惯量可以通过在上面的惯量块的位置来调节。通过左右两边摆臂定位效果可以对比不同定位末端抖动抑制方法的效果。

图14 定位末端抖动摆臂平台Fig.14 Positioning swing arm platform
把自制HIT伺服电机装在图14所示的定位末端摆臂平台上,在位置环模式下,225 ms内转过2.25圈后停止,这时摆臂正好从6点钟位置转过1/4圈后,定位于3点钟位置。图15为对定位阶段的速度数据进行频谱分析结果,可以看出抖振频率ω0为6.8 Hz左右。
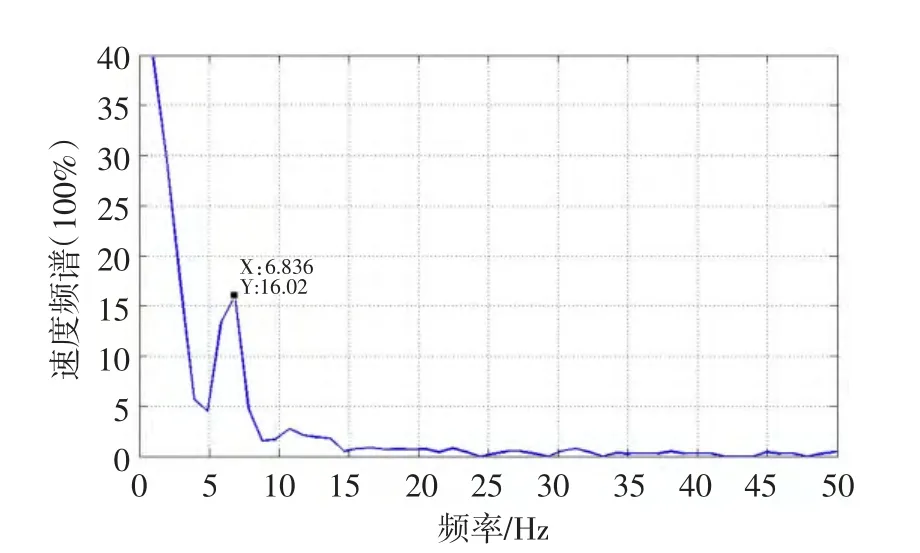
图15 定位抖振频谱分析Fig.15 Spectral analysis of positioning vibration
陷波滤波器参数配置方法如公式(6)所示,其中k1=2,k2=0.2,得到滤波器参数为
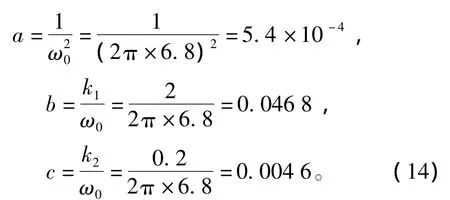
根据补偿系数式(13),可以得到此时补偿系数为Kcmp应设计为0.04。

图16 改进前后的陷波滤波器抑制效果的实验结果Fig.16 Experimental result of improved and unimproved approaches
图16 为改进前后的陷波滤波器抑制定位末端抖动效果的实验结果,其中图16(a)为位置响应,图16(b)为速度响应。可以看出加入陷波滤波器,对定位末端抖动抑制的效果明显,定位时位置响应和速度响应几乎无超调抖振;加入补偿环节后,不仅抑制了伺服系统定位末端抖动,而且相位滞后比单纯用陷波滤波器引起的相位滞后小。实验结果与仿真结果一致,验证了该方法在实际应用中的可行性。
4 结论
对于包含弹性传动装置的伺服驱动系统,本文分析了位置定位末端抖动的机理,并使用陷波滤波器及其改进方案进行抖动抑制,通过仿真及实验对理论方法进行了验证。结果表明,使用陷波滤波器能够消除产生位置末端抖动的低阻尼极点,从而抑制了伺服系统定位末端抖动,但同时也会引入相位滞后,影响系统响应速度。根据所提出改进的滤波方案,不仅实现了定位末端抖动抑制而且加快了位置响应速度。
[1]Ellis G,Lorenz R D.Resonant load control methods for industrial servo drives[J].Industry Applications Conference,2000,3:1438-1445.
[2]Sugiura K,Hori Y.Vibration suppression in 2-and 3-mass system based on the feedback of imperfect derivative of the estimated torsional torque[J].IEEE Transactions on Industrial Electronics,1996,43:56 -64.
[3]Valenzuela M,Bentley J,Lorenz R.Evaluation of torsional oscillations in paper machine sections[J].IEEE Transactions on Industry Applications,2005,41:493 -501.
[4]Jun-Keun J,Seung-Ki S.Kalman filter and LQ based speed controller for torsional vibration suppression in a 2-mass motor drive system[J].IEEE Transactions on Industrial Electronics,1995,42:546-571.
[5]Kiyoshi O.Robust position servo system based on vibration suppression control for industrial robotics[C]//The 2010 International Power Electronics Conference,Japan,2010.
[6]杨明,胡浩,徐殿国.永磁交流伺服系统机械谐振成因及其抑制[J].电机与控制学报,2012,16(1):79-84.YANG Ming,HU Hao,XU Dianguo.Cause and suppression of mechanical resonance in PMSM servo system[J].Electric Machines and Control,2012,16(1):79 -84.
[7]Hwang D,Peng S,Hsu P.An integrated control/diagnostic system for a hard disk drive[J].IEEE Transactions on Control Systems Technology,1994,2:318 -326.
[8]Wells R L,Schueller J K,Tlusty J.Feed-forward and feedback control of a flexible robotic arm[J].IEEE Control Systems Magazine,1990,10:9 -15.
[9]Hisashi K,Toshimasa M,Kiyoshi O.Tracking control for industrial robot using notch filtering system with little phase error[J].E-lectrical Engineering in Japan,2011,175(1):29 -35.
[10]张磊,刘永光,付永领,等.基于自适应陷波器的主动隔振仿真研究[J].系统仿真学报,2005,17(1):234-237.ZHANG Lei,LIU Yongguang,FU Yongling,et al.Study on simulation of AVI based on adapitive notch filter[J].Journal of System Simulation,2005,17(1):234-237.
[11]Hisashi K,Somsawas T,Kiyoshi O.Motion control of industrial robot using new Notch filtering system for vibration suppression and little phase error[C]//Proceedings of International Conference on Mechatronics,Kumamoto,May,2007.
[12]方钦,周顺荣,金如麟.永磁同步电机位置伺服系统的设计[J].微电机,2006,39(2):56 -58.FANG Qin,ZHOU Shunrong,JIN Rulin.Position-servo system design of the PMSM[J].Micromotor,2006,39(2):56 -58.
[13]Hsu W C,Lai C L,Hsu P L.A novel design for vibration suppression for lightly-damped servo control systems[C]//Proceedings of 2011 8thAsian Control Conference,Kaohsiung,Taiwan,May,2011.
