单相PWM整流器死区补偿方法

赵鲁， 李耀华， 葛琼璇， 任晋旗， 马逊

(中国科学院电子研究所电力电子与电气驱动重点实验室，北京100190)

0 引言

在PWM变流器中，为防止同一桥臂两个器件直接导通现象，需根据器件功率等级的不同注入相应的死区时间。死区时间在保证开关器件安全、可靠运行的同时，也带来了十分不利的死区效应，其主要影响会使输出电压基波幅值降低，较低次谐波增加，电流波形发生畸变。针对死区效应这一问题，国内外学者开展了大量的研究工作，并提出多种死区补偿方法。

电流大于零和小于零对输出电压的影响是不同的，需要对电压做不同的补偿［1－2］。如何确定相电流的过零点是死区补偿的关键，文献［3］直接根据检测的电流方向进行电压补偿，由于不可避免地检测电流中的噪声，使得过零点检测难以精确，如果加以滤波又会引起相位延迟，不能及时检测出过零点，因此这种方法补偿效果不理想。文献［4－5］利用硬件电路实时检测功率管的实际导通时间，得到逆变器的实时死区时间，无需电流过零点的检测或预估取得了较好的补偿效果，但是这种方法需要额外的硬件装置，增加了系统的复杂性。文献中对三相电压型PWM逆变器死区补偿方法的研究相对较多，文献［6］基于预测电流控制方法对死区补偿进行了分析，文献［7］利用旋转轴系中的励磁电流和转矩电流分量经过坐标反变换，判断电流在两相静止轴系所处的扇区来决定需要施加的补偿电压。文献［12］提出一种新颖的自适应死区补偿策略，该策略无需电流极性检测，在同步旋转坐标系下，通过PI控制器调节扰动观测器观测出的q轴扰动电压，获得死区补偿时间。

详细地分析了死区效应机理，对单相PWM整流器死区补偿提出了一种新方法。不直接根据检测的电流方向进行电压补偿，而是根据网侧电压通过谐振控制器锁相环的观测值进行判断。当整流器单位功率因数运行时，通过对网侧电压值的观测从而间接地实现了对电流方向的准确判断;当整流器不为单位功率因数运行时，可以根据观测的电压值及相应的功率因数进行电流波形等效计算，同样可以进行相应的死区补偿。通过PSIM电力电子仿真软件进行相应仿真，仿真结果验证了理论分析的正确性;最后在实验样机上进行实验验证。

1 主电路拓扑

图1为单相电压型单个H桥PWM整流器主电路拓扑。其中，us为电网电压;Is为网侧输入电流;Transformer为整流变压器，原边一套绕组、副边两绕组，两个副边绕组分别接入对应H整流桥，两H桥并联运行(这种拓扑应用于列车牵引场合)，只利用其中一个H桥进行相应实验，变压器变比为1∶1;Is1为变压器输出电流;L1为输入滤波电感;Cr、Lr、Rr为两倍频谐振电容、电感、电阻，其作用滤除直流母线电容电压两倍频波动;Cd为支撑电容;udc为直流母线电压;Rload为纯电阻负载;IGBT1、IGBT2、IGBT3、IGBT4为IGBT开关器件。

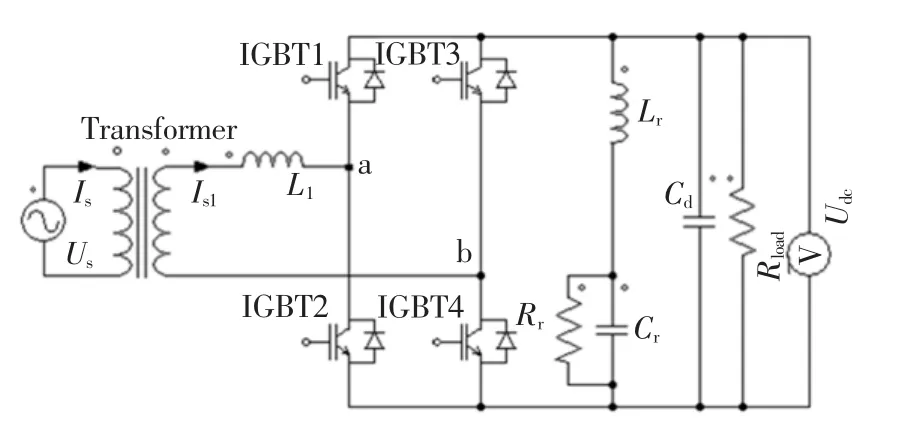
图1 单相PWM整流器主电路拓扑Fig.1 Topology of single-phase PWM rectifier

2 控制策略

图2为单相PWM整流器控制策略框图，以直流母线电压控制环作为外环，对输入电流幅值进行控制;以输入电流的控制作为内环。外环为直流量的控制，采用PI控制器，输出作为电流幅值的给定值。内环为交流量，采用比例+谐振(PR)控制器，可以实现对电流的无差控制。对于电网电压振动项，可以通过电压前馈补偿予以消除。本文采用单相性SPWM调制策略，基于谐振锁相环对电网电压相位信息进行观测，可以实现相位无静差跟踪。电压前馈量与电流内环谐振控制器PR输出量之差为整流器输入电压参考值。当考虑死区补偿时，基于谐振控制器锁相环观测后的电压值进行判断，并引入电压补偿量ΔU，补偿原理将在后面进行介绍。

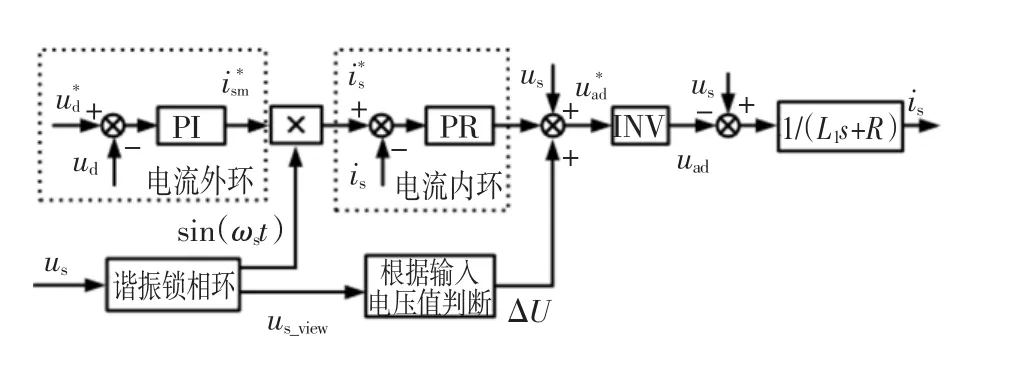
图2 单相PWM整流器控制策略框图Fig.2 Control strategy diagram of single-phase PWM rectifier

因传统的单相锁相环方法存在本身的不足，所以采用谐振控制器锁相环对网侧电压进行观测。谐振控制器锁相环具有良好的相位跟踪效果，可以实现相位无差跟踪，其原理框图如图3所示。

图3 谐振控制器锁相环原理框图Fig.3 Structure of resonant controller phase-locked loop

谐振控制器锁相环是基于谐振控制器构成带通滤波器对网侧电压相位进行观测，图3中y对于v的传递函数为

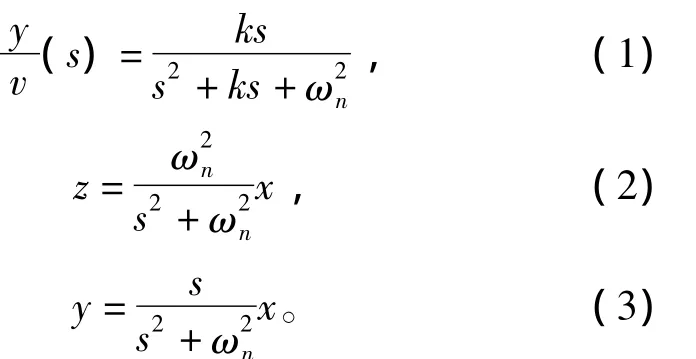
显然这是一个带通滤波器，且无论k取何值，只要k＞0，该滤波器总是稳定的。y可以无差地跟踪v中角频率为ωn的正弦信号，z滞后y的角度为90°，且z与y的幅值相等。这种结构的带通滤波器既可以从v中的滤波得到角频率为ωn的信号，还可以得到滞后其90°的量，其中k用来调节带通滤波器的带宽。根据z与y的瞬时值，可以得到如下表达式，

式中，θ为v中角频率为ωn的正弦信号瞬时角度，vm为v中角频率为ωn的正弦信号幅值。

图4(a)为谐振控制器锁相环的频率特性图(k=0.3)，图4(b)为谐振控制器锁相环的阶跃响应特性图(k=0.3)。从上图中可以看出，对频率为50Hz的信号具有无穷大增益;5～6个周期(0.1～0.12 s)后，相位与幅值跟踪达到稳态值，偏差近似为零。图4(c)为谐振控制器锁相环的仿真波形，输入信号v含有丰富的谐波，输出信号y为观测值，经过5～6个周期(0.1～0.12 s)后，相位与幅值跟踪无偏差，与图4(b)阶跃响应结果一致。上面的理论分析及仿真结果表明，谐振控制器锁相环鲁棒性好，可以实现幅值、相位无差跟踪，而且数字离散化比较简单，计算时间比较短，对CPU要求不高。

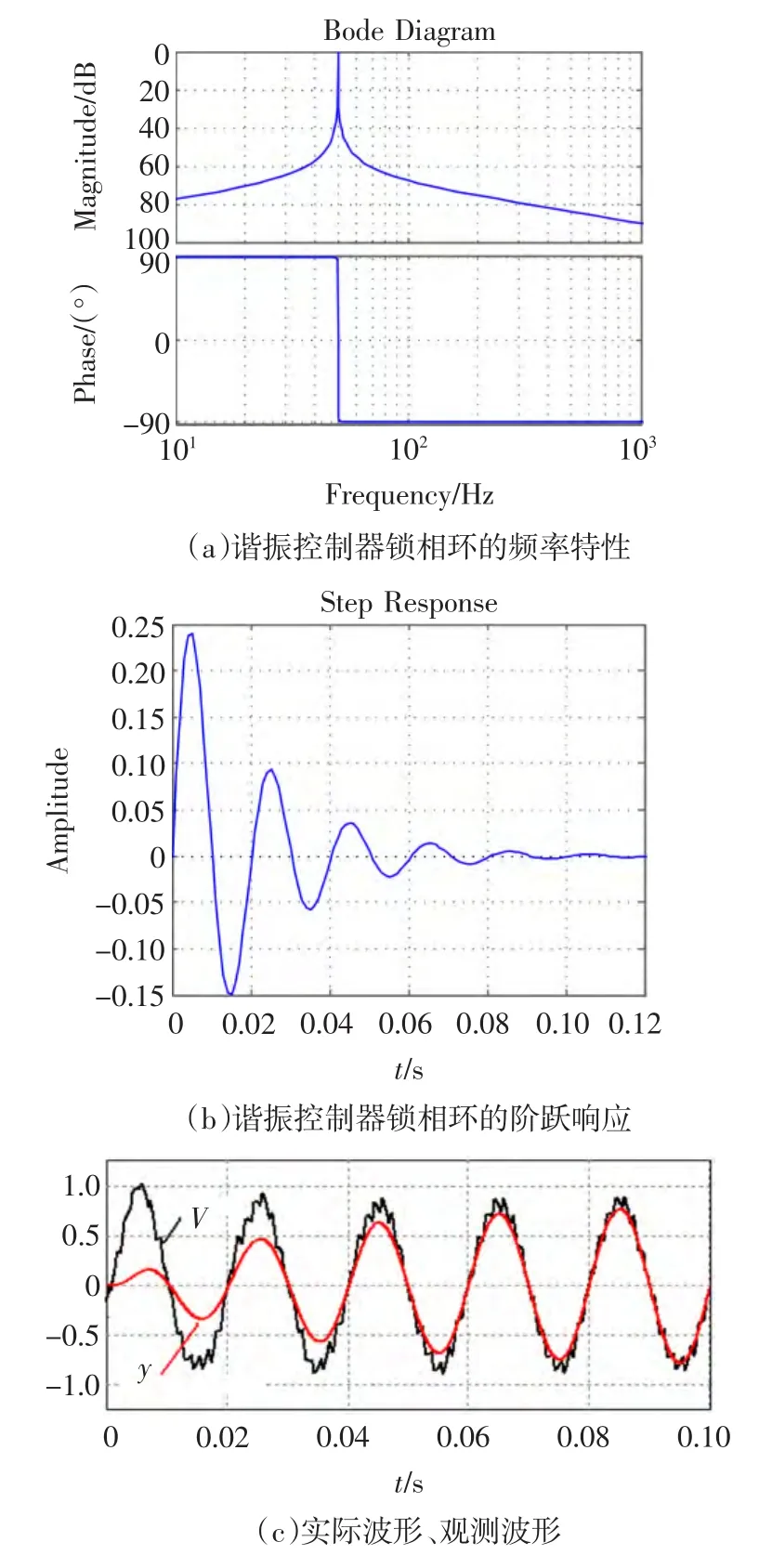
图4 谐振控制器锁相环特性分析Fig.4 Performance analysis of resonant controller phase-locked loop

3 死区补偿原理分析

图5为Is＜0时死区补偿原理框图，图5(a)为没有死区补偿时器件导通、关断状态及电压输出波形。IGBT1、IGBT2、IGBT3、IGBT4为器件理想导通、关断状态;IGBT1'、IGBT2'、IGBT3'、IGBT4'为器件考虑死区效应时导通、关断状态;uab为理想状态整流器输入电压波形，u'ab为考虑死区效应时整流器输入电压波形，Δu为考虑死区效应整流器输入电压产生的偏差量。图5(b)为引入死区补偿时器件导通、关断状态及电压输出波形。补偿原理是在每个开关周期内，将第一个桥臂IGBT1提前导通、IGBT2提前关断，第二个桥臂IGBT3提前关断、IGBT4提前导通，提前的时间为设置的死区时间，电压偏差量ΔU为零。因采用单相性SPWM调制策略，所以每个桥臂参考电压对应的方程表达式如下所示。

第一个桥臂为

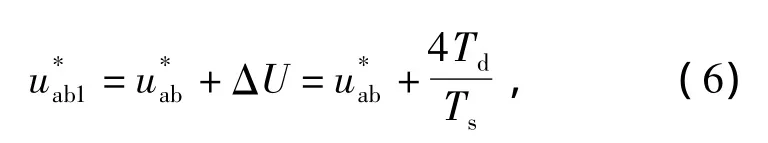
第二个桥臂为

式中，Td为死区时间，Ts为三角载波周期值为整流器输入电压参考值为死区补偿后电压参考值。

图5 Is＜0时死区补偿原理框图Fig.5 Dead time compensation block diagram when Is＜0

图6 为Is＞0时死区补偿原理框图，图6(a)为没有死区补偿时器件导通、关断状态及电压输出波形;图6(b)为引入死区补偿时器件导通、关断状态及电压输出波形。补偿原理是在每个开关周期内，将第一个桥臂IGBT1提前关断、IGBT2提前导通，第二个桥臂IGBT3提前导通、IGBT4提前关断，提前时间为死区时间，电压偏差量ΔU为零。因本文采用单相性SPWM调制策略，所以每个桥臂参考电压对应的方程表达式如下所示。

第一个桥臂为

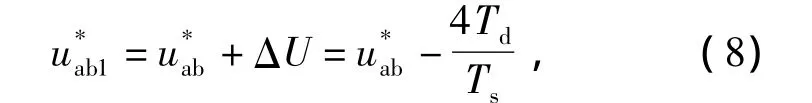
第二个桥臂为

死区补偿是基于Is的值进行判断，分成大于零、小于零两种情况。然而电流波形并非标准正弦波形，在零点附件很容易产生零点箝位现象。为了避免这种现象，提出采用网侧输入电压us基于谐振锁相环的观测值us－view进行判断，因为观测值us－view只存在基波分量，是一个标准的正弦量。整流器单位功率因数运行，网侧输入电压us与电流Is同相位，采用网侧电压观测值us－view取代输入电流瞬时值，即可以准确补偿死区又避免了电流的谐波干扰。当us－view＜0 时，采用式(6)、(7)进行死区补偿，当us－view≥0 时，采用式(8)、(9)进行死区补偿。

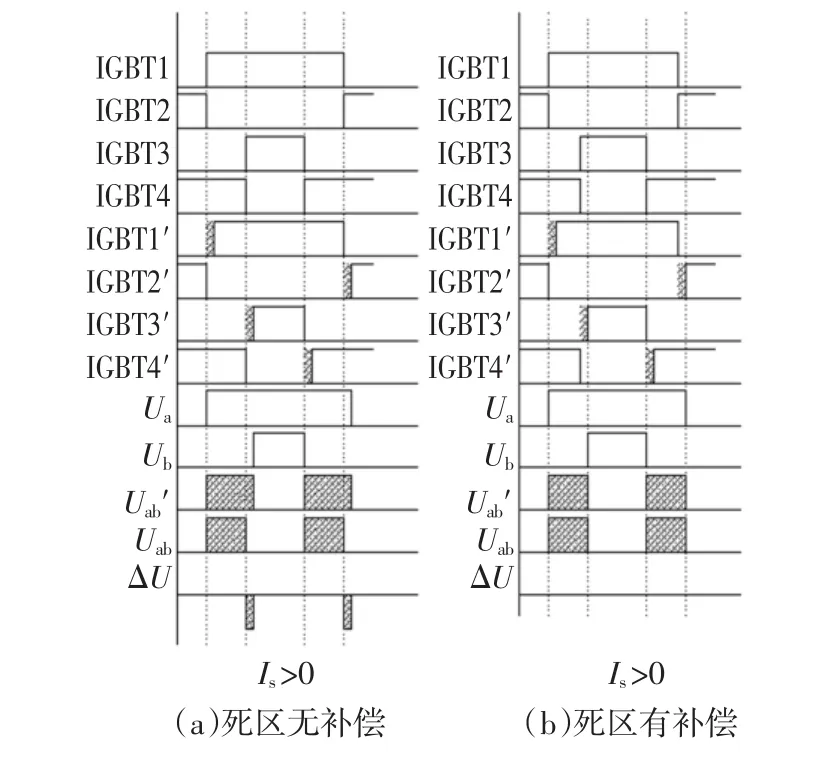
图6 Is＞0时死区补偿原理框图Fig.6 Dead time compensation block diagram when Is＞0

4 仿真分析

为了研究单相PWM整流器死区补偿策略的正确性，采用电力电子专用仿真软件PSIM，对单相电压型PWM整流器进行仿真。

表1 单相PWM整流器参数Table 1 Parameters of single-phase PWM rectifier

1)负载运行

以电网频率50 Hz、开关频率4 kHz、网侧输入电压有效值us=396 V，负载电阻Rload=23.4 Ω，死区时间td=5 μs为例进行仿真分析，其中主电路如图1所示，PWM整流器参数如表1所示，控制策略如图2所示。图7为没有加入死区补偿的仿真结果，图7(a)为输入电流Is的仿真波形图，图7(b)为电流Is的各次谐波含量分布图，总谐波畸变率为9.1%。图8为基于电流值进行直接判断，加入死区补偿的仿真结果，图8(a)为输入电流Is的仿真波形，图8(b)为电流Is的各次谐波含量分布图，总谐波畸变率为7.63%。图9为基于电压观测值进行判断，加入死区补偿的仿真结果，图9(a)为基于电压us的观测值进行判断时，输入电流Is的仿真波形，图9(b)为电流Is的各次谐波含量分布图，总谐波畸变率为6.0%。基于电压观测值进行死区补偿，输入电流总谐波畸变率大大下降，电流零点箝位现象不再明显，从而证明了死区补偿新方法的有效性。

图7 无死区补偿仿真波形Fig.7 Simulation waveforms of no dead time compensation

图8 有死区补偿仿真结果—基于电流值判断Fig.8 Simulation waveforms of dead time compensation judged by current

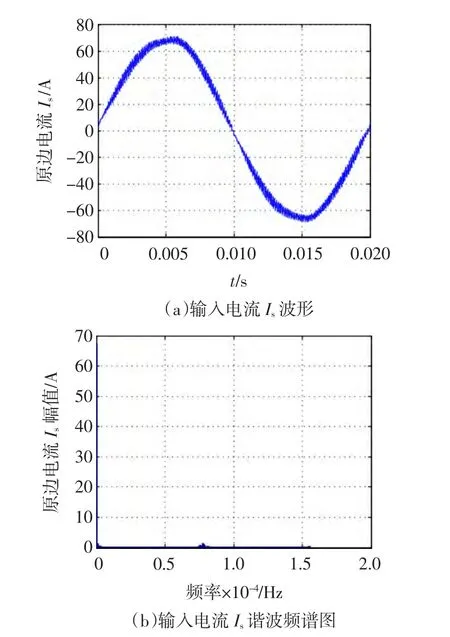
图9 有死区补偿仿真结果—基于电压观测值判断Fig.9 Simulation waveforms of dead time compensation judged by voltage

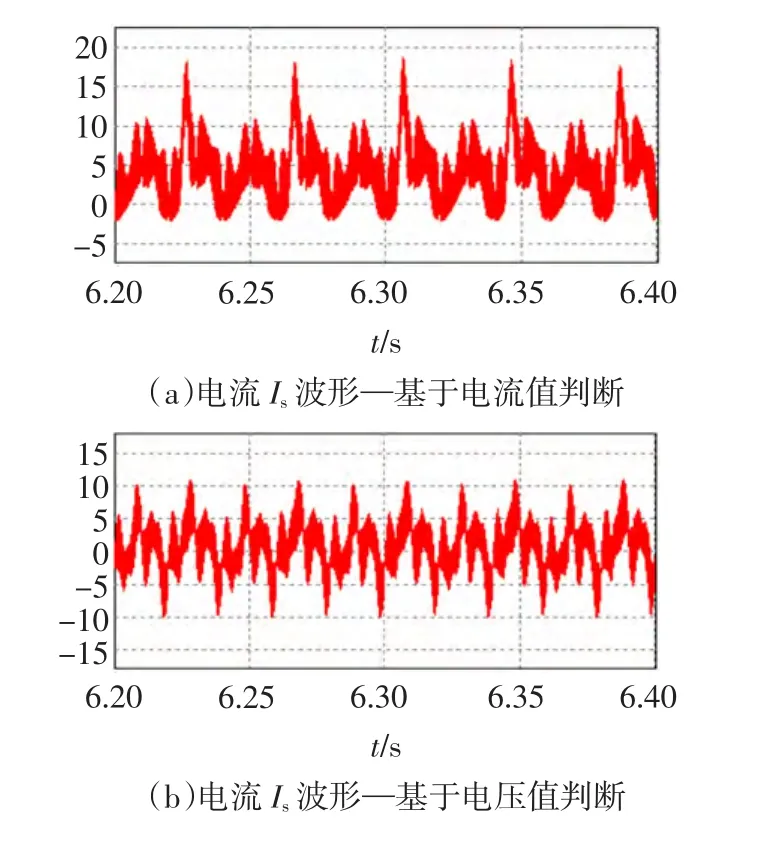
图10 整流器空载仿真电流波形Fig.10 Simulation waveforms of rectifier current on no-load

2)空载运行

为了进一步对比分析整流器轻载时采用电流瞬时值、网侧电压观测值进行死区补偿效果，图10给出了整流器空载运行时输入电流波形，将负载电阻Rload移除。从上面仿真波形中可以看出，基于网侧电压观测值进行死区补偿的效果要比瞬时电流值补偿好。

3)电网电压畸变

为了分析电网电压发生畸变或频率产生抖动时对整流器死区补偿的影响，假设电网电压表达式如式(10)所示，除基波外还包含250、550、1 550 Hz分量，对应的有效值分别为5、10、15 V。

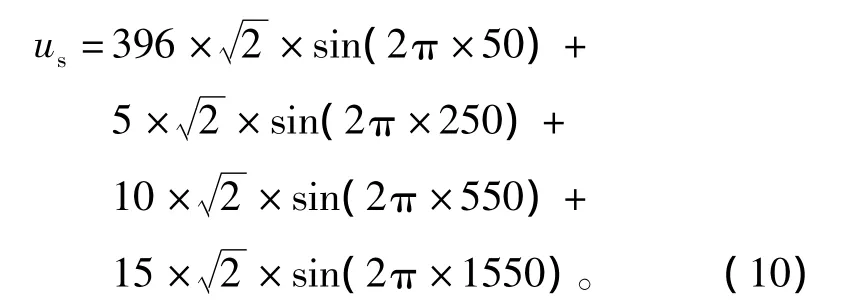
图11为电网电压畸变时的仿真结果，控制器参数与上面负载运行时一致。图11(a)为网侧输入电压us及其观测值us－view仿真波形，谐振锁相环可以实现电网电压相位无静差跟踪。图11(b)为网侧输入电压、电流波形，实现单位功率因数运行。图11(c)、图11(d)、图11(e)分别为无死区补偿、基于电流值死区补偿、基于电压观测值死区补偿电流波形及谐波含量，对应的电流总谐波畸变率分别为10.24%、8.11%、6.43%。与上面电压没有畸变时结果相同，采用基于电压观测值进行死区补偿要比基于电流值效果更好。

图11 电网电压畸变仿真波形Fig.11 Simulation waveforms of voltage distortion

5 实验验证

为了验证单相PWM整流器死区补偿的可行性及仿真结果的正确性，在样机上进行了相应的实验。整流器以TMS320LF28335 DSP为控制核心，开关器件采用1 200 V/150 A的IGBT。输入电流由FLUKE80i－110s电流钳测量，输入电压与直流母线电压由Tektronix P5200差分探头测量得到。实验中的相应参数与上节仿真分析中相同，主电路如图1所示，控制策略如图2所示，主要参数如表1所示，网侧输入电压us=396 V，负载电阻Rload=23.4 Ω，死区时间 td=5 μs。

图12为无死区补偿的实验结果。图12(a)为网侧输入电压us，输入电流Is，整流器输入电压uab，变压器副边绕组输出电流Is1波形，图12(b)为电流Is的各次谐波含量分布图，总谐波畸变率为9.7%。图13为基于电流Is的值进行判断时，死区补偿的实验结果。图13(a)为网侧输入电压us，输入电流Is，整流器输入电压uab，输入电流is1波形，图13(b)为电流Is的各次谐波含量分布图，总谐波畸变率为7.6%。图14为基于电压us的观测值进行判断时，死区补偿的实验结果。图14(a)为网侧输入电压us，输入电流Is，整流器输入电压uab，变压器副边绕组输出电流is1波形，图14(b)为电流Is的各次谐波含量分布图，总谐波畸变率为6.3%。从图中可以看出，采用电压us观测值进行判断时，死区补偿的效果更好。实验结果与仿真结果相同，也说明死区补偿新方法的有效性。

图12 无死区补偿实验波形Fig.12 Experimental waveforms of no dead time compensation

为了验证整流器轻载时采用电流瞬时值、网侧电压观测值死区补偿效果，图15给出了整流器空载运行时输入电流波形。从上面仿真波形中可以看出，基于网侧电压观测值进行死区补偿的效果要比瞬时电流值补偿好。

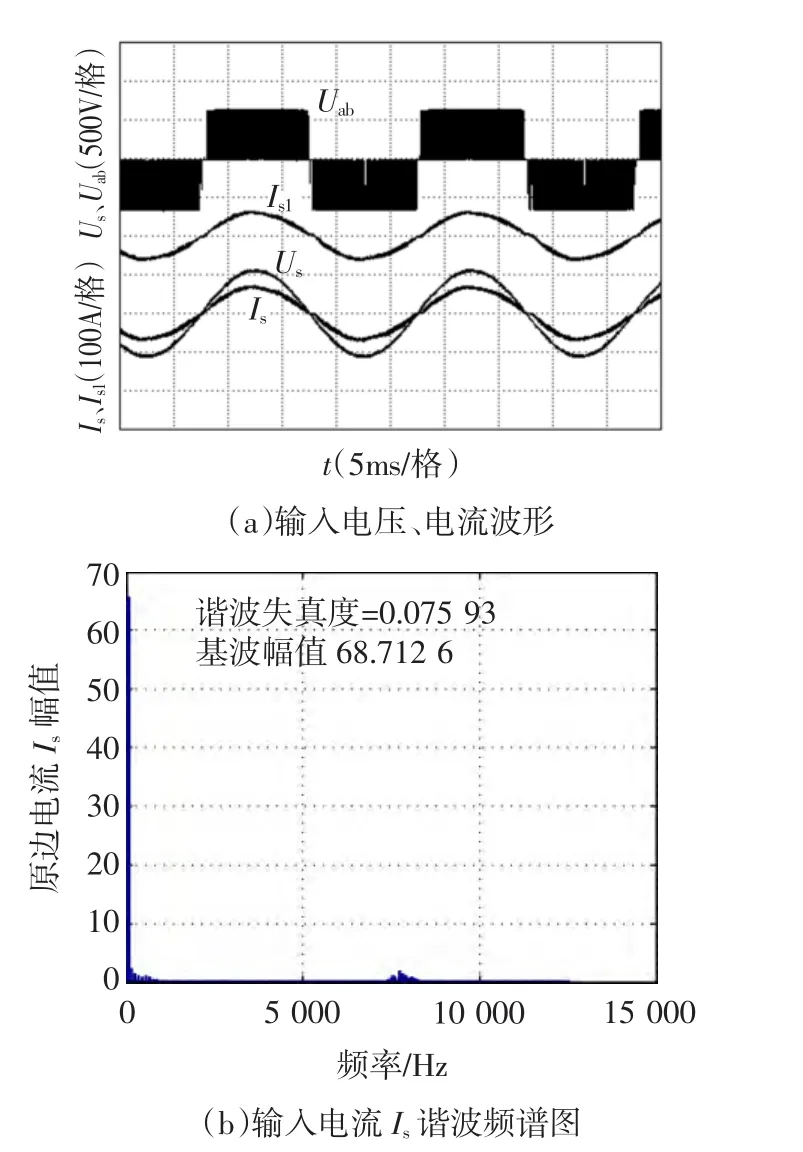
图13 有死区补偿实验波形—基于电流值判断Fig.13 Experimental waveforms of dead time compensation judged by current

图14 有死区补偿实验波形—基于电压值判断Fig.14 Experimental waveforms of dead time compensation judged by voltage

图15 整流器空载实验电流波形Fig.15 Experimental waveforms of rectifier current on no-load

6 结论

本章提出了一种基于网侧电压谐振控制器锁相环的观测值进行判断，对单相PWM整流器死区时间进行补偿的新方法，并与通过电流大小进行直接补偿方法进行对比分析。首先，介绍了单相整流器控制策略，采用电压外环PI及电流内环PR控制器;接着对单相PWM整流器死区效应的原理进行了详细的阐述;最终通过仿真及实验对这种新的死区补偿方法进行验证，采用电压观测值取代电流进行死区补偿效果将更明显。

［1］Naomitsu Urasaki，Tomonobu Senjyu，Katsumi Uezato，et al.Online dead-time compensation method for voltage source inverter fed motor drives［C］//Applied Power Electronics Conference and Exposition，19th Annual IEEE，2004，1:122 －127.

［2］KIM Hyun Soo，KIM Kyeong Hwa，YOUN Myung Joong.On-line dead-time compensation method based on time delay control［J］.IEEE Transactions on Control Systems Technology，2003，11(2):279－285.

［3］窦汝振，刘钧，温旭辉.SVPWM控制逆变器死区补偿方法的研究［J］.电力电子技术，2004，38(6):59－61.DOU Ruzhen，LIU Jun，WEN Xuhui.Research on dead-time compensation of the inverter using SVPWM［J］.Power Electronics，2004，38(6):59 －61.

［4］刘军锋，李叶松.死区对电压型逆变器输出误差的影响及其补偿［J］.电工技术学报，2007，22(5):117 －122.LIU Junfeng，LI Yesong.Dead-time influence on output error of voltage source inverter and compensation［J］.Transactions of China Electrotechnical Society，2007，22(5):117 －122.

［5］YONG-KAI L，YEN-SHIN L.Dead-time elimination of PWM-controlled inverter/converter without separate power sources for current polarity detection circuit［J］.IEEE Transactions on Industrial E-lectronics，2009，56(6):2121 －2127.

［6］刘亮，邓名高，欧阳红林，等.基于预测电流控制的PWM逆变器死区补偿方法研究［J］.电工技术学报，2005，20(8):78－83.LIU Liang，DENG Minggao，OUYANG Honglin，et al.A method to compensate the dead time of PWM inverter based on predictive current control［J］.Transactions of China Electrotechnical Society，2005，20(8):78 －83.

［7］王高林，于泳，杨荣峰，等.感应电机空间矢量PWM控制逆变器死区效应补偿［J］.中国电机工程学报，2008，28(15):79－83.WANG Gaolin，YU Yong，YANG Rongfeng，et al.Dead-time compensation of space vector PWM inverter for induction motor［J］.Proceedings of the CSEE，2008，28(15):79 －83.

［8］吴茂刚，赵荣祥，汤新舟.正弦和空间矢量PWM逆变器死区效应分析与补偿［J］.中国电机工程学报，2006，26(12):101－105.WU Maogang，ZHAO Rongxiang TANG Xinzhou.Dead-time effect analysis and compensation of SPWM and SVPWM inverter［J］.Proceedings of the CSEE，2006，26(12):101 －105.

［9］何正义，季学武，瞿文龙.一种新颖的基于死区时间在线调整的SVPWM 补偿算法［J］.电工技术学报，2009，24(6):42－47.HE Zhengyi，JI Xuexu，QU Wenlong.A novel SVPWM compensation strategy based on regulating dead time online［J］.Transactions of China Electrotechnical Society，2009，24(6):42 －47.

［10］杨立永，陈智刚，陈为奇，等.逆变器输出电压模型及新型死区补偿方法［J］.电工技术学报，2012，27(1):182 －187.YANG Liyong，CHEN Zhigang，CHEN Weiqi，et al.Output voltage medel of VSI-inverter and a novel dead time compensation method［J］.Transactions of China Electrotechnical Society，2012，27(1):182－187.

［11］杨荣峰，陈伟，于泳，等.自适应滤波在电流矢量死区补偿方法中的应用［J］.电工技术学报，2009，24(7):65 －69.YANG Rongfeng，CHEN Wei，YU Yong，et al.Adaptive filter application in current vector dead time compensation ［J］.Transactions of China Electrotechnical Society，2009，24(7):65 －69.

［12］周华伟，温旭辉，赵峰，等.一种新颖的电压源逆变器自适应死区补偿策略［J］.中国电机工程学报，2011，31(24):26－32.ZHOU Huawei，WEN Xuhui，ZHAO Feng，et al.A novel adaptive dead-time compensation strategy for VSI［J］.Proceedings of the CSEE，2011，31(24):26 －32.

［13］SEON-HWAN H，JANG-MOK K.Dead time compensation method for voltage-fed PWM inverter［J］.IEEE Transactions on Energy Conversion，2010，25(1):1 －10.

［14］王少杰，罗安.谐波域死区效应分析及补偿方法的研究［J］.电工技术学报，2009，24(8):111 －119.WANG Shaojie，LUO An.Study of dead-time effect and its compensation stragtegies［J］.Transactions of China Electrotechnical Society，2009，24(8):111 －119.

［15］刘栋良，武瑞斌，张遥，等.基于模糊控制零电流钳位逆变器死区补偿［J］.电工技术学报，2011，26(8):119 －124.LIU Dongliang，WU Ruibing，ZHANG Yao，et al.Inverter dead time compensation of zero current clamping based on fuzzy control［J］.Transactions of China Electrotechnical Society，2011，26(8):119－124.

［16］刘陵顺，尚安利，顾文锦.SPWM逆变器死区效应的研究［J］.电机与控制学报，2001，5(4):237 －241.LIU Lingshun，SHANG Anli，GU Wenjin.Analysis and simulation of the dead-time effect in the PWM converter［J］.Electric Machines and Control，2001，5(4):237 －241.

［17］贾红云，程明，花为，等.基于死区补偿的磁通切换永磁电机定子磁场定向控制［J］.电工技术学报，2010，25(11):48－55.JIA Hongyun，CHENG Ming，HUA Wei，et al.Stator flux oriented control for flux switching permanent magnet motor based on dead time compensation［J］.Transactions of China Electrotechnical Society，2010，25(11):48 －55.