一种永磁同步电机电流直接反馈矢量控制

朱军， 程志磊， 汪旭东， 许孝卓， 封海潮

(河南理工大学电气工程与自动化学院，河南焦作454000)

0 引言

永磁同步电机具有结构简单、效率高、功率因数高、功率密度高、体积小、转矩电流比高、转动惯量低、易于散热和维护保养等特点，被广泛应用到工农业生产、交通、航空航天、国防和日常生活等领域。尤其是随着电力电子技术、微电子技术、微型计算机技术、传感器技术、稀土永磁材料及电机控制理论的发展，永磁同步电机控制系统的研究和推广应用受到了人们的普遍重视［1－3］。

20世纪70年代，西徳学者F.Blashke等提出的感应电机矢量变换技术(Transvector Control)，开辟了现代交流电机调速控制的新纪元，使得交流电机调速系统在调速范围、调速精确度、动态响应等方面发生了质的飞跃，其性能已经超过直流电机调速系统，真正实现了交流电机速度调整的连续、平滑、高效。目前，永磁同步电机的应用已不再局限于恒定频率、恒定转速的场合，由永磁同步电机构成的交流调速系统已在中小容量调速、伺服场合得到广泛的应用。其中，永磁同步电机矢量控制系统能够实现高精确度、高动态性能、大范围的调速或定位控制。随着机器人、数控机床等技术的发展，对高性能变速伺服驱动系统的需求正在不断增长。因此，永磁同步电机矢量控制系统具有广阔的发展和应用前景，对永磁同步电机矢量控制系统的研究已经成为中小型交流调速和伺服驱动系统的研究重点。

文献［4］利用多项式核支持向量机离线训练三角函数，获得矢量控制所需三角函数运算，解决微控制器旋转坐标变换中三角函数运算量大的问题;文献［5］提出一种面装式永磁同步电机电流矢量直接控制技术，类似于经典矢量控制和直接转矩控制的结合体，无需通过旋转坐标变换，直接采用Bang－Bang控制器通过选取合适的空间电压矢量对定子电流矢量幅值和相位进行滞环调节，进而获得优异的转矩动态响应;文献［6］采用含有两个设置频点的多层低通无源滤波器模式改善经典矢量控制对面贴式永磁同步电机控制性能，有效的减小了转矩波动和电流谐波噪声;文献［7］通过在d、q轴电压控制方程式中引入交叉耦合项的方法，使经典矢量控制方法得到改进，从而获得宽速精准的控制性能。由上述学者的研究可知，利用不同的改进方法均可提高经典矢量控制的性能。本文立足于消去Clarke旋转坐标变换而减小矢量控制的运算量及复杂性，引入电流直接反馈的方式对经典矢量控制系统进行改进，以永磁同步电机为载体对改进方法进行实验仿真和定量分析对比研究。

1 PMSM矢量控制及转子磁场定向控制

三相永磁同步电机是一个多变量、强耦合和非线性的复杂系统，要想对它进行直接控制是十分困难的。因此借助于坐标变换［8］，通过解耦使各物理量从静止坐标系转换到同步旋转坐标系。此时，同步坐标系中的各空间向量则变成直流量，把定子电流中的励磁分量和转矩分量变成各自独立标量，从而可以对这些给定量实时控制达到直流电机的控制性能［9］。

1.1 矢量控制

若在实施永磁同步电机控制时，能够独立控制电机定子电流幅值与相位，保证同步电机定子三相电流所形成的正弦波磁动势与永磁体基波励磁磁场保持正交，此时的控制方式即为磁场定向的矢量控制，转子参考坐标系中d、q轴解耦，实现了交流永磁同步电机对直流电动机的严格模拟。若使β=90°，电机每安培定子电流产生的转矩最大，输出转矩和电机电枢电流成正比，可以获得最高的转矩电流比，电动机的铜耗最小。此时，永磁同步电机电枢电流中只有交轴分量，即is=iq。

在实际控制过程中，设法使电机电流的直轴分量、交轴分量与设定值相等，即id=i*d，iq=i*q，即可实现对两个电流分量的单独控制，从而实现矢量控制。设定的交、直轴电流经过Park逆变换成三相电流给定，通过快速电流控制环，使电机实际电流等于给定电流，自然保证id=i*d，iq=i*q。因此，永磁同步电机矢量控制是通过控制d、q轴电流，经过矢量变换或坐标变换而实现的。对id和iq各自独立地控制，可以对电机转矩和气隙磁通独立控制，而转矩和交轴电流具有线性关系，作为控制对象，从外面看进去，此时的PMSM已经等效为他励直流电动机。

1.2 转子磁场定向控制

三相同步电动机的运行原理是依靠定、转子双边励磁，由两个励磁磁场相互作用产生励磁转矩，转矩控制的核心是对定子电流矢量幅值和相对转子磁链矢量相位的控制。由于机电能量转换在定子中完成，因此转矩控制可以直接在定子侧实现。

永磁同步电机在dq轴系的转矩矢量方程式为

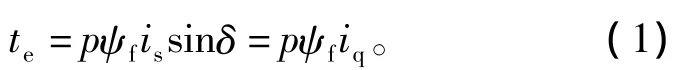
式中:p为电机极对数;ψf为转子(永磁体)磁通，为一常数;is为电机电枢电流，iq为电枢电流的交轴分量，在矢量控制情况下，is=iq;δ为is与d轴夹角。

式(1)表明，通过控制is的幅值和相位，即在dq轴系内控制is的两个电流分量iq和id就可以控制电磁转矩。更进一步可知，决定电磁转矩的是定子电流q轴分量，iq称为转矩电流。但是，这个dq轴系的d轴一定要与ψf方向一致，或者说dq轴系是沿转子磁场定向的，通常称之为磁场定向。

若控制δ=90°电角度(id=0)，则is与ψf正交，is=iq，定子电流全部为转矩电流。虽然转子以电角度wr旋转，但是在dq轴系内is与ψf却始终相对静止，从转矩生成的角度，可将面装式PMSM等效为他励直流电动机。

如前所述，通过控制交轴电流可以直接控制电磁转矩，且te与iq间具有线性关系，就转矩控制而言，可以获得与实际他励直流电动机同样的控制品质。

2 PMSM控制系统建模与仿真

永磁同步电机的参数设置如表1所示。

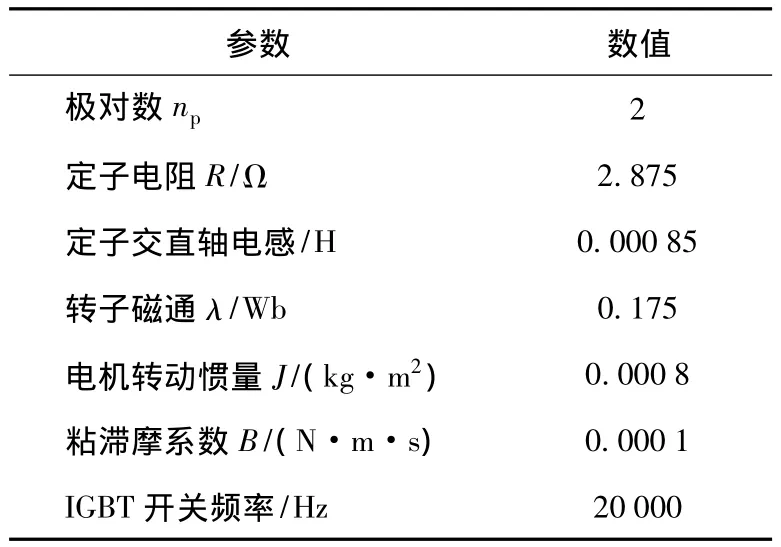
表1 永磁同步电机参数设置Table 1 Parameter setting of PMSM

针对负载变动和转速变化，本文分两种情形进行仿真，假设系统图中的θr通过光电编码器测量获取，从而获得d轴的位置:

情形一:给定电机1 400 r/s，电机带3 N·m负载启动，在0.03 s负载增加为6 N·m，在0.07 s转速减到800 r/s。

情形二:给定电机300 r/s，电机空载启动，在0.03 s负载增加为5 N·m，在0.07 s转速增至1 000 r/s。

2.1 经典矢量控制系统(M1)建模与仿真

基于Matlab/SIMULINK搭建矢量控制系统，系统框图如图1所示。图中速度调节器、转矩调节器均采用PI控制，逆变器PWM采用三角波载波。

情形一时系统的仿真输出如图2所示。

由图2可知，情形一时电机带载高速启动，在0.013 s输出转矩达到稳定，转速在0.008 s即可达到稳定，稳态时转矩和转速纹波较小;在0.03 s负载增加，经0.008 s转矩稳定，但稳态时存在一定的纹波，这一过程中转速几乎不变，保持稳定无纹波;在0.07 s给定转速降低，转矩经0.008 s达到稳态，因为转速适中，转矩在稳态时纹波减小，转速经0.005 s达到稳态，超调很小;全程稳态时电机定子三相电流近似为正弦波形，转换为dq轴系后id近似为0，iq稳定，但存在一定的纹波。

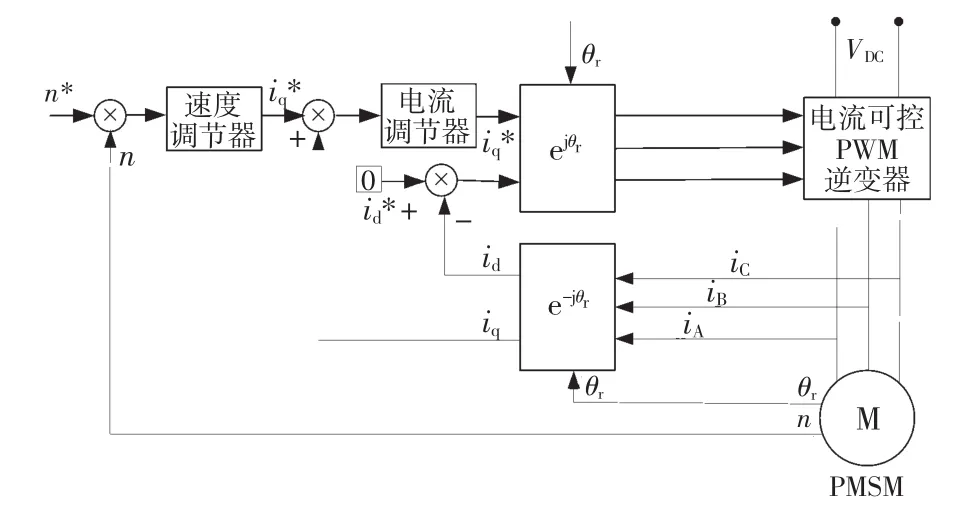
图1 PMSM传统矢量控制系统(M1)框图Fig.1 Traditional vector control(M1)diagram

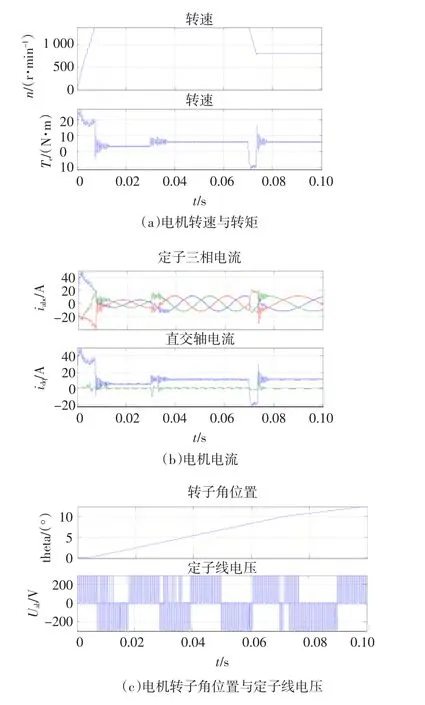
图2 情形一时的电机输出测量Fig.2 Output signal of PMSM in case one

限于篇幅，情形二时仅给出电机转速与转矩的仿真图形如图3所示。

图3 情形二时电机转速与转矩Fig.3 Speed and torque of PMSM in case two

由图3可知，情形二时电机空载低速启动，输出转矩在0.004 s达到稳定，但因为电机是低速空载运转，转矩纹波较大，转速在0.003 s即可达到稳定，超调较小，稳态时转速稳定;在0.03 s负载增加，经0.004 s转矩稳定，稳态时纹波减小，这一过程中转速保持稳定无纹波;在0.07 s给定转速增加，转矩经0.006 s达到稳态，稳态时纹波较小，转速经0.003 s达到稳态，无超调。

2.2 简化矢量控制系统(M2)建模与仿真

为改善系统性能及简化控制，电机的定子三相电流不再进行坐标变换，直接将给定转速与电机转速的差值经速度调节器转变为给定交轴电流iq，而给定直轴电流id恒定为0。经坐标变换后直接与电机定子三相电流比较，其差值作为逆变器的输入，从而控制电势的运行状态。改进后的简化矢量控制系统框图如图4所示。对系统进行实验仿真和定量对比分析见第3节，可知系统性能有所改善。

图4 简化矢量控制系统(M2)框图Fig.4 Simplified vector control(M2)diagram

2.3 转子磁场定向矢量控制系统(M3)建模与仿真

为进一步改善系统性能，根据前述转子磁场定向矢量控制理论及改进系统分析，搭建基于转子磁场定向的简化PMSM矢量控制系统。系统框图如图5所示。对系统进行仿真分析，通过第3节的仿真和定量对比分析可知系统性能得到改善。

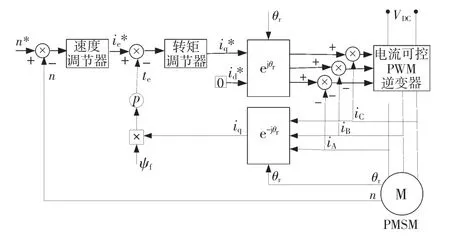
图5 转子磁场定向矢量控制系统(M3)框图Fig.5 Vector control based on rotor flux orientation(M3)diagram

3 系统性能比较分析

为便于对上述3个模型(模型一、模型二、模型三，简写为 M1、M2、M3)的性能进行分析，将3个模型在两种情形下的动态响应过程提取出来绘制于一幅图上，如图6所示。

为便于对3个模型进行定量分析，对仿真结果进行如下处理:针对转速，在启动阶段计算超调率，记为超调率δs;在0.02～0.03 s的稳态时计算实际值与给定值的绝对值平均偏差，记为稳均差et;在0.03s变转矩时计算超调率，记超调率δt;在0.07 s变转速时计算超调率，记为超调率 δυ;在0.05～0.07 s和0.08～0.1 s计算稳均差，分别记为稳均差eυ和稳均差el。得到的转速定量比较如表2所示。

表2 转速定量比较表Table 2 Speed quantitative comparison table

针对转矩，由于在动态时单独地比较最大值并不能反映系统的整体动态性能，因而以动态开始0.005 s时间内的转矩实际值与给定值的绝对值平均偏差来表现整体动态性能。分6个时间窗口［0，0.005］、［0.02，0.03］、［0.03，0.035］、［0.05，0.07］、［0.07，0.075］、［0.08，0.1］计算平均偏差，分别记为动均值 γsd、稳均值 γss、动均值 γtd、稳均值γts、动均值 γυd、稳均值 γυs。其中动均值和静均值的计算如下:设时间窗口［t1，t2］，在该采样窗口内的采样点数为n，采样值矩阵S，给定值S*，具体计算方法见公式(2)。得到转矩定量比较如表3所示。

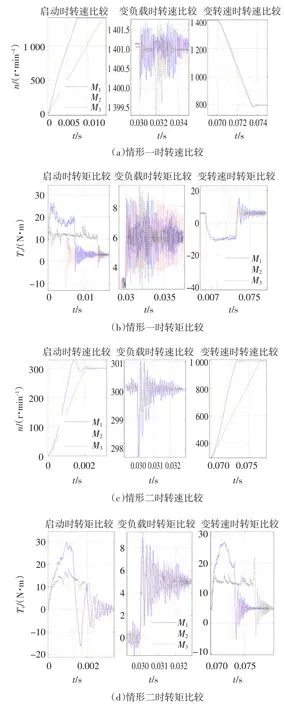
图6 两种情形不同状态输出信号比较图Fig.6 Output signal compare figure on different state

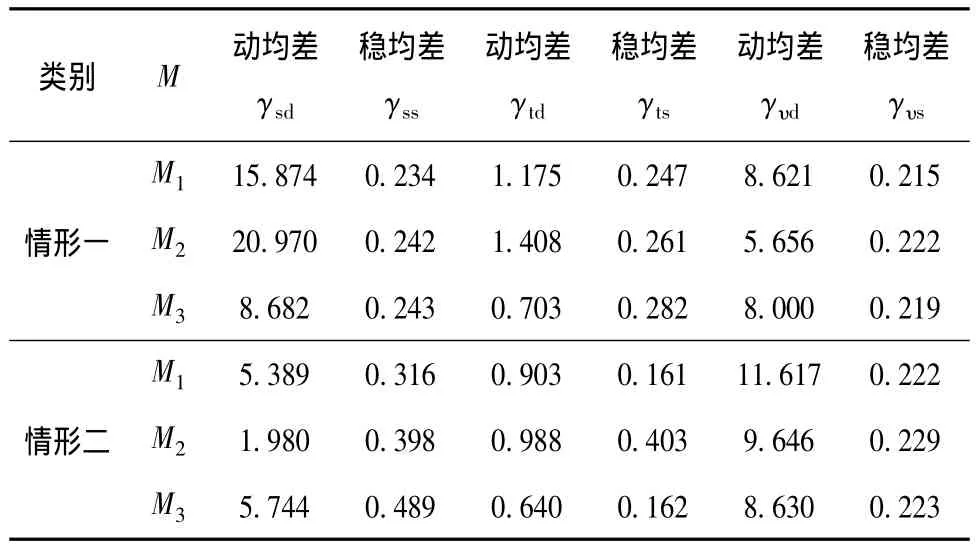
表3 转矩定量比较表Table 3 Torque quantitative comparison table

对3个模型的转速响应分析如下:就转速响应速度而言，M2的响应速度最快，M1次之，M3最慢，但其响应时间均满足控制系统的要求;就超调而言，在启动和变转速时M2的超调明显比M1、M3大，但在转矩变化时其超调最小;就负载扰动而言，3个模型受负载扰动影响相当，但M3恢复稳态所需时间最短，注意到在情形二时系统由空载加载，M2的超调为0.39%，约为M1、M3的(均为0.76%)一半，说明M2空载特性较好。

对3个模型的转矩响应分析如下:就转矩响应速度而言，M2在启动和变转速时的响应速度最快，M1次之，M3最慢，其响应时间均满足控制系统的要求，而M3对变负载时的响应最快;就超调而言，M2的带载启动超调最大，达到20.980 N·m，而空载启动时最小，为1.980 N·m;3个模型在情形二时稳均差1较大，这是因为此时电机空载低速运行;在变转矩时M3的动均差2最小，M2最大，但M2最快达到稳态。

综合以上分析，M2在启动、变负载、变转速情况下均具有最快的响应速度，因而适合于对响应速度有严格要求的场合;M3的响应速度在3个模型中最慢，但其转速、转矩的动态超调最小，稳态性能也较好，由于其响应速度已满足一般系统的要求，因而其应用范围最广。

4 结论

本文应用电流直接反馈方式简化经典矢量控制系统繁杂的坐标变换过程，分别建立了简化的矢量控制系统和转子磁场定向电流直接反馈矢量控制系统。通过与经典矢量控制的仿真比较和定量数据对比分析可知，直接电流反馈法不但能够消去Clarke变换的繁杂过程，而且可以保留经典矢量控制的所有特性，并提高了系统的动态响应，完全证明了简化矢量控制法的可行性。

［1］唐任远.稀土永磁电机发展综述［J］.电气技术，2005，4:1－6.TANG Renyuan.Review of rave earth permanent motor development［J］.Electrical Engineering，2005，4:1 －6.

［2］张磊，高春侠.改进型永磁同步电机全速度范围无传感器控制策略［J］.电机与控制学报，2012，16(7):103－110.ZHANG Lei，GAO Chunxia.An improved whole speed region sensorless control theme for permanent magnet synchronous motors［J］.Electric Machines and Control，2012，16(7):103 －110.

［3］NOGUCHI T.Trends of permanent magnet synchronous machine drives［J］.IEEJ Transactions on Electrical and Electronic Engineering，2007，2(2):125 －142.

［4］王德成，林辉.一种基于支持向量机的矢量控制方法及应用［J］.电机与控制学报，2012，16(5):52 －56.WANG Decheng，LIN Hui.Vector control method based on support vector machine and its application［J］.Electric Machines and Control，2012，16(5):52 －56.

［5］李兵强，林辉.面装式永磁同步电机电流矢量直接控制技术［J］.中国电机工程学报，2011，31:288－294.LI Bingqiang，LIN Hui.Direct control of current vector for surface-mounted permanent magnet synchronous motor［J］.Proceedings of the CSEE，2011，31:288 －294.

［6］KAYHAN Gulez，ALI Ahmed Adam，BUZCU I E，et al.Using passive filters to minimize torque pulsations and noises in surface PMSM derived field oriented control［J］.Simulation Modelling Practice and Theory，2007(15):989－1001.

［7］王正，常浩.永磁同步电机矢量控制系统研究［J］.沈阳工业大学学报，2007，39(3):307－311.WANG Zheng，CHANG Hao.Research on vector control system of permanent magnet synchronous motor［J］.Journal of Shenyang U-niversity of Technology，2007，39(3):307 －311.

［8］王成元，夏加宽，孙宜标.现代电机控制技术［M］.北京:机械工业出版社，2008.

［9］许文强.永磁同步电机控制系统的研究［D］.保定:华北电力大学，2010.