D－分割技术确定磁轴承的PID参数鲁棒稳定域

杨益飞， 骆敏舟， 邢绍邦 ， 韩晓新， 李月红， 朱熀秋

(江苏理工学院电气信息工程学院，江苏常州213001;2.中国科学院合肥物质科学研究院，先进制造技术研究所，江苏常州213164;3.江苏大学电气信息工程学院，江苏镇江212013)

0 引言

PID控制方法的参数整定方便，结构灵活，是控制理论中比较成熟控制方法，在工业控制中占据主要的地位。PID控制器应用在实际工业控制中，需要考虑到鲁棒稳定性。PID控制适合于精确数学模型的控制对象，对于受到外界干扰和不确定性的工业控制系统，通过经验调节得到的PID控制器的参数整定无法得出完整的稳定域.HO给出了结合H∞性能设计的PID参数稳定域，实现不确定控制系统的鲁棒稳定性，达到了期望的性能指标［1］。Saeki给出了PID控制的 H∞性能设计的不同方法［2］。L.H.Keel研究了PID参数稳定域的加权灵敏度和鲁棒稳定问题，但没有考虑到系统鲁棒性能［3］。以上方法给出了PID鲁棒稳定域的设计方法，但都没有考虑到被控系统的时滞现象。

时滞常数的变化是工业控制系统模型不确定性变化最为明显，的因素。Silva推导了一阶不稳定时滞系统所有鲁棒PID控制器参数集的算法［4］。对于时滞项逼近误差的存在，多数人采用帕德近似。磁悬浮轴承作为一种典型的本征不稳定系统，对控制器参数非常敏感，对控制器的设计要求十分苛刻，数字控制中附加时延的存在往往造成控制器不能稳定地工作。本文在前人研究时滞系统的PID参数稳定域整定方法的基础上［5－7］，针对存在时滞现象的磁轴承系统受到外界干扰造成不确定性这一特性，仅依靠传递函数的频率响应，选取合适的加性不确定的权函数，然后，基于边界穿越定理和D－分割技术，设计出满足不确定时滞系统的H∞加权灵敏度约束PID参数鲁棒稳定域。这一方法对于很难获得精确数学模型的磁悬浮轴承系统有着一定的实际使用价值。方法简单、直观，仿真和实验结果证明了本文所采用设计方法的有效性。

1 问题描述

研究的控制对象不是精确模型，具有一定的模型化误差。PID控制器参数选择的是否合适，直接决定了闭环控制系统的性能要求。反馈控制系统的PID控制器K(s)和加性不确定的灵敏度函数分别为

式中:kp为比例系数;ki为积分系数;kd为微分系数;

Gp(s)为任意阶线性定常时滞系统频率响应的传递函数

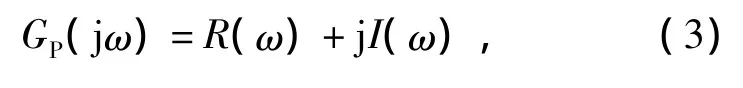
式中 R，I∈R。

X(s)和Y(s)均为有理多项式。设计目的是设计一种在(kp，ki)、(kp，kd)和(ki，kd)平面中的鲁棒稳定域中任选参数，使得控制对象Gp(s)参数发生摄动时，能够使被控对象的动态特性不受不确定性因素的影响，实现反馈控制系统的渐进调节功能。

2 PID参数鲁棒稳定域设计方法

典型的加法不确定性反馈控制系统框图可以由图1表示。其中:w为参考输入信号，y为输出信号，u为控制信号，e为误差信号，K(s)为控制器传递函数，实际控制对象GΔ(s)是具有加性不确定的模型，用加性摄动Δ(s)表示为

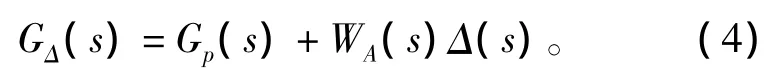
为了确保负载对系统的干扰影响很小，应该考虑输入灵敏度函数的上界。图中，w点到y点的输入灵敏度函数Ua(s)表达为

使用小增益［8］定理，对于加性不确定，得到闭环系统的鲁棒稳定性条件

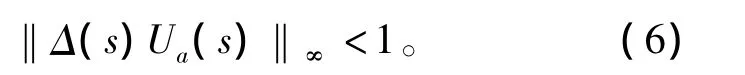
对于反馈控制系统，WA(s)是加法摄动Δ(s)系统期望达到所要求性能的权函数的最大值，表示为

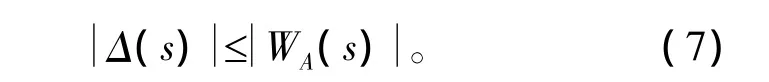
设计目标是找出由此加性不确定性的内部稳定H∞指标的PID参数鲁棒稳定域，这一目标可以通过满足H∞期望指标实现，即

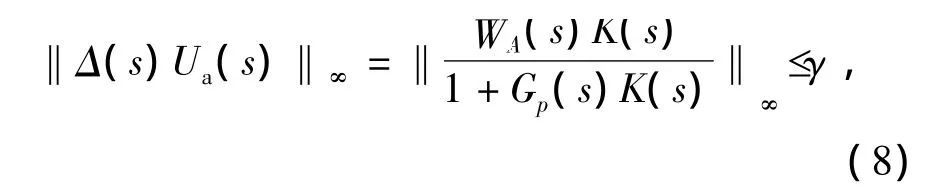
式中，本文的鲁棒性能指标γ=1为有界扰动抑制水平。加权灵敏度约束可以表示为

由式(9)，H∞期望指标重写为

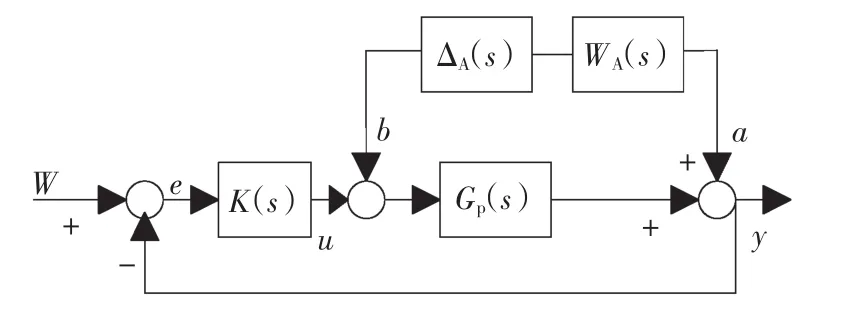
图1 加法不确定性反馈控制系统框图Fig.1 Additive uncertainty feedback control system block diagram

对于每一固定的θA∈［0，2π)，可以找出式(10)的PID控制器参数鲁棒稳定域。系统的闭环特征多项式方程为

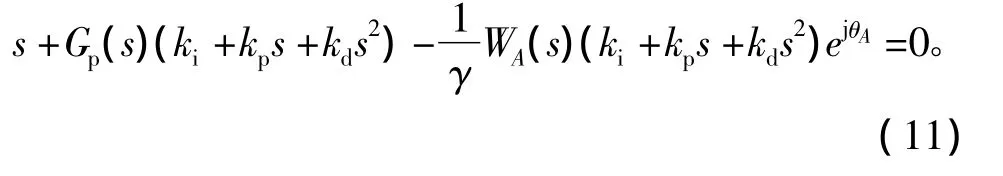
开环左半平面定义为Г，边界表示为

PID参数鲁棒稳定域KΓ是通过位于平面Г中的所有PID参数域的极点定义的，边界表示为∂KΓ。

将s=jω代入到特征多项式(11)中，得

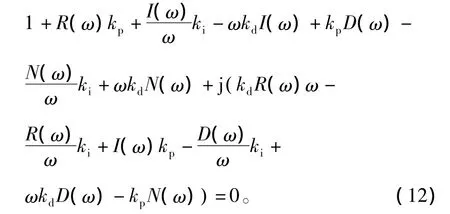
其中:

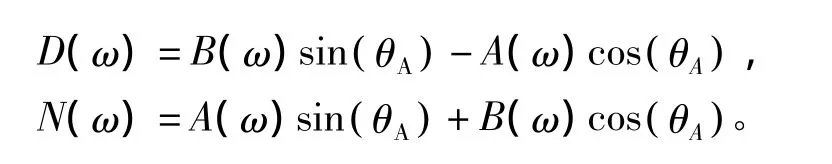
定义式(12)的集合为 K∂Γ，由边界穿越定理［9］可知，K∂Γ包含PID参数鲁棒稳定域的边界∂KΓ。本文说明了一种计算任意阶线性定常时滞系统Gp(s)的方法，

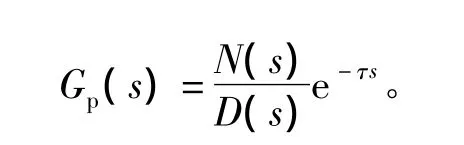
3 PID参数鲁棒稳定域证明

假设1 如果τ恒等于0，则Gp(s)K(s)是严格正则的，如果τ不等于0时，即是正则的。并且进一步假设Gp(s)在虚轴没有零点。

以下证明 PID 控制器(kp，ki)、(kp，kd)(ki，kd)平面的参数鲁棒稳定域。

1)定理1 kd为(kp，ki)平面的参数鲁棒稳定域上的固定值，对于0﹤ ω﹤∞，K∂Γ包含奇异边界线ki=0和以下方程所给定的非奇异边界线曲线

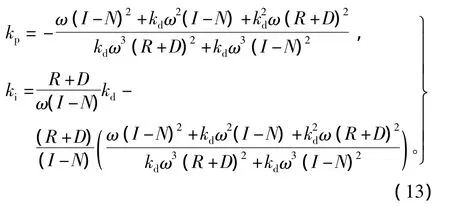
证明 令式(12)的实部和虚部等于零，可得

由D－分割技术［6］可知，鲁棒稳定域边界包括奇异边界(ω=0，ω=∞和非奇异边界(0＜ω＜∞)。当ω =0 和 θA∈［0，2π)时，方程变为 Gp(0)ki—(1/γ)WA(s)ki=0，由式(13)可得ki=0，kp是任意的。当ω=∞和θA∈［0，2π)时，由假设1得知，此时方程无解.综合以上分析可得(kp，ki)平面的参数非奇异稳定域。当0＜ω ＜∞和 θA∈［0，2π)时，此时方程有唯一连续解曲线，因为GP(S)在虚轴没有零点，比如，R2+I2=|Gp(jω)|2≠0，由式(14)可以求解出满足鲁棒性的参数非奇异稳定域的边界线为式(13)。根据式(14)得出雅克比矩阵为

当J＞0时，稳定边界的左侧沿着w增大的方向为参数稳定域，非奇异边界线左侧的不稳定闭环极点少于右侧。反之，当J＜0时，稳定边界的右侧沿着w增大的方向为参数鲁棒稳定域，非奇异边界线右侧的不稳定闭环极点少于左侧［6，10］。式(15)总是小于0，因此沿着w增大方向的右侧确定为参数鲁棒稳定域。

2)(kp，kd)平面的参数鲁棒稳定域的求解类似于定理1关于(kp，ki)平面的参数鲁棒稳定域的方法。设定ki是一固定值。令式(12)的实部和虚部等于零，可得到

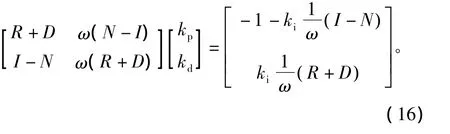
当0＜ ω ＜∞和 θA∈［0，2π)，(kp，ki)参数鲁棒稳定域由以下曲线得出

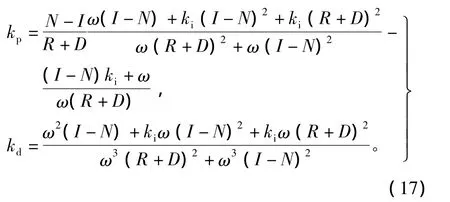
方程(16)中的雅克比矩阵表示为

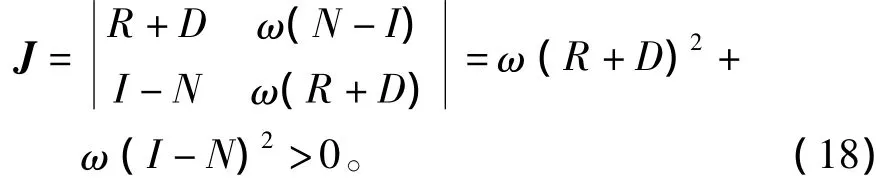
由式(18)可知，J总是大于0，因此沿着w增大方向的左侧确定为(kp，kd)平面的参数鲁棒稳定域。

3)kp已知时，当0＜ω ＜ ∞和 θA∈［0，2π)，由文献［7］得知，(ki，kd)平面的参数鲁棒稳定域是一组直线相交的凸多边形，这组直线表示为kd=a ki+b。取(kp，ki)平面和(kp，kd)平面上对应于 kp的 kd与 ki，便可确定(a，b)值，从而得出(ki，kd)平面的非奇异参数鲁棒稳定域的边界K∂Γ。

4 主动磁轴承的数学模型

主动磁轴承是利用主动可控的电磁力悬浮转子的无接触支承方式，由功放、电磁铁转子和位移传感器组成，径向对象如图2所示。功放将控制电压转换为控制电流，驱动电磁铁产生电磁力悬浮转子，位移传感器检测出转子偏离参考点的位移。

图2 径向磁轴承控制框图Fig.2 Radial magnetic bearing control block diagram

功放电路通常可用一阶低通滤波线性模型来近似，其传递函数为

其中，gwlpf为功放低通算子。

以径向磁轴承为对象是，对磁轴承在工作点平衡位置，通过局部线性化得到模型为

位移传感器的带宽很高，用比例环节描述

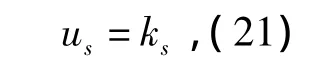
磁轴承的数字控制时延可以表示为［11］

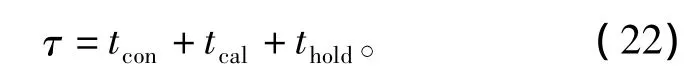
其中:τ为滞后时间常数;tcon为A/D转换时间;thold为零阶保持器延迟时间;tcal为控制算法运算执行间。

考虑时延的径向磁悬浮转子广义被控对象传递函数可以表示为

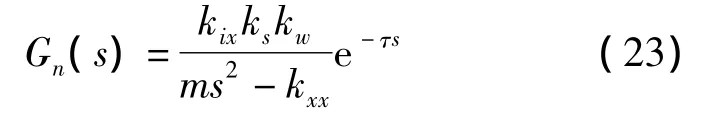
5 算例验证与实验

加性不确定权函数的幅值应该覆盖高频段频率响应的变化。根据上述分析，并结合表1所示的部分样机结构主要参数，再由文献［12］计算式(23)，通过磁轴承的实际控制对象和标称模型的传递函数之差反映到波特图上，合理选取如下加性不确定函数［13］，有

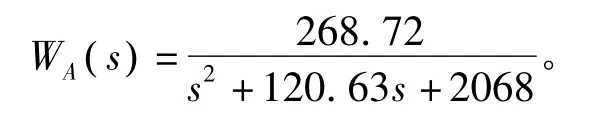
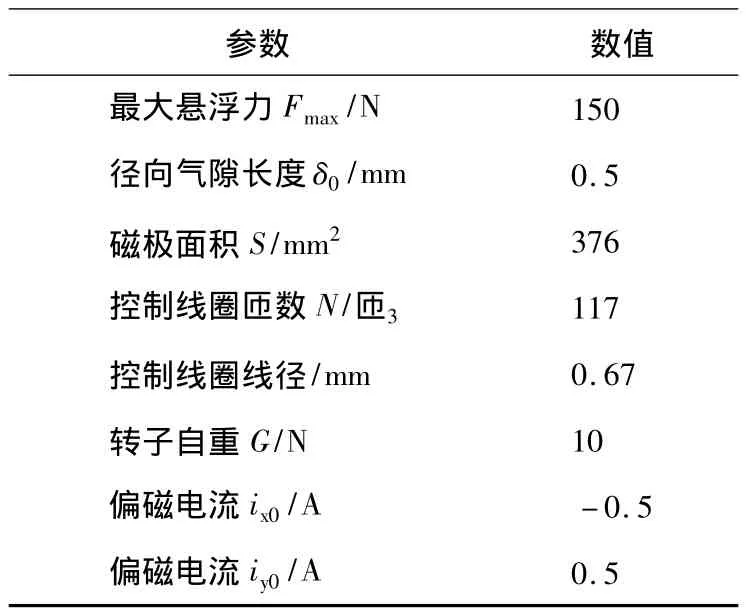
表1 三相交流主动磁轴承结构参数Table 1 Structure parameters of three phases AC active radial magnetic bearing

由定理1，若已知kd=0.2，根据式(13)，当w 增大时，非奇异稳定边界不断向外逐渐变扩大，稳定边界线的右侧比左侧有更少的不稳定极点，即(kp，ki)平面参数鲁棒稳定域位于一组非奇异边界和奇异边界ki=0所包围的区域。(kp，ki)平面的参数鲁棒稳定域如图3所示，从图3中的鲁棒稳定域内外分别取一点 K1和 K2，有

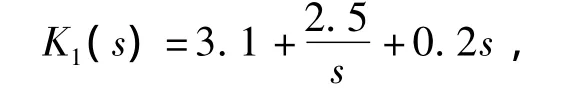
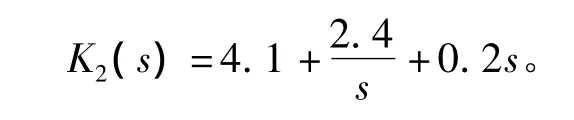
代入式(13)中，从图4可知

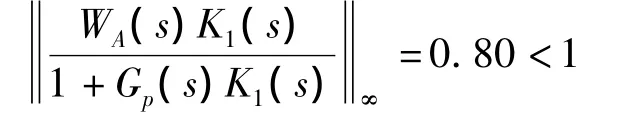
和

满足PID控制器设计的期望指标。图4表明了文中算法的正确性。

图3 (kp，ki)平面的鲁棒稳定区域Fig.3 Robust stability region in(kp，ki)plane

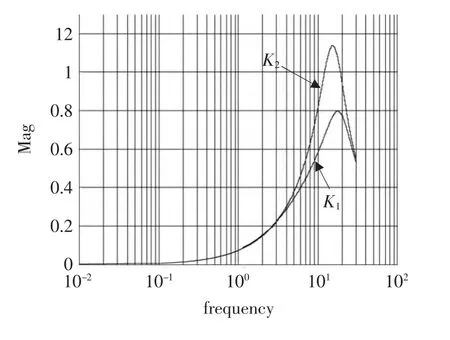
图4 (kp，ki)平面的幅频特性Fig.4 Magnitude-frequency characteristics in(kp，ki)plane

若已知ki=0.5，根据式(17)，得到满足 H∞期望指标式(10)的(kp，kd)平面的参数鲁棒稳定域如图5所示。为了验证这一结果，从图5中的鲁棒稳定域内外各任选一点K3K4，PID控制器为

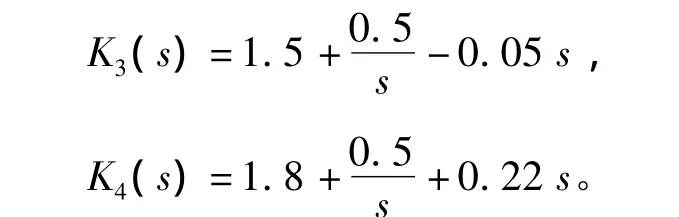
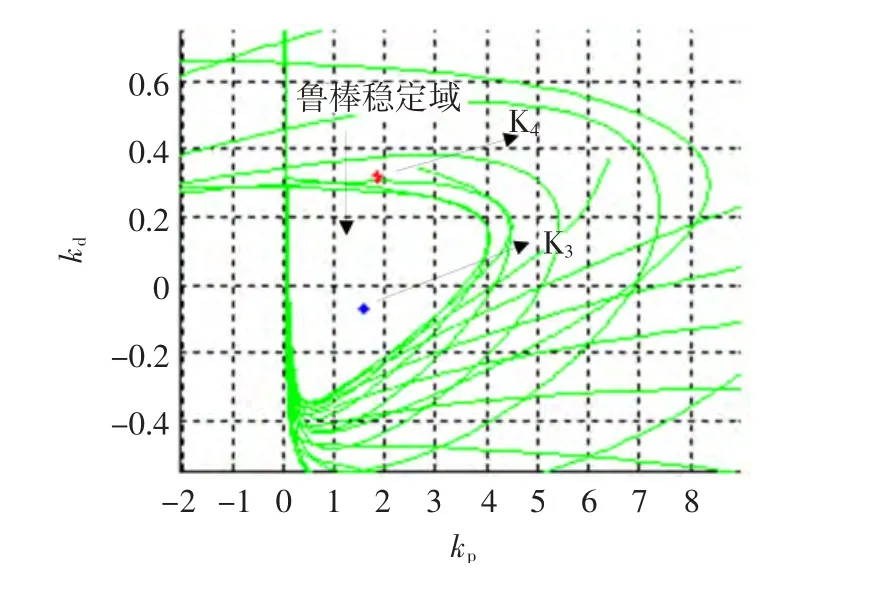
图5 (kp，kd)平面的幅频特性Fig.5 Robust stability region in(kp，kd)plane

图6 (kp，kd)平面的幅频特性Fig.6 Magnitude-frequency characteristics in(kp，kd)plane

由图3和图5鲁棒稳定域可以确定对应于kp的ki和kd，本文取kp=0.1，根据构成凸多边形的一组直线方程kd=a ki+b，求解其中的(a，b)值。由上述直线方程和奇异边界ki=0得到了满足H∞期望指标式(10)的(ki，kd)平面参数鲁棒稳定域如图7所示。

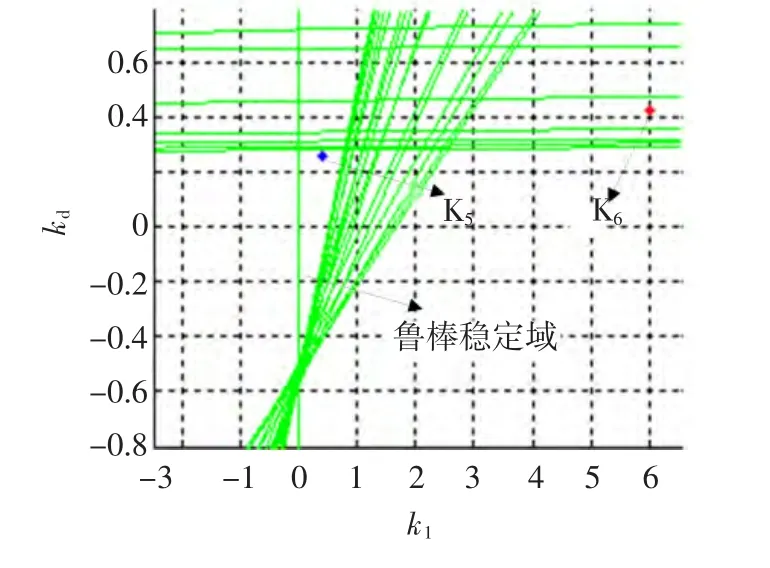
图7 (ki，kd)平面的鲁棒稳定区域Fig.7 Robust stability region in(ki，kd)plane

从图7中的鲁棒稳定域内外任选一点K5和K6验证该指标，PID控制器为

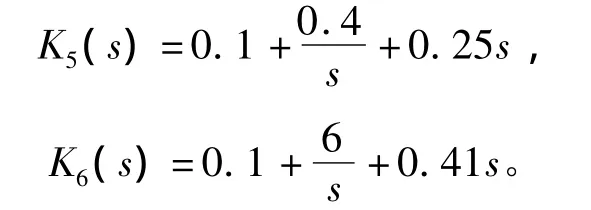
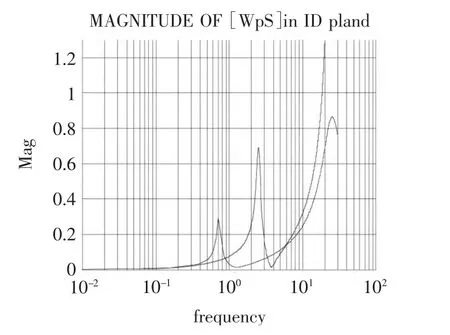
图8 (ki，kd)平面的幅频特性Fig.8 Magnitude-frequency characteristics in(ki，kd)plane

给出了转子一端的径向二自由度主动磁轴承的数字控制系统，径向采用电流跟踪型逆变器提供控制电流。图9为交流二自由度主动磁轴承控制框图，位移传感器检测出转子的径向位移与参考位移比较，误差通过分散控制器调节得到理想的控制电流参考信号，径向电流控制信号与偏置电流相叠加后经过2/3变换成理想的三相交流参考电流信号与反馈电流信号进行滞环比较控制逆变器，由三相逆变器来驱动控制线圈，从而改变控制磁通，以产生期望的悬浮力。通过位移接口电路将转子位移传感器输出电压信号调整为0.2～2.8 V。因此当三相交流主动磁轴承转子位于平衡位置时，输出位移电压信号约为1.5 V。以位于图3稳定域中的PID参数为例(kp=3.1，ki=2.5，kd=0.2)，可以得到实验波形如图10所示。

图9 交流二自由度径向磁轴承控制框图Fig.9 Two-degree-of-freedom radial magnetic bearing control block diagram

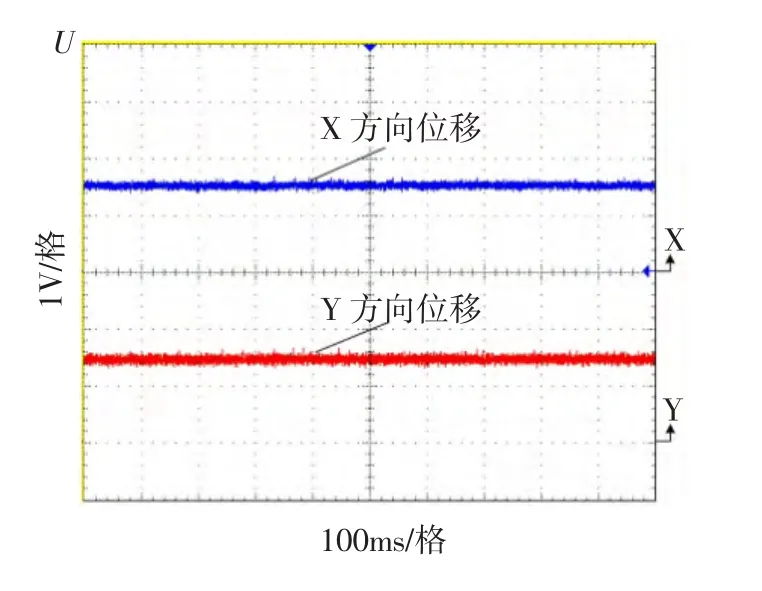
图10 三相交流主动径向磁轴承转子稳定悬浮曲线Fig.10 Three phases AC active radial magnetic bearing-Rotor stable suspension curve

从图10可以看出，转子x和y方向位移响应曲线在1.5 V上下波动，即实现了转子径向方向稳定悬浮控制。图11和图12分别为转子在稳定悬浮时，转子在x方向和y方向受到干扰力时的实验波形。从图11和12中可以看出转子在稳定悬浮时，给转子在x方向和y方向分别施加一个干扰力，转子偏离平衡位置，当干扰力消失后，转子迅速回到平衡位置，实现稳定悬浮。

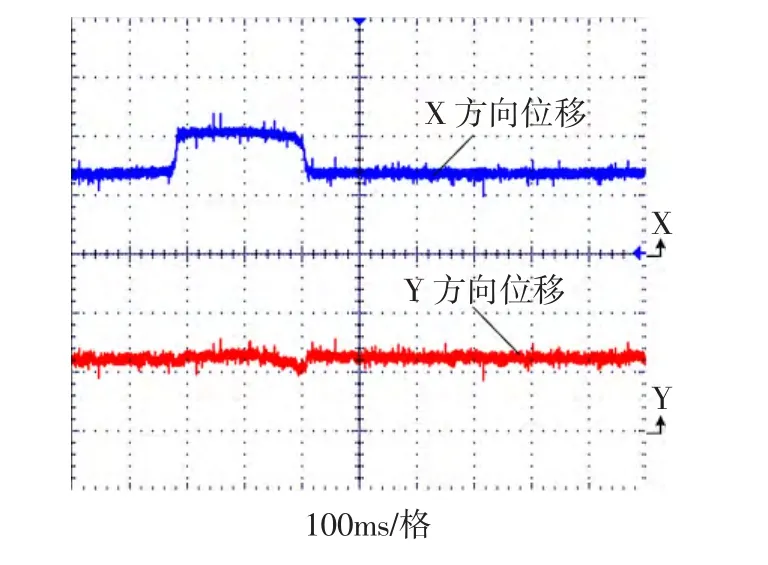
图11 x方向受到扰动时位移波形Fig.11 Displacement wave of x-direction with disturbance

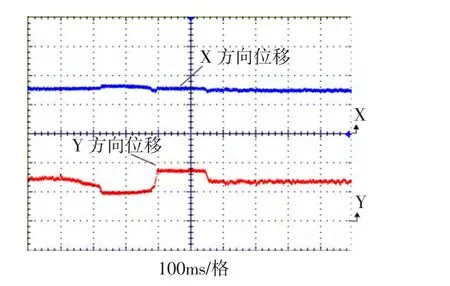
图12 y方向受到扰动时位移波形Fig.12 Displacement wave of y-direction with disturbance

另外，选取以位于图5稳定域中的PID参数为例(kp=1.5，ki=0.5，kd= －0.05)为例，观察转子的位移波形变化情况。图13和图14所示分别为x方向和y方向受到扰动时的位移波形图。当对x方向施加干扰，y方向基本不受影响，并且这两个方向均能恢复到平衡位置;对y方向施加干扰，x方向受到的扰动较小，并且x方向和y方向均能恢复到平衡位置状态。

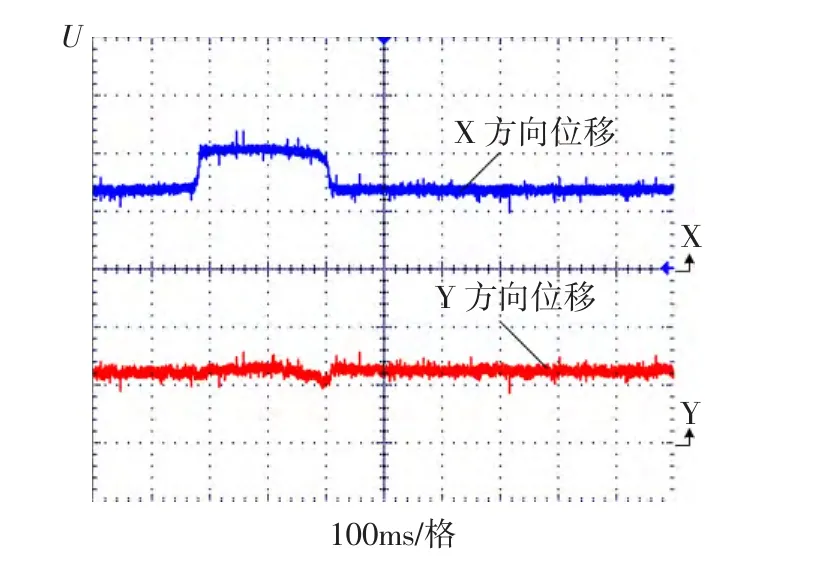
图13 x方向受到扰动时位移波形Fig.13 Displacement wave of x-direction with disturbance

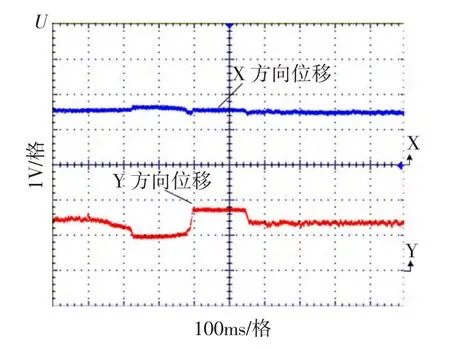
图14 y方向受到扰动时位移波形Fig.14 Displacement wave of y-direction with disturbance

最后，选取以位于图7稳定域中的PID参数为例(kp=0.1，ki=0.4，kd=0.25)为例，观察转子的位移波形变化情况。图15和图16所示分别为x方向和y方向受到扰动时的位移波形图。当只对x方向和y方向其中一个方向施加扰动后，另一个方向受到的扰动较小，并且x方向和y方向均能恢复到平衡位置状态。对于图16，x方向和y方向虽然都稳定悬浮了，但是离平衡位置还差一点，其原因在于所选取的图7稳定域中的PID参数临近边界，其效果没有以上实验好。

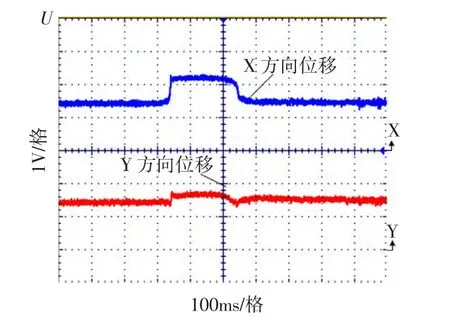
图15 x方向受到扰动时位移波形Fig.15 Displacement wave of x-direction with disturbance

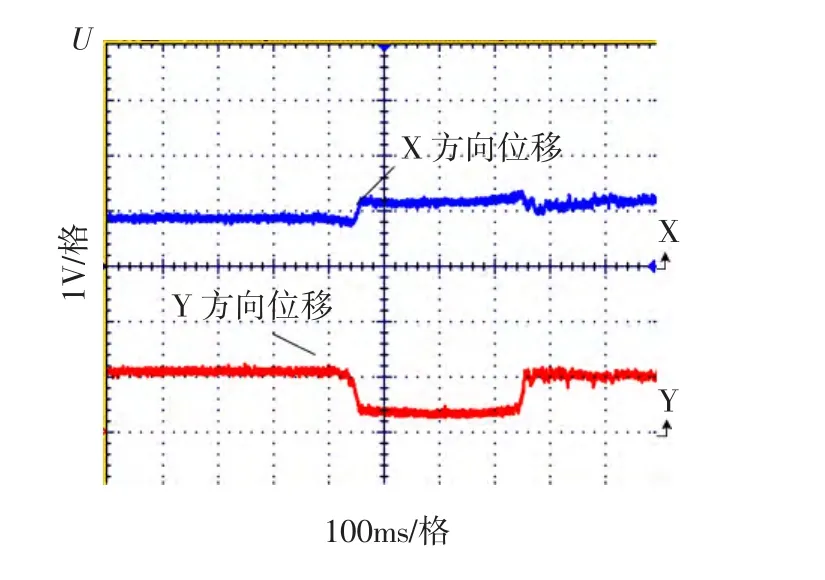
图16 y方向受到扰动时位移波形Fig.16 Displacement wave of y-direction with disturbance

以上实验结果表明使用本文的控制算法时，系统起浮过程平稳，阻尼合适，响应性好，抗干扰性强，并具有良好的动态性能。

7 结论

本文给出一种快速计算径向磁轴承的鲁棒PID控制器参数稳定域的方法。该方法的特点是计算简单，结果可靠.根据边界穿越定理并结合小增益定理，在鲁棒稳定域中任选PID参数，可以使系统稳定并满足鲁棒性能约束条件。该方法可推广到其他有时滞或者无时滞的控制系统中，并且对于控制系统数学模型的精确度要求不高，为参数调节带来的方便，具有一定的普遍性和实用性。

［1］HO M T.Synthesis of H∞PID controllers:A parametric approach［J］.Automatica，2003，39(6):1069 －1075.

［2］SAEKI M.Properties of stabilizing PID gain set in parameter space［J］.IEEE Transactions on Automatic Control，2007，52(9):1710－1715.

［3］KEEL L H，BHATTACHARYYA S P.Controller synthesis free of analytical models:three term controllers［J］.IEEE Transactions on Automatic Control，2008，53(6):367 －372.

［4］SILVA G J，DATTA A，BHATTACHARYYA S P.On the stability and controller robustness of some popular PID tuning rules［J］.IEEE Transactions on Automatic Control，2003，48(9):1638－1641.

［5］方斌.时滞系统PID控制器参数稳定域的实现［J］.电子科技大学学报，2011，40(3):411 －417.FANG Bin.Realization of PID controller parameter stable regions for time delay systems［J］.Journal of University of Electronic Science and Technology of China，2011，40(3):411 － 417.

［6］林示麟，欧林林，俞立.无模型SISO时滞系统的PID参数稳定域研究［J］.控制理论与应用.2009，26(4):443－445.LIN Shilin，OU Linlin，YU Li.Stability regions of PID parameters for model-free SISO systems with time delay［J］.Control Theory ＆Applications.2009，26(4):443 －445.

［7］方斌.基于稳定裕量的二阶时滞系统PID控制器参数稳定域［J］.信息与控制.2011(02):255－273.FANG Bin.Second-order time delay system stable regions of PID controller parameter based on stability margins［J］.Information and control，2011，40(2):192 －197.

［8］ACKERMANN J ，BARTLETT A，KAESBAUER D，et al.Robust control systems with uncertain physical parameters［M］.Berlin，Germany:Springer-Verlag Press，1993.

［9］LII G H，CHANG C H，HAN K W ，Analysis of robust control systems using stability equations［J］.Control Systems and Technology，(1993)，1:83 －89.

［10］KWAKERNAAK H.Robust control and H∞optimization tutorial paper［J］.Automatica，1993，29(2):255 － 273.

［11］李德广，刘淑琴，磁悬浮轴承数字控制的稳定性分析及预补偿算法［J］.电工技术学报，2011，26(6):108－112.LI Deguang，LIU Shuqin.Stability analysis of the AMB digital control system and its prediction compensatory Algorithm［J］.Transactions of China Electrotechnical society.2011，26(6):108－112.

［12］朱熀秋，黄振跃，阮颖，等.交流主动磁轴承电主轴线性二次型最优控制［J］.电机与控制学报，2012，16(10):71－78.ZHU Huangqiu，HUANG Zhenyue，RUAN Ying，et al.Linear quadratic optimal control of electric spindle supported by AC magnetic bearings［J］.Electric Machines and Control，2012，16(10):71－78

［13］彭程，王永.柔性梁降阶H∞控制实验研究［J］.振动与冲击，2007，26(10):64－67.PENG Cheng，WANG Yong.An experi mental study on reduced order H∞control of a flexible beam［J］.Journal of Vibration and Shock，2007，26(10):64 －67.