双馈风机虚拟惯量控制对传动系统扭振影响

章德， 刘锋， 梅生伟， 刘思宇

(1.国网湖南省电力公司经济技术研究院，湖南长沙410000;2.清华大学电力系统国家重点实验室，北京100084;3.北京理工大学 自动化系，北京100081)

0 引言

风力发电作为目前技术最成熟、最具规模开发条件的可再生能源发电形式，近年来在全球范围内迅猛发展。截止到2012年底，全球风电累计装机容量达到了282.5 GW，中国的风电累计装机容量则达到了75.324 GW，继续居世界第一位［1］。随着风电在电力系统中的渗透率不断增加，分析和研究风电接入对电力系统安全稳定运行的影响变得尤为重要。其中，考虑大规模风电接入对电力系统频率控制的影响是重要课题之一［2－3］。

双馈风电机组由于风能捕获效率高、机械应力小以及有功无功解耦控制等特点，近年来逐渐成为风电市场上的主流机型之一。然而，由于双馈风电机组的转子经背靠背的双向电压源变换器与电网相连，其转子转速与电网频率解耦，因此对系统惯性几乎没有贡献，一般也不参与系统的频率控制。随着基于双馈风电机组的风力发电大规模接入电网，一方面，一部分传统同步发电机组可能被取代;另一方面，传统同步发电机组在发电组成中所占比例也会越来越小。这将有可能使得系统相对惯量下降、频率控制能力减弱，从而导致频率不合格，甚至出现频率不稳定问题。

为了解决含大规模风电电力系统的有功/频率控制问题，国内外学者已经对双馈风电机组如何参与电力系统频率控制、维持系统频率稳定进行了一系列研究，目前主要有以下两种方案:

1)备用功率控制。即通过控制桨距角或调整功率－转速最优运行曲线来实现风电机组减载运行，从而留出一定的有功调节裕度来参与电力系统频率控制［4－8］。

2)虚拟惯量控制。对于同步发电机组，当系统频率降低或升高时，其转子将相应减速或增速，通过动能与电能的转化来抑制频率波动，此即同步发电机组的惯性响应(Inertia Response)。虽然双馈风电机组的转子转速与电网频率相互解耦，但其旋转元件(包括风轮、传动轴和发电机转子等)仍然储存了可观的动能。因此，可以在双馈风电机组的控制系统中引入系统频率响应环节，从而当系统频率变化时通过其旋转元件中储存的动能和电能的相互转化，在较短时间内增加或减小风电机组的有功出力，以参与系统频率控制［4、9－14］。由于此种频率控制方案启发于同步发电机组的惯性响应，因此可称为“虚拟惯量控制(Inertia Response Control，IRC)”。

双馈风电机组虚拟惯量控制通过旋转元件中储存的动能来参与电力系统频率控制，因此有必要考察虚拟惯量控制过程中传动系统的动态行为。目前已有文献主要采用比例微分控制(PD控制)来实现双馈风电机组的虚拟惯量控制，其传动系统一般采用1质块等效模型。然而，采用传动系统1质块模型可能不能准确地反映风电机组在电力系统暂态过程中动态行为。例如，文献［15－17］采用传动系统2质块或3质块模型，从而更加准确地分析了风电机组暂态稳定性。同时，风电机组本身也可能会产生传动系统扭振。文献［18］建立了传动系统3质块模型，计算出其固有振荡频率，并通过时域仿真指出电网故障可能激发风电机组的传动系统扭振。文献［19］采用传动系统2质块模型，指出当风电机组励磁控制参数配合不当时将产生电气负阻尼，从而导致传动系统扭振。文献［20］指出如果双馈机组所选择的控制策略不能提供有效的电气阻尼的话，则在小扰动或暂态故障下激发的传动系统扭振将得不到有效抑制，从而导致机组转速失稳。结合文献［19］和［20］，为了抑制风电机组的传动系统扭振，一方面必须在风电机组设计时选取适当的控制策略及参数，另一方面也可以通过附加阻尼控制器来抑制传动系统扭振。文献［21］提出了一种基于自抗扰控制技术的双馈风电机组传动系统扭振的抑制策略，可以在不影响机组发电量的前提下有效抑制传动系统扭振。文献［22］和［23］分析了基于带通滤波器的扭振阻尼控制器和基于卡尔曼滤波和状态反馈的扭振阻尼控制器对传动系统扭振的抑制作用，并对其控制性能进行了比较。上述文献都没有考虑风电机组虚拟惯量控制过程中传动系统的动态行为。然而，风电机组虚拟惯量控制需要快速改变其输出的电磁功率或转矩，从而使得传动系统输入的机械转矩和输出的电磁转矩产生不平衡，因此有可能导致其传动系统扭振，造成传动系统零部件疲劳损伤，长此以往甚至引起齿轮箱等部件发生故障。

综上，在双馈风机虚拟惯量控制过程中，一方面应该指出如何选择传动系统的模型，才能准确地分析虚拟惯量控制对传动系统动态行为的影响;另一方面，应考虑设计扭振阻尼控制器以有效抑制虚拟惯量控制可能引起的传动系统扭振。因此，本文分析了双馈风机虚拟惯量控制对传动系统扭振影响的机理，同时比较了不同模型下传动系统在双馈风机虚拟惯量控制过程中动态行为。并在此基础上设计了扭振阻尼控制器，以有效抑制双馈风机虚拟惯量控制所引起的传动系统扭振。

1 双馈风电机组传动系统建模

1.1 双馈风电机组基本结构

双馈风电机组的基本结构如图1所示，其定子侧直接与电网相连，转子侧经背靠背的双向电压源变换器与电网相连。双馈风电机组通过对转子侧变换器的控制实现定子侧有功功率和无功功率的解耦控制，通过对网侧变换器的控制来稳定直流母线电压以及调节其与电网交换的无功功率［24－26］。当输出有功在额定功率以下时，风电机组一般采用最大功率点跟踪控制(MPPT控制)，其输出功率基本不受电网频率变化的影响。

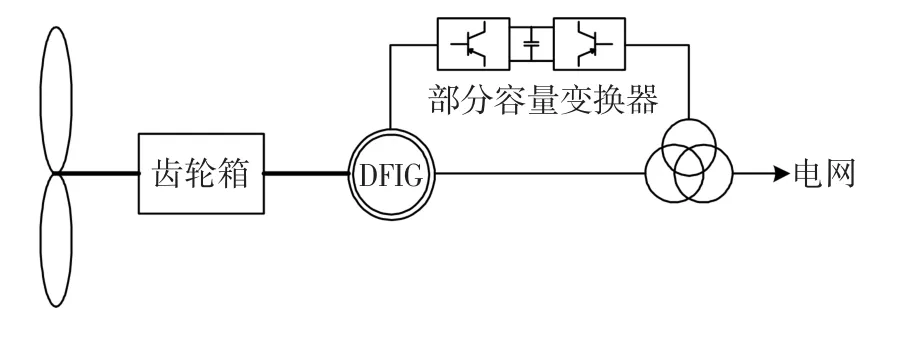
图1 双馈风电机组基本结构Fig.1 Structure of DFIG-Based WTG

1.2 传动系统建模

双馈风电机组的传动系统由叶片、轮毂、低速传动轴、齿轮箱、高速传动轴和发电机转子等构成。传动系统的模型在文献［15］中已有比较详细的介绍，这里只简单给出3质块、2质块和1质块模型。

1.2.1 传动系统3质块模型

传动系统的3质块模型如图2所示，将风力机叶片等效为质块1，将轮毂、低速传动轴等效为质块2，将齿轮箱、高速传动轴和发电机转子等效为质块3。将低速轴各量折算到高速轴，用标幺值表示的传动系统3质块模型的动力学方程为

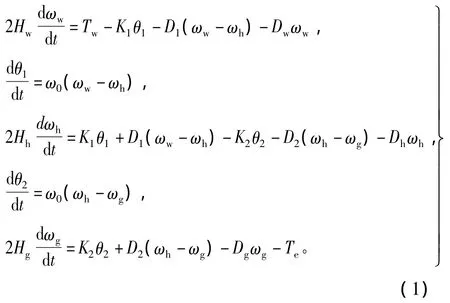
其中，Hw、Hh和Hg分别为质块1、质块2和质块3的惯性时间常数，ωw、ωh和ωg分别为3个质块的电角速度，ω0=2πf0(f0为电网额定频率)系统电角速度基值，θ1和θ2为质块1和质块2、质块2和质块3之间的相对角位移，K1和D1分别为质块1和质块2之间的等效刚度系数和等效阻尼系数，K2和D2分别为质块2和质块3之间的等效刚度系数和等效阻尼系数，Dw、Dh和Dg分别为三个质块的自阻尼系数，Tw和Te分别了风力机的机械转矩和发电机的电磁转矩。

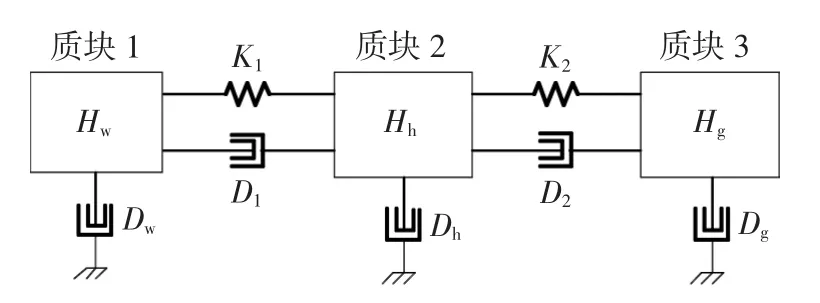
图2 双馈风电机组传动系统3质块模型Fig.2 Schematic diagram of 3-mass model of drive train of DFIG-Based WTG

1.2.2 传动系统2质块模型

传动系统的2质块模型如图3所示，将叶片、轮毂和低速传动轴等效为一个质块，将齿轮箱、高速传动轴和发电机转子等效为另一个质块。将低速轴各量折算到高速轴，用标幺值表示的传动系统2质块模型的动力学方程为

其中，Ht和Hg分别为质块1和质块2惯性时间常数，ωt和ωg分别为2个质块的电角速度，θ为两个质块的相对角位移，K和D分别为两个质块之间的等效刚度系数和等效阻尼系数，Dt和Dg分别为两个质块的自阻尼系数。

图3 双馈风电机组传动系统2质块模型Fig.3 Schematic diagram of 2-mass model of drive train of DFIG-Based WTG

必须指出的是，传动系统2质块模型是从3质块模型导出的，其相关参数由下述公式得出［15］:此外，忽略3质块模型中质块1和质块2之间的互阻尼，则 D=D2。

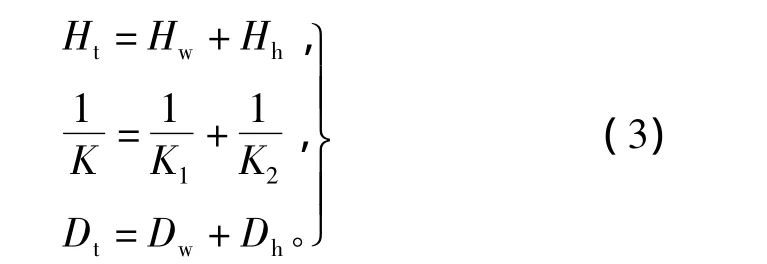
1.2.3 传动系统1质块模型

传动系统1质块模型将叶片、轮毂、低速传动轴、齿轮箱、高速传动轴和发电机转子等效为一个质块，其动力学方程为

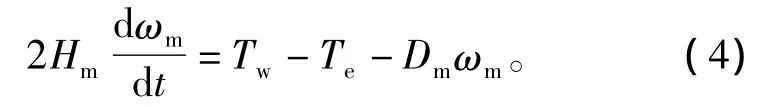
其中，Hm=Hw+Hh+Hg为质块的惯性时间常数，Dm=Dw+Dh+Dg为质块的自阻尼系数，ωm为质块的电角速度。

2 双馈风电机组虚拟惯量的PD控制

双馈风电机组虚拟惯量的PD控制(PD－Based IRC)的基本结构如图4所示。

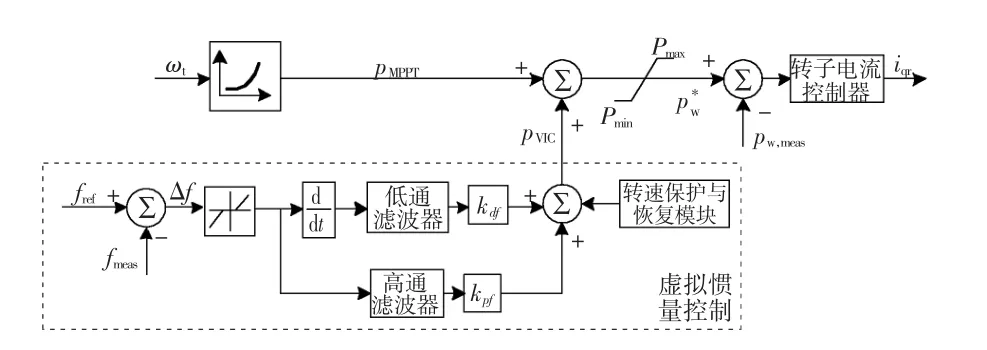
图4 双馈风电机组虚拟惯量的PD控制Fig.4 PD-Based IRC of DFIG-Based WTG

通常情况下，双馈风电机组采用MPPT控制，即控制系统维持最优转速以捕获最大风功率。为了实现风电机组的虚拟惯量控制，在其控制系统中引入了一个附加虚拟惯控制器:其输入是电网参考频率fref与实际测量频率fmeas之差Δf，其输出是有功参考值增量pVIC，其值为

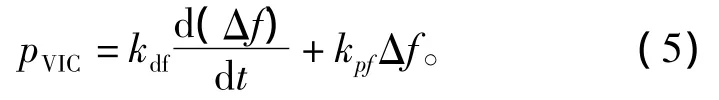
由式(5)可知，虚拟惯量控制输出给风电机组的附加有功参考值增量包括两个部分:1)与频率变化率成正比的有功增量，其控制效果相当于同步发电机组的惯性响应;2)与频率偏移量成正比的有功增量，其控制效果相当于同步发电机组的一次调频。

当电力系统频率发生变化时，风电机组通过虚拟惯量控制可以调整有功功率参考值，从而将旋转元件的部分动能转化为电能，调节其有功出力来参与系统频率控制。值得指出的是，一方面，在风电机组虚拟惯量控制过程中需要防止转子转速超出安全运行范围;另一方面，当系统频率恢复后，风电机组需要恢复到最优转速以实现最大风能捕获。因此一般还需要加入风电机组转子转速保护和恢复模块。

3 双馈风电机组虚拟惯量控制对传动系统扭振影响分析

3.1 传动系统的扭振模式

根据式(1)和式(2)，可以得出传动系统3质块和2质块模型的状态矩阵，进而可以对其进行特征分析，计算出传动系统的扭振模式。传动系统3质块模型的状态矩阵为

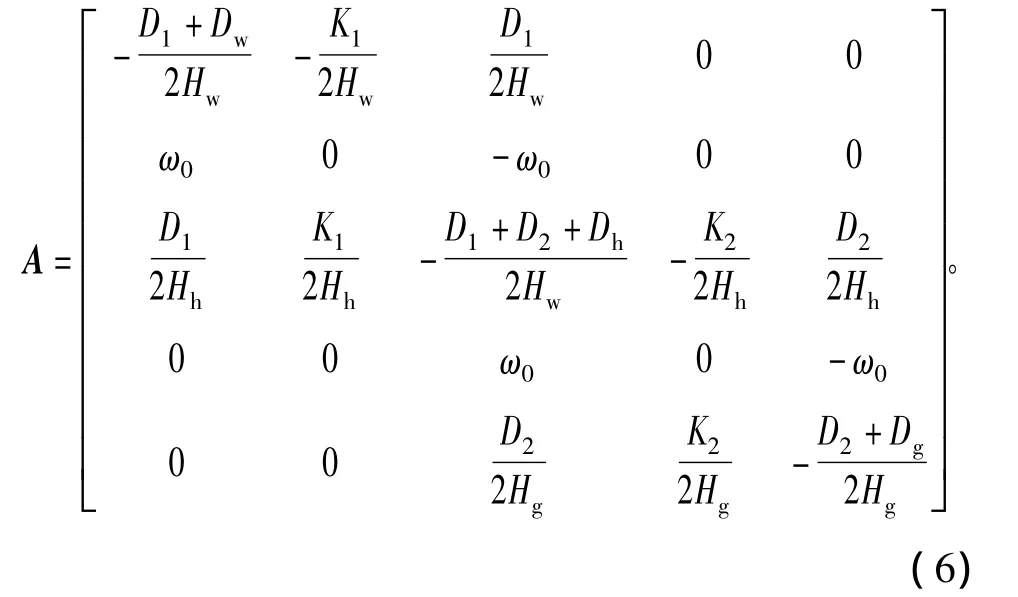
传动系统2质块模型的状态矩阵为

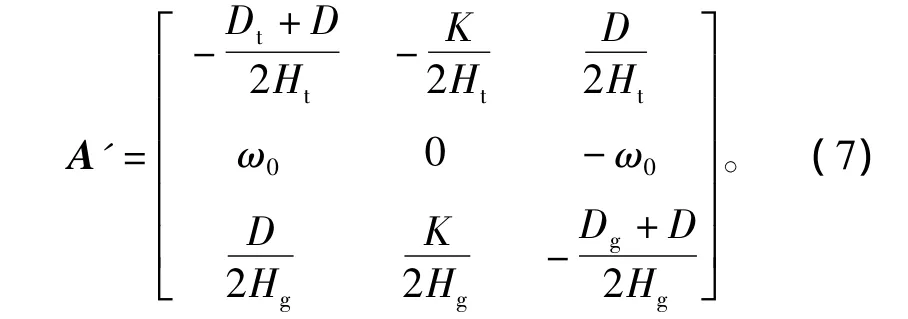
以一个额定功率为2 MW的双馈风电机组为例，其传动系统3质块模型的参数(折算到高速侧)如表1所示。相对应的2质块和1质块模型的参数可以通过第1部分所述方法计算得出。

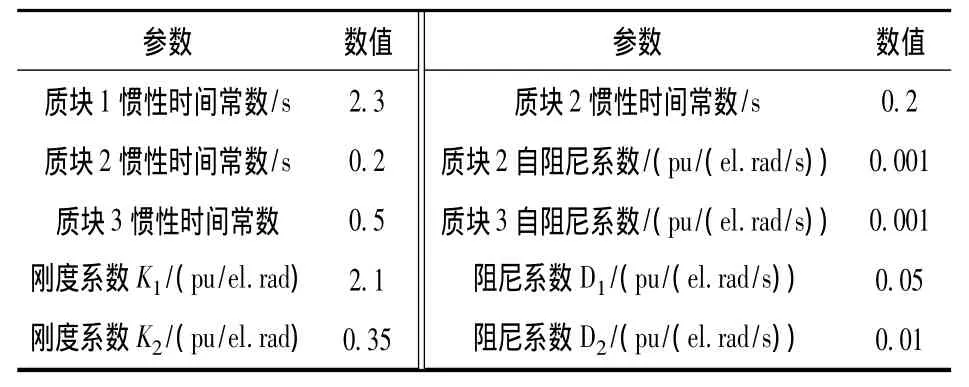
表1 双馈风电机组传动系统参数Table 1 Parameters of drive train of DFIG-Based WTGs

根据表1的数据所计算得出的传动系统扭振模式如表2所示。

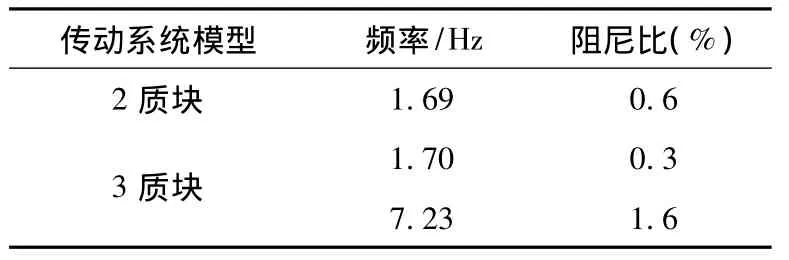
表2 双馈风电机组传动系统的扭振模式Table 2 Torsional modes of drive train of DFIG-Based WTGs

由表2可知，无论是2质块模型和3质块模型，传动系统均存在一个频率约为1.70 Hz的弱阻尼扭振模式，并且该模式与发电机转子转速强相关。

3.2 虚拟惯量控制对传动系统扭振影响的机理

根据式(5)，当电网频率变化时，双馈风电机组虚拟惯量将根据所量测频率(一般为PCC点)的偏差及其变化率来产生附加有功参考值，从而快速改变机组有功出力以参与系统频率控制。由此可知，虚拟惯量控制将在传动系统中引入一个与系统频率变化相关的电磁转矩扰动，其中很可能包含与传动系统固有扭振频率相近的分量。此时，若传动系统本身扭振模式是弱阻尼的(如表2所示)，则虚拟惯量控制可能激发比较明显的扭振。

3.3 附加扭振阻尼控制器的虚拟惯量控制设计

为了抑制双馈风电机组虚拟惯量控制所引起的传动系统扭振，一个比较直接的方法就是增加相应扭振模式的阻尼。因此，可以在控制系统中加入基于双馈发电机转子转速反馈的扭振阻尼控制器，如图5中虚线框所含模块所示。

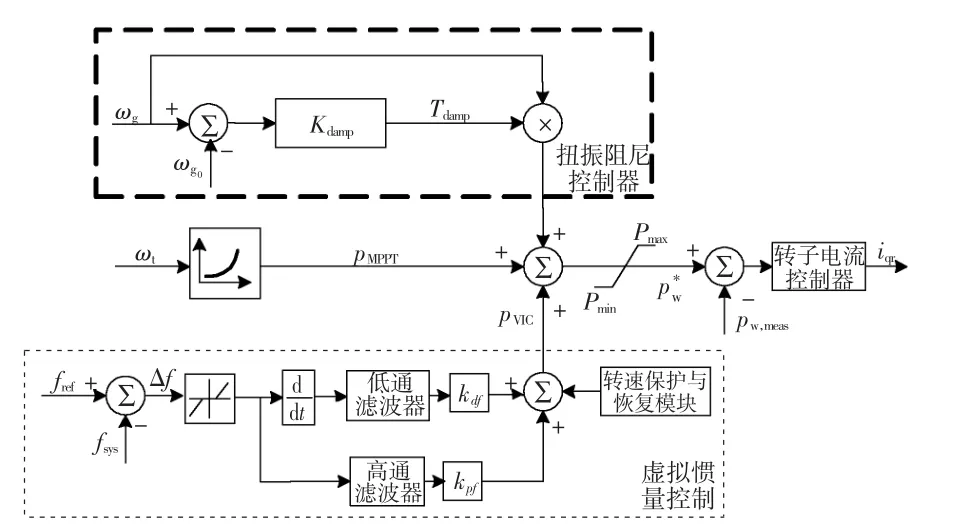
图5 含扭振阻尼控制器的双馈风电机组虚拟惯量控制Fig.5 Inertia Response Control of DFIG-Based WTG including torsional damping controller

所设计的扭振阻尼控制器的输入为双馈发电机转子转速ωg，输出为转矩附加阻尼信号

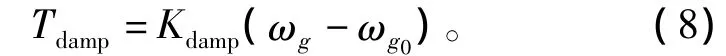
其中，ωg0为电网频率变化之前双馈发电机转子转速，Kdamp为控制器增益。

结合双馈风电机组传动系统2质块和3质块模型的动力学方程可知，上述扭振阻尼控制器作用相当于增加发电机转子的自阻尼，并且Kdamp越大，注入的阻尼也越大。

4 仿真分析

4.1 仿真系统

本文所使用的仿真系统如图6所示，采用PSCAD/EMTDC软件来进行仿真。其中同步发电机G1G2和G3完全相同，额定电压为13.8 kV，额定功率为120 MW，惯性时间常数为3.5 s。所有同步发电机均安装有励磁系统和调速器。在频率变化过程中，同步发电机将有惯性响应和一次调频，但没有考虑二次调频。负荷采用恒功率模型，初始负荷为190 MW。节点1和节点3、节点2和节点3之间的联络线长度均为100 m，线路采用π型等值电路进行仿真，参数为PSCAD/EMTDC默认值。

风电场包含10台2 MW的双馈风电机组，通过变压器从0.69 kV升压到13.8 kV后接入系统。仿真时风电场采用一台容量为20 MW的等值机组代替。风电场风速维持为12 m/s，稳态时对应的发电机转子转速为1.087 pu，风电场有功出力约为15 MW。

图6 仿真系统模型Fig.6 Diagram of test system

双馈风电机组传动系统3质块模型参数(折算到高速侧)如表2所示，其电气参数如表3所示。仿真时双馈风电机组采用电磁暂态详细模型。

在风电场标幺值系统(功率基值取为风电场总额定功率20 MVA，电压基值取为额定相电压幅值)下，双馈风电机组虚拟惯量PD控制器的参数为比例系数kpf=0.06，微分系数为kdf=0.3。同时为了防止双馈风电机组的虚拟惯量控制频繁启停，其控制死区设为49.9～50.1 Hz。电力系统频率超出死区范围后，双馈风电机组启动虚拟惯量控制，其持续时间设为10 s，之后开始转子转速恢复过程。

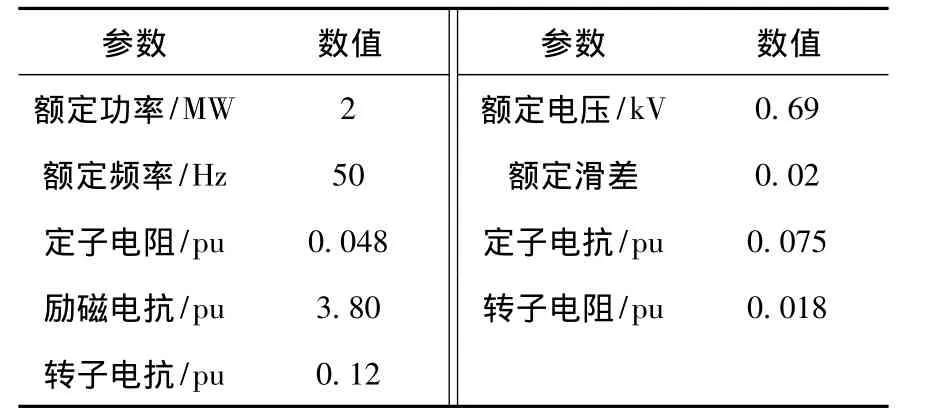
表3 双馈风电机组电气参数Table 3 Electrical parameters of DFIG-Based WTGs

4.2 虚拟惯量控制对传动系统扭振的影响仿真

为了分析双馈风电机组虚拟惯量控制对电力系统频率的支撑效果以及对传动系统扭振的影响，分别对下述4种情况进行仿真。

Case 1:双馈风电机组不提供虚拟惯量控制，传动系统采用1质块模型;

Case 2:双馈风电机组提供虚拟惯量控制，传动系统采用1质块模型;

Case 3:双馈风电机组提供虚拟惯量控制，传动系统采用2质块模型;

Case 4:双馈风电机组提供虚拟惯量控制，传动系统采用3质块模型。

当系统稳定运行后，将节点3上的负荷增加8%(15.2 MW)。图7～图9分别给出了上述4种情况下电网频率、双馈发电机转子转速以及风电场有功出力的时域仿真波形。

由图7可知，当风电场不含虚拟惯量控制时，系统的最低频率约为49.20 Hz。无论传动系统采用1质块、2质块还是3质块模型，双馈风电机组虚拟惯量控制均能将最低频率提高至49.27 Hz。由此可见，传动系统模型并没有影响双馈风电机组虚拟惯量控制的效果。

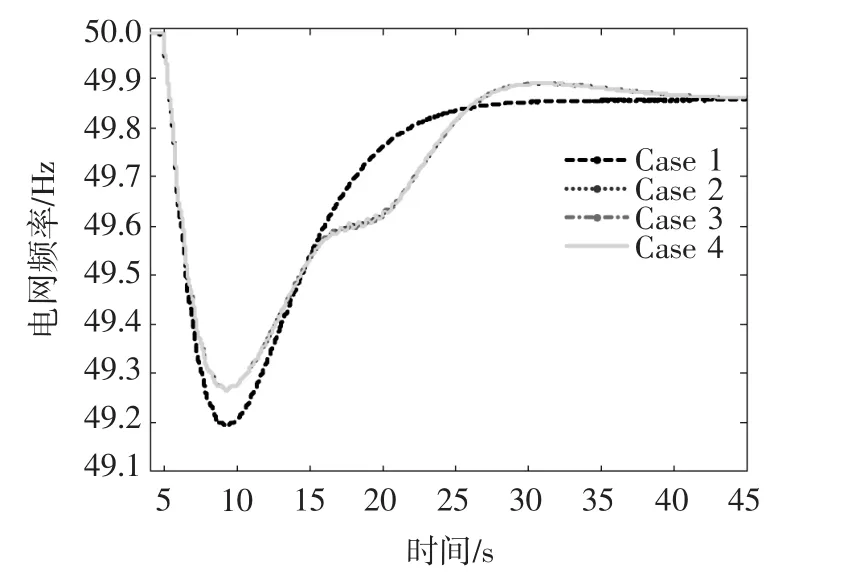
图7 电网频率变化曲线 (Case 1，2，3 and 4)Fig.7 Response of grid frequency(Case 1，2，3 and 4)

由图8可知，双馈风电机组虚拟惯量控制通过降低旋转元件转速以释放动能，来参与系统频率控制。然而，虚拟惯量控制使得传动系统2质块和3质块模型产生了明显的扭振，其频率约为1.7 Hz。并且，由图9可知，当传动系统采用2质块或3质块模型时，风电场有功出力中均包含了频率约为1.7 Hz的振荡分量。此外，2质块和3质块模型的仿真结果基本一致。

通过传动系统采用2质块和3质块模型的仿真结果可知:一方面，双馈风电机组虚拟惯量控制使得传动系统产生较为明显的扭振，将给相关零部件带来损害;另一反面，因为风电场有功出力中所包含振荡分量频率刚好在电力系统低频振荡频率区间(0.1～2.5 Hz)内，因此若低频振荡频率与传动系统扭振频率相近，则有可能引起低频振荡。

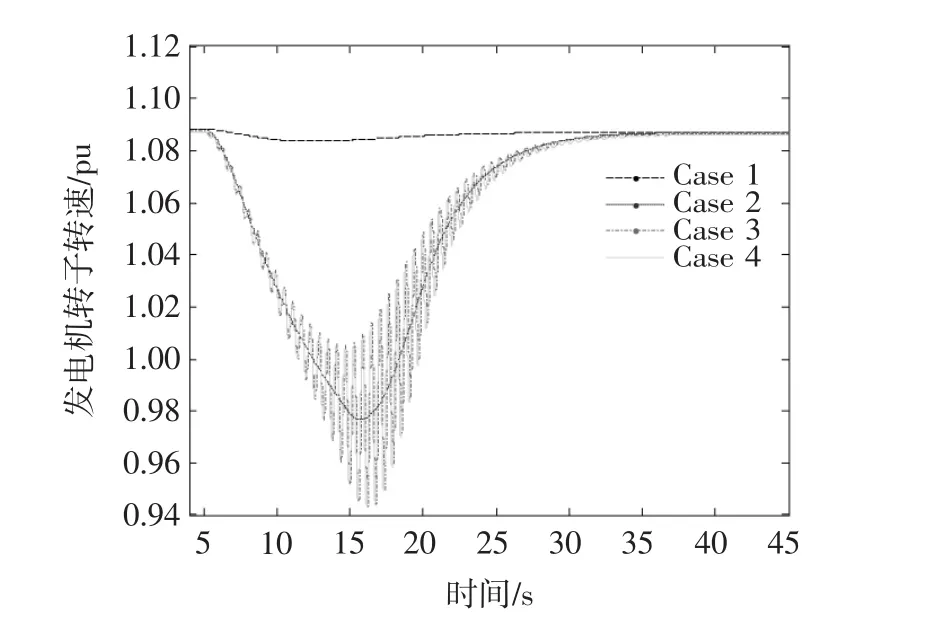
图8 双馈发电机转子转速变化曲线 (Case 1，2，3 and 4)Fig.8 Response of doubly fed induction generator rotor speed(Case 1，2，3 and 4)

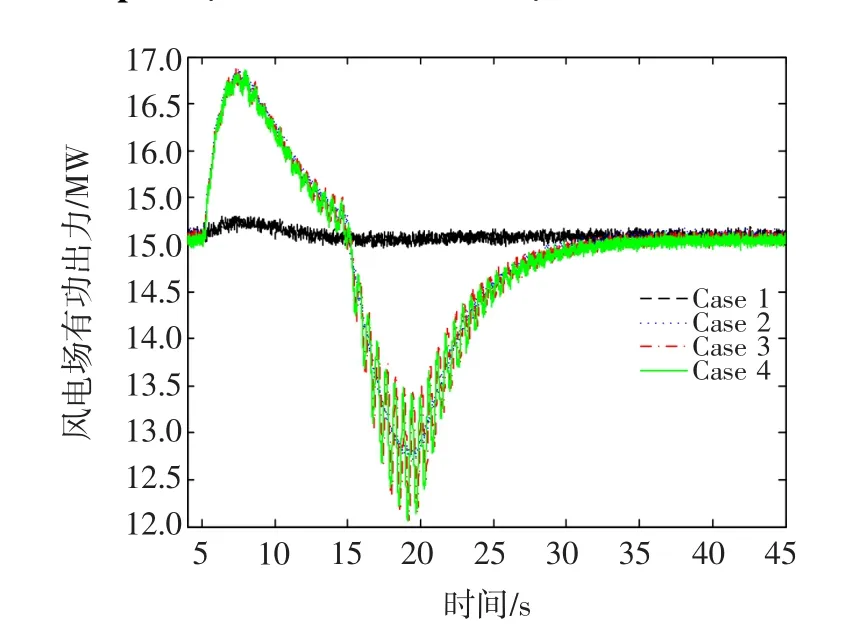
图9 风电场有功出力变化曲线 (Case 1，2，3 and 4)Fig.9 Response of active power of wind farm(Case 1，2，3 and 4)

综上，为了准确分析双馈风电机组对传动系统扭振的影响，必须采用2质块或3质块模型，而不能采用1质块模型。

4.3 扭振阻尼控制器有效性的仿真验证

在上述仿真系统的双馈风电机组的控制系统中加入上述扭振阻尼控制器。为了考察其效果，对下述情况进行仿真:

Case 5:双馈风电机组提供虚拟惯量控制，传动系统采用2质块模型，扭振阻尼控制器增益为Kdamp=0.25;

Case 6:双馈风电机组提供虚拟惯量控制，传动系统采用2质块模型，扭振阻尼控制器增益为Kdamp=0.50;

Case 7:双馈风电机组提供虚拟惯量控制，传动系统采用3质块模型，扭振阻尼控制器增益为Kdamp=0.25;

Case 8:双馈风电机组提供虚拟惯量控制，传动系统采用3质块模型，扭振阻尼控制器增益为Kdamp=0.50。

图10－图12分别给出了传动系统采用2块模型时(Case 3，5，and 6)系统频率、双馈发电机转子转速以及风电场有功出力的时域仿真波形。

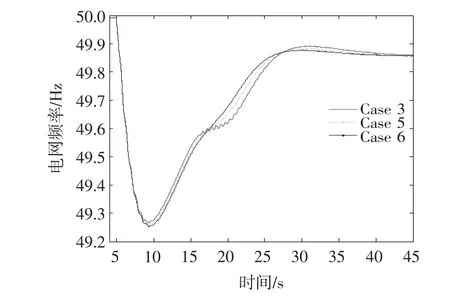
图10 电网频率变化曲线(Case 3，5 and 6)Fig.10 Response of grid frequency(Case 3，5 and 6)

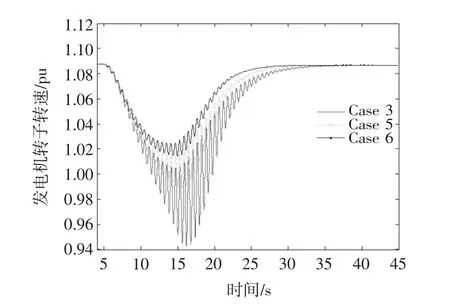
图11 双馈发电机转子转速变化曲线(Case 3，5 and 6)Fig.11 Response of doubly fed induction generator rotor speed(Case 3，5 and 6)

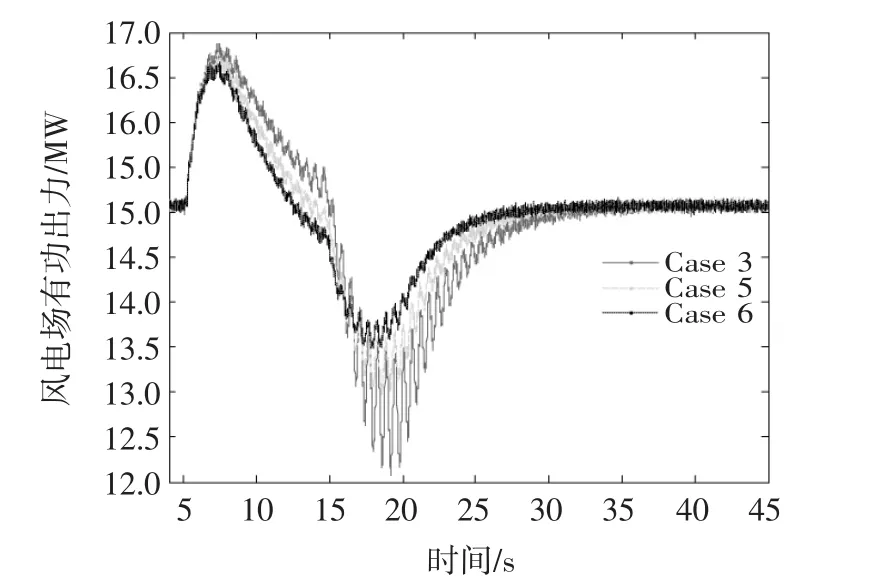
图12 风电场有功出力变化曲线(Case 3，5 and 6)Fig.12 Response of active power of wind farm(Case 3，5 and 6)

由图10可知，双馈风电机组加入扭振阻尼控制器之后，系统最低频率有所下降，并且控制器增益越大，最低频率下降的越多。由此可知，扭振阻尼控制器会在一定程度上减弱双馈风电机组虚拟惯量控制的效果。

由图11和图12可知，扭振阻尼控制器可以有效抑制转子转速和风电场有功出力的振荡，并且控制器增益越大，抑制的效果越好。由此可知，扭振阻尼控制器可以抑制扭振从而减少传动系统零部件的损耗，同时尽量减弱传动系统扭振与电力系统低频振荡之间的可能存在的相互作用。

图13～图15分别给出了传动系统采用3块模型时(Case 4，7，and 8)系统频率、双馈发电机转子转速以及风电场有功出力的时域仿真波形。传动系统采用3质块模型时，扭振阻尼控制器对双馈风电机组虚拟惯量控制的影响以及扭振抑制的效果与2质块模型基本一致，这里不再赘述。

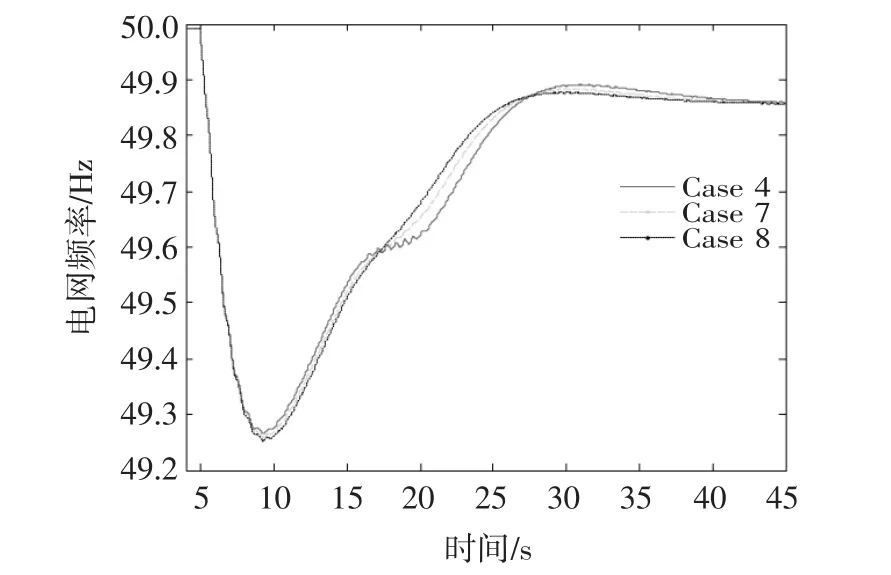
图13 电网频率变化曲线(Case 4，7 and 8)Fig.13 Response of grid frequency(Case 4，7 and 8)

综上，扭振阻尼控制器能够有效抑制风电机组虚拟惯量控制所引起的传动系统扭振，但会在一定程度上减弱双馈风电机组虚拟惯量控制的效果。

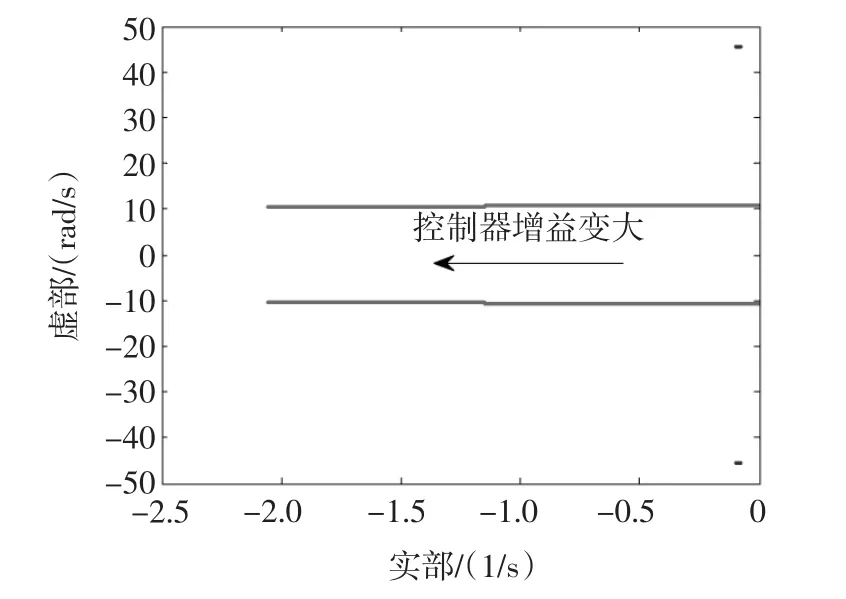
图16 随控制器增益变大，扭振模式的特征根轨迹Fig.16 Root loci of torsional mode with increasing controller gain

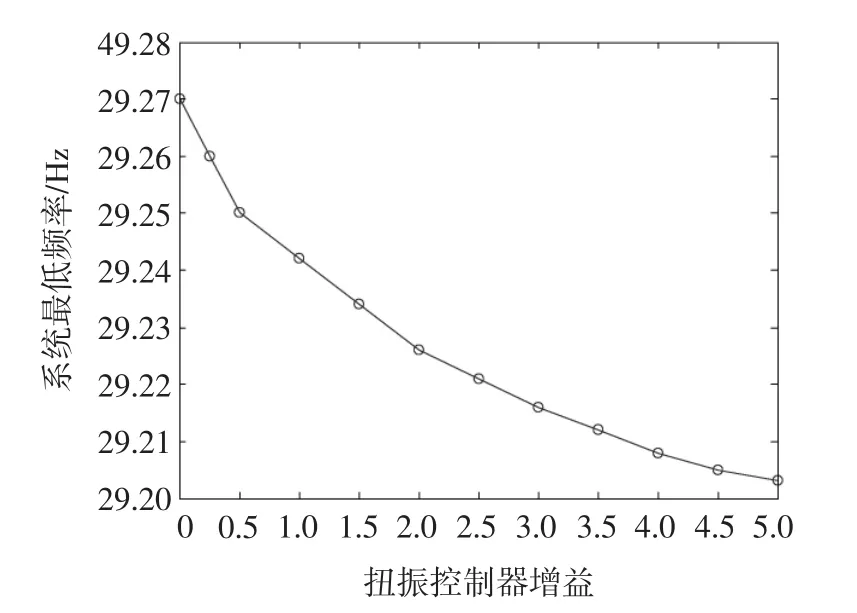
图18 随控制器增益变大，系统最低频率变化曲线Fig.18 Variations of grid frequency nadir with increasing controller gain

为了给扭振阻尼控制器的增益选取提供参考，图16、图17和图18分别给出了随着控制器增益的增大，传动系统(以3质块模型为例)的特征根轨迹、自然频率约为1.7 Hz的扭振模式的阻尼比，以及双馈风电机组虚拟惯量控制下电网最低频率的变化曲线。由图16、图17和图18可知，随着控制器增益增大，传动系统的特征根逐渐远离虚轴，其阻尼比逐渐增大，而系统频率最低值逐渐减小。因此，为了既不对虚拟惯量控制的效果造成太大影响，又能有效抑制传动系统扭振，必须选取适当的扭振阻尼控制器增益。

5 结论

本文基于不同的传动系统模型，分析了双馈风电机组虚拟惯量控制对传动系统扭振的影响。并设计了扭振阻尼控制器，以抑制虚拟惯量控制所引起的传动系统扭振。通过理论和仿真分析表明:

1)双馈风电机组传动系统1质块模型不能准确描述虚拟惯量控制对传动系统扭振的影响，而必须采用2质块或3质块模型;

2)对双馈风电机组虚拟惯量控制这一问题而言，传动系统分别采用2质块和3质块模型时的仿真结果基本一致，因此采用2质块模型以简化模型复杂度;

3)文中所设计的基于双馈发电机转子转速反馈的扭振阻尼控制器可以有效抑制扭振，但会在一定程度上减弱虚拟惯量控制效果。此外，随着扭振阻尼控制器增益的增大，虽然其对扭振抑制的效果越好，但同时对虚拟惯量控制的影响也越大。

以上结论有助于在设计双馈风电机组虚拟惯量控制时更加全面地考虑对自身传动系统以及对电力系统的影响。为此，我们下一步的工作将考虑如何更好地设计扭振阻尼控制器，既能有效抑制扭振，又能最大程度减小对虚拟惯量控制的影响。

［1］李俊峰，蔡丰波，乔黎明，等.中国风电发展报告［R］.北京:中国资源综合利用协会可再生能源专业委员会，2013.

［2］ERLICH I，RENSCH K，SHEWAREGA F.Impact of large wind power generation on frequency stability［C］//IEEE Power Engineering Society General Meeting，JUNE 18 －25，2006，Montreal，Que.NewYork:IEEE，2006:1 －8.

［3］DOHERTY R，MULLANE A，NOLAN G，et al.An assessment of the impact of wind generation on system frequency control［J］.IEEE Transactions on Power Systems，2010，25(1):452 －460.

［4］HOLDSWORTH L，EKANAYAKE J B，JENKINS N.Power system frequency response from fixed speed and doubly fed induction generator-based wind turbines［J］.Wind Energy，2004，7(1):21－35.

［5］EL MOKADEM M，COURTECUISSE V，SAUDEMONT C，et al.Fuzzy logic supervisor-based primary frequency control experiments of a variable-speed wind generator［J］.IEEE Transactions on Power Systems，2009，24(1):407 －417.

［6］EL MOKADEM M，COURTECUISSE V，SAUDEMONT C，et al.Experimental study of variable speed wind generator contribution to primary frequency control［J］.Renewable Energy，2009，34(3):833－844.

［7］CHANG Chien，LERen，LIN Weiting，et al.Enhancing frequency response control by DFIGs in the high wind penetrated power systems［J］.IEEE Transactions on Power Systems，2011，26(2):710－718.

［8］张昭遂，孙元章，李国杰，等.超速与变桨协调的双馈风电机组频率控制［J］.电力系统自动化，2011，35(17):20－25.ZHANG Zhaosui，SUN Yuanzhang，LI Guojie，et al.Frequency Regulation by doubly fed induction generator wind turbines based on coordinated overspeed control and pitch control［J］.Automation of Electric Power Systems，2011，35(17):20 －25.

［9］MAURICIO J M，MARANO A，GOMEZ-EXPOSITO A，et al.Frequency regulation contribution through variable-speed wind energy conversion systems［J］.IEEE Transactions on Power Systems，2009，24(1):173 －180.

［10］KAYIKCI M，MILANOVIC J V.Dynamic contribution of DFIG-based wind plants to system frequency disturbances［J］.IEEE Transactions on Power Systems，2009，24(2):859 －867.

［11］RAMTHARAN G，EKANAYAKE J.B，JENKINS N.Frequency support from doubly fed induction generator wind turbines［J］.IET Renewable Power Generation，2007，1(1):3－9.

［12］MORREN J，DE HAAN S W H，KLING W L，et al.Wind turbines emulating inertia and supporting primary frequency control［J］.IEEE Transactions on Power Systems，2006，21(1):433－434.

［13］MORREN J，PIERIK J，de HAAN SJOERD W H.Inertial response of variable speed wind turbines［J］.Electric Power Systems Research，2006，76(11):980－987.

［14］曹军，王虹富，邱家驹.变速恒频双馈风电机组频率控制策略［J］.电力系统自动化，2009，33(13):78－82.CAO Jun，WANG Hongfu，QIU Jiaju，Frequency control strategy of variable-speed constant-frequency doubly-fed induction generator wind turbines［J］.Automation of Electric Power Systems，2009，33(13):78－82.

［15］MUYEEN S M，ALI M H，TAKAHASHI R，et al.Comparative study on transient stability analysis of wind turbine generator system using different drive train models［J］.IET Renewable Power Generation，2007，1(2):131－141.

［16］RAMTHARAN G，JENKINS N，ANAYA L O，et al.Influence of rotor structural dynamics representations on the electrical transient performance of FSIG and DFIG wind turbines［J］.Wind Energy，2007，10(4):293－301.

［17］李辉，韩力，赵斌，等.风电机组等效模型对机组暂态稳定分析结果的影响［J］.中国电机工程学报，2008，28(17):105－111.LI Hui，HAN Li，ZHAO Bin，et al.Effect of equivalent models of wind turbines on analysis results of transient stability for wind generator systems［J］.Proceedings of the CSEE，2008，28(17):105－111.

［18］解大，王瑞琳，王西田，等.多机型风电机组机网扭振的模型与机理［J］.太阳能学报，2011，32(09):1281－1287.XIE Da，WANG Ruilin，WANG Xitian，et al.Models and principles of kinds of wind turbine for torsional vibration studies［J］.Acta Energiae Solaris Sinica，2011，32(09):1281－1287.

［19］郝正航，余贻鑫.励磁控制引起的双馈风电机组传动系统扭振机理［J］.电力系统自动化，2010，34(21):81－86.HAO Zhenghang，YU Yixin.Analysis on wind turbine driven dfig shaft torsional oscillation mechanism caused by excitation control［J］.Automation of Electric Power Systems，2010，34(21):81－86.

［20］张琛，李征，高强，等.双馈风电机组的不同控制策略对轴系振荡的阻尼作用［J］.中国电机工程学报，2013，33(27):135－144.ZHANG Chen，LI Zheng，GAO Qiang，et al.Damping effects on torsional oscillation of dfig drive-chain using different control strategies［J］.Proceedings of the CSEE，2013，33(27):135 －144.

［21］姚兴佳，王晓东，单光坤，等.双馈风电机组传动系统扭振抑制自抗扰控制［J］.电工技术学报，2012，27(1):136－141.YAO Xingjia， WANG Xiaodong， SHAN Guangkun， et al.Torque vibration active disturbance rejection control of double-fed wind turbine drive train［J］.Transactions of China Electrotechnical Society，2012，27(1):136 －141.

［22］LICARI J，UGALDE-LOO C E，EKANAYAKE J，et al.Comparison of the performance of two torsional vibration dampers considering model uncertainties and parameter variation［C］//European Wind Energy Association(EWEA)Annual Event，Copenhagen，Denmark，2012:16 －19.

［23］LICARI J，UGALDE-LOO C E，LIANG J，et al.Torsional damping considering both shaft and blade flexibilities［J］.Wind Engineering，2012，36(2):181 －196.

［24］李晶，宋家骅，王伟胜.大型变速恒频风力发电机组建模与仿真［J］.中国电机工程学报，2004，24(6):104－109.LI Jin，SONG Jiahua，WANG Weisheng，Modeling and dynamic simulation of variable speed wind turbine with large capacity［J］.Proceedings of the CSEE，2004，24(6):104－109.

［25］MULLER S，DEICKE M，DE DONCKER R W.Doubly fed induction generator systems for wind turbines［J］.IEEE Industry Applications Magazine，2002，8(3):26－33.

［26］TAPIA A，TAPIA G，OSTOLAZA J X，et al.Modeling and control of a wind turbine driven doubly fed induction generator［J］.IEEE Transactions on Energy Conversion，2003，18(2):194－204.