改进遗传蚁群算法及其在电机结构优化中的研究

谢颖， 李吉兴， 杨忠学， 张岩

(1.哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080;2.东北石油大学电气信息工程学院，黑龙江大庆163318)

0 引言

蚁群算法［1-3］是一种启发式仿生类并行的智能进化算法，它采用分布式并行计算和信息素正反馈机制，通过其内在的搜索机制，解决了一系列困难的组合优化问题，在旅行商问题、工件排序问题、背包问题、图着色问题、车辆调度问题和二次分配问题等离散型问题的领域上取得了有效的成绩。蚁群算法是意大利学者Marco Dorigo在1992年提出的［4］，比较完善地阐述了蚁群算法的原理［5］。Gutiahr W J首次对蚁群算法的收敛性进行了阐述，同时给出了一种改进蚁群算法，能够以一定概率收敛到最优值［6］。文献［7］中提出一种变异蚁群算法，有利地克服了基本蚁群算法中计算时间较长的缺陷。文献［8］采用一种动态自适应蚁群算法，能够有效地避免局部收敛，提高了算法的全局搜查能力。还有学者提出了免疫蚁群算法，能够解决约束关系的多任务调度问题［9］。遗传算法［10］是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法，其主要特点是群内搜索策略和群体中个体之间的信息交换、搜索不依赖于梯度信息。遗传算法是由美国 J.Holland教授提出的，他分析了群体方法搜索以及选择，交换等操作策略的重要性［11］。Cavicchio提出了以预选择策略保证群体多样性，对遗传算法参数进行中心控制［12］。Krishnakumar采用小群体方法，使得算法适应于动态系统的优化［13］。

蚁群算法是通过内部信息的积累和多次迭代更新而收敛于最优路径，因此具有全局的收敛能力，但是由于寻优开始阶段信息素不足，从而导致了寻优初期内部信息累积时间相对较长，求解相对缓慢。遗传算法具有良好的快速寻优能力，但是对于寻优过程中反馈回来的信息却没有加以使用，造成了大量没有意义的迭代，因此，遗传算法求取精确解的效率不高。二进制遗传蚁群算法确定了遗传算法与蚁群算法的融合时机，既充分地发挥了蚁群算法和遗传算法各自在寻优过程中的优点，又克服了遗传算法在搜索到一定程度时寻找最优解的效率不高以及蚁群算法在寻优开始阶段信息素不足的缺点，是求解效率和时间效率都比较好的智能算法。

本文采用的二进制遗传蚁群算法是将遗传算法和蚁群算法有效的结合起来。蚂蚁的位置和信息素的更新用二进制编码表示，能够使蚁群算法有效地处理连续变量问题，同时也能够更好地实现交叉、变异过程。将二进制遗传蚁群算法应用到电机的优化设计之中可使电机的性能得到较好的优化。

1 二进制遗传蚁群算法

1.1 优化过程

将蚁群的位置用二进制编码的变量组表示，变量组中可以有一个或多个变量，每一个变量用10位二进制数表示，二进制数的大小由变量的数值和取值范围决定。如数据的取值范围在a～b之间，则a由0000000000表示，b由1111111111表示，a～b之间的变量值y可以通过公式(1)由十位二进制数(b9b8b7b6b5b4b3b2b1b0)2转换

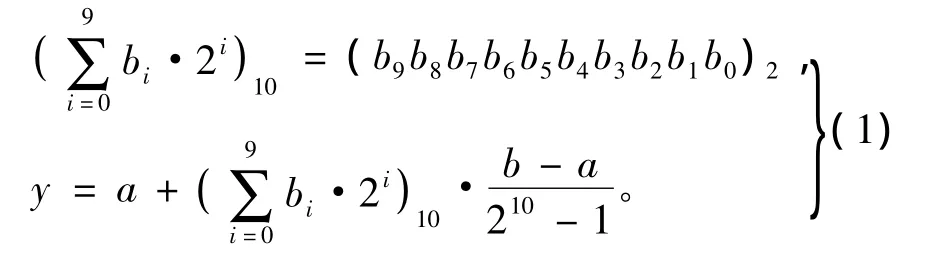
图1表示蚂蚁寻优的过程，如图所示，蚂蚁进行路径寻优时，从左边第一位开始，按照内在的搜索机制选择0状态还是1状态，转移概率表示为

式中:ak={0，1，…，n-1}表示蚂蚁k下一步允许选择的路径(t)表示信息素浓度因数(t)表示能见度因数;α表示信息素轨迹的相对重要性;β表示能见度的相对重要性。

从左到右按位选择0状态还是1状态，直到最后一位选择结束，进行信息素更新。

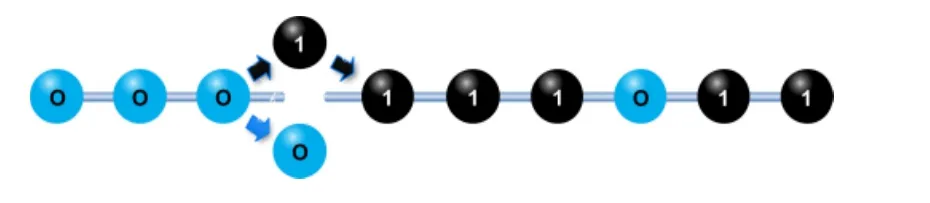
图1 二进制寻优Fig.1 Optimization map of binary

信息素更新之后，蚁群进行进化过程，即交叉、变异过程，如图2所示，此时，需要确定交叉概率pc和变异概率pm。图2(a)表示交叉过程，第一只蚂蚁信息链的前4位和第二只蚂蚁信息链的后3位进行重组，得到一组新的信息，图2(b)表示变异过程，蚂蚁信息链的某一位由状态0变为状态1，或由状态1变为状态0，寻优的结果为本次迭代的最优值，一次循环结束。

一次循环之后，蚁群进行下一轮循环，直到满足最大世代数。因此，二进制遗传蚁群算法如图3所示。

图2 二进制交叉变异寻优Fig.2 Optimization map of binary cross and mutation

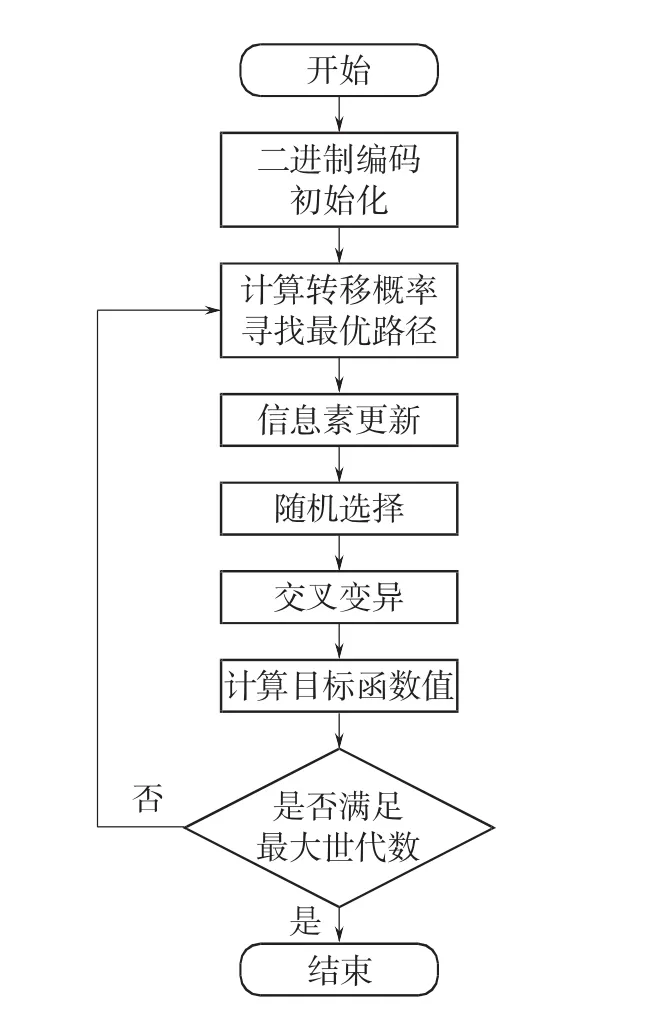
图3 二进制遗传蚁群算法寻优流程Fig.3 Optimization flow map of binary genetic ant colony algorithm

1.2 参数调节

蚁群在进行搜索时，需要确立一系列参数，其中主要包括α、β［14］。由于目前还没有有效的数学分析法确定每个情况下的最优参数，所以需要进行验证，图4为α、β取不同值时的收敛曲线，从图上可以看出，α、β取不同值时，收敛的结果不相同，当α=0.5、β =0.7 时，收敛值为最小，结果为最优。

1.3 函数验证

采用汇编语言实现了改进的二进制遗传蚁群算法，并且设置了有效的参数。为了验证该算法的性能，对表1中的三个函数进行优化仿真。

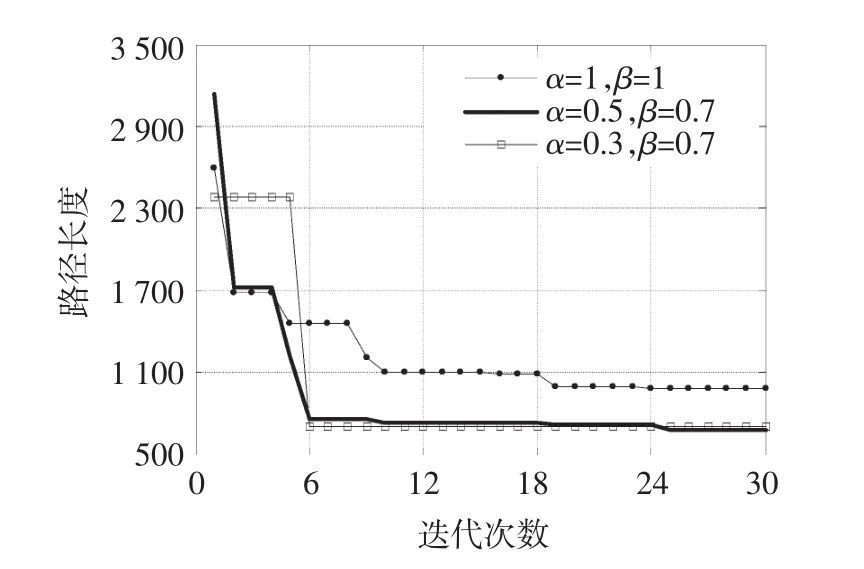
图4 α、β取不同值时的收敛曲线Fig.4 Convergence curves of different α and β

表1 优化函数Table 1 Optimizing functions

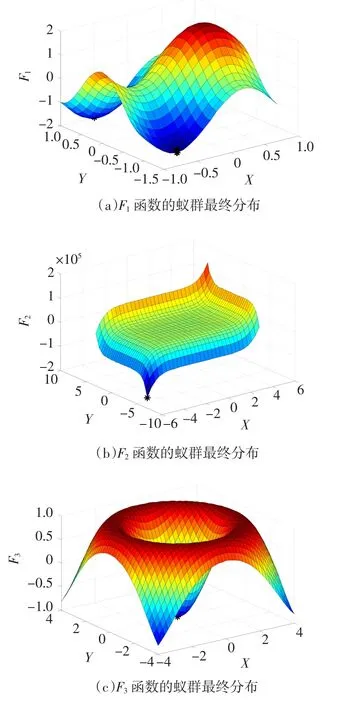
图5 蚁群最终位置分布Fig.5 Final position distribution of ants

图5表示蚁群的最终分布位置，从图中可以看出，蚁群最终分布在了3个函数的最小极值点上，由此可知，该算法具有良好的全局收敛能力。

图6 函数进化曲线对比Fig.6 Evolution curves of comparison map

图6 表示采用3种方法对函数优化的进化曲线，从图中可以看出，二进制遗传蚁群算法都在10次迭代左右收敛，且搜索到的值最小，由此可见，二进制遗传蚁群算法具有良好的全局搜索能力。

2 基于二进制遗传蚁群算法的优化设计

以一台4极7.5kW的自起动永磁同步电动机为研究对象，表2给出了电机的额定数据。采用改进的算法对电机的结构参数进行优化，通过优化电机的转子槽型宽度、铁心长度、每槽导体数、导线直径等结构参数，提高电机的性能。

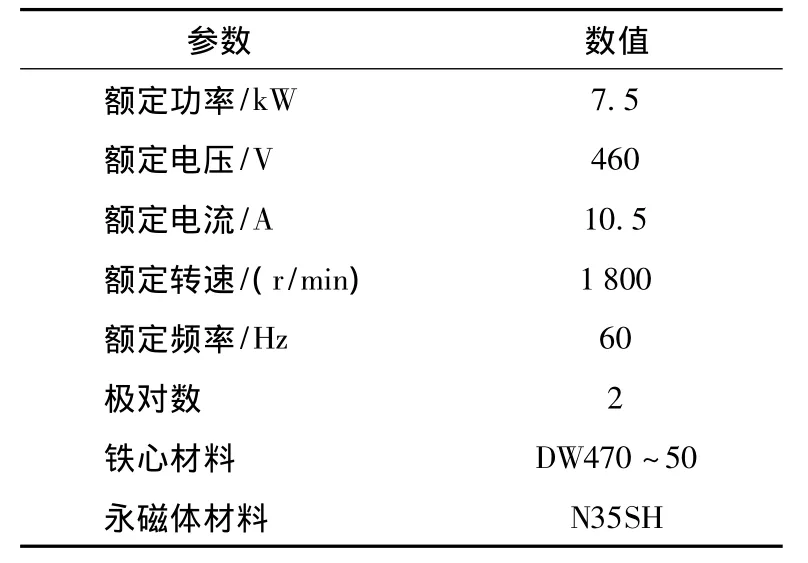
表2 异步起动永磁同步电动机的额定数据Table 2 Rated data of line-start permanent magnet synchronous motor

2.1 电机的基本结构

图7为电机的结构模型图，永磁体的形状和嵌放位置使得它在电机中的利用率很高，不需要单独建立隔磁桥。定、转子槽数之间的关系，使得电机有效的避免了同步附加转矩和单相震动力。

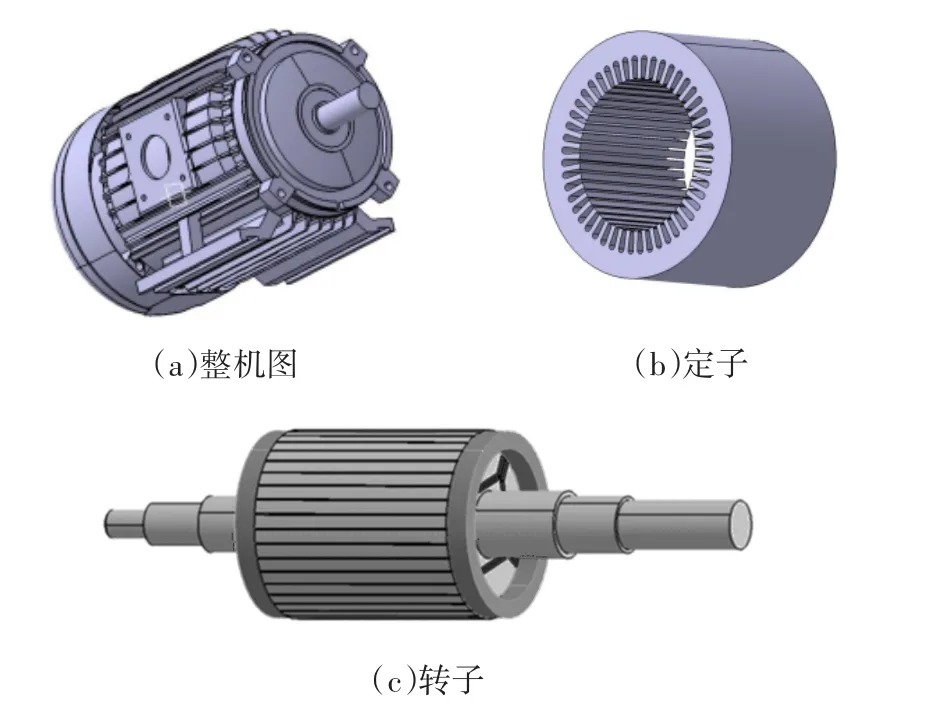
图7 电机结构模型Fig.7 Structure model of motor

2.2 优化设计的实现

改进的二进制遗传蚁群算法的基本数学模型可以表示为:

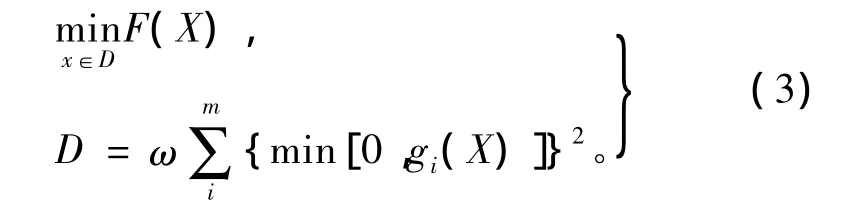
式中:F(X)为目标函数;X为结构参数;D为优化区间;ω为权重参数;m约束函数数量;gi是约束变量。

2.2.1 目标函数的选择

优化的目标包括效率、功率因数、起动转矩倍数、起动电流倍数和起动最小转矩倍数。在优化过程中，不是所有的性能都得到了较大的优化，只是以效率为主要的优化目标，其他的性能通过约束条件和惩罚函数来提高，使得它们优于原设计，主目标函数可以表示为

式中η为电机的效率。当效率为最大时，主目标函数的值是最小的，所以当算法搜索到定义区间内的最小值时，实现了电机的优化。

2.2.2 优化变量的选择

在选择优化变量时，需要选择对电机的性能影响较为明显的参数［15-17］，所以将每槽导体数、铁心长度、导线直径、转子槽型宽度设置为优化变量，通过在一定范围内改变这4个参数，从而找出函数的最小值，实现了蚁群寻优。

2.2.3 约束条件

异步起动永磁同步电动机的约束条件主要包括效率，功率因数，起动转矩倍数，起动电流倍数和起动最小转矩倍数［18-20］。它们可以表示为:

式中:η表示为电机的效率;cosφ表示为电机的功率因数;Tstmin表示为电机的起动最小转矩倍数;Ist表示为电机的起动电流倍数;Tst表示为电机的起动转矩倍数。

此外，设置槽满率在73% ～78%之间，定子齿、定子轭、转子齿、转子轭的磁密不超过1.8 T。电密不超过6 A/mm2，设置电磁计算的所有循环超过50次以后直接跳出，放弃当前运算，进入一轮寻优计算［21］，通过以上设置，可以保证电机的设计方案满足要求，能够有效地运行。

2.2.4 惩罚函数的设置

当得到的结果不满足约束条件时，需要设置相应的惩罚措施，从而保证算法能够快速、有效地找到最优极值点。利用约束条件，惩罚函数可以表示为:

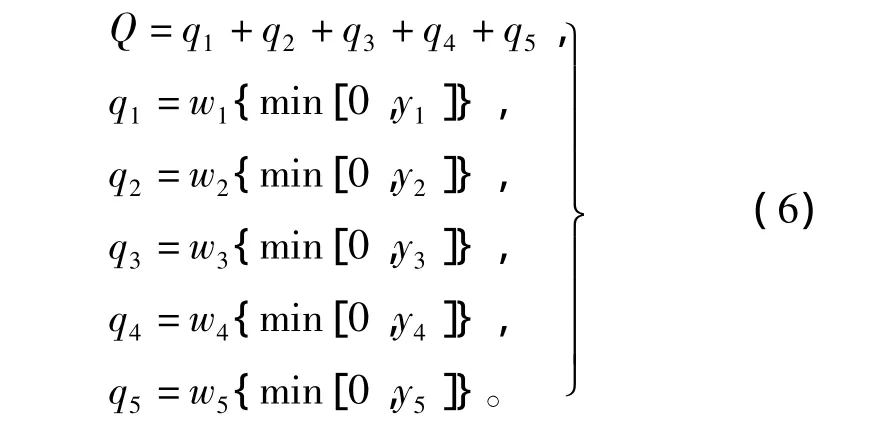
式中:w1、w2、w3、w4、w5为惩罚因子。

2.3 优化设计流程

文中建立了目标函数，设置了优化变量，限制了约束条件，给出了惩罚函数，根据已知条件，确立优化变量的变化范围。基于二进制遗传蚁群算法的电机优化设计流程如图8所示。

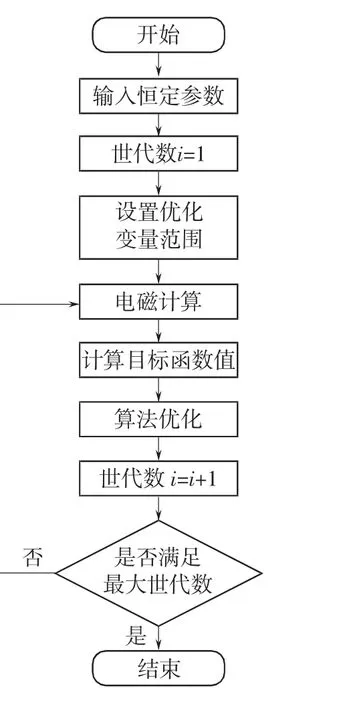
图8 电机优化流程Fig.8 Optimization flow map of motor

3 优化结果与分析

对一台7.5 kW的异步起动永磁同步电动机进行优化，以提高电机的效率作为主要目标，以每槽导体数、铁心长度、导线直径、转子槽型宽度作为优化变量，设置了约束条件和惩罚函数。图9表示电机物理模型。

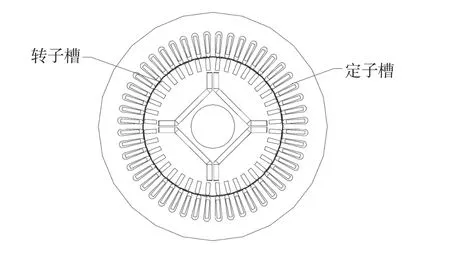
图9 电机物理模型Fig.9 Model of motor

3.1 优化结果

图10 表示蚁群寻找最优解的过程，20只蚂蚁随机分布在定义区间上，沿着圆柱母线方向的一组网格，表示一只蚂蚁的寻优过程。圆柱最下层的20个格表示20只蚂蚁第一次优化的结果，颜色表示目标函数的值，每一次循环结束，蚂蚁将沿着母线方向向上爬一个格，直到20次迭代结束。

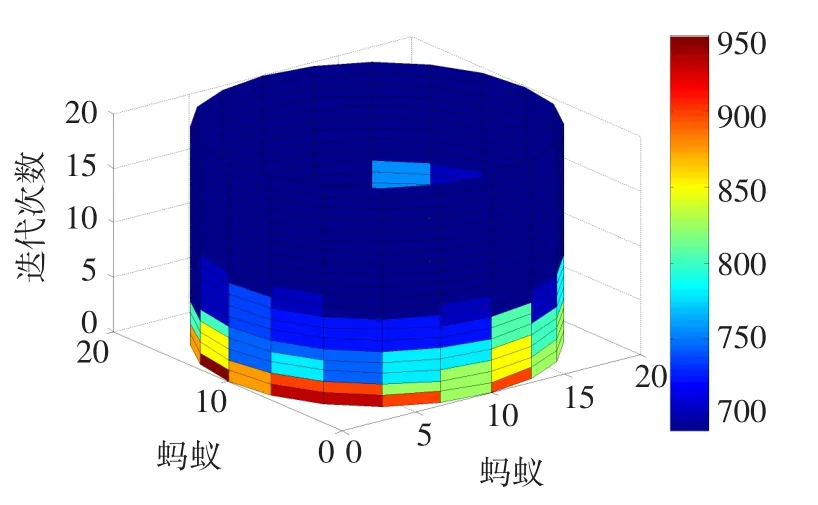
图10 蚁群寻优进化Fig.10 Evolution map of ants optimization

图11 表示二进制遗传蚁群算法的进化曲线，每一代的目标函数值表示为20只蚂蚁寻优值的平均值。从图中可以看出，蚁群最终找到了最优值。

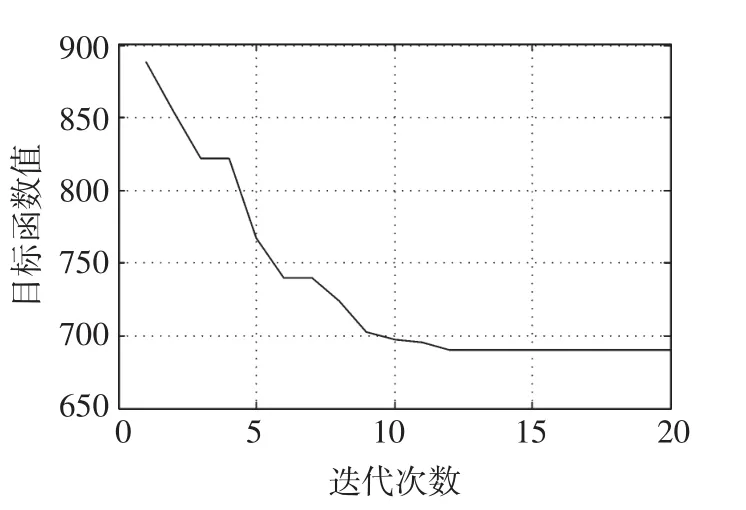
图11 进化曲线Fig.11 Evolution curve

表3给出了优化前后的性能比较，从表3中可以看出，和原设计相比，电机的效率、功率因数和起动转矩倍数都有所提高，电机性能得到了较好的优化。

表3 电机优化前后的参数对比表Table 3 Parameters comparison between original and optimized motor

3.2 有限元仿真

为了验证优化结果是否满足要求，利用AN-软件2D有限元对电机的起动性能和运行性能进行了分析，得到的结果分别如图12、图13和图14所示，图12为电机转矩和转速随着时间变化的曲线，图13为稳态时的磁密分布云图，图14为稳态时的电密的分布云图。

图12(a)表示转矩随着时间变化的曲线，图12(b)表示转速随着时间变化的曲线，其中虚线为原始曲线，实线为优化后的曲线。由图上可以看出，起动时优化后的转矩和转速曲线要比优化前的波动小，起动时间短，由此可知，电机的起动性能得到了较好的优化。

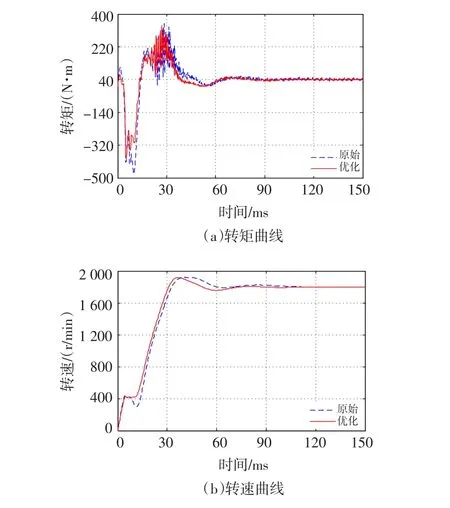
图12 电机的起动性能Fig.12 Starting performance of the motor

图13 表示电机在稳态时的磁密分布云图，图14表示电机在稳态时的电密分布云图。从图中可以看出，在稳态时齿部和额部的磁密以及绕组中的电密满足电机设计时的要求。

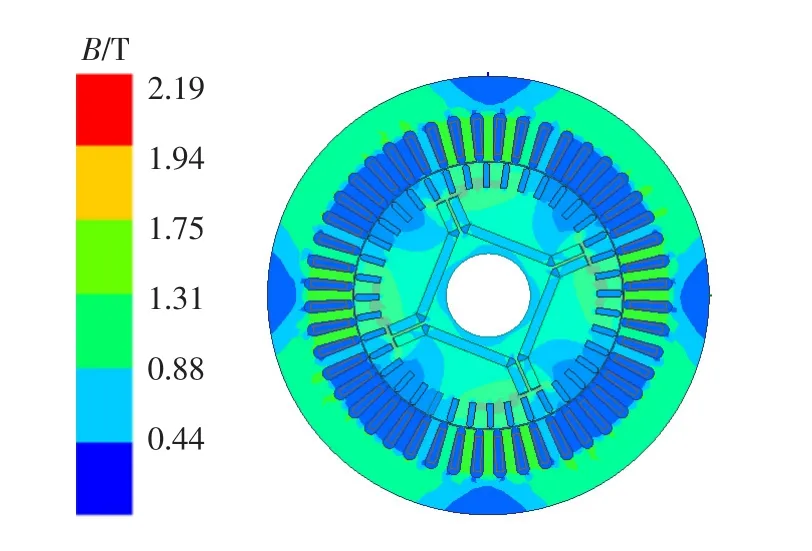
图13 磁密图Fig.13 Flux density map

图14 电密图Fig.14 Current density map

4 结论

本文介绍了一种二进制遗传蚁群算法，可以有效地解决连续变量的优化问题，并将其成功地引用到了自起动永磁同步电动机的优化设计之中。从进化曲线上可以看出，二进制遗传蚁群算法有很强的全局收敛能力和进化能力。通过采用二进制遗传蚁群算法对电机的结构参数进行优化，提高了电机的效率、电机的起动性能和运行性能，从而提高了电机的稳定性，增加了电机的寿命。因此，二进制遗传蚁群算法能使电机得到较好的优化，同时，也为其他电机优化设计提供了参考。

［1］M.DORIGO，M.BIRATTARI，T.STUTZLE.Ant colony optimization［J］.IEEE Computational Intelligence Magazine，2006，1(4):28-39.

［2］李士勇，陈永强，李妍.蚁群算法及其应用［M］.哈尔滨:哈尔滨工业大学出版社，2004.

［3］马良，朱刚，宁爱兵.蚁群优化算法［M］.北京:科学出版社，2010.

［4］COLOMAI A，DORIGO M，MANIEZZO V，et al.Distributed optimization by ant colonies［C］//Proceedings of the 1stEuropean Conference on Artificial Life，1991，134-142.

［5］DORIGO M，MANIEZZO V，COLOMA A.Ant system:optimization by a colony of cooperating agents［J］.IEEE Transaction on Systems，Man，and Cybernetics-Part B，1996，26(1):29-41.

［6］GUTJAHR W J.A graph-based ant system and its convergence［J］.Future Generation Computer System，2000，16(8):873-888.

［7］吴庆红，张纪会，徐心和.具有变异特征的蚁群算法［J］.计算机研究与发展.1999，36(10):1240-1245.WU Qinghong，ZHANG Jihui，XU Xinhe.An ant colony algorithm with mutation features［J］.Journal of Computer Research ＆

［8］李开荣，陈宏建.一种动态自适应蚁群算法［J］.计算机工程与应用，2004，29(2):152-155.LI Kairong，CHEN Hongjian.A dynamic and adaptive ant algorithm［J］.Computer Engineering and Applications，2004，29(2):152-155.

［9］钟一文，杨建刚.求解多任务调度问题的免疫蚁群算法［J］.模糊识别与人工智能，2006，19(1):73-78.ZHONG Yiwen，YANG Jiangang.Immune ant colony algorithm for multi-tast scheduling problem［J］.PR and AI，2006，19(1):73-78.

［10］陈国良，王煦法，庄镇泉.遗传算法及其应用［M］.北京:人民邮电出版社，2001.

［11］J.HOLLAND.Adaptation in natural and artificial systems［M］.In Yovits:Self-Organizing Systems，1962.

［12］J.CAVICCHIO.The Reproductive adaptive plans［C］//Proc.of the ACM 1972 Annual Conf，1972:1-11.

［13］KRISHNAKNMAR.Micro-genetic algorithm for stationary and non-Stationary function optimization［C］//SPIE Inteleigent Control and Adaptive Systems，1989:289-296.

［14］CHEN Zhenfeng，ZHONG Yanru，LI Jie.Parameter identification induction motor using ant colony optimization［C］//Proc.of Int.Conf.on Evolutionary Computation(CEC 2008)，2008:1611-1616.

［15］LIU Wenbiao，CAO Yangjie，ZHANG Yuan，et al.Parameters optimization of synchronous induction coilgun based on ant colony algorithm［J］.IEEE Transactions on Plasma，2011，39(1):100-104.

［16］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，1997:193-233.

［17］王秀和，杨玉波，朱常青.异步起动永磁同步电动机理论设计与分析［M］.北京:机械工业出版社，2009:115-141.

［18］ZHAO Baojiang，LI Shiyong.Ant colony optimization algorithm and its application to neuro-fuzzy controller design［J］.BIAI Transactions on Systems Engineering and Electronics，2007，18(3):603-610.

［19］于力.基于遗传算法的中小型同步电机优化设计［D］.长沙:湖南大学，2007.

［20］孟大伟，吕海鹏，徐磊.自适应蚁群算法在YKK系列中型高压电机优化设计中的应用［J］.大电机技术，2010:1-4.MENG Dawei，LÜ Haipeng，XU Lei.Adaptive ant colony algorithm used in optimization of medium high voltage motor of kky series［J］.Large Electric Machine and Hydraulic Turbine，2010:1-4.

［21］杨勇，宋晓峰，王建飞，等.蚁群算法求解连续空间优化问题［J］.控制与决策.2003，18(5):573-576.YANG Yong，SONG Xiaofeng，WANG Jianfei，et al.Ant colony algorithm for continuous space optimization［J］.Control and Decisions，2003，18(5):573-576.