基于首次穿越破坏的TMD 体系频域可靠性分析

谭 平， 刘良坤， 李祥秀， 张 颖， 周福霖，

(1. 广州大学工程抗震研究中心，广东 广州510405;2. 北京工业大学建筑工程学院，北京100124)

可靠度分析在工程结构中的应用较为广泛.结构受静力作用时的可靠度容易求得，即使受到随机地震激励，在一般情况下，其动力可靠度也可根据首次穿越破坏理论［1-2］近似求解. 结构在随机激励下的可靠度分析一直是个难点，较为精确的计算可采用Monte Carlo 方法，但相比其计算量是得不偿失的.为此，文献［3］基于首次穿越破坏的Possion极值破坏理论，建立了随机结构动力可靠度功能函数，并采用与响应面法结合的验算点法对结构的失效概率进行了计算，但是每次计算需要进行迭代求解验算，过程比较繁琐. 文献［4］基于随机有限元摄动法计算了结构在非平稳激励下的结构动力可靠度.文献［5］采用摄动法结合Edgeworth 级数技术，分析了任意分布参数的梁结构刚度可靠性灵敏度问题.文献［6-7］通过Hermite 多项式逼近［8］与降维法［9］，将多维动力可靠度问题转换成一维问题，具有较高的精度与效率.文献［10-13］基于概率密度演化方法求解结构复合随机振动等情况的可靠度，该方法不需期望穿越阈值等假定，且具有较高精度，给出了结构的概率信息演化过程新形式，并对非线性情况作了一定阐述.

外激励频率对结构响应的影响是不可忽略的，那么结构的可靠度也必然与外激励频率相关.尽管在单随机、复合随机、灵敏度等方面的可靠度计算有较大改善，但尚未出现关于频率的可靠度分析，本文提出频域可靠度的概念，并采用对频率敏感性强的调谐质量阻尼器(tuned mass damper，TMD)结构体系作为算例，进行随机地震激励下的可靠度分析.

1 结构的随机地震响应分析

结构的随机地震响应计算方法除传统方法外，还可利用虚拟激励法［14］求解. 假设结构在地震作用下的运动方程为

式中:

M、C、K 分别为结构的质量、阻尼、刚度矩阵;

I 为单位列向量;

¨ug为地面运动加速度.

式(1)中假设地震动为平稳随机激励，且为Kanai-Tajimi 谱模型，则响应自谱为

式中:

S 为结构响应谱密度;

ω 为外激励频率;

H(ω)为传递函数;

Sug为地震动谱密度.

由以上分析，可求出结构地震激励响应的i 阶谱矩

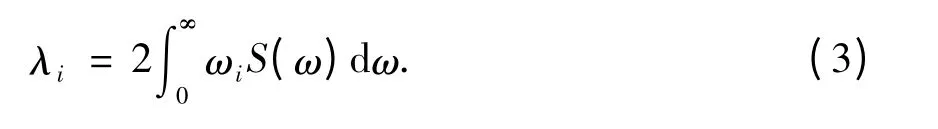
2 首次穿越破坏

结构受到地震作用，其动力可靠度可近似采用首次穿越破坏计算. 当响应限值较大时，出现交叉的概率较低，此时可认为结构动力响应与允许界限的交叉服从Poisson 分布.但Poisson 分布假定对宽带过程和低阈值水平的计算结果可能不安全，而对窄带过程又偏于保守. 此时可用Vanmarcke 基于Markov 过程假定［1-2］的改进概率计算公式:

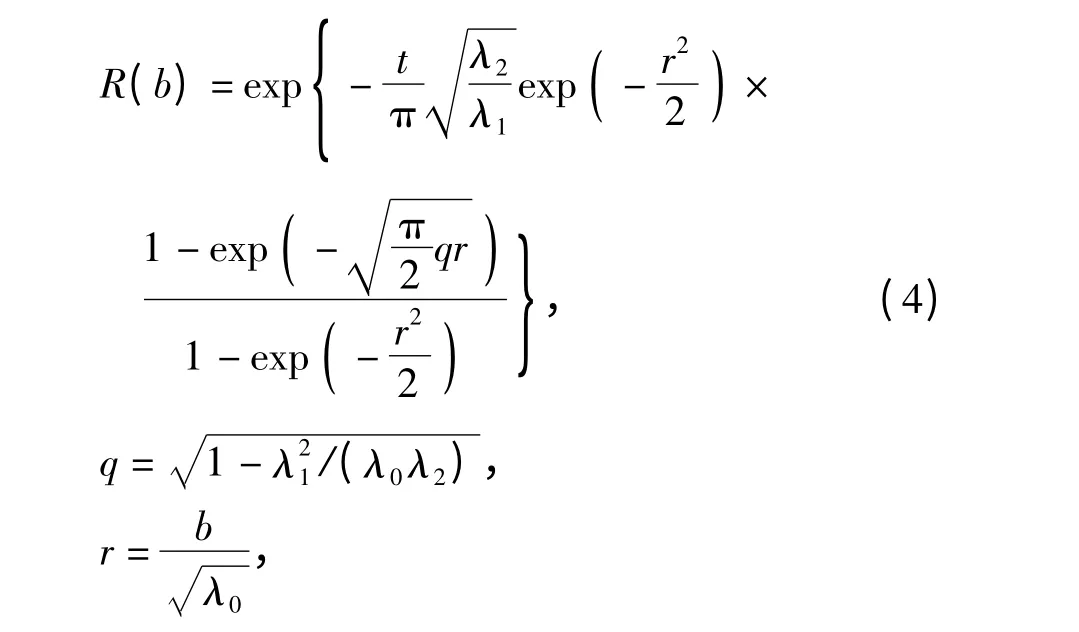
式中:

b 为界限值;

t 为地震激励时间.

一般来说，工程结构可简化为串联体系，其串联后的可靠度按下式计算:

式中:

Pi为各楼层、减震装置等各串联部分的可靠度.

式(5)表示任意结构的破坏都将直接与总可靠度P 直接相关.

3 动力可靠度的频域概率分布

由于Poisson 分布对宽带过程误差较大，窄带过程又偏于保守，本文将利用Vanmarcke 基于Markov 过程假定的修正式(4)来分析概率分布.显然，由式(4)可知结构的动力可靠度与所选取的激励时间t、激励谱密度Sug有关，但实际结构的可靠性也受激励频率的影响，因为激励频率接近结构振动频率时更易使其失效.通过式(3)也发现谱矩的计算是激励频率的无穷积分的结果，这也说明了可靠度是与激励频率相关的.可以将谱矩的无穷上限用变量ωt代替(ωt称为截止频率).若假设随机地震激励为高斯平稳过程，此时将式(3)中的谱矩积分表达改写成如下形式:

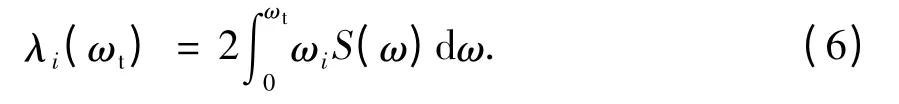
式(6)物理意义为:当取某截止频率ωt后结构响应关于截止频率的谱矩. 由此，式(4)的谱矩及其关联项可用式(6)计算，当地震激励时间和激励谱强度确定时，代入式(4)计算出的动力可靠度就是关于截止频率ωt的函数:

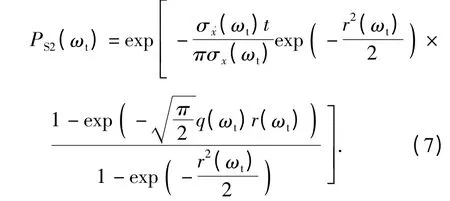
式(7)的物理意义为:当取某截止频率ωt后，结构响应关于截止频率的动力可靠度. 因此，只要通过改变截止频率ωt即可求得结构的动力可靠度关于频率分布的情况. 此时，尽管可以求得结构动力可靠度关于频率的分布，但还没有给出关于频率的概率密度分布.求频率概率密度的解析解相对困难，但可转变思路，先用式(7)求得关于截止频率的动力可靠度，再用向前差分方法即可求出关于频率的概率密度.向前差分具有一阶精度，当ωt的变化量较小时，求出的结构动力可靠度关于频率的概率密度信息的精度可满足分析要求.利用向前差分计算概率密度，可求得结构动力可靠度关于频率的概率密度如下:

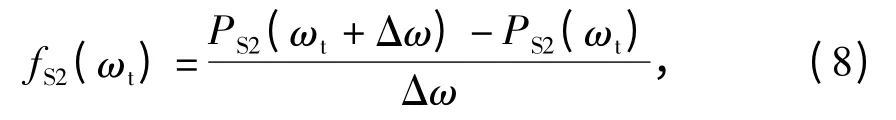
式中:

Δω 为频率增量.

求得结构动力可靠度关于频率的概率密度信息fS2(ωt)后，再用式(5)可求得整体结构的总概率信息.值得注意的是，由于积分的上限值ωt为变量，随着上限值的增大可靠度下降，当ωt→∞时，结果与式(4)计算的可靠度相同，此时包含所有频率成分，其可靠度显然最低.

根据前述分析，随着积分上限值的增大可靠度下降，因而可靠度关于截止频率ωt的导数是负数，即关于频率的概率密度值也就是负数，这也就是说基于频率的可靠度随频带带宽的增大逐渐变小，趋于式(4)首次穿越破坏可靠度;若从随机响应来看，随着频率积分上限的增加，随机响应数值增大，那么超越界限的概率加大，将导致结构易失效，即其可靠度会下降.这也就解释了关于频率的概率密度是负数的原因.若求某个频段的概率减少量可将式(8)进行积分或用式(7)作减法运算，即

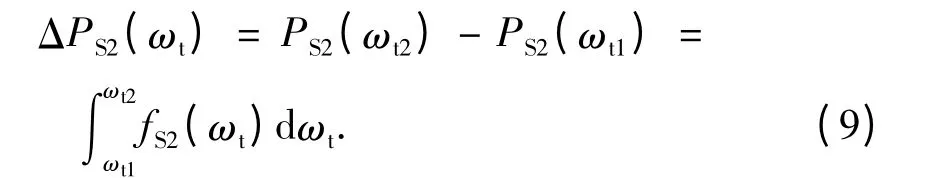
需要注意的是，在分析频域概率过程中，当激励时间确定、激励较小时，可靠度一直接近1，此时基于频率的分析将不明显，反映不出结构关于频率的动力可靠度信息.可增大激励强度以凸显出某些频率对结构可靠度的影响，以便进行结构可靠度分析.

4 TMD 结构体系动力频域可靠度分析

由于TMD 结构体系对频率较为敏感，本节将其作为算例研究基于频域的动力可靠度问题.假设某10 层钢框架结构基本周期为1.085 s，层质量为20 000 kg，层 剪 切 刚 度 为 30 MN/m，层 高为2.55 m，结构阻尼矩阵采用瑞雷阻尼，并假定结构阻尼比为0. 02;地震动谱密度模型为Kanai-Tajimi 谱模型，按文献［15］取二类场地，为使频域概率信息表达更清晰，取8 度远场小震，地震动时间20 s，并假设其层间位移限值按规范取为层高的1/300，即为0.012 m.若TMD 的质量比为0.01，其频率比与阻尼比均按Den Hartog 公式［16］设计.

假设本算例为串联结构体系，求得频域累积概率和概率密度分布如图1 和图2 所示.

图1 为结构总频域概率随频率的分布情况(此处频率为圆频率，下同)，图2 为结构总频域概率密度随频率的分布情况. 随着频率的变化，无控制结构的最终可靠度趋于0.246 2，TMD 结构体系的最终可靠度趋于0.969 6.因此，从频域累积概率图1 上看，TMD 可提高结构的可靠性.

图1 与第3 节所述一致，即随着积分上限的增大，结构可靠度降低.这是因为随着频带加宽，结构响应方差也在加大，最终导致了结构可靠性的降低.

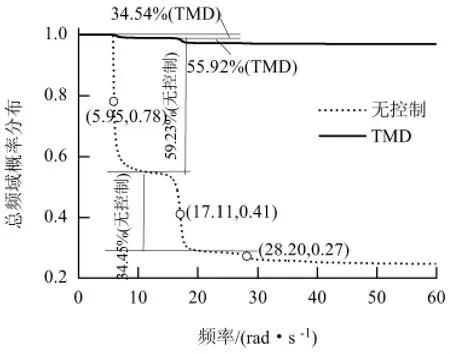
图1 频域累积概率分布Fig.1 Distribution of cumulative probability in frequency domain

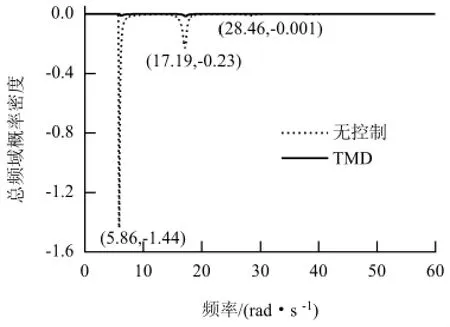
图2 频域概率密度Fig.2 Probability density in frequency domain

从图1 中可发现，无控结构的概率出现了3 个较为明显的下降段.在图1 中大致绘出其概率分布曲线下降段的中心点(横向箭头处)，这些中心点依 次 对 应 的 外 激 励 频 率 分 别 为5. 95、17. 11、28.20 rad/s，而实际结构的前3 阶频率为5. 79、17.24、28.30 rad/s. 那么从频域可靠性的角度看，结构动力可靠度下降的原因可归结为在此频率处，外激频率刚好与结构频率接近导致共振发生，其响应增大，即降低了可靠度，这就是出现3 个明显下降段的原因.实际上还有其他不明显的下降段，这些下降段受这些高阶振型的影响较小.从图2 中也发现概率密度负值绝对值最大处(谷点)对应的外激励频率为5.86、17.19 和28.46 rad/s，其原因与前述分析类似.

图1 与图2 中的表明，TMD 可提高结构的可靠性.在图1 中一阶频率对应的拐点附近，TMD 结构体系的可靠度下降量很小;从图2 的概率密度幅值也可得知，当结构无控时在一阶频率处的可靠度下降量却很大，这表明TMD 主要控制结构的一阶响应.另外，图2 中无控结构一阶频率对应的TMD结构体系的频率概率密度为-0.011 78，二阶频率对应的为- 0. 156 60，这表明与无控结构相比，TMD 结构体系的频率概率密度在二阶频率处的下降幅度比一阶频率处快.

无控结构在前两阶频率附近可靠度下降量(1 阶频率对应可靠度与其他各阶频率对应可靠度之差)，以及可靠度总下降量(1 阶频率对应可靠度与最终可靠度之差)的比值如图1 所示.结构无控时前两阶下降比例为59.23%和35.45%，此时对应的TMD 结构体系则为34.54%和55.92%，这表明TMD 结构体系在一阶频率处的可靠度下降比例小，主要控制一阶振型.此外，这也表明对于无控结构，其可靠度对频率的敏感性随振型阶数的提高是降低的，而TMD 结构体系则在无控结构对应的二阶频率出敏感性最强，一阶频率处敏感性稍弱，其它阶则不明显.

若分析结构各楼层的频域概率累积分布与频域概率密度分布，可发现其基本结论与上述的总频域概率信息是一致的. 图3(a)为无控时各楼层频域概率随频率的分布情况，图3(b)为无控时各楼层域概率密度随频率的分布情况.

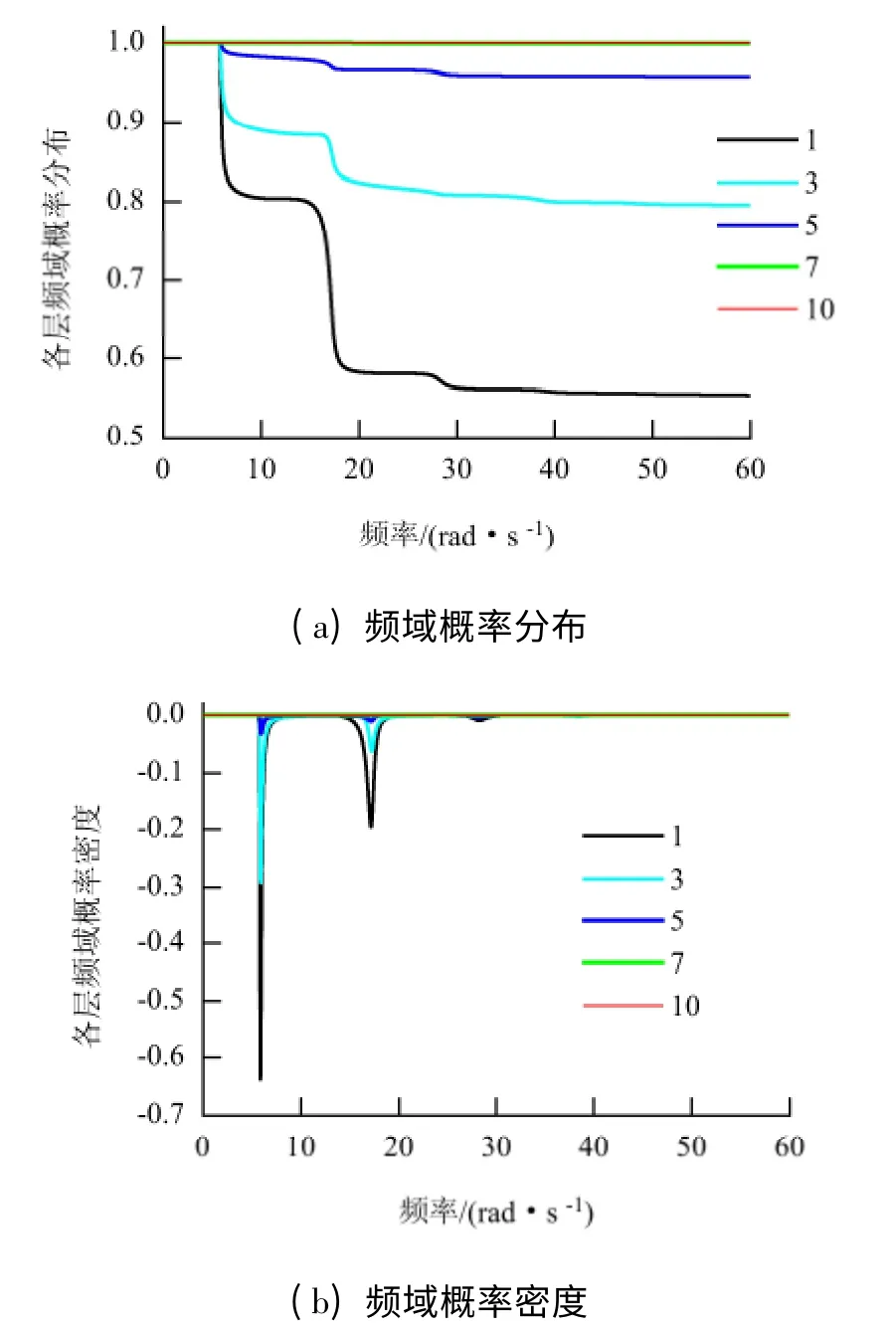
图3 无控结构频域概率分布与概率密度Fig.3 Distribution of cumulative probability and probability density in frequency domain without control

图4 是相应的频域概率信息在TMD 控制时的情况.

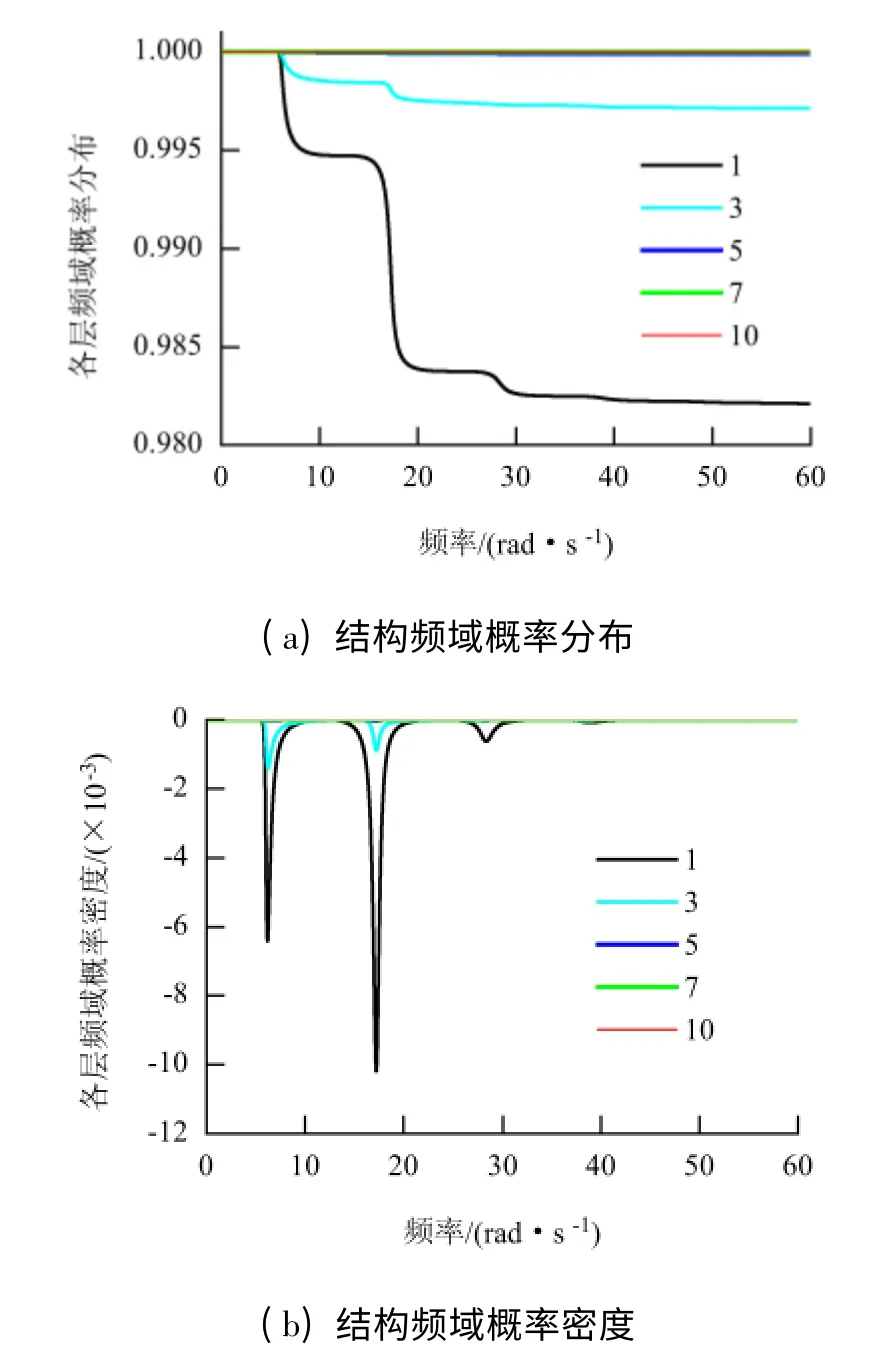
图4 TMD 结构频域概率分布与概率密度Fig.4 Distribution of cumulative probability and probability density in frequency domain for TMD

从图3 与图4(图中1、3、5、7、10 表示选取的代表楼层)可见，TMD 结构体系对下部结构可靠度的影响较大.图4 结果表明第1 层的频域可靠度与图2 中结构整体可靠度一致，但第3 层TMD 结构体系在一阶频率处的影响更大，总体上二阶频率处结构可靠度的下降较多.这也从可靠度概率分布的角度说明了TMD 主要控制结构的一阶频率响应，在其他振型可能有放大作用. 其他楼层的概率信息分析过程类似，在此不再赘述.

5 结束语

通过提出频域可靠度的概念，利用首次穿越破坏准则，给出了结构在随机激励下关于频域的概率分布计算公式，并采用向前差分方法求出关于频率的概率密度，用本文方法分析了TMD 结构的频域概率信息，得出以下结论:

(1)频域可靠度是可靠度关于谱矩截止频率的概率特征，其关于截止频率的概率密度为负数.

(2)频域可靠度分析频率敏感性结构具有优势，例如可以解释TMD 结构体系的减震可靠性.

(3)频域可靠度分析可以从激励频率角度解释结构可靠度性损失情况，从而获得结构在各阶外激励频率下的可靠度，为合理改善结构频率特性提供了依据.

因此，频域可靠度分析对频率敏感结构的设计具有借鉴意义，采用本文的分析方法可以反映频率特性对结构动力可靠度的影响.

［1］ 朱位秋. 随机振动［M］. 北京:人民交通出版社，1990:474-502.

［2］ 李桂青，李秋胜. 工程结构时变可靠度理论及其应用［M］. 北京:科学出版社，2001:152-170:

［3］ 陈颖，王东升，朱长春. 随机结构在随机荷载下的动力可靠度分析［J］. 工程力学，2006，23(10):82-85.CHEN Ying，WANG Dongsheng，ZHU Changchun.Dynamic reliability analysis of stochastic structures subjected to random loads［J］. Engineering Mechanics，2006，23(10):82-85.

［4］ CHAUDHURI A，CHAKRABORT S. Reliability of linear structure with parameter uncertainty under nonstationary earthquake［J］. Structure Safety，2005，28:231-246.

［5］ 张义民，贺向东，刘巧伶，等. 任意分布参数的梁结构刚度可靠性灵敏度分析［J］. 计算力学学报，2007，24(6):785-789.ZHANG Yimin，HE Xiangdong，LIU Qiaoling，et al.Stiffness reliability-based sensitivity analysis of beam structure with arbitrary distribution parameters［J］.Chinese Journal of Computational Mechanics，2007，24(6):785-789.

［6］ 乔红威，吕震宙，关爱锐，等. 平稳随机激励下结构动力可靠度分析的多项式逼近法［J］. 工程力学，2009，26(2):60-64.QIAO Hongwei，LÜ Zhenzhou，GUAN Airui，et al.Dynamic reliability analysis of stochastic structures under stationary excitation using Hermite polynomials approximation［J］. Engineering Mechanics， 2009，26(2):60-64.

［7］ 乔红威，吕震宙. 平稳随机激励下随机结构动力可靠性分析［C］∥2007 年第九届全国振动理论及应用学术会议. 杭州:［s. n.］，2007:57-62.

［8］ BAROTH J，BODE L，BRESSOLETTE P，et al. SFE method using Hermite polynomials:an approach for solving nonlinear mechanical problems with uncertain parameters［J］. Computer Methods in Applied Mechanics and Engineering，2006，195(44):6479-6501.

［9］ RAHMAN S，XU H. A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics［J］. Probabilistic Engineering Mechanics，2004，19(4):393-408.

［10］ 陈建兵，李杰. 复合随机振动系统的动力可靠度分析［J］. 工程力学，2005，22(3):52-57.CHEN Jianbing， LI Jie. Dynamic reliability assessment of double random vibration systems［J］.Engineering Mechanics，2005，22(3):52-57.

［11］ 李杰，陈建兵. 随机结构动力反应分析的概率密度演化方法［J］. 力学学报，2003，35(4):437-442.LI Jie，CHEN Jianbing. Probability density evolution method for analysis of structure dynamic response［J］.Acta Mechanica Sinica，2003，35(4):437-442.

［12］ 陈建兵，李杰. 非线性随机结构动力可靠度的密度演化方法［J］. 力学学报，2004，36(2):196-201.CHEN Jianbing，LI Jie. The probability density evolution method for dynamic reliability assessment of nonlinear stochastic structure［J］. Acta Mechanica Sinica，2004，36(2):196-201.

［13］ 彭勇波，李杰. 非线性随机振动分析的概率密度演化方法［J］. 西南交通大学学报，2014，49(2):220-226.PENG Yongbo，LI Jie. Probability density evolution method of nonlinear random vibration analysis［J］.Journal of Southwest Jiaotong University， 2014，49(2):220-226.

［14］ 林家浩，张亚辉. 随机振动的虚拟激励法［M］. 北京:科学出版社，2004:42-54.

［15］ 张治勇，孙柏涛，宋天舒. 新抗震规范地震动功率谱模型参数的研究［J］. 世界地震工程，2000，16(3):33-38.ZHANG Zhiyong，SUN Baitao，SONG Tianshu. Study on the parameters of seismic power spectrum model based on the new seismic code［J］. World Information on Earthquake Engineering，2000，16(3):33-38.

［16］ DEN HARTOG J P. Mechanical vibrations［M］. 4th ed. New York:McGraw Hill，1956:51-55.