基于容腔调节的钢轨打磨压力控制系统

聂 蒙， 李建勇， 沈海阔

(北京交通大学机械与电子控制工程学院，北京100044)

早期的打磨列车在打磨压力输出方面大多采用液压传动的方式［1］. 气动技术本身具有低成本、无污染以及高安全性等优势，在钢轨打磨方面有着逐渐取代液压传动系统的趋势［2］. 在打磨作业过程中，由于车体晃动以及钢轨自身不平顺等原因，给压力控制系统带来强制扰动，导致打磨压力波动，最终影响打磨质量甚至造成钢轨损伤［3］. 而气动系统固有的强非线性导致了控制打磨压力波动的难度增大.研究钢轨打磨过程中如何降低气动系统压力波动，对于设计钢轨打磨列车以及提高钢轨打磨质量有着重要的意义［4］.

学者们从改变气动系统结构、提升气动元件精度以及研究控制算法等方面开展研究，以获得更高的压力控制精度.文献［5］在气动位置伺服控制系统中引入压力反馈，构建压力观测器以加快系统响应速度.文献［6］为气缸设计了滑模压力控制器，通过设定较高的反馈系数来提高系统鲁棒性. 文献［7］利用PWM(pulse width modulation)脉冲控制启动开关电磁阀来构建压力控制系统.文献［8］在电气比例压力阀控制系统中采用三阶CARMA 模型描述实际系统，获得较好的压力响应特性. 文献［9］用最小二乘法对压力系统参数进行辨识，降低了系统超调量.

上述文献都是在假定额定力负载的情况下进行压力控制研究，对于强制扰动作用下的系统稳定控制研究较少.本文针对钢轨打磨作业环境中，气动压力控制系统的强非线性、多控制对象以及扰动受迫性等特征，提出一种基于容腔调节的气动压力控制系统.通过分析该系统工作原理，结合作业环境建立其数学模型，研究了相应的控制策略，最终实现在保障打磨压力控制精度的前提下，降低强制扰动作用带来的压力波动问题.

1 容腔调节器模型

由于气动系统的能量传输介质是空气，具有弹性模量小、可压缩性大的特点，系统工作特性与系统 的容腔体积有较大关系［10］.研究表明［11］，提高气缸无杆腔大小能够有效降低外部扰动带来的压力波动.因此，在压力控制系统中加入容腔调节装置将对提高系统抗扰动能力起到较大作用.

容腔调节器的主要作用是通过间接调节系统容腔大小来提高系统抗扰动的能力. 打磨过程中，当扰动较大时，通过增大打磨气缸施压端容腔吸收压力波动，在平稳阶段减小，打磨气缸施压端容腔提高系统响应速度.

1.1 容腔调节器结构

图1 所示为容腔调节器的结构原理图.容腔调节器是由比例流量阀A1，储气罐R1 与换向阀A2组成.通过控制比例流量阀A1 调节进出调节器流量，起到等效调节被控环节容腔大小的作用.

1.2 容腔调节器数学模型

由质量守恒定律可得储气罐R1 的容腔流量微分方程［12］为

式中:qmr为流入容腔的流量;mr为容腔质量;V 为容腔体积;ρr为容腔内气体密度.

容腔调节器作用时气体流动一般处于亚声速流动状态，根据Sanville 的流量方程［13］，可知比例减压阀A1 的流量方程为

式中:Ur为阀口控制电压;br为阀口控制比例系数;k 为气体绝热指数;pr为容腔内压力;pa为调节器外端容腔压力;R 为气体常数;T 为容腔内温度;Ct为临界压力比，Ct=［2/(k+1)］k/(k-1).

由能量守恒定律可得储气罐压力微分方程［14］

式中:Cp为气体等压比热;Cv为气体等容比热;qmr为储气罐流量.

式(1)～(3)组成容腔调节器的数学模型.

2 钢轨打磨作业系统压力模型

2.1 系统结构组成

钢轨打磨作业系统应用于钢轨打磨列车单打磨系统作业过程中的压力输出部分，原理结构如图2 所示.气体由气源S1 经过储气罐R2 以及气动三联件A5 后，分别流入位于气缸有杆腔与无杆腔端比例减压阀A4 与A3.作业过程中控制A4 与A3 输出端压力实现打磨压力的输出. 容腔调节器安装在气缸无杆腔入口处，在打磨作业过程中，通过等效调节无杆腔容腔大小实现吸收压力波动.

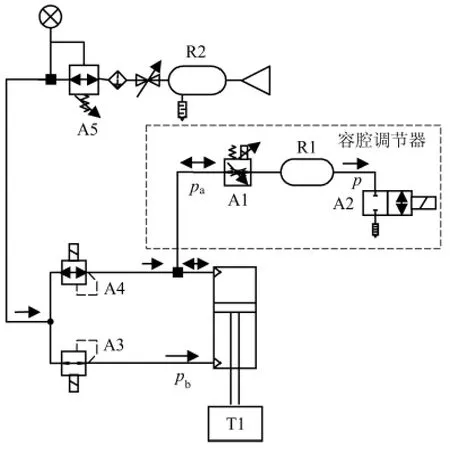
图2 打磨压力系统结构原理Fig.2 Structure diagram of the grinding pressure system

2.2 系统数学模型

(1)气缸活塞受力模型

式中:Aa、Ab分别为无杆腔和有杆腔压力作用面;pb为有杆腔端压力;m 为气缸活塞及打磨电机质量;θ 为气缸倾斜角度;F 为气缸输出打磨压力;a 为气缸活塞杆在外扰动下受迫运动的加速度;g 为重力加速度;f 为摩擦因数.

(2)气缸有杆腔模型

气缸受迫运动导致气缸容腔体积发生变化，在容腔模型中，将气缸容腔体积等效为初始体积与受迫变化体积两个部分.根据容腔流量微分方程与容腔压力微分方程，可得有杆腔流量模型为

式中:lb为有杆腔初始腔长;x 为容腔长度变化量;qmb为有杆腔流量.

(3)有杆腔端比例压力控制阀模型

有杆腔端控制阀为动铁式电气比例控制阀，根据牛顿第二运动定律可得比例阀阀芯力平衡方程［15］为

式中:ka为比例阀反馈弹簧等效刚度;xrb为阀芯位移量;ku为比例阀电系数增益;Ub为输出控制电压;Af为比例阀阀芯端部有效截面积.

根据Sanville 流量方程得到比例阀流量方程

式中:ωrb为阀口面积梯度;ψb为有杆腔流量参量.

(4)气缸无杆腔模型

将无杆腔容腔同样等效为初始体积与受迫变化体积两个部分.根据容腔流量微分方程与容腔压力微分方程得到有杆腔流量模型为

式中:la为有杆腔初始腔长;qma为流入气缸无杆腔端的气体流量

式中:qmw为无杆腔流量.

(5)无杆腔端比例压力控制阀模型

无杆腔端比例压力控制阀模型与有杆腔端相同.

比例阀阀芯力平衡方程为

式中:xrw为阀芯位移量;Uw为输出控制电压;pA为比例阀输出压力.

比例阀流量方程为

式中:ωrw为阀口面积梯度;ψa为无杆腔流量参量.

3 系统控制策略

系统采用双闭环控制方式，内环以气缸有杆腔压力作为反馈量，主要用于保障打磨气缸背压稳定;外环以气缸输出压力为反馈量，控制气缸打磨压力趋于恒定;容腔调节器在该过程中起到吸收扰动的作用，通过设计容腔调节器行为分析控制方案，保障系统整体控制性能.

3.1 容腔调节器行为分析控制

容腔调节器结构决定了其半主动气动执行模块的特性，根据调节器模型可知其行为受内外压差的限制.据此建立容腔调节器的行为控制策略

式中:Ure为反馈误差信号;Kr为误差比例;pseta为无杆腔设定压力.

(1)当无杆腔实际压力值大于正压设定值时，若容腔储气罐内压力值小于无杆腔压力值，则打开容腔调节器吸收气缸无杆腔压力为

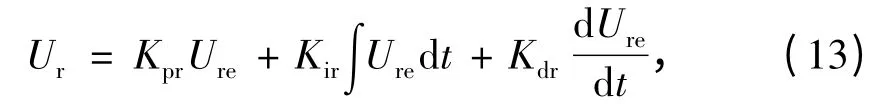
式中:Kpr为比例常量;Kir为积分常量;Kdr为微分常量.

(2)当无杆腔实际压力值小于正压设定值时，若容腔储气罐内压力大于无杆腔压力值，则打开容腔调节器加速无杆腔充气.若容腔储气罐内压力小于无杆腔压力值，则关闭容腔调节器降低充气损失.

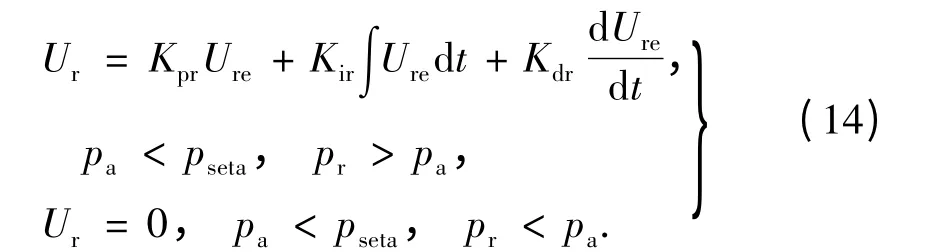
(3)当无杆腔实际压力值大于正压设定值且容腔储气罐内压力大于无杆腔压力值时，关闭容腔调节器流量阀打开换向阀快速释放调节器内压力至正常值.

3.2 内闭环背压稳定控制

考虑气缸无杆腔端压力除了维持输出压力外还具有缓冲打磨单元重力的作用，对其控制主要要求其抗扰动性，因此考虑采用带有扰动补偿的变结构控制策略实现对其稳定控制.

整理式(5)～(8)得到有杆腔压力模型为

式中:Nbu为有杆腔控制比例增益;Nbp为有杆腔压力比例系数;Nbr为无杆腔扰动比例增益.

令:u =NbuUb，f =Nbrdx/dt. 将有杆腔模型整理为

定义:pbn为设定目标压力;误差函数e =pbn-pb.误差函数微分方程为

选择滑模面为s=ce，设计滑模控制率为

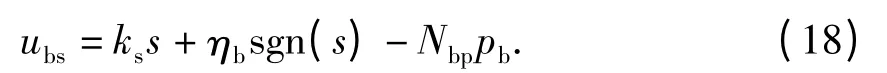
由式(18)可以看出，模型中的扰动量仅有一项f，在系统中添加扰动补偿项能够有效控制扰动量对控制器的影响.根据有杆腔处的压力模型可以建立扰动状态观测器，其表达式为

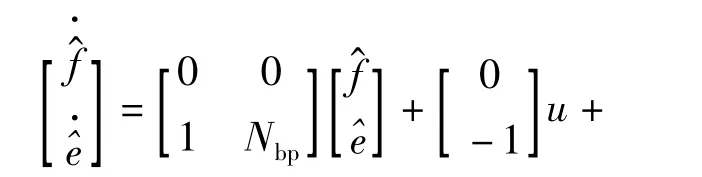
根据扰动估计量设计控制补偿项ubr，得到控制量:

定义李雅普诺夫函数为

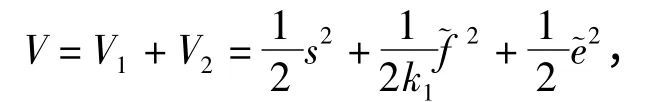
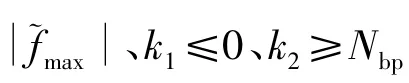
3.3 外闭环压力输出控制

气缸无杆腔端的压力主要是用于控制气缸压力输出.因此，对于气缸有杆腔端压力控制，需要能够根据反馈的打磨电流量迅速响应使打磨压力输出保持稳定.

整理式(4)、(9)～(13)，设等效输出压力

Fdx=F+Mgsin (θf)-Mg cos θ+pbnAb，得到有杆腔压力模型为

令θ=1/AaNbu，整理得到系统控制模型为

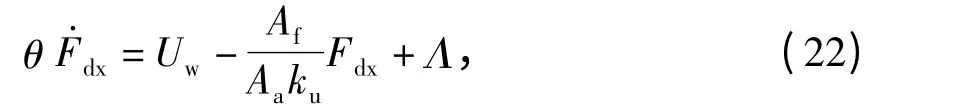
式中:Λ 为系统扰动参量.

对无杆腔的控制不仅表现在稳定性方面，还要求具有较高的准确性. 可以看出，系统扰动量的组成比较复杂，具有较强的不确定性.同时，由于扰动量中包含了配合控制的容腔调节器系统，使得对于无杆腔端比例阀的控制应具有适应变化的能力.将自适应控制与滑模变结构控制相结合能解决无杆腔压力控制中由于扰动量不确定以及系统非线性带来的问题.

令滑模面为

式中:e=Fdx-Fdxn，Fdxn为设定目标量;c 为滑模切换参量，c ＞0.

此时控制率设计为

控制率中的各项表示为:

(1)una为自适应补偿项，una=θ^⋅q;

(2)ubs1为反馈控制项，ubs1=-kss+AfFdx/Aaku;

(3)ubs2为鲁棒控制项，ubs2= -ηsgn(s).

定义李雅普诺夫函数为

4 系统仿真与分析

设计3 组对比性仿真实验:

(1)传统打磨压力控制系统，关闭容腔调节器，设定气缸有杆腔端比例阀为恒定控制量，根据反馈的输出压力对无杆腔端比例阀进行闭环调节;

(2)比例压力控制系统，关闭容腔调节器，控制器采集输出压力反馈值对无杆腔端比例阀PID控制，同时采集背压反馈值对有感腔端比例阀进PID 控制;

(3)单容腔调节压力控制系统，在传统打磨压力控制系统的基础上打开容腔调节器，根据设计的控制器控制相应阀进行压力输出.

4.1 阶跃扰动仿真

打磨列车在行车过程中，由于车体颠簸给系统带来扰动.利用阶跃扰动模拟打磨列车在打磨作业过程中受到的冲击，选用的外扰动阶跃信号幅值为10 mm，对4 种不同的系统进行对比仿真，得到阶跃扰动仿真曲线，如图3 所示.

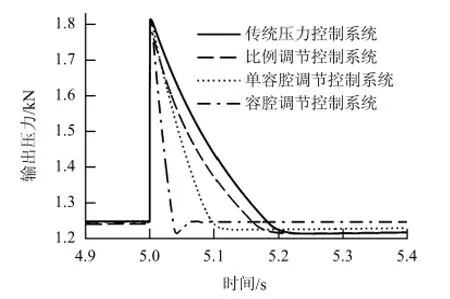
图3 阶跃扰动仿真曲线Fig.3 Simulation curve under step disturbance

由图3 可以看出，与其他3 组系统相比，容腔调节控制系统在面对阶跃扰动时响应速度最快;扰动发生后的调整过程带来4 个系统不同程度的控制超调，而容腔调节控制系统采用的控制策略使其能够快速消除超调，准确恢复到控制目标量.

4.2 波磨扰动仿真

利用正弦扰动模拟打磨列车在打磨作业过程中由于钢轨波磨作用带来的扰动［16］，选用的外扰动信号幅值为1.5 mm、频率为32 Hz，对4 个系统进行仿真，得到波磨扰动仿真曲线，如图4 所示.由图4 可以看出，容腔调节控制系统的压力波动情况最小.

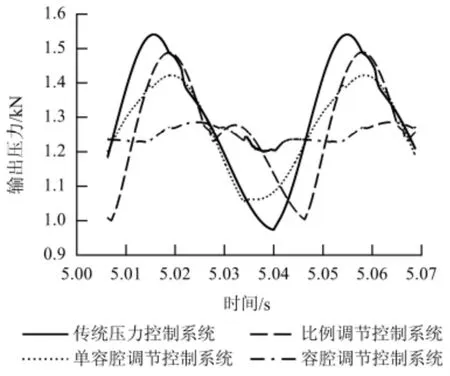
图4 波磨扰动仿真曲线Fig.4 Simulation curve under corrugation disturbance

分别对4 种系统进行正弦扰动幅值为1.5 mm、频率为0.5 ～50 Hz 的扫频，用输出压力标准差标定打磨压力的波动状况，得到的波磨扰动扫频仿真结果如图5 所示. 由图5 可知，4 组系统的打磨压力波动均随着扰动频率的增大而增大.在全频范围内，采用本文所研究的容腔调节控制系统取得较低的功率波动.

图5 波磨扰动扫频仿真结果Fig.5 Swept-frequency simulation results under corrugation disturbance

5 系统实验验证

建立如图6 所示的钢轨打磨试验台进行实验验证.试验台由拖车拖动打磨单元在试验轨上进行打磨作业，采用图2 所示的气动系统控制打磨压力.

图6 钢轨打磨试验台Fig.6 Rail grinding test bench

选取3 段状况相近的钢轨，分别采用传统打磨压力控制系统、单容腔调节压力控制系统以及容腔调节控制系统进行对比打磨实验，结果如图7 所示.由图7 可以看出，对比传统压力控制系统，增加容腔调节器能降低输出压力波动，而配合设计的控制策略使压力能一步降低.

表1 中为3 次打磨作业打磨压力的均值与标准差对比.

图7 打磨实验反馈压力对比Fig.7 Comparison of grinding feedback pressures

表1 实验结果对比Tab.1 Comparison of experimental results

由表1 可以看出，容腔调节器的作用使得打磨压力控制偏离目标值较大，而配合所设计的控制策略使其精度得到保障. 经计算可知，相比传统压力控制系统，本文所提出的容腔调节控制系统控制压力波动降低了76.8%.

6 结 论

(1)在传统钢轨打磨压力控制系统中加入容腔调节器能够有效降低作业过程中由于冲击扰动与波磨扰动带来的压力波动.

(2)容腔调节器的介入会导致系统控制精度降低，而配合所设计的控制策略能够在保证压力控制精度的前提下有效降低打磨压力波动.

(3)所研究系统可以通过在实际系统中安装容腔调节器来实现，具有很好的实用价值，利用设计的钢轨打磨试验台有效验证了该系统的性能.

［1］ 金学松，杜星，郭俊，等. 钢轨打磨技术研究进展［J］. 西南交通大学学报，2010，45(1):7-11.JIN Xuesong，DU Xing，GUO Jun，et al. State of arts of research on rail grinding［J］. Journal of Southwest Jiaotong University，2010，45(1):7-11.

［2］ 魏长竹，魏晨. 钢轨打磨车磨头数量及驱动方式分析［J］. 城市轨道交通研究，2010，13(12):85-88.WEI Changzhu，WEI Chen. Analysis on the gringing wheel quantity and the drive mode of rail gringing vehicle［J］. Urban Mass Transit，2010，13(12):85-88.

［3］ 张建峰，高新平，王卫东，等. 重载铁路钢轨打磨效果分析［J］. 铁道建筑，2009(4):104-105.ZHANG Jianfeng，GAO Xingping，WANG Weidong，et al. Analysis of heavy railway grinding effect［J］.Railway Engineering，2009(4):104-105.

［4］ 方立志，胡军科，周乾刚，等，钢轨打磨车恒力加载系统的分析仿真研究［J］. 铁道科学与工程学报，2012，9(2):115-118.FANG Lizhi，HU Junke，ZHOU Qiangang，et al.Analysis and simulation of the constant loading system of rail grinding train［J］. Journal of Railway Science and Engineering，2012，9(2):115-118.

［5］ NORITSUGU T，TAKAIWA M. Robust positioning control of pneumatic servo system with pressure control loop［C］∥IEEE International Conference on Robotics and Automation. Okayama:［s. n.］，1995:2613-2618.

［6］ PANDIAN S， TAKEMURA R. Pressure observer controller design for pneumatic cylinder actuators［J］.IEEE/ASME Transactions on Mechatronics，2002，7(4):490-499.

［7］ 刘忠，龙国键，褚福磊，等. 基于高速开关电磁阀技术的压力控制系统设计［J］. 液压与气动，2003(3):13-15.LIU Zhong，LONG Guojian，CHU Fulei，et al. The research of the pressure control system based on highspeed on-off valve［J］. Chinese Hydraulics ＆Pneumatics，2003(3):13-15.

［8］ 王雪松，程玉虎，彭光正. 电气比例阀自校正压力调节器的设计［J］. 电机与控制学报，2006，10(1):27-29.WANG Xuesong，CHENG Yuhu，PENG Guangzheng.A proposal of self-tunning pressure regulator for electropneumatic proportional pressure valve［J］. Electric Machines and Control，2006，10(1):27-29.

［9］ 车彦东，彭光正，钟圣国. 气动压力控制系统自校正控制的实用化研究［J］. 机床与液压，2006(7):143-144.CHE Yandong，PENG Guangzheng，ZHONG Shengguo.Application research of self-tuning technology in pneumatic pressure control system［J］. Machine Tool ＆Hydraulics，2006(7):143-144.

［10］ 李宝仁，刘浩，傅晓云，等. 密闭容腔压力伺服控制系统理论与实验研究［J］. 液压与气动，2004(7):1-3.LI Baoren，LIU Hao，FU Xiaoyun，et al. Theoretical and experimental research on pressure servo control system of closed chamber［J］. Chinese Hydraulics ＆Pneumatics，2004(7):1-3.

［11］ 聂蒙，李建勇，沈海阔，等. 钢轨打磨压力波动的影响机理［J］. 中南大学学报:自然科学版，2013，44(8):3576-3551.NIE Meng，LI Jianyong， SHEN Haikuo， et al.Grinding pressure fluctuation of rail grinding［J］.Journal of Central South University:Science and Technology，2013，44(8):3576-3551.

［12］ TAO Guoliang， WANG Xuanyin. The reaearch on electro-pneumatic-servo robot writing chinese calligraphy［C］∥2nd Internationals'Fluid Technisches.Dresden:［s. n.］，2000:4-16.

［13］ SANVILLE F E. A new method of specifying the flow capacity of pneumatic fluid power valves［C］∥Second Fluid power Symposium. ［S. l.］:BHRA，1997:37-47.

［14］ 陶国良，王宣银，路甬祥，等. 3 自由度气动比例/伺服机械手连续轨迹控制的研究［J］. 机械工程学报，2001，37(3):65-69.TAO Guoliang，WANG Xuanyin，LU Yongxiang，et al. Research on the continuous trajectory tracking control to pneumatic-servo robot with three-degree-of freedom［J］. Journal of Mechanical Engineering，2001，37(3):65-69.

［15］ 朱春波，包钢，聂伯勋，等. 用于气动伺服系统的自适应神经模糊控制器［J］. 机械工程学报，2001，37(10):79-82.ZHU Chunbo， BAO Gang， NIE Boxun， et al.Adaptive neural network fuzzy controller for pneumatic servo system［J］. Journal of Mechanical Engineering，2001，37(10):79-82.

［16］ 周跃清，田常海，张银花，等. 高速铁路钢轨打磨关键技术研究［J］. 中国铁道科学，2012，33(2):66-69.ZHOU Yueqing，TIAN Changhai，ZHANG Yinhua，et al. Research on key rail gringing technology of highspeed railway［J］. China Railway Science，2012，33(2):66-69.