检修车轨道导流板对流线型箱梁涡振的影响

刘 君， 廖海黎， 万嘉伟， 马存明

(1. 西南交通大学风工程试验研究中心，四川 成都610031;2. 西南交通大学风工程四川省重点实验室，四川成都610031)

随着桥梁建设技术的不断进步，越来越多的桥梁具有跨度大、重量轻、刚度小、阻尼小的特点，对风的作用也越来越敏感.大跨度桥梁，风致振动已不再是可以忽略的微小振动［1-2］，其抗风稳定性设计也越来越重要.涡激共振作为主梁最为常见的一种低风速下的风致振动，虽然不会导致桥梁直接损毁，但低风速下的长期振动会造成结构疲劳，并严重影响行车和行人的舒适性［3-5］.

涡激共振抑制措施主要分为构造措施和气动措施，构造措施有提高结构刚度、增大结构质量和结构阻尼等，气动措施有在主梁上设置风嘴、导流板、稳定板和抑流板等［6-7］.气动措施较构造措施具有经济实用、构造简单、抑振效果好等优点，是大跨度桥梁涡振抑制措施的首选.

不同形状的主梁断面气动性能差异较大，涡激共振抑振气动措施也不同［8］. 目前，主要通过风洞试验研究桥梁涡振的抑振措施［9］，文献［10］通过风洞试验研究得出了优化检修车轨道位置能明显减弱钢箱梁扭转涡振以及在风嘴处设置分流板能显著降低主梁竖向涡振响应. 文献［11］通过风洞试验研究证实在检修车轨道内侧设置导流板能有效减小扁平钢箱梁涡激振动振幅.通过风洞试验能较直观地对比研究不同的涡振抑振措施，但试验中对抑振措施的尝试具有一定的主观性和盲目性.

本文利用计算流体力学(CFD，computational fluid dynamic)对主梁断面进行流迹显示分析，通过涡脱规律确定对主梁断面涡激振动性能影响较大的构件［12］，着重围绕该部位展开抑振措施研究，能有效提高研究的针对性和准确性.文中以某大跨度斜拉桥流线型钢箱梁断面为例，通过1∶50 节段模型试验和CFD 计算分析，研究主梁涡激振动抑振措施. CFD 计算分析结果显示，检修车轨道附近涡脱规律明显，对主梁断面涡振性能影响较大［13］.围绕检修车轨道进行抑振措施试验研究，研究表明在检修车轨道内侧设置倾斜的导流板能有效地抑制涡激振动振幅.

1 涡振试验

某大跨度双塔斜拉桥采用流线型钢箱梁，涡振试验节段模型缩尺比为1∶50，试验在西南交通大学XNJD-1 风洞中第二试验段进行.

图1 为流线型钢箱梁横断面的示意，图2 为安装在风洞中的节段模型，表1 为节段模型主要试验参数.

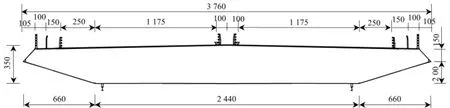
图1 主梁横断面示意图(单位:cm)Fig.1 Cross-section of main girder (unit:cm)

图2 风洞中的节段模型Fig.2 Section model in the wind tunnel

表1 节段模型主要试验参数Tab.1 Main test parameters of the section model

在均匀流场中进行涡激振动试验，成桥态-3°、0°及+3°风攻角下竖向涡振响应试验结果见图3.

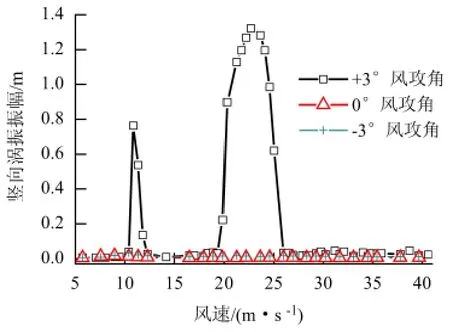
图3 竖向涡激振动响应Fig.3 Vertical responses of vortex-induced vibration

由图3 可知，主梁成桥态在-3°和0°风攻角下未发生大振幅涡振，在+3°风攻角下出现两个明显的竖向涡振区，两个涡振区的最大振幅分别为764、1 322 mm;两个涡振区间都处于较低风速，其最大振幅对应的风速分别为10.9、22.7 m/s，为桥位处常见风速.为保证大桥的运营结构安全性，需对主梁进行气动性能优化，研究涡振抑振措施.

2 CFD 流迹分析

大桥涡激振动抑振措施的研究主要方法是主梁节段模型风洞试验，但不同断面主梁的抑振措施可能存在较大差别，故抑振措施的试验研究往往存在一定的尝试性和盲目性. 计算机技术和CFD 方法的发展给风工程研究提供了一种可能代替风洞实验的手段，即“数值风洞”［14］. 借助CFD 方法对钝体(如桥面板、建筑结构等)周围的速度场和压力场进行分析，能形象地显示钝体外部绕流的特征和规律.

本文中采用商用CFD 软件Fluent 对横风作用下主梁断面二维流场进行瞬态的数值分析，计算域宽1 200 m，高400 m，边界层厚度1 mm，网格总数为168 024 个;湍流模型采用SST k-ω 模型［15］，时间步长取0.01 s. 提取不同时刻速度场的计算结果，进行流迹显示，分析涡脱规律寻找引起涡振的原因，确定引起主梁涡振的主要部位，便于有针对性的寻找抑振措施.图4 为主梁断面建模计算域网格划分图，图5 为主梁断面流场迹线图，图6 为主梁断面流场涡量等值线图.

图4 计算域网格划分Fig.4 Meshing of computational domain

图5 主梁断面流场迹线(+3°攻角)Fig.5 Pathline pattern around the girder section(+3° wind attack angle)

由图5 可以看出，+3°攻角来流经过主梁断面时，在迎风侧栏杆后面形成一个较大的漩涡，在该处桥面形成一个负压区，主要影响主梁的非定常气动力;在主梁底部，来流流经检修车轨道后形成一系列较小的均匀漩涡，对主梁产生涡激力.同时，从主梁断面流场涡量等值线可以清晰发现，在+3°风攻角来流中，检修车轨道后面出现了交替形成并脱落的漩涡，这样的漩涡容易激发主梁涡激共振. 从主梁断面的流场迹线及图6 分析可知，检修车轨道可能对主梁断面涡振影响较大，对无检修车轨道断面进行CFD 计算分析，流场涡量计算结果如图7所示.

图6 有检修道主梁断面流场涡量等值线(+3°攻角)Fig.6 Contours of vorticity magnitude around the section of girder with maintenance rails (+3° wind attack angle)

图7 无检修道主梁断面流场涡量等值线(+3°攻角)Fig.7 Contours of vorticity magnitude around the section of girder without maintenance rail(+3° wind attack angle)

对比图7 与图6 可以发现，有检修车轨道和无检修车轨道两种工况下，涡量等值线计算结果中主梁底板位置存在明显区别. 拆除检修车轨道后，主梁断面底部的漩涡完全消失，可知检修车轨道是引起主梁底部漩涡形成及脱落的主要构件，涡振抑振措施研究应该主要围绕检修车轨道进行.

3 抑振措施试验研究

为了验证CFD 的计算分析结果，将检修车轨道移除后再进行涡振试验. 试验结果显示，移除检修车轨道后，主梁在+3°、0°和-3°风攻角下均未出现明显涡激振动，表明引起主梁涡激振动的主要原因是位于大桥主梁底板的检修车轨道，对检修车轨道位置进行优化可以改善主梁的涡激振动性能.

针对引起涡振的检修车轨道，选择改变检修车轨道位置、在检修车轨道附近设置导流板等措施进行风洞试验测试，措施试验工况见表2，表中U 为来流方向.

3.1 检修车轨道对主梁断面涡振稳定性的影响

改变检修车轨道位置，从而改变气流通过检修车轨道的分离规律，研究不同位置的检修车轨道对主梁断面涡振稳定性的影响.试验分别对比研究了移除检修车轨道(工况1)、检修车轨道位于主梁斜腹板(工况2)及位于主梁底板(工况3、4)的情况.在-3°和0°风攻角下，各工况均未出现明显涡激振动，+3°风攻角下各工况试验结果如图8 所示.

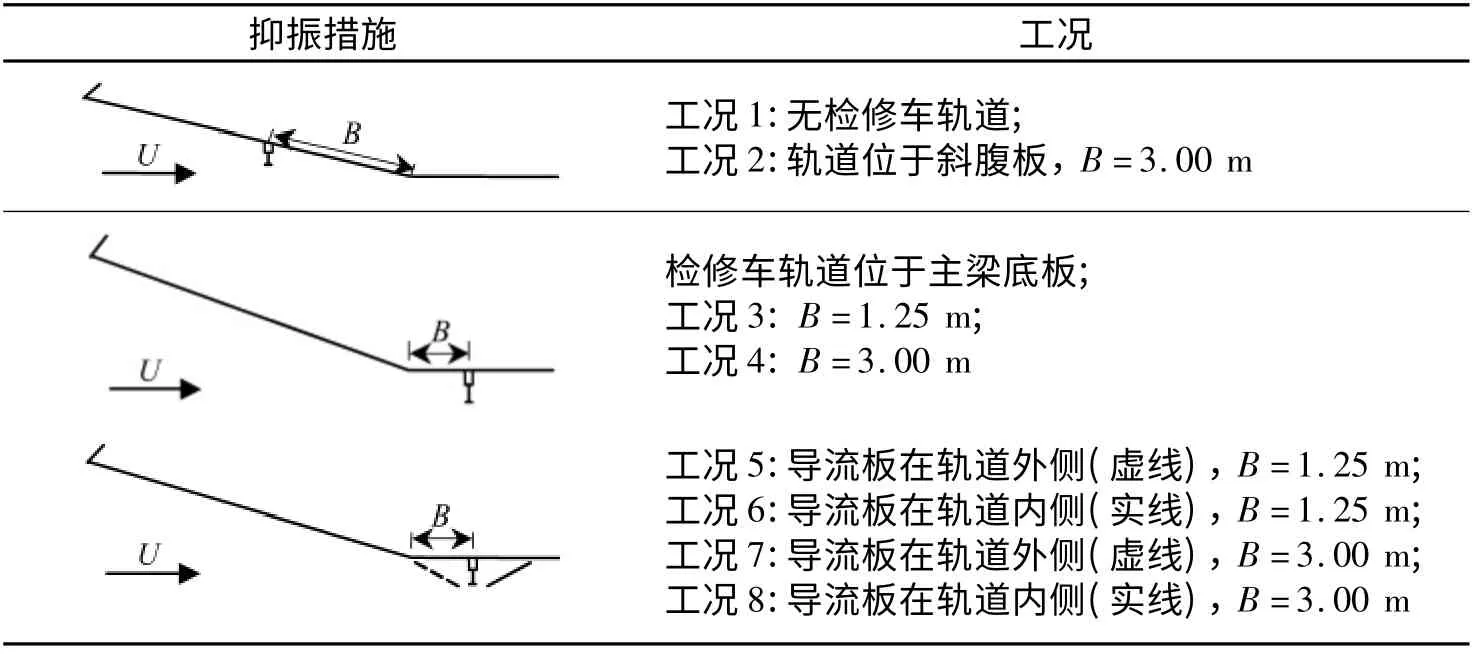
表2 涡振抑振措施Tab.2 Mitigation measures of vortex-induced vibration

图8 不同位置检修车轨道对应的涡振响应Fig.8 Responses of vortex-induced vibration for different maintenance rail positions

从图8(a)可知，拆除检修车轨道(工况1)，两个涡振区均消失，无明显涡振现象. 当检修车轨道位于主梁斜腹板(工况2)，主梁断面涡激振动锁定区间及振幅仅有微小改变，表明将检修车轨道移至斜腹板，对主梁的涡激振动影响很小.

从图8(b)可知，当检修车轨道位于主梁底板边缘1. 25 m 时(工 况3)，与 原 工 况 相 比，第1 个涡振区间内未出现明显涡振，但在第2 个涡振区间内涡振振幅没有减小.当检修车轨道位于主梁底板边缘3.00 m 时(工况4)，与原工况相比，第1 个涡振区间内未出现明显涡振，第2 个涡振区间内涡振最大振幅从1 322 mm 减小到800 mm.

3.2 设置导流板

改变检修车轨道在主梁上的位置，对主梁断面涡振性能有一定的优化作用，但对涡振的抑制作用较小.对于检修车轨道引起的涡激振动，借鉴国外Great Belt Bridge 以及我国苏通大桥的涡振抑振措施，尝试在检修车轨道附近设置导流板. 试验分别研究了在检修车轨道外侧(工况5、7)和检修车轨道内侧(工况6、8)设置导流板的工况，导流板宽1.00 m，与主梁底板夹角为30°.

各工况下主梁断面仅在+3°风攻角下发现涡振现象，试验结果与原工况对比如图9 所示.

从图9(a)可知，当检修车轨道位于底板边缘1.25 m 处，轨道外侧导流板(工况5)对主梁涡激振动无明显抑制作用，轨道内侧导流板(工况6)对主梁涡振性能有一定改善，使涡振最大振幅从1 310 mm 减小至850 mm.

由图9(b)可知，当检修车轨道位于底板边缘3.00 m 处，并在轨道外侧设置导流板(工况7)，主梁涡振区间和振幅与无导流板无明显区别;在轨道内侧设置导流板后(工况8)，主梁断面涡激振动得到有效抑制，在两个涡振区间内均未出现明显涡激 振动.

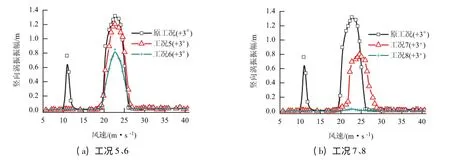
图9 设置不同位置导流板对应的涡振响应Fig.9 Responses of vortex-induced vibration for different guide vane positions

4 抑振机理初探

通过节段模型风洞试验发现，检修车轨道外侧导流板对主梁涡振无明显改善，而轨道内侧导流板则对涡振有良好抑制作用.通过Fluent 分别对导流板位于检修车轨道外侧和内侧的主梁断面进行二维断面数值分析，两断面在横风作用下涡量等值线见图10 ～11.

图10 导流板位于检修道外侧流场涡量等值线(+3°攻角)Fig.10 Contours of vorticity magnitude with guide vans set outside maintenance rails(+3° wind attack angle)

图11 导流板位于检修道内侧流场涡量等值线(+3°攻角)Fig.11 Contours of vorticity magnitude with guide vansset inside maintenance rails(+3° wind attack angle)

由图10 可知，导流板在检修车轨道外侧时(工况7)，流体流经导流板，再经上游检修车轨道后，仍然发生流动分离，分离后的流体在主梁底部再附着，并且在轨道与主梁底板交界处形成漩涡.发生再附着的流体流经下游检修车轨道后，在主梁底板尾部形成交替脱落的漩涡，且漩涡紧贴主梁底板，产生使主梁涡振的涡激力.

图11 为导流板位于检修车轨道内侧(工况8)的计算结果，虽然在上游轨道后面仍然形了漩涡，但由于轨道内侧导流板的存在，漩涡被引离主梁底面.同时在下游轨道处，轨道内侧导流板抑制了漩涡的产生，在主梁尾部未出现明显的漩涡. 故轨道内侧导流板能有效减小主梁涡激力，抑制主梁涡激振动.

为更加直观地对比分析导流板分别设置于检修车轨道内侧和外侧的区别，通过Fluent 分别计算得出两种工况下主梁断面升力系数时程，计算结果如图12 所示.

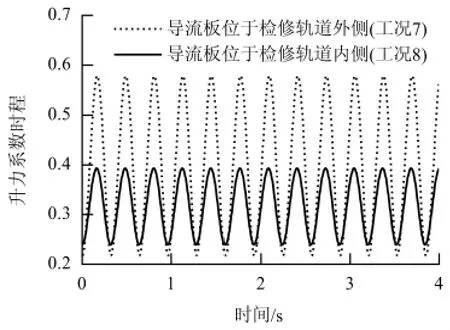
图12 主梁断面升力系数时程结果Fig.12 Time-history curves of lift coefficients of the girder section

由图12 可以看出，导流板位于检修车轨道外侧时，主梁升力系数均方根值明显大于导流板位于检修车轨道内侧工况.在不考虑主梁运动引起的气动力的情况下，主梁竖向涡振振幅与所受升力大小成正相关［16］，故对应于较小升力的工况8(导流板位于检修车轨道内侧)对主梁涡激振动抑制效果明显优于工况7(导流板位于检修车轨道外侧).

综合对比以上CFD 数值模拟和风洞试验结果，可以看出有检修车轨道和移除检修车轨道情况下，CFD 计算主梁断面流场涡量得到的结果截然不同(如图6 ～7).检修车轨道的存在引发了周期性形成并脱落的漩涡，这与风洞试验中有检修车轨道工况下主梁涡振响应远大于无检修车轨道工况结果一致.导流板分别位于检修车轨道外侧和内侧工况下主梁流场涡量计算结果也存在显著区别(如图10 ～11)，与风洞试验中两种导流板具有明显不同的涡振抑制效果一致.与风洞试验结果的对比，说明了通过CFD 数值模拟研究流线型箱梁涡振抑制措施具有较好的正确性和实用性.

5 结 论

(1)检修车轨道对流线型钢箱梁断面涡振性能具有较大影响，易引发或增大流线型钢箱梁断面涡激振动振幅.

(2)检修车轨道位置对流线型钢箱梁涡振振幅有一定影响，改变其位置能一定程度上减小涡激振动振幅，但减小幅度有限.

(3)在检修车轨道内侧设置导流板能大幅度减小流线型钢箱梁涡激振动振幅，具有良好的抑振效果，但轨道外侧导流板对主梁涡振振幅无明显抑制作用.

(4)通过CFD 对设置抑振措施的主梁断面建模计算分析，定性分析导流板的抑振机理，表明在检修车轨道内侧设置导流板，可以将主梁底部上游检修车轨道引起的漩涡引离主梁底板，并且抑制下游检修车轨道处的漩涡产生，有效地减小涡激力，抑制主梁涡激振动.

需要说明，以上结论是在本文的主梁断面基础上研究得出，可为类似桥梁断面提供参考，并不一定适应所有流线型箱梁断面.同时本文仅对导流板抑振机理进行了定性分析，更为准确的抑振机理定量分析还有待进一步的探索与研究.

［1］ 徐洪涛，廖海黎，李明水，等. 坝陵河大桥节段模型风洞试验研究［J］. 世界桥梁，2009，30(4):30-33.XU Hongtao，LIAO Haili，LI Mingshui，et al. Wind tunnel test study of sectional model of Baling River Bridge［J］. World Bridges，2009，30(4):30-33.

［2］ LARSEN A ，SAVAGE M，LAFRENIERE A，et al.Investigation of vortex response of a twin box bridge section at high and low Reynolds numbers［J］. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(6):934-944.

［3］ 鲜荣，廖海黎，李明水. 大跨度桥梁主梁沿跨向涡激振动响应计算［J］. 西南交通大学学报，2008，43(6):740-746.XIAN Rong，LIAO Haili，LI Mingshui. Calculation of spanwise vortex-induced vibration responses of long-span bridge girder［J］. Journal of Southwest Jiaotong University，2008，43(6):740-746.

［4］ 陈政清. 桥梁风工程［M］. 北京:人民交通出版社，2005:129-130.

［5］ 鲜荣，廖海黎，李明水. 大比例主梁节段模型涡激振动风洞试验分析［J］. 实验流体力学，2009，23(4):15-20.XIAN Rong，LIAO Haili，LI Mingshui. Analysis of vortex induced vibration of large-scale section model of girder in wind tunnel［J］. Journal of Experiments in Fluid Mechanics，2009，23(4):15-20.

［6］ 刘健新. 桥梁对风反应中的涡激振动及制振［J］. 中国公路学报，1995，8(2):74-79.LIU Jianxin. Vortex induced vibration and its control in responses of bridge to wind［J］. China Journal of Highway and Transport，1995，8(2):74-79.

［7］ 孙延国，廖海黎，李明水. 基于节段模型试验的悬索桥涡振抑振措施［J］. 西南交通大学学报，2012，47(2):218-223.SUN Yanguo，LIAO Haili，LI Mingshui. Mitigation measures of vortex-induced vibration of suspension bridge based on section model test［J］. Journal of Southwest Jiaotong University，2012，47(2):218-223.

［8］ SARWAR M W，ISHIHARA T. Numerical study on suppression of vortex-induced vibrations of box girder bridge section by aerodynamic countermeasures［J］.Journal of Wind Engineering and Industrial Aerodynamics，2010，98(12):701-711.

［9］ 徐泉，王武刚，廖海黎，等. 基于大尺度节段模型的悬索桥涡激振动控制气动措施研究［J］. 四川建筑，2007，27(3):110-112.

［10］ 李永乐，侯光阳，向活跃，等. 大跨度悬索桥钢箱主梁涡振性能优化风洞试验研究［J］. 空气动力学学报，2011，29(6):702-708.LI Yongle，HOU Guangyang，XIANG Huoyue，et al.Optimization of the vortex induced vibration for steel box girder of long span suspension bridges by wind tunnel test［J］. Acta Aerodynamica Sinica，2011，29(6):702-708.

［11］ 朱思宇，李永乐，申俊昕，等. 大攻角来流作用下扁平钢箱梁涡振性能风洞试验优化研究［J］. 土木工程学报，2015，48(2):79-86.ZHU Siyu， LI Yongle， SHEN Junxin， et al.Optimization of vortex-induced vibration of flat steel box girders at large attack angle by wind tunnel test［J］. China Civil Engineering Journal，2015，48(2):79-86.

［12］ 朱佳琪. 基于CFD 的桥梁涡激振和颤振气弹模拟研究［D］. 成都:西南交通大学，2013.

［13］ SIMIU E， ROBERT H S. Wind effects on structures［M］. New York:John Wiley ＆ Sons，1978:216-218.

［14］ DEFRAEYE T，BLOCKEN B，KONINCKX E，et al.Aerodynamic study of different cyclist positions:CFD analysis and full-scale wind-tunnel tests［J］. Journal of Biomechanics，2010，43(7):1262-1268.

［15］ MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications［J］. AIAA Journal，1994，32(8):1598-1605.

［16］ 刘仰昭. 倒角方形桥塔气动性能风洞试验及减振措施研究［D］. 成都:西南交通大学，2013.