计算连续型随机变量线性组合分布的Laplace变换法
2020-04-29赵书银张礼刚马丽红武小云
赵书银 张礼刚 马丽红 张 新 武小云
(河北建筑工程学院理学院,河北 张家口 075000)
0 引 言
随机变量的函数的分布是概率统计中的重要知识点.连续型随机变量的函数的概率密度的计算的通用方法是使用定义先求其分布函数,再求导得到概率密度,计算量较大.特殊情况是,多个相互独立的连续型随机变量的和的概率密度可以通过卷积运算实现.文献[1]利用Fourier变换提供了一种算法,能计算多个相互独立的连续型随机变量线性组合的概率密度而且避免计算卷积.但是Fourier变换不仅要用到复数,而且很多常见的函数的Fourier变换都是广义函数.本文对相互独立的有界连续型随机变量的线性组合和非负连续型随机变量的正系数线性组合,使用Laplace变换及其逆变换,得到了计算效率更高的一种计算方法.
1 主要结论
因为Laplace变换要求函数在(-∞,0)上取值为0,所以要对概率密度函数的支集包含负数的函数进行处理,以使得其含于[0,+∞].为此需要对随机变量进行平移和缩放的操作.这里考虑Y是X的一次函数的结果,给出以下定理.
定理1 设随机变量X的概率密度为f(x),则Y=kX+b(k≠0)的概率密度为
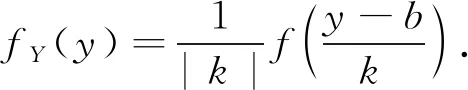
(1.1)
证明以k<0为例,此时Y的分布函数
于是有
当k>0时同理.证毕.
所以当有界随机变量X的概率密度函数的支集含有负数时,因X有界,设f(x)在(-∞,b]上等于0,则可以通过变换Y=X-b,使得Y的概率密度函数fY(y)=f(y+b)在y∈(-∞,0]上等于0,这样就可以对fY(y)使用Laplace变换,如果需要还原X的概率密度,只需把fY(y)中的y替换成x-b就行了.


(1.2)
或写为

(1.3)

证明当n=2时,
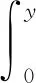
其中*表示两个函数的卷积运算.由Laplace变换的卷积性质,有

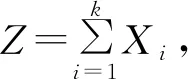


可见(1.2)成立.
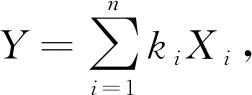

(1.4)
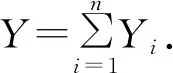



两边取Laplace逆变换,就得到(1.4).
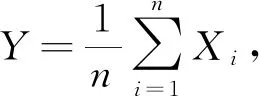

(1.5)

2 算法的意义和应用
在文献[1]中,给出了这个问题的Fourier变换法,Laplace变换法和Fourier变换法对相互独立的有界连续型随机变量和非负随机变量都能有效且可靠地求出它们的线性组合的概率密度.但是三者的计算效率差距很大,在符号计算软件maple中取n=300时,计算相互独立的参数都是1的指数分布之和的概率密度,所用的时间见下表.

表2-1 三种算法用时表
从表中可见使用Fourier变换的计算速度是直接使用卷积运算速度的163倍还多,这得益于Fourier变换能够把卷积运算变为乘法运算.而这里给出的Laplace变换法在此基础上进一步提高了运算效率,又把速度提高了5.5倍.所以在求解相互独立的随机变量的线性组合的概率密度时,如果能使用Laplace变换,那么Laplace变换的计算效率是最高的.
3 算法的局限性
求相互独立的连续型随机变量的概率密度,原始的方法是进行卷积运算.Fourier变换和Laplace变换都能把卷积运算变为乘积运算,从而提高计算效率.但是Laplace变换只能对支集非负的函数运算.对连续型随机变量而言,要求其取值也非负.Fourier变换则没有这种局限性.本文提供的算法可以避免这种约束,保证对有界的情形也能使用Laplace变换,但是连续型随机变量的取值没有下界时还是无法使用.
