高速平面并联机器人动态分析与实验*

2015-01-12高名旺张宪民山东理工大学机械工程学院淄博55049华南理工大学机械与汽车工程学院广州5064

振动、测试与诊断 2015年4期

高名旺，张宪民（.山东理工大学机械工程学院淄博，55049）（.华南理工大学机械与汽车工程学院广州，5064）

高速平面并联机器人动态分析与实验*

高名旺1，张宪民2
（1.山东理工大学机械工程学院淄博，255049）
（2.华南理工大学机械与汽车工程学院广州，510641）

基于弹性动力学和实验对高速轻型平面并联机器人的动态响应进行研究。首先，根据机构的几何和惯性非线性建立机构运动微分方程组，对机构的两个典型位形的动态响应进行分析；其次，建立了由3-RRR轻型并联机构和控制系统组成的实验装置，对理论分析进行了验证。结果表明，在位形2，理论分析和实验一致，即机构的残余振动很快衰减；在位形1，理论分析与实验两者不同，实验测量的动态响应为自激振动，而数值仿真得到衰减的残余振动。同时，结果也表明机构在不同位形有不同的动态响应。

平面并联机器人；高速；弹性动力学；残余振动

引言

和串联机构相比，并联机构具有高定位精度、更高的加速度和负载能力等［1］优点，因而应用广泛；然而并联机构在工作空间的动态特性非常复杂［2］，这给机构的设计和使用造成很大困难。轻量化的并联机器人在高速、高加速工作时，杆件的弹性变形容易导致系统整体弹性振动，从而影响机构的应用。弹性动力学广泛用于模拟串联机器人和四杆机构［3］，也逐渐用于并联机构分析。文献［4］利用虚功原理对柔性五杆机构建立动力学模型并实验验证。Zhou等［5］运用有限元法建立柔性3-PRS机构的动力学公式并分析其振动特性。Wang等［6］和Zhang等［7］分别运用有限元法和假定模态法对3-PRR机构建立动力学模型，并对其进行了主动振动控制研究。刘善增等［8］对3-RRC并联机器人建模分析其动态特性。Zhao等［9］运用有限元方法模拟分析六自由度并联机器人的动态特性。Rognant等［10］提出一种建立并联机构弹性动力学模型的步骤。然而，以上研究在不同位形、高速运动对并联机构动态特性影响的分析，尤其是实验研究相对较少［11］。

笔者基于有限元法建立3-RRR机构的弹性动力学模型，在工作空间内对不同位形的动态特性进行研究。首先，利用弹性动力学模型对机构的两个典型位形的动态特性进行分析；然后，利用实验装置对两个典型位形的动态特性进行测试。结果表明，在位形2位置，仿真结果和实验结果一致，而位形1的仿真结果和实验结果有较大差异。该研究结果为机器人的运动规划和控制提供参考。

1 3-RRR机构弹性动力学模型

如图1所示，3-RRR平面并联机器人由动平台、静平台和链接两者的支链组成。支链由铰和连杆组成，其中：铰包含主动铰Oi、被动铰Bi和Ci；连杆分别为主动杆OiBi和被动杆BiCi。假设连杆为柔性杆，其余元件为刚性体。惯性坐标系O-xy建立在静平台上，坐标系原点在三角形O1O2O3的形心，z轴按右手螺旋确定。

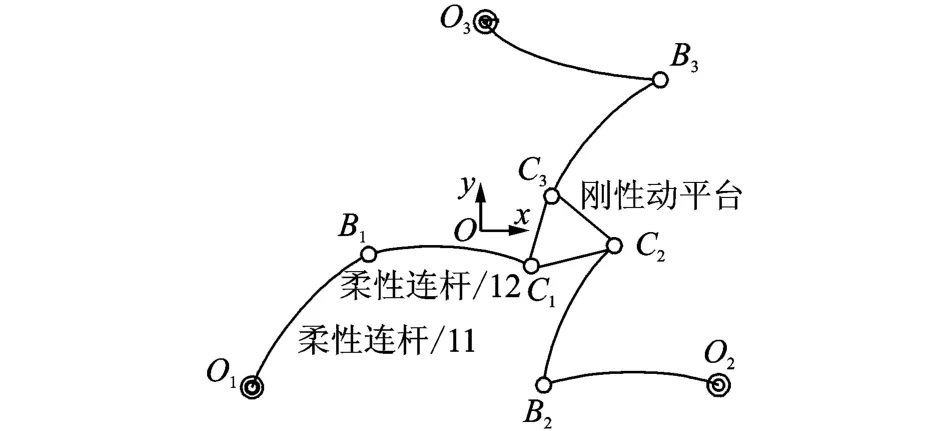
图1 3-RRR机构Fig.1 3-RRR mechanism

1.1 单元位移

柔性连杆的运动用等效刚体模型描述［12］。平面梁单元如图2所示。实线部分为弹性变形单元，虚线部分为假设的刚体未变形单元。单元坐标系为a-xy，x轴为刚体单元中性轴方向，原点在刚体单元的端点a。

弹性体的横向变形采用三次Hermit多项式［13］，轴向弹性位移采用线性插值函数。弹性体中任意一点的弹性位移在单元坐标系中可表示为

其中：ue为梁单元位移向量；Ne为梁单元形函数；r为弹性体中C点相对瞬态刚体运动的弹性位移向量，式中向量左上标e表示在单元坐标系中表示。

位置向量可写成如下形式

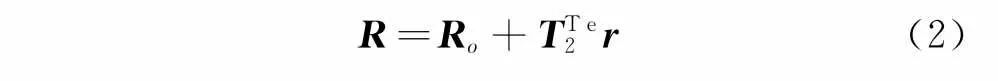
其中：Ro为C点在刚性单元中对应的点的坐标向量；T2为惯性坐标系到单元坐标系的2×2矩阵。对式（2）两边求导可得C点速度

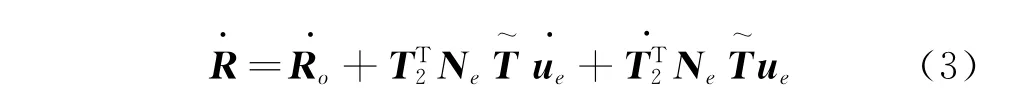
其中：T为惯性坐标系联系单元坐标系的6×6常数矩阵；T～

表示公式求导。

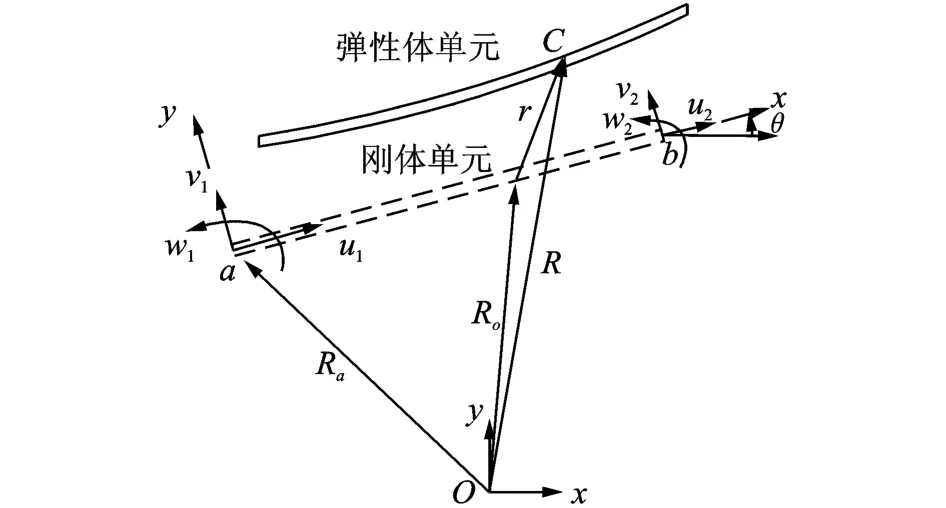
图2 欧拉-伯努利单元Fig.2 Euler-Bernoulli element

1.2 支链的动能和势能

支链中的连杆由3部分组成，即连杆两端的集中质量和中间的柔性杆。笔者把柔性杆作为一个柔性单元，连杆两端集中质量的动能分别合并到动平台和被动铰Bi单元的动能中。支链的动能为

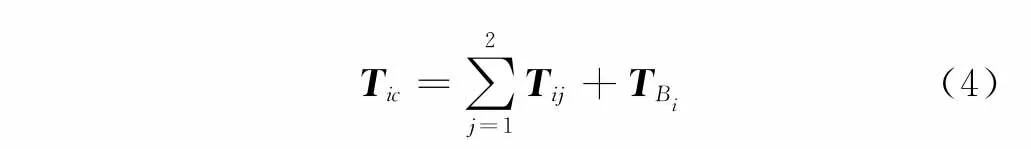
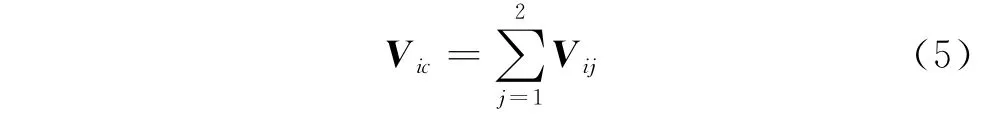
其中：Vij为第i支链第j连杆的势能。

1.3 全局坐标

系统的全局坐标如图3所示，总共取18个节点坐标。系统全局坐标可表示为

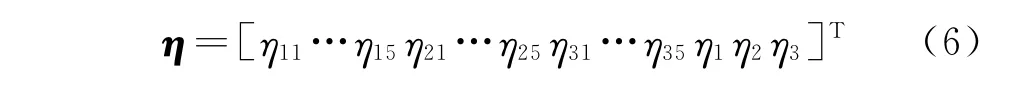
其中：Tic为第i支链的动能；Tij为第i支链第j连杆的动能；TBi为第i支链被动铰Bi的动能。

支链的势能为

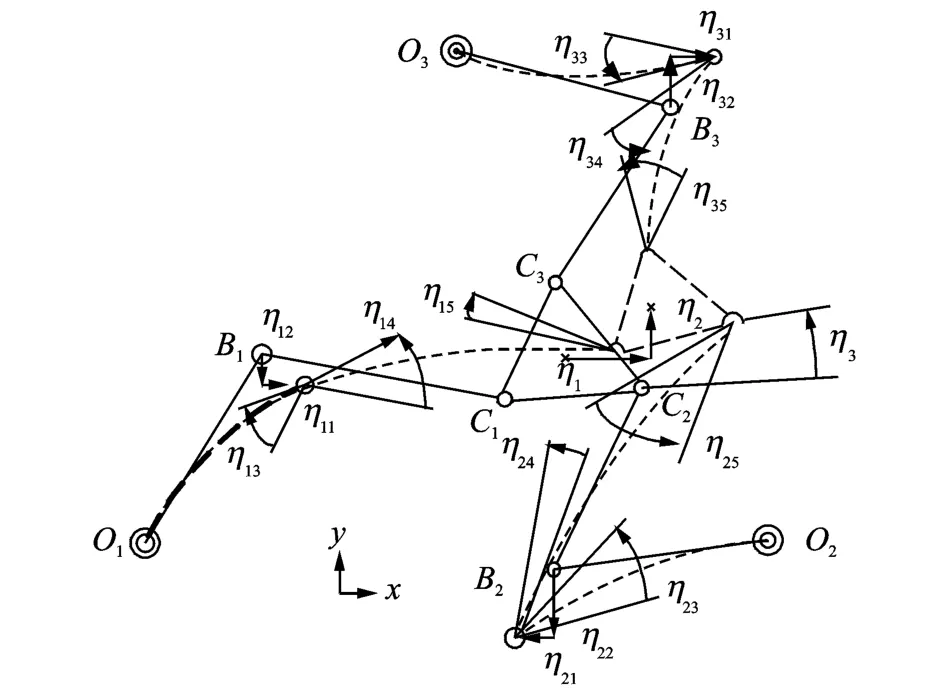
图3 全局坐标Fig.3 Global coordinate

单元位移向量和全局坐标的映射由连接矩阵Si1，Si2，SBi和Sp实现。

单元i1的位移向量与全局坐标的关系为

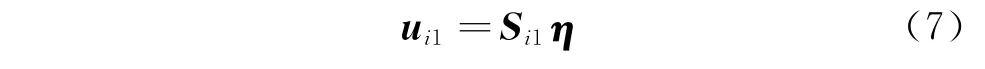
单元i2的位移向量与全局坐标的关系为

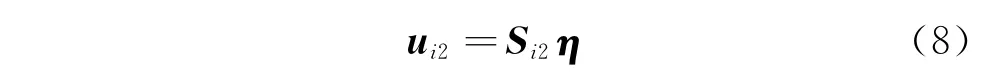
单元Bi的位移向量与全局坐标的关系为

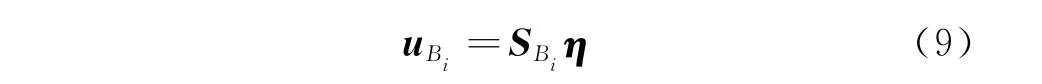
动平台的位移向量和全局坐标的关系为

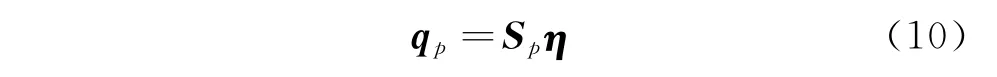
1.4 系统动力学模型

1.4.1 动力学模型

考虑刚体运动对弹性振动的影响，因而机构的拉格朗日等式可用系统的柔性全局坐标表示，则3-RRR机构的运动等式为

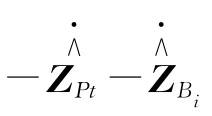
1.4.2 增加比例阻尼的系统动力学模型

通常在有限元分析中，使用比例阻尼模拟结构阻尼，比例阻尼是质量矩阵和刚度矩阵的线性组

其中：Tp为动平台的动能。

把式（4），（5），（7）～（10）分别代入式（11），整理并写成矩阵形式为合［14］，即增加比例阻尼后动力学模型可表示为

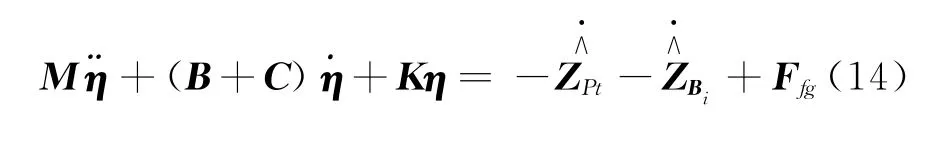
2 数值仿真

为研究机构在工作空间不同位形的动态特性，以机构的两个典型位形为例进行运动响应研究。利用弹性动力学模型对机构在典型位形的动态响应进行仿真分析。并联机构的杆件采用铝合金，材料弹性模量为0.7×105MPa，材料密度为2.7×103kg/m3，主要参数如表1所示。

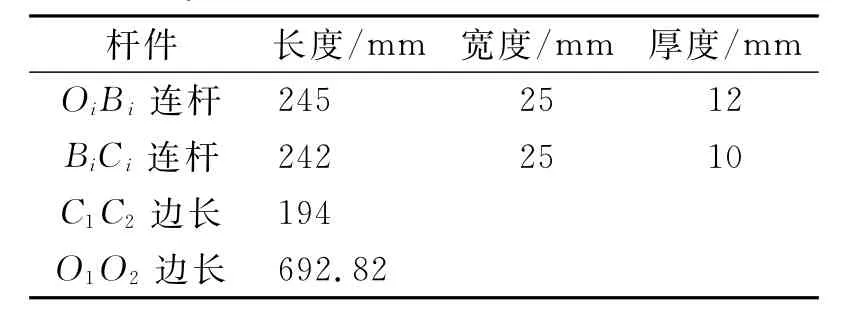
表1 机构连杆参数Tab.1 Parameters of mechanism link

2.1 位形1的残余振动仿真分析

位形1（0.15 m，0）如图4所示。机构以梯形速度规划从原点移动到点（0.15 m，0），其加速度为20 m/s2，速度为1 m/s。此位移被称为轨迹1，具体位移规律为

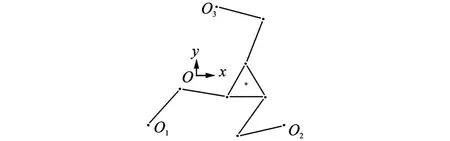
图4 位形1Fig.4 Configuration one

其中：a为运动加速度；x，y分别表示x，y轴方向的位移规律；φ表示绕z轴的转动规律。

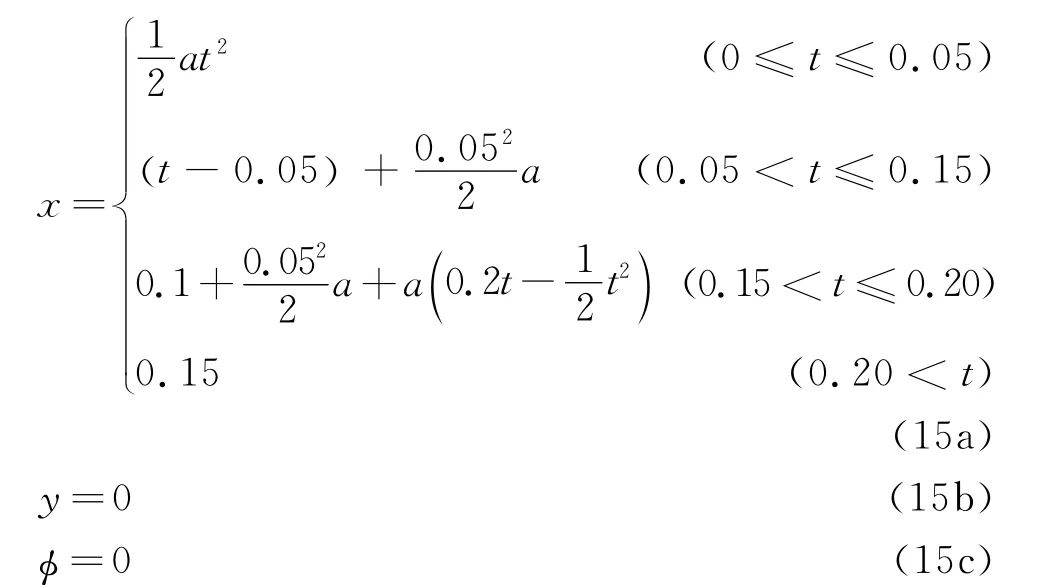
式（15）描述了机构在0.2 s内沿x轴从原点移动到点（0.15 m，0）。为更好地比较机构在位形1的动态特性，在Matlab/Simulink中编程并运行0.5 s。动平台的动态响应如图5和图6所示，分别表示机构在x轴和y轴的振动位移。

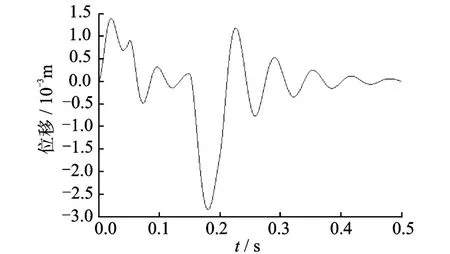
图5 位形1的x轴振动位移Fig.5 Vibration of x direction at configuration one

图6 位形1的y轴振动位移Fig.6 Vibration of y direction at configuration one

由图5可看到，在加速阶段，即0≤t≤0.05 s，机构受到较大冲击，x轴的振动幅值为1.39 mm。在匀速阶段，即0.05＜t≤0.15 s，振动幅值减少。在减速阶段，即0.15＜t≤0.2 s，振动幅值又增加，达到2.85 mm，此时机构的刚度变小，从而导致弹性变形增大。最后，当t＞0.20 s时，运动响应为残余振动，其幅值为1.18 mm，并且逐渐衰减。由图6看到，在各个阶段，机构在y向的振动幅值都较小，幅值为0.44 mm，尤其是残余振动振幅小，为0.15 mm，衰减快说明x向扰动对y方向的影响较小。

2.2 位形2的残余振动仿真分析

位形2如图7所示，即点（-0.15 m，0），是位形1的对称位形。轨迹2为机构从原点沿x轴运动到点（-0.15 m，0）。机构位移规律如式（16）所示。

图7 位形2Fig.7 Configuration two

式（16）描述了机构在0.2 s内沿x轴从原点移动到位形2，移动速度和加速度与前面一致。动平台的动态响应如图8，9所示。图8为x轴振动位移。图9为y轴振动位移。

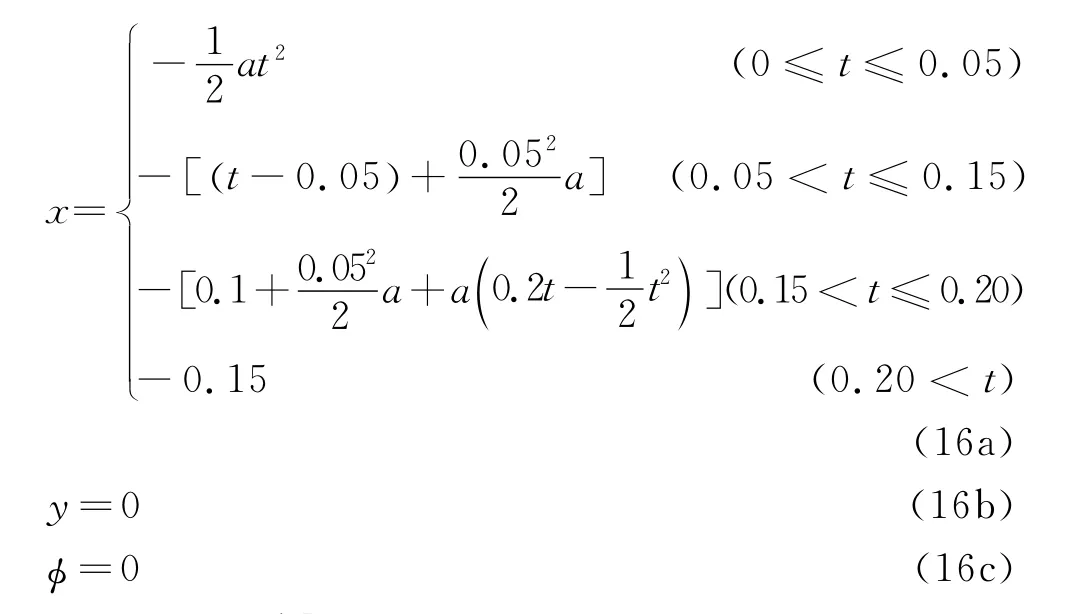
图8 位形2的x轴振动位移Fig.8 Vibration of x direction at configuration two

从图8可知，在加速阶段，x轴的振动幅值较大，达到1.33 mm。在匀速运动阶段，振动幅值减少。在减速运动时，幅值为0.81 mm，比加速阶段的幅值小。最后，运动到达指定点后，即t＞0.20 s时，机构的残余振动幅值仅为0.19 mm且很快衰减。

在图9中，y轴各阶段的振动幅值都较小，加速阶段y向振动幅值仅为0.09 mm，说明在此阶段x轴的力扰动对y轴的影响较小，同时也表明此时其y轴刚度大；在减速阶段，y轴产生的振动幅值为0.73 mm，比加速时大，意味着机构在y轴的刚度变小了；最后，机构残余振动的幅值为0.28 mm。

图9 位形2的y轴振动位移Fig.9 Vibration of y direction at configuration two

图5与图8比较可知，位形1的残余振动幅值比位形2的大，说明机构在位形1的刚度小，振动超调量大。图6和图9比较可知，不同的方向有不同幅值的残余振动，说明机构在某一位形的不同方向的刚度也不同。

3 实验

3-RRR实验设备如图10所示，设备包含并联机构、伺服电动机和dSPACE控制器。3-RRR机构由铝合金制成的轻型连杆、动平台和基座组成，连杆之间用滚动轴承连接。3个交流伺服电动机被固定在基座上，其额定转速为3 kr/min。在Matlab/Simulink中编好程序，然后下传到dSPACE中，通过伺服电动机控制机构运动。

机构的运动速度为1 m/s，加速度为20 m/s2。机构的动态响应用动平台的位移表示，动平台的位移由激光干涉仪XL-80测量得到。轨迹1的实测位移如图11所示。可以看到，机构的残余振动振幅由1.63 mm逐渐增大至3.57 mm，最后形成幅值固定的有规律的振动，这种振动为自激振动。这种现象和图5的仿真结果有所不同，因为机器人发生机电耦合作用。机构在此位形的残余振动诱发了伺服系统，伺服系统成为机构的激励源，从而形成了自激振动。图12为位移1的速度变化规律，该图清楚地表明自激振动的发生和发展。

图10 3-RRR机构照片Fig.10 Photo of the 3-RRR manipulator

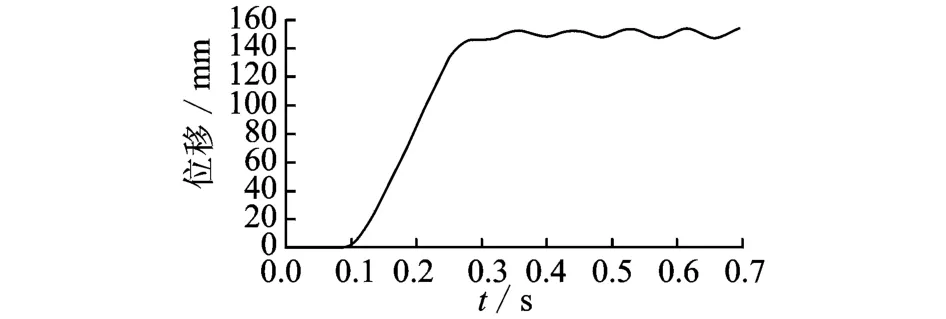
图11 轨迹1的动态响应Fig.11 Dynamic response of trajectory one

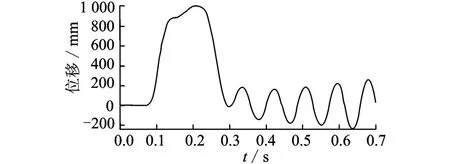
图12 轨迹1的速度Fig.12 Velocity of trajectory one

轨迹2的实测位移如图13所示，机构的残余振动的幅值为0.14 mm且很快衰减。与图10相比，振动非常小，因而机构在位形2的动态性能更好。与图8相比，两者的残余振动幅值相近，相差0.05 mm。实验证明理论模型能模拟机构的动态响应。

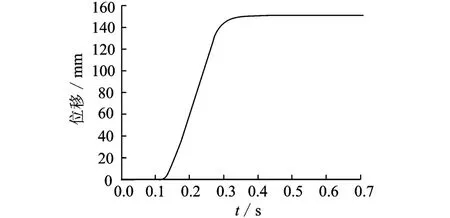
图13 轨迹2的动态响应Fig.13 Dynamical response of trajectory two

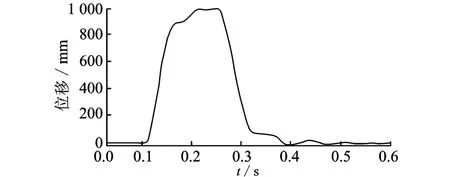
图14 轨迹2的速度Fig.14 Velocity of trajectory two

由图14的速度变化可以清楚地看到机构的残余振动变化规律。图12和图14比较发现，机构在位形1的残余振动较大且不断增大，形成自激振动，在位形2的残余振动幅值小且衰减很快。

4 结束语

动力学模型能较好地模拟机构的残余振动，但不能正确地模拟实际机器人的自激振动。模拟和实验表明并联机器人在不同位形的残余振动有很大不同。有的位形超调量大，而且会形成自激振动，有的位形超调量小，因而在应用并联机构时要考虑在不同位形的动态响应，避免较大的位置误差。仿真可以看出，机构在同一位形时，不同方向的动态响应也不同，因此实际应用时要考虑机构的运动方向。

［1］ Merlet J R.Parallel robots［M］.2nd ed.Netherlands：Springer，2006：20-23.

［2］ Piras G，Cleghorn W L，Mills J K.Dynamic finite-element analysis of a planar high-speed，high-precision parallel manipulator with flexible links［J］.Mechanism and Machine Theory，2005（40）：849-862.

［3］ Giovagnovi M.Dynamics of flexible closed-chain manipulator［C］∥ASME Design Technical Conference.［S.l.］：America Society of Mechanical，1992，69（2）：483-490.

［4］ Gasparetto A.On the modeling of flexible-link planar mechanisms：experimental validation of an accurate dynamic model［J］.Journal of Dynamic Systems，Measurement and Control，2004，126：365-375.

［5］ Zhou Zili，Xi J，Mechefske C K.Modeling of a fully flexible 3-PRS manipulator for vibration analysis［J］.Journal of Mechanical Design，2006，128：403-412.

［6］ Wang Xiaoyun，Mills J K.Dynamic modeling of a flexible link planar parallel platform using a substructuring approach［J］.Mechanism Machine Theory，2006，41（6）：671-687.

［7］ Zhang Xuping，Mills J K，Clehorn W L.Coupling characteristics of rigid body motion and elastic deformation of a 3-PRR parallel manipulator with flexible links［J］.Multibody System Dynamics，2009，21：167-192.

［8］刘善增，余跃庆，刘庆波，等.3-RRC并联机器人动力学分析［J］.机械工程学报，2009，45（5）：220-224.Liu Shanzeng，Yu Yueqing，Liu Qingbo，et al.Dynamic analysis of 3-RRC parallel manipulator［J］.Journal of Mechanical Engineering，2009，45（5）：220-224.（in Chinese）

［9］ Zhao Yongjie.Dynamics analysis and characteristics of the 8-PSS flexible redundant parallel manipulator［J］.Robotics and Computer-Integrated Manufacturing，2011，27：918-928.

［10］Rognant M E，Courteille E，Maurine P.A systematic procedure for the elastodynamic modeling and identification of robot manipulators［J］.IEEE Transactions on Robotics，2010，26（6）：1085-1093.

［11］Yu Yueqing，Du Zhaocai，Yang Jianxin，et al.An experimental study on the dynamics of a 3-RRR flexible parallel robot［J］.IEEE Transactions on Robotics，2011，27（5）：37-46.

［12］Chang L W，Hamilton J F.The kinematics of robotic manipulators with flexible links using an equivalent rigid link system ERLS model［J］.Journal of Dynamic Systems，Measurement and Control，1991，113：48-53.

［13］Cook R D，Malkus D S，Plesha M E.Concepts and applications of finite element analysis［M］.The Unite States：Wiley，2001：75-78.

［14］Rao S S.Mechanical vibrations［M］.5th ed.Englewood Cliff：Prentice Hall，2010：431-433.