基于小波包能量的桥梁损伤识别指标*

朱劲松，孙雅舟（.夭津大学建筑工程学院 夭津，300072）（2.夭津大学滨海土木工程结构与安全教育部重点实验室 夭津，300072）

基于小波包能量的桥梁损伤识别指标*

朱劲松1，2，孙雅舟1
（1.夭津大学建筑工程学院 夭津，300072）（2.夭津大学滨海土木工程结构与安全教育部重点实验室 夭津，300072）

为达到桥梁结构损伤识别的目的，基于小波包分析方法提出了小波包能量变化率平方和（the sum square of wavelet packet energy change rate，简称WPERSS）损伤指标。分别将健康与损伤结构的加速度响应信号进行小波包分解得到小波包能量，通过计算小波包能量变化率平方和损伤指标进行损伤识别。对简支梁模型进行数值模拟，分析单一损伤与两处损伤时不同损伤程度的损伤识别情况，分析不同噪声水平对识别效果的影响。结果表明，该指标可有效识别损伤位置且对噪声具有鲁棒性。对装配式双塔斜拉桥模型进行试验，联合多个测点响应的损伤指标可以判别结构的不同损伤状态，验证了小波包能量变化率平方和指标的有效性。

小波包；损伤识别；损伤指标；能量变化率平方和

引 言

桥梁结构在使用期间由于环境等各种不利因素的影响，在结构上积累起裂缝、腐蚀和变形，造成结构局部刚度降低［1］。关键构件的损伤经过时间积累达到一定程度，将迅速扩展并导致整个结构毁坏。由于桥梁结构的健康状况直接关系到车辆行人的生命安全，因此对其损伤识别方法的研究具有重要意义。通常结构损伤识别研究可划分为4个层次［2-3］：损伤预警、损伤位置识别、损伤程度确定和结构寿命预测。前两层次是研究的前提与关键，目前研究多通过构造反应结构系统状态的损伤指标来进行损伤识别。随着小波分析方法的发展，基于小波包分析的损伤识别方法越来越得到关注。

Sun等［4-5］基于小波包分量能量方法和神经网络方法对一个二跨连续梁有限元模型进行了损伤敏感性分析。王振林等［6］提出了一种小波包组分能量变化率损伤指标，通过对简支梁的模拟分析验证了该指标对损伤预警与定位的有效性。任宜春等［7］利用小波包分解得到的特征能量向量作为损伤因子，对一根钢筋混凝土梁进行了损伤测试诊断。丁幼亮等［8-11］阐述了以小波包能量谱为基础的结构损伤预警方法的理论基础和本质，提出了能量比偏差和能量比方差两种基于动力响应的小波包能量谱损伤预警指标，并对润扬大桥悬索桥监测数据进行了小波包能量谱损伤预警分析，详细考察了不同小波函数和小波包分解层次的损伤预警效果。葛继平等［12］定义了小波包频带能量累积变异指标，利用不同激励源对一连续梁桥模型进行研究，联合多个测点小波包能量累积变异指标值可判别结构不同损伤状态。以往研究在识别损伤位置方面取得了一定成果，但对于同一损伤指标在噪声影响、损伤程度影响以及实践应用方法等方面缺乏系统深入的研究。

笔者基于小波包分析，建立了小波包能量变化率平方和损伤指标，以简支梁模型为例分析其损伤识别能力。通过装配式双塔斜拉桥模型试验，对不同损伤工况实测加速度响应进行分析，验证了所提方法的有效性。

1 小波包能量变化率平方和损伤指标

1.1 损伤指标

小波包是一系列小波基函数的组合，它具有所用小波基函数的正交性和时频特性［13］。假设小波包函数ψij，k（t），其表达式为

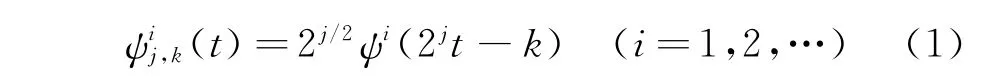
其中：i，j，k分别为小波包函数的调幅、尺度、平移参数。

小波函数ψi由如下递归关系得到

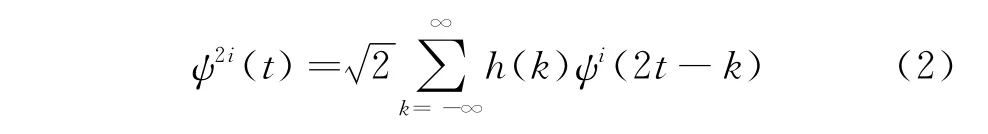
其中：h（k），g（k）分别为与尺度函数φ（t）和母小波函数ψ（t）相关的积分镜像滤波系数。

大多数母小波函数的建立需要满足一些关键特性，如可逆性和正交性。Daubechie基于膨胀方程构造了一系列母小波基函数［13］，笔者采用DB20小波进行损伤辨识。小波包分解技术可将信号分解在任意精细的频带上，在各频带形成结构响应的能量特征组从而反映结构损伤特性。文献［14］定义了小波包节点能量，且通过研究证明，利用节点能量比直接利用小波包分解系数能够得到更具有鲁棒性的信号特征。

假设对结构动力响应信号f进行第i层小波包分解得到2i个子节点，j为第i层节点编号，fi，j为第i层分解节点（i，j）上的结构响应，每个节点频带内结构响应fi，j的能量Ei，j为

则结构动力响应在第分解层的小波包能量谱向量Ei可以表征结构的动力特性

如果桥梁结构发生损伤，则其响应信号的某段频率一定会发生波动，这样按照小波包分解的各频带中某一个或某几个一定会发生能量增减，根据这些能量的增减可以判断桥梁结构的损伤。组分能量对信号特性变化是十分敏感的，它可以用来揭示信号的固有特征，定义小波包能量变化率平方和作为损伤指标对结构损伤位置进行判定。尺度i下响应小波包能量变化率平方和（WPERSS）指标为

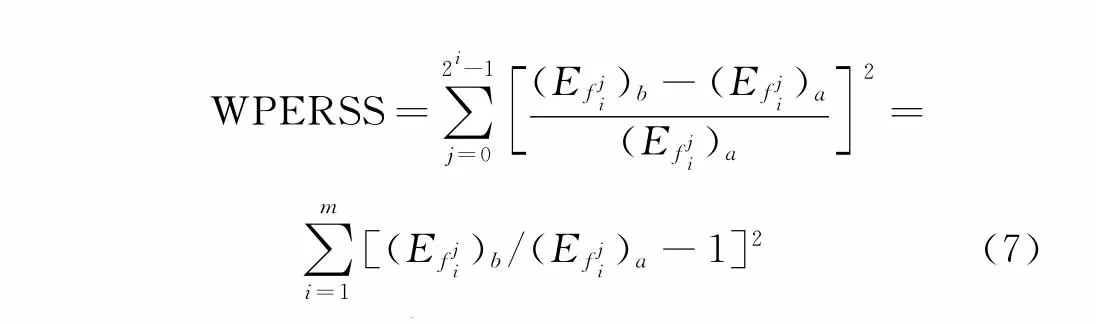
其中：（Efj

i）a为健康结构响应的信号能量；（Efj

i）b为包含损伤信息的信号能量；m=2i-1为小波包分解频带总数。

1.2 损伤识别方法

结构损伤识别是对其不同状态的比较。损伤定位过程可通过试验获得损伤结构实测加速度信号，通过建立结构理想基准模型得到健康结构响应信号，分别计算两组信号小波包节点能量，计算式（7）小波包能量变化率平方和损伤指标从而确定损伤位置，流程如图1所示。

损伤预警过程结构响应是由健康到损伤的连续信号，结构损伤使其信号发生改变从而使损伤指标发生改变。在加速度时程信号上添加滑动窗口，对相邻两滑动窗信号组计算小波包能量变化率平方和指标。若WPERSS值发生显著变化，则两组信号能量变化较大，可将两窗口时间节点作为损伤发生时刻；若未出现明显变化，说明结构前后状态未发生改变。因此，通过计算连续监测信号中WPERSS值随时间变化规律，可判断结构状态变化情况，实现损伤预警的目的。

图1 损伤位置识别流程图Fig.1 Flow chart of damage detection

2 简支梁算例分析

以图2所示的简支梁为例对结构进行模拟分析。完好状态梁高为19 cm，宽为21 cm，弹性模量为31 GPa，材料密度ρ=2 500 kg/m2。在距梁左支座1.35 m位置施加信噪比为3的随机高斯白噪声F，用来模拟环境随机激励。结构各阶模态取相同的阻尼比0.02。加速度测点布置设在图中节点1～11，即梁长的1/10位置。时程信号的采样频率为200 Hz，采样时间为10 s。

图2 简支梁模型Fig.2 Simply supported beam model

为了全面观察损伤识别效果，设定单一损伤、两处损伤等多种工况分别进行分析，如表1所示。

表1 简支梁损伤工况Tab.1 Damage cases of simply supported beam

不同损伤工况分别设定4种损伤程度（5％，10％，15％和20％）进行对比分析，单元损伤通过截面刚度下降实现。结合研究经验选取dB20小波分解加速度信号到第3尺度。以工况1为例，完好梁与10％损伤梁测点2加速度时程信号如图3所示。直接从加速度时程数据无法看出梁损伤前后的变化，采用小波包分析方法把原始信号分解为8个频带宽相同的分信号，对分解后信号运用式（5）提取各个节点的小波包能量，代入式（7）得到不同损伤程度各测点小波包能量变化率平方和指标，如图4（a）所示，由此可直观判断损伤位置。

图3 工况1完好工况与10％损伤工况测点2加速度Fig.3 Accelerate of location 2 in undamaged and 10％damaged beam

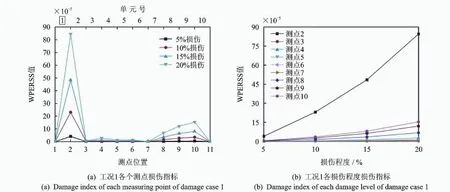
图4 工况1损伤识别效果Fig.4 Damage detection results of damage case 1

对其他工况同样应用上述方法得到各损伤情况小波包能量变化率平方和指标的识别效果。另外，为了研究WPERSS相对损伤程度的规律，取不同损伤程度下各测点WPERSS值变化规律进行分析。不同工况损伤识别效果如图4～8所示，对应损伤单元号均用方框圈出。

对于单一损伤情况，工况1损伤位于单元1时，图4（a）中测点2 WPERSS值相对于其他测点发生了显著突变，与损伤位置相符合；工况2跨中单元6损伤时，图5（a）中损伤单元两侧测点6，7损伤指标值明显大于其他测点；工况3单元10发生损伤，图6（a）中测点10的WPERSS值发生突变。各图中由于测点1，11位于支座处，竖向加速度损伤指标始终为零。对于两处损伤工况，测点损伤指标值的突变也对损伤发生位置具有指示作用。工况4单元4，10损伤图7（a）测点4，5，10损伤指标高于其他测点值，而图8（a）工况5中单元4，5损伤时测点4，5，6的指标明显突变。另外，图4（a）、图5（a）、图8（a）中测点10的损伤指标值与图6（a）、7（a）中测点2的损伤指标值也小幅突出，但均与损伤位置无关且处于支座附近。随着损伤程度增大，WPERSS值在损伤位置奇异性增强，而支座对损伤指标的干扰性也增强。图5（b）中工况1各测点损伤指标随损伤程度增大而增大，且损伤附近测点2指标远大于其他测点，而图5（b）～图8（b）中各损伤工况下损伤指标也呈现出相同变化趋势。

图5 工况2损伤识别效果Fig.5 Damage detection results of damage case 2

图6 工况3损伤识别效果Fig.6 Damage detection results of damage case 3

图7 工况4损伤识别效果Fig.7 Damage detection results of damage case 4

图8 工况5损伤识别效果Fig.8 Damage detection results of damage case 5

为测试噪声对损伤识别效果的影响，对单一损伤3种工况损伤程度10％加入高斯白噪声干扰研究，噪声水平分别取2％，3％和5％。各噪声水平下分别施加20组不同的白噪声进行损伤识别，取损伤指标的平均值表示该噪声水平下的损伤识别结果，如见图9所示。

由图9（a），（b）可见，在选取不同噪声水平下，单元1，6的损伤指标规律与无噪声状态相同，且随着噪声水平增加，损伤指标在损伤位置奇异性增强。图9（c）中单元10在噪声达到5％时与其他噪声情况出现差异，非损伤单元测点的损伤指标也发生变化，说明噪声产生了一定干扰效果，但根据损伤指标峰值仍可大致识别损伤位置。

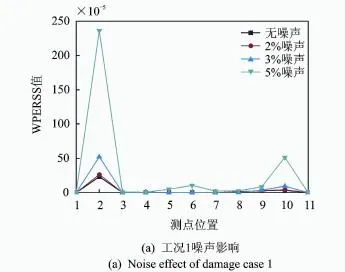
图9 各工况损伤10％情况噪声影响Fig.9 Noise effect of different damage cases with 10％rigidity reduced

3 斜拉桥模型试验验证

对装配式双塔斜拉桥模型进行试验，模型总体布置如图10所示。斜拉桥共二跨，总长为7.8 m，主跨长为4.2 m，两边跨各为1.8 m，索塔高为1.52 m。在主跨跨中处、主跨1/4处、两侧支座附近位置分别安装加速度传感器（1#～5#）。设置3种损伤工况：工况1主跨跨中主梁截面刚度下降10％；工况2边跨跨中主梁截面刚度下降10％；工况3去除索塔A处橡胶支座。主梁截面刚度下降通过更换桥面板实现。采用冲击力激励获得自由振动响应模拟环境激励响应，加速度信号采样频率为125 Hz，各损伤工况与完好工况分别测得8组信号，采用DB20小波4层分解进行小波包分析，计算得到WPERSS值从而得到损伤识别结果，如图11～13所示。

图10 斜拉桥模型总体布置（单位：mm）Fig.10 Layout of cable-stayed bridge model（unit：mm）

图11 主跨跨中损伤10％识别效果Fig.11 Damage detection results with 10％rigidity reduced at the middle of main span

图12 边跨跨中损伤10％识别效果Fig.12 Damage detection results with 10％rigidity reduced at the middle of side span

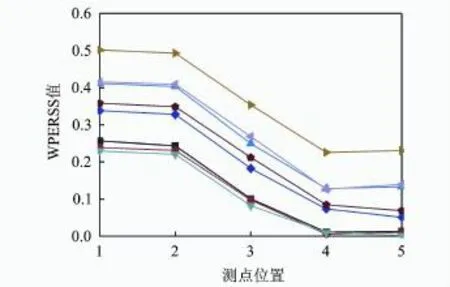
图13 去除索塔A支座损伤识别效果Fig.13 Damage detection results without rubber support at tower A

虽然图12～13中各组损伤指标受所取信号长度不同而数值不同，但结果均显示出相同规律。工况1各组结果中位于主跨跨中的测点3损伤指标值均相对于其他测点明显突出，指示跨中位置存在损伤；工况2各组损伤指标由测点1到测点5呈现出依次递减趋势，表明损伤位置距测点1更近，与边跨跨中损伤工况相符；工况3中测点1、测点2相对于其他二测点均明显突出，损伤位置索塔A位于两测点之间。

变化率平方和指标是一种简单易行的损伤识别指标，仅需不同损伤状态下多个测点的加速度响应时程计算该指标值。不同信号长度的加速度数据对损伤指标数值有影响，但相同损伤情况各测点指标的规律性基本一致，均可反映损伤发生位置。

4 结 论

1）对简支梁模型进行仿真模拟的结果表明，小波包能量变化率平方和指标对不同损伤程度的单一损伤与两处损伤均可有效识别。不同水平白噪声信号与无噪信号的识别结果对比，验证了损伤指标对噪声具有鲁棒性。通过斜拉桥模型损伤试验，对健康工况与3种损伤工况的加速度信号进行采集，联合多测点的结果分析，验证了损伤指标对损伤位置可有效识别。

2）在简支梁算例中，不同损伤工况下小波包能量变化率平方和指标随损伤程度的增加呈现将滑动窗口与笔者提出的损伤指标相结合为桥梁结构损伤预警的实现提供了一条新的思路。

［1］ 曾欣，徐兆东.基于应变能量分布变化的大跨桥损伤识别［J］.振动、测试与诊断，2012，32（2）：267-270.Zeng Xin，Xun Zhaodong.Damage detection strategy for long-span bridge based on strain energy distribution change［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（2）：267-270.（in Chinese）

［2］ Rytter A.Vibration-based inspection of civil engineering structures［D］.Aalborg：University of Aalborg，1993.

［3］ Doebling S W，Farrar C R，Prime M B.A summary review of vibration-based damage identification methods［J］.Shock＆amp；Vibration Digest，1998，30（2）：91-105.

［4］ Sun Z，Chang C C.Structural damage assessment based on wavelet packet transform［J］.Journal of Structural Engineering，2002，128（10）：1354-1361.

［5］ Sun Z，Chang C C.Statistical wavelet based method for structural health monitoring［J］.Journal of Structural Engineering，2004，130（7）：1055-1062.

［6］ 王振林，聂国华.曲率模态和小波包变换在结构损伤识别中的应用［J］.振动与冲击，2008，27（1）：124-126.Wang Zhenlin，Nie Guohua.A method for structure damage detection based on curvature mode and wavelet packet transformation［J］.Journal of Vibration and Shock，2008，27（1）：124-126.（in Chinese）

［7］ 任宜春，张杰峰，刘哲峰.钢筋混凝土梁损伤的小波包识别方法［J］.振动、测试与诊断，2011，31（5）：605-609.Ren Yichun，Zhang Jiefeng，Liu Zhefeng.Damage identification of reinforced concrete beam based on wavelet packet［J］.Journal of Vibration，Measurement ＆amp；Diagnosis，2011，31（5）：605-609.（in Chinese）

［8］ 丁幼亮，李爱群，缪长青.基于小波包能量谱的结构损伤预警方法研究［J］.工程力学，2006，23（8）：42-48.Ding Youliang，Li Aiqun，Miao Changqing.Investigation on the structural damage alarming method based on wavelet packet energy spectrum［J］.Engineering Mechanics，2006，23（8）：42-48.（in Chinese）

［9］ 丁幼亮，李爱群，缪长青.环境激励下基于小波包分析的结构损伤预警方法研究［J］.应用力学学报，2008，25（3）：366-370.Ding Youliang，Li Aiqun，Miao Changqing.Structural damage alarming method based on wavelet packet analysis by ambient vibration test［J］.Chinese Journal of Applied Mechanics，2008，25（3）：366-370.（in Chinese）

［10］丁幼亮，李爱群，邓扬.面向结构损伤预警的小波包能量谱识别参数［J］.东南大学学报：自然科学版，2011，41（4）：824-828.Ding Youliang，Li Aiqun，Deng Yang.Parameters for identification of wavelet packet energy spectrum for structural damage alarming［J］.Journal of Southeast University：Natural Science Edition，2011，41（4）：824-828.（in Chinese）

［11］Ding Youliang，Li Aiqun，Liu Tao.A study on the WPT-based structural damage alarming of the ASCE benchmark experiments［J］.Advances in Structural Engineering，2008，11（1）：121-127.

［12］葛继平，李胡生.基于小波包能量累积变异的梁桥损伤识别试验［J］.振动、测试与诊断，2011，31（1）：85-88.Ge Jiping，Li Husheng.Experiment on damage detection of girder bridge using wavelet packet energy accumulated variation［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2011，31（1）：85-88.（in Chinese）

［13］郭健，陈勇，孙炳楠.桥梁健康监测中损伤特征提取的小波包方法［J］.浙江大学学报：工学版，2006，40（10）：1767-1772.Guo Jian，Chen Yong，Sun Bingnan.Wavelet packet method of damage feature extraction in bridge health monitoring［J］.Journal of Zhejiang University：Engineering Science，2006，40（10）：1767-1772.（in Chinese）

［14］Yen G G，Lin K C.Wavelet packet feature extraction for vibration monitoring［J］.IEEE Transactions on Industrial Electronics，2000，47（3）：650-667.

TU311.41；U445.7；TH165.3

10.16450/j.cnki.issn.1004-6801.2015.04.019

朱劲松，男，1975年10月生，教授。主要研究方向为桥梁损伤识别与健康监测。曾发表《Bridge-vehicle coupled vibration response and static test data based damage identification of highway bridges》（《Structural Engineering and Mechanics》2013，Vol.46，No.1）等论文。

E-mail：jszhu@tju.edu.cn

*夭津市应用基础与前沿研究计划资助项目（14JCYBJC21500）；国家自然科学基金资助项目（51178305）

2013-08-18；

2013-11-03