基于ICA相关系数和VPMCD的滚动轴承故障诊断*

2015-01-12程军圣马兴伟湖南大学汽车车身先进设计制造国家重点实验室长沙410082

振动、测试与诊断 2015年4期

程军圣，马兴伟，杨宇（湖南大学汽车车身先进设计制造国家重点实验室长沙，410082）

程军圣，马兴伟，杨宇
（湖南大学汽车车身先进设计制造国家重点实验室长沙，410082）

将基于变量预测模型的模式识别（variable predictive model based class discriminate，简称VPMCD）、独立分量分析（independent component analysis，简称ICA）和相关系数分析方法相结合，提出了基于ICA相关系数和VPMCD的滚动轴承故障诊断方法。首先，对不同工况下的滚动轴承振动信号分别进行独立分量分析，获得各工况信号的独立分量；然后，提取样本与不同工况信号独立分量之间的相关系数，并以相关系数绝对值的和作为该样本的特征值；最后，采用VPMCD分类器进行故障识别和分类。实验数据的分析结果表明，该方法能够有效应用于滚动轴承故障诊断。

变量预测模型的模式识别；独立分量分析；相关系数；滚动轴承；故障诊断

引言

机械故障诊断过程本质上是一个故障模式识别的过程［1］，针对某一具体的机械故障诊断问题，选择不同的模式识别方法，其分类精度和准确性可能会有较大的差异［2-3］。神经网络结构和类型的选择过分依赖于先验知识或经验，将会影响其分类精度［4］。支持向量机分类结果受核函数及其参数的影响，其搜索算法本质上是二进制的，对于多类分类问题需要进行多次的二进分类［5］。

文献［6-8］提出的VPMCD方法利用从原始数据中提取的特征值之间的相互内在关系建立数学模型，可以应用于多变量描述的非线性系统的模式识别问题。由于在机械故障诊断中，所有或部分特征值之间具有一定的相互内在关系，因此VPMCD方法可以应用于机械故障诊断。

独立分量分析［9］是一种基于高阶统计特性的无监督特征提取方法，其基本思想是假定样本集是由一组相互独立的基向量和相应的混合矩阵相乘构成，利用相应的算法求出混合矩阵的逆矩阵。目前，基于ICA的机械故障诊断方法需要多个通道信号进行独立分量提取或者需要知道机械故障的特征频率，使ICA的应用受到限制。Kotani等［10］利用ICA直接从原始手写数字图像中提取特征信息，发现ICA能够有效提取图像的内在结构特征。赵志宏等［11］利用ICA直接从原始机械振动信号中提取机械故障的独立分量，发现ICA能够有效提取机械故障的特征信息。从机械故障振动信号中提取到的独立分量蕴含了一些机械故障的特征信息，不同工况的机械振动信号提取的独立分量与该工况信号的相关程度较高，而与其他工况的振动信号相关程度较低，因此独立分量分析和相关系数可以用作机械故障诊断的特征参数。为反映总体的相关程度，避免少数异常情况的影响，笔者采用样本与不同工况振动信号提取的独立分量相关系数绝对值的和作为故障特征。

笔者将ICA相关系数和VPMCD方法相结合用于滚动轴承故障诊断，利用ICA直接从原始振动信号中获取独立分量特征信息，用样本与独立分量相关系数绝对值的和作为特征值，采用VPMCD方法进行模式识别。将VPMCD方法与支持向量机（support vector machine，简称SVM）进行实验对比分析，结果表明，VPMCD方法可以更有效地应用于滚动轴承故障诊断。

1 基于ICA相关系数和VPMCD的滚动轴承故障诊断步骤

ICA是一种从多个独立的信号叠加而成的混合其中：Cov（X，Y）为变量X和Y的协方差；D（X），D（Y）分别为变量X和Y的方差。

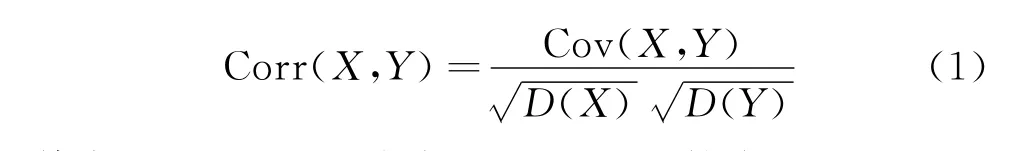
相关系数的取值范围为［-1，1］，相关系数的绝对值越大，说明两个变量的线性相关程度越高。

基于ICA相关系数和VPMCD的故障诊断方法具体步骤如下。

1）假设有n种不同工况的样本集，分别记为Condition1，Condition2，…，Con ditionn。对于第i种工况的训练样本集，采用ICA方法提取m个独立分量并将独立分量组成的集合记为ICAi。n种不同工况的样本集共得到n个独立分量集合。

2）从训练样本集中任取一个训练样本记为S-train，计算训练样本S-train与ICAi（i=1，2，…，n）中各个独立分量的相关系数绝对值的和。训练样本S-train共得到n个特征值featurei（i=1，2，…，n），这n个特征值组成样本S-train的特征值向量。

3）将训练样本集的特征值向量输入到VPMCD分类器，VPMCD利用训练样本估计模型参数，建立变量预测模型。

4）采用与训练样本相同的方法计算测试样本的特征值向量，利用VPMCD进行识别，从而确定测试样本的故障类型。信号中提取单个源信号的方法。ICA的模型定义可参考文献［12］。在众多ICA算法中，特征矩阵联合近似对角化方法（joint approximate diagonalization of eigen-matrices，简称JADE）［13］是一种批处理算法，适合处理一批已经取得的数据。该算法的主要特点是引入了多变量数据的四阶累积量矩阵，简化了算法，提高了结果的稳定性。

相关系数是描述变量之间相关程度的指标。假设两个变量X和Y，两者的相关系数为

2 实验分析

机械设备在运行时，其关键零部件滚动轴承可能会出现内圈故障、外圈故障、滚动体故障或保持架故障。为验证ICA相关系数和VPMCD方法的有效性，采用美国凯斯西储大学电气工程实验室的滚动轴承数据［14］，选用的滚动轴承为6205-2RS JEM SKF型深沟球轴承，滚动轴承的损伤状况为单一损伤。笔者对采样频率为12 k Hz、电机负载为0 HP、转速为1 797 r/min的不同损伤程度的10组数据进行了9种不同的故障诊断测试。图1为某一组滚动轴承故障振动加速度信号。

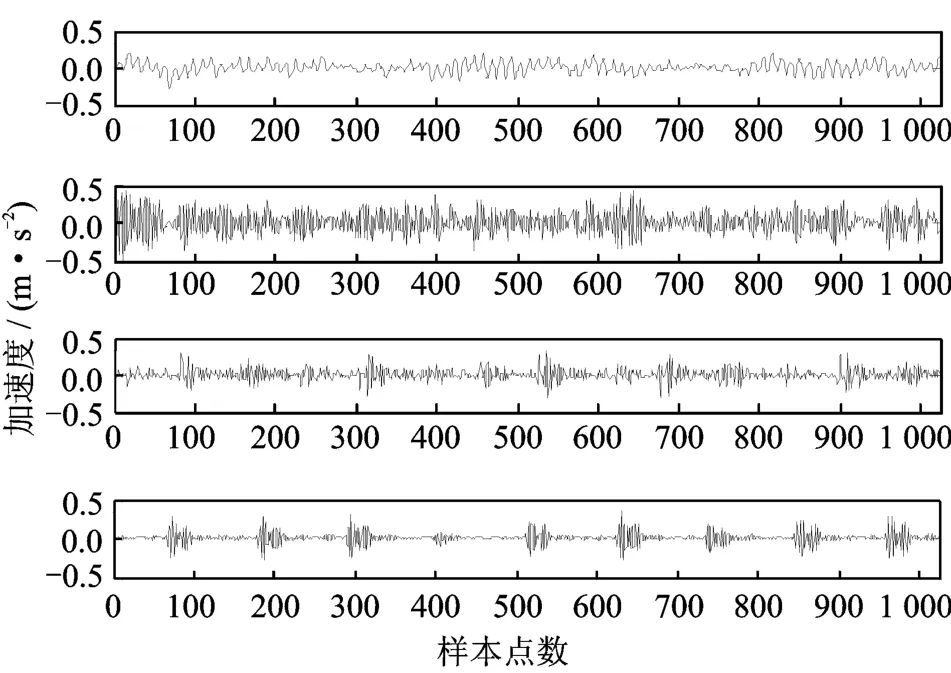
图1 滚动轴承4种工况下的振动加速度信号Fig.1 Vibration acceleration signal of four rolling bear conditions

实验中数据集的选择如表1所示，每个样本集的采样点数为1 024。数据集名称中的字母N和3组数字分别代表滚动轴承4种状态对应的故障直径的大小（N，07，14，21分别对应故障点的直径为0，0.177 8，0.355 6和0.533 4 mm）。例如，N-07-07-07数据集，N代表正常，07-07-07代表滚动体（B）、内圈（I）、外圈（O）的故障直径都为0.177 8 mm。NBall，N-Inner，N-Outer 3种数据集分别包含了滚动体故障、内圈故障和外圈故障3种故障程度的数据。

表1 实验数据集Tab.1 The experimental data set

首先，利用ICA相关系数法提取滚动轴承故障特征。对于数据集N-07-07-07，N-14-14-14，N-21-21-21，N-07-14-21，N-21-07-14，N-14-21-07中的每个训练样本均可得到4个特征值。feature1，feature2，feature3，feature4分别为训练样本与正常信号独立分量、滚动体故障独立分量、内圈故障独立分量和外圈故障独立分量的相关系数绝对值求和得到。对于数据集N-Ball，N-Inner，N-Outer中的每个训练样本可得到4个特征值。feature1，feature2，feature3，feature4分别为训练样本与相应数据集中各个故障独立分量的相关系数绝对值求和得到。对于测试样本采用与训练样本相同的方法计算其特征值向量。其次，对于每一种数据集，将数据集中滚动轴承4种工况的训练样本分别输入到VPMCD分类器中对其进行训练，再将测试样本输入到VPMCD分类器中进行模式识别。

笔者以数据集N-07-07-07为例，将滚动轴承正常测试样本集得到的独立分量记为ICA1。ICA1与某一组滚动轴承正常、滚动体故障、内圈故障、外圈故障的测试样本的相关系数如表2所示。由表2可知，ICA1与滚动轴承正常样本的相关程度较高，与滚动轴承其他3类故障样本的相关程度较低。正常2测试样本与ICA1相关程度较低，直接利用相关系数作为特征值并不理想。利用滚动轴承测试样本与ICA1相关系数绝对值的和作为故障特征值，一方面能有效反映测试样本总体的相关程度，另一方面也避免了少数异常情况的干扰。因此，笔者采用滚动轴承样本与相应样本集的独立分量的相关系数绝对值的和作为特征。

表2 滚动轴承正常测试样本集独立分量与测试样本集的相关系数Tab.2 The correlation coefficients between the independent components of the normal rolling bear test sample and the test samples

表3 基于VPMCD的滚动轴承故障识别结果Tab.3 Results of pattern recognition based on VPMCD

故障1为滚动体故障；故障2为内圈故障；故障3为外圈故障

VPMCD方法利用训练样本估计模型参数，建立变量预测模型VPMk（k=1，2，3，4时，分别对应为正常、滚动体故障、内圈故障、外圈故障样本的预测模型），从而对测试样本的故障类型分类。表3为表2中滚动轴承测试样本的VPMCD测试诊断结果。表4为基于ICA相关系数和VPMCD滚动轴承故障诊断方法对美国凯斯西储大学电气工程实验室的滚动轴承不同损伤程度的10组数据、9种不同故障诊断测试结果。为进一步说明VPMCD方法的优越性，笔者采用ICA相关系数和SVM对以上不同损伤程度的10组数据、9种不同的故障进行诊断测试，如表5所示。

由表4和表5可知，VPMCD和SVM分类器对于9种不同的故障均达到较高的识别率，说明了ICA相关系数特征提取方法的有效性和鲁棒性。另外，SVM需要进行严格的结构参数优化选择才能达到较高的识别率，而VPMCD分类器无需进行任何结构参数的优化选择，且对于不同的故障类型都能达到较高的识别率。综合上述实验分析，显然VPMCD方法更适用于滚动轴承故障诊断。

表4 基于ICA相关系数和VPMCD的滚动轴承故障识别结果Tab.4 Results of pattern recognition based on correlation coefficient of independent component analysis and VPMCD

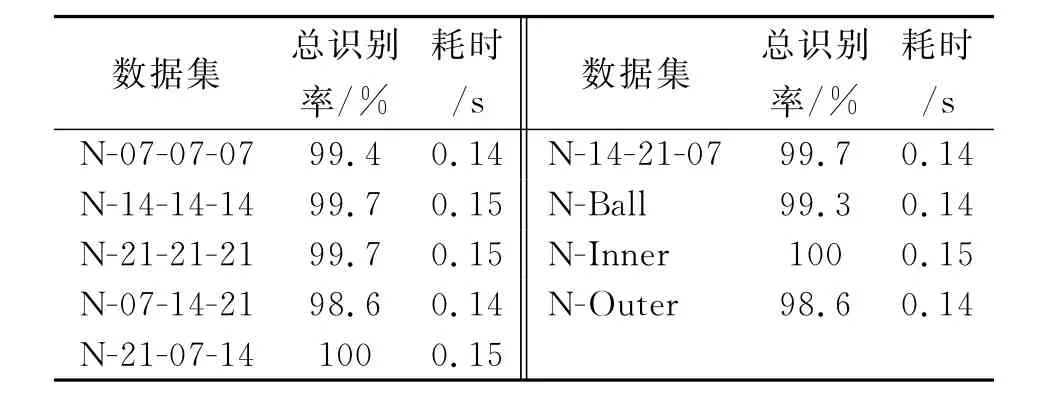
表5 基于ICA相关系数和SVM的滚动轴承故障诊断结果Tab.5 Results of pattern recognition based on correlation coefficient of independent component analysis and SVM

3 结论

1）从原始数据中提取的特征值实际上反映了原始数据的本质特征，VPMCD方法依据特征值之间的相互内在关系建立预测模型，采用预测模型对测试样本进行分类，无需任何结构参数的选择，能更有效地实现分类。

2）利用样本与不同工况滚动轴承振动信号提取的独立分量的相关系数绝对值的和作为样本故障特征值，反映了样本总体的相关程度，有效提取出滚动轴承故障特征信息。

3）将ICA相关系数和VPMCD方法引入滚动轴承故障诊断中，通过对滚动轴承9种不同的故障诊断测试以及与SVM实验对比分析，表明了ICA相关系数和VPMCD方法可以更有效地对多种故障特征进行模式识别。

［1］温熙森.模式识别与状态监控［M］.北京：科学出版社，2007：1-5.

［2］ Lei Yaguo，He Zhengjia，Zi Yanyang，et al.New clustering algorithm-based fault diagnosis using compensation distance evaluation technique［J］.Mechanical Systems and Signal Processing，2008，22（2）：419-435.

［3］ Rafiee J，Tse P W，Harifi A，et al.A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system［J］.Expert System with Applications，2009，36（3）：4862-4875.

［4］ Wang Chun-Chieh，Kang Yuan，Shen Pingchen，et al.Applications of fault diagnosis in rotating machinery by using time series analysis with neural network［J］.Expert System with Application，2010，37（2）：1696-1702.

［5］ Fei Shengwei，Zhang Xiaobin.Fault diagnosis of power transformer based on support vector machine with genetic algorithm［J］.Expert Systems with Application，2009，36（8）：11352-11357.

［6］ Raghuraj R，Lakshminarayanan S.Variable predictive models-a new multivariate classification approach for pattern recognition applications［J］.Pattern Recognition，2009，42：7-16.

［7］ Raghuraj R，Lakshminarayanan S.Variable predictive model based classification algorithm for effective separation of protein structural classes［J］.Computational Biology and Chemistry，2008，32（4）：302-306.

［8］ Raghuraj R，Lakshminarayanan S.VPMCD：variable interaction modeling approach for class discrimination in biological system［J］.Federation of European Biochemical Societies Letter，2007，581（5-6）：826-830.

［9］ Hyvarinen A，Karhunen J，Oja E.Independent component analysis［M］.New York：John Wiley，2001：10-80.

［10］Kotani M，Ozawa S.Feature extraction using independent components of each category［J］.Neural Processing Letters，2005，22（2）：113-124.

［11］赵志宏，杨绍普，申永军.基于独立分量分析与相关系数的机械故障特征提取［J］.振动与冲击，2013，32（6）：67-71.Zhao Zhihong，Yang Shaopu，Shen Yongjun.Machinery fault feature extraction based on independent component analysis and correlation coefficient［J］.Journal of Vibration and Shock，2013，32（6）：67-71.（in Chinese）

［12］黄晋英，毕世华，潘宏侠，等.独立分量分析在齿轮箱故障诊断中的应用［J］.振动、测试与诊断，2008，28（2）：126-130.Huang Jinying，Bi Shihua，Pan Hongxia，et al.Fault diagnosis for gears based on independent component analysis［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2008，28（2）：126-130.（in Chinese）

［13］Cardoso J F，Souloumiac A.Blind beamforming for non-Gaussian signals［J］.IEEE Proceedings F，1993，140（6）：362-370.

［14］Case Western Reserve University Bearing Data Center.Bearing data center fault test data［EB/OL］.［2012-11-10］.http：//www.eecs.case.edu/laboratory/bearing.