AMT平顺起步的优化控制*

王斌陈勇郭立书李雪松高炳钊陈虹，3

（1.吉林大学 汽车仿真与控制国家重点实验室；2.吉利汽车研究院；3.吉林大学）

AMT平顺起步的优化控制*

王斌1陈勇2郭立书2李雪松1高炳钊1陈虹1，3

（1.吉林大学 汽车仿真与控制国家重点实验室；2.吉利汽车研究院；3.吉林大学）

当离合器摩擦片的摩擦系数、车身质量及道路坡度等参数发生较大变化时，会使线性二次型优化控制算法改善AMT车辆起步平顺性的效果下降。设计了一种考虑模型误差估计的优化控制算法，即通过一个降维误差观测器对时变的参数和模型的不确定性进行估计，并由估计的模型误差和车辆状态共同构成控制算法的线性反馈。通过实车试验对该算法进行验证，结果表明在车辆参数变化时该算法可以保证AMT车辆平顺起步。

1 前言

AMT是在机械式手动变速器基础上安装自动控制机构以实现离合器和换挡自动化的一种自动变速器，其具有传动效率高、结构简单、制造成本低、可靠性强、适应环境能力、易加工等优点[1，2]。由于干式离

5 Mäder K M.Continuously Variable Transmission:Bench⁃mark,Status&Potentials,2005:1～30.

6 Bonsen B,Steinbuch M,Veenhuizen P.CVT ratio control strategy optimization.IEEE Vehicle Power and Propulsion Conference,2005:227～231.

7 Hofman T,Steinbuch M,etal.Design of CVT-Based Hybrid Passenger Cars.IEEE Transactions on Vehicular Technolo⁃ gy,2009,58（2）：572～587.

8 OAK RIDGE NATIONAL LABORATORY.PHEV Value Proposition Study Final Report 2010:218.

9 Lu S.Vehicle Survivability and Travel Mileage Schedules.Security,2006:40.

（责任编辑晨 曦）

修改稿收到日期为2015年2月1日。合器的存在，AMT车辆普遍存在起步冲击大的缺点。车辆起步过程的快速响应及减小离合器滑磨的要求与减小冲击、平顺起步相矛盾，而且驾驶员意图无法预测、车辆的行驶工况复杂都给车辆平顺起步控制带来困难[3]。

目前的发动机恒转速算法[4]无法避免离合器闭合瞬间的起步冲击，也无法显示考虑滑磨功与冲击度的矛盾。文献[5]中将基于LQR的优化控制算法应用到了离合器起步控制过程，该控制策略的目标函数中考虑了离合器的快速结合和减小冲击两个关键因素，因此车辆在快速起步的同时能够保证平顺性。但是，车辆行驶工况的复杂性也会影响其起步特性，例如离合器摩擦片温度、车辆质量、行驶路况等参数的变化都会影响车辆的起步平顺性。因此，本文设计了模型误差观测器，对这些时变参数和模型误差进行统一估计，并将此估计误差与车辆的状态同时作为线性反馈，搭建车辆传动系统的控制模型，构建基于LQR的AMT车辆起步优化控制算法。并且对一辆中型轿车进行改造，搭建实车试验平台，对该算法进行实车验证，并与不考虑模型误差的优化算法进行比较。

2 控制问题描述

2.1 传动系统模型

对某配备AMT的中型轿车传动系统进行建模，该传动系统包括干式离合器和五挡机械式变速器。在车辆起步时该传动系统可以简化为如图1所示的二质量系统，其动力学方程为：

式中，ωe是发动机转速；ωc是离合器转速；Te是发动机输出扭矩；Tc是离合器摩擦扭矩；Tl是汽车行驶阻力矩；Ce和Cv是发动机、传动系统的阻尼系数；Ie和Iv分别是发动机、传动系统的等价转动惯量。

将离合器摩擦扭矩的导数作为控制输入u，这样传动系统振动和车辆冲击就被考虑到了控制器中，因此通过对u的合理控制可以减轻传动系统和车辆的冲击，从而改善车辆的起步平顺性。

2.2 控制问题描述

由于离合器摩擦片的摩擦因数随温度而变化，模型中离合器摩擦扭矩的值会出现计算误差。离合器有效摩擦半径、车辆质量、道路坡度等参数和工况的变化都带来模型误差。模型误差统一由w=[w1，w2]表示，并且可以通过下面的观测器进行估计：

式中，Δω=ωe-ωc。

为了同时使传动系统的振动和摩擦损失最小，目标函数设计为：

其中，qΔω、qfriction和r是惩罚因数，通过分析可以得到以下结论：

a.qΔωΔω2可以促使离合器的相对滑磨速度减小到0，从而保证离合器的接合时间最短；

bqfrictionTcΔω可以使摩擦损失最小；

crT˙c保证车辆平顺起步。因为Tc决定车辆的加速度，所以车辆的冲击度可以由T˙c来表示。

3 考虑模型误差的优化控制器设计

3.1 模型误差观测器设计

选择x0=[ωe，∆ω]T，u0=[Tc，Te，Tl]T分别作为状态变量和输入变量，并且定义w=[w1，w2]T，则公式（4）和公式（5）用状态空间描述为：

其中，L∈R2×2是观测器增益，是待设计的常量。为了避免wˆ的微分，可以令

对式（10）进行微分得：

进一步得：

公式(10)和公式（12）构成了AMT车辆传动系统的降维观测器。

定义观测器误差为：

对该误差的动力学意义可以进行以下描述：

假设模型误差是缓变的，则式（14）可以改写为：

即可以通过选择合适的L∈R2×2来保证估计误差是收敛的。

3.2 控制器设计

结合模型误差观测器（10）、（12）和原始的状态空间方程（7），可以得到一个增广的系统，该增广系统的状态是：

其中，增加的状态向量Tc是为了在惩罚方程中表示摩擦损失和起步冲击。

由于Te和Tv分别随着驾驶员对油门踏板的操作和道路坡度变化而改变，是可以测量但无法预测的，因此将其和模型误差共同作为系统的扰动，即

系统的输入是：

则带有模型误差观测器的增广动力学系统可以表示为：

因此，控制问题变成了对目标函数的最小化问题：

式中，Q∈R3×3和R∈R1×1是加权矩阵，其分别为

其中，q11和q33是较小的值。虽然这是一个无限的时域优化控制问题，但是由于对xTQx项的惩罚保证了离合器的完全接合。

应用汉密尔顿方法[6]，选择汉密尔顿函数方程：

其中，λ是待定的因数，进而该最优方案就符合以下微分方程形式：

以及

定义λ为：

其中，P∈R3×3和h∈R3×4是待定的定常矩阵，P由解下面的黎卡提方程得到：

而h由下式决定：

最终得到控制律：

详细的推导过程请参考文献[7]。上述方程可以离线计算，而在线的控制律可以改写为：

根据试验车的相关参数进行控制器设计，其参数如表1所列。

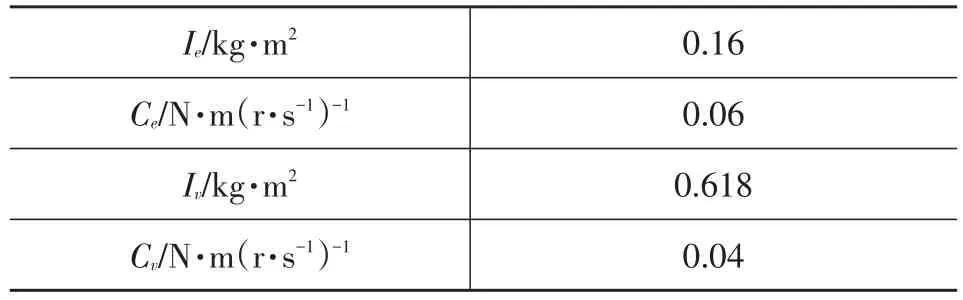
表1 试验轿车参数

通过试验对权重矩阵Q和R进行调节，得到Q和R的值：

则控制器增益为：

该优化控制器利用了ωe、Δω、Tc、Te、Tl以及模型误差w1、w2的反馈。通过Δω=ωe-ωc和方程（31），控制器可以写为：

ωe、Te以及ωc可以通过CAN总线得到，Tc和Tl可以通过离合器位置传感器和道路坡度传感器近似计算得到。实际控制的Tc是通过对u=T˙C计算得到的，并施加在系统上。

4 实车试验

对一辆国产中型轿车进行改装，安装离合器电动执行机构，实现离合器的自动化。利用DSPACE工具作为仿真控制器，与车辆进行通信并实现车辆自动起步。控制器的采样时间设定为10 ms。

不考虑模型误差估计的优化控制算法可以使AMT车辆在参数不变和行驶工况固定的情况下平稳起步，但是在实际行驶过程中，车辆参数及行驶工况是不断变化的。当试验车的质量和道路坡度同时发生变化时，如试验车的质量由1 500 kg增至1 800 kg、道路坡度由0增至8.7%时，没有观测器和带有观测器的优化算法试验结果如图2和图3所示。可知，不考虑模型误差估计的优化算法已经无法使车辆平顺起步，在离合器结合过程中，发动机和离合器输出转速抖动剧烈，同时发动机扭矩也产生波动，造成汽车的起步平顺性很差；而考虑模型误差估计的优化算法可以使车辆平顺起步，从踩油门踏板到离合器完全接合完成起步用了约2 s的时间，同时发动机和离合器输出端转速变化平稳，起步平顺。

因此，带有观测器的优化控制算法可以对模型误差进行观测，可以适应车辆参数或行驶工况的变化，可以满足汽车在各种工况下的平顺起步要求。

5 结束语

基于LQR的优化控制算法可以很好的解决AMT车辆的多目标控制问题，实现车辆的平顺起步。但是由于汽车参数和行驶工况变化所产生的模型误差会降低优化控制算法的控制效果，甚至会导致起步失败。本文提出的带有模型误差观测的优化控制算法可以对模型误差进行估计，从而使车辆对参数和行驶工况的变化有了自适应性能。通过实车试验证实了本算法可以在行驶工况发生较大变化后保持车辆的平顺起步性能。

1 李君，张建武，冯金芝，等.电控机械式自动变速器的发展、现状和展望.汽车技术,2000（3）：1～3.

2 Dolcini P，Wit C C，Bechart H.Lurch avoidance strategy and its implementation in AMT vehicles.Mechatronics，2008，18:289～300.

3 Lei Y，Niu M，Ge A.A research on starting control strate⁃gy of vehicle with AMT.FISITA World Automotive Con⁃gress Seoul，Korea，2000.

4 雷雨龙，葛安林，李永军．离合器起步过程的控制策略．汽车工程，2000，22（4）:266～269.

5 唐娜娜，陈勇，高阳，等.6-AMT微型乘用车起步优化控制.汽车技术，2014（4）:21～24.

6 Bryson A，Ho Y.Applied Optimal Control.Washington DC: Hemisphere，1981.

7 Gao B Z，Chen H，Lu X T，etal.An improved optimal controller for start-up of AMT trucks in consideration of driver’s intention.International Journal of Automotive Tech⁃nology，2013，14:213～220.

（责任编辑晨 曦）

修改稿收到日期为2015年2月1日。

Optimal Control for the Smooth Launch of AMT

Wang Bin1,Chen Yong2,Guo Lishu2;Li Xuesong1,Gao Bingzhao1,Chen Hong1,3
（1.State Key Laboratory of Automotive Simulation and Control,Jilin University; 2.Geely Automobile Research Institute;3.Jilin University）

When parameters like clutch friction coefficient,vehicle mass and road slope vary greatly,the linearquadratic based optimal control algorithm can improve the smooth launch control performance of AMT.An optimal launch control algorithm considering modeling error estimation is designed,which uses a reduced-order observer to estimate the time-varying parameters and uncertainty of model,and constitute a linear feedback of the control algorithm with the estimated model errors and vehicle state.The proposed control algorithm is verified in real vehicle test which proves that the proposed control algorithm can ensure the vehicle to launch smoothly when vehicle parameters change.

AMT,Smooth launch,Modeling error estimation,Control algorithm

AMT 平顺起步 模型误差估计 控制算法

U463.2

A

1000-3703（2015）06-0006-04

国家自然科学基金（61374046）、吉林省科技厅重点攻关项目（20150204056GX）、吉林省科技厅青年基金（20130522183JH）资助。