基于微分变分原理研究相空间中非完整系统的守恒律

翟相华，张毅

(1.苏州科技学院 数理学院，215009;2.苏州科技学院 土木工程学院， 215011)

0 引言

寻找力学系统的守恒律一直是数学物理学科特别是分析力学的一个重要研究方向.Newton 力学建立了三个经典守恒律，Lagrange 力学和Hamilton 力学给出了循环积分和广义能量积分，对称性方法得到了更多的守恒律，如Noether 守恒量，Hojman 守恒量，Mei 守恒量等［1－7］.基于微分变分原理也可以直接构造系统的守恒律［7］.刘端［8］应用Jourdain 微分变分原理研究了非完整非保守力学系统的守恒律，梅凤翔［9］研究二阶非完整系统的守恒律，张毅［10］利用微分变分原理研究了单面约束系统的守恒律，李元成等［11］将结果推广到事件空间中.但是笔者至今尚未见到利用微分变分原理研究相空间中力学系统守恒律的文献.本文首先导出相空间中非完整非保守力学系统的微分变分原理，进而建立其在无限小变换下的不变性条件，进一步导出了相空间中非完整非保守系统的守恒律.结果表明利用微分变分原理也可以研究相空间中力学系统的守恒律.

1 相空间中非完整力学系统的微分变分原理

假设力学系统的位形由n 个广义坐标qs(s=1，…，n)来确定，其运动受有g 个双面理想Chetaev 型非完整约束

按约束加在虚位移上的Appell－Chetaev 定义，有

系统的运动微分方程为

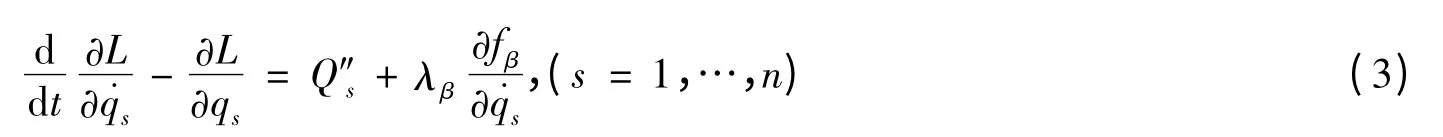
其中L 为Lagrange 函数，Q″s为非势广义力，λβ为约束乘子.设系统非奇异，则可在运动微分方程积分之前，解出约束乘子λβ作为的函数.

令

于是方程(3)可表为

称方程(5)为与非完整系统(1)，(3)相应的完整系统的方程.

引进广义动量和Hamilton 函数

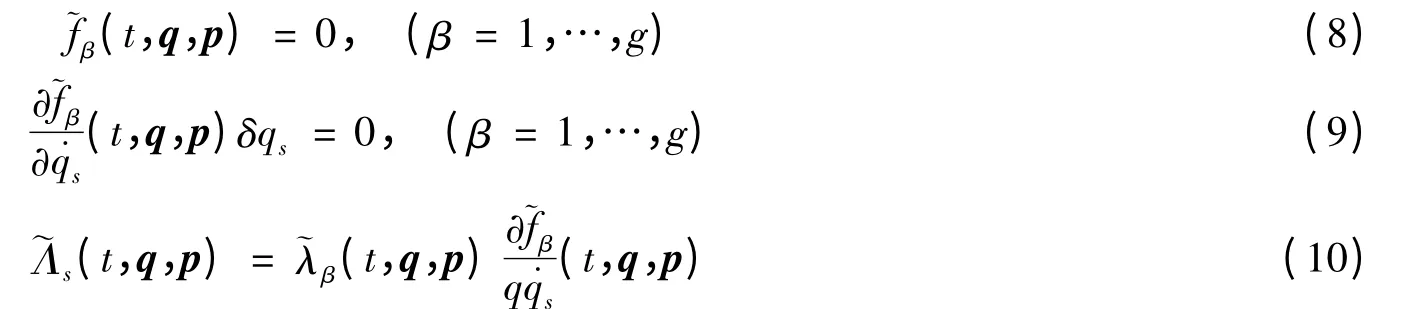
非保守系统的Hamilton 原理为［3－4］

其中，系统的所有主动力的虚功δW 可写成如下形式

将(12)式代入(11)式，得到

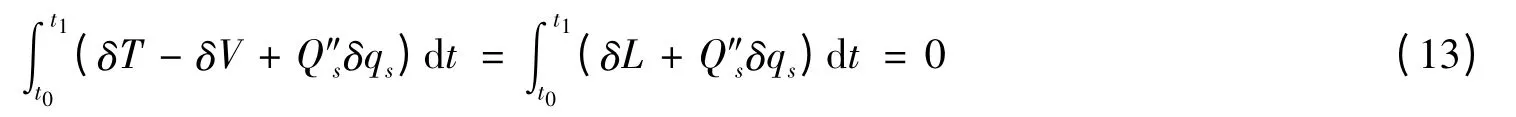
经过变分运算，(13)式可化为

假设系统在始末位置是确定的，则有

故(14)式变为

考虑到积分区间的任意性，由(16)式我们得到

将式(17)与(18)式相加得到

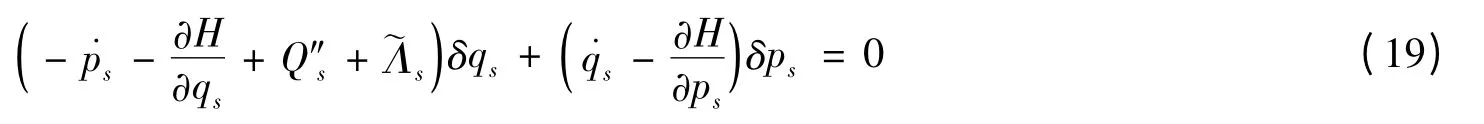
式(19)是相空间中非完整非保守力学系统的微分变分原理.

引进广义变分Δqs，Δps，Δt，其中［7］

其无限小变换分别为

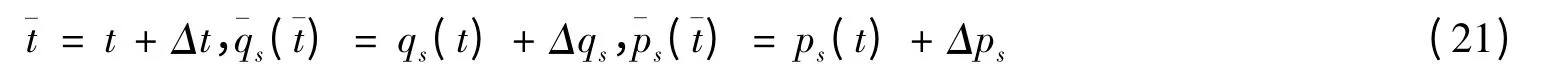
假设

其中ε 为无限小参数，Fs，Gs和f 分别为无限小变换(21)的空间生成元和时间生成元.将式(22)代入到式(20)得到

将(23)式代入(19)式得到

展开(24)式，并注意到

得到

得到下述关系

这就是相空间中非完整非保守力学系统的微分变分原理不变性条件的变换，或称原理(19)在无限小变换(21)下的变形.

2 相空间中非完整力学系统的守恒律

下面给出相空间中非完整力学系统守恒律存在的条件和形式.由式(28)知，如果无限小变换(21)的生成元Fs，Gs，f 和规范函数P 满足如下关系

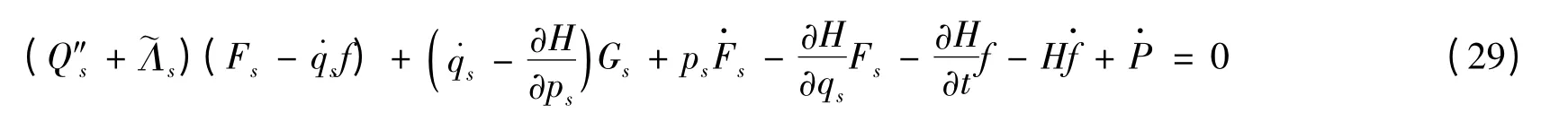
那么系统存在如下形式的守恒律

式(29)可称为广义Noether－Bessel－Hagen 方程，或简称Noether 等式.于是有

定理1 对于相应完整系统(5)，如果存在规范函数P，使得无限小变换(21)的生成元Fs，Gs，f 满足条件(29)，那么系统存在形如式(30)的守恒律.

将式(20)，(21)，(22)代入式(9)，注意到参数ε 的任意性，得到

这是非完整约束(8)对无限小生成元的限制.

将式(31)代入式(29)，条件(29)可表为

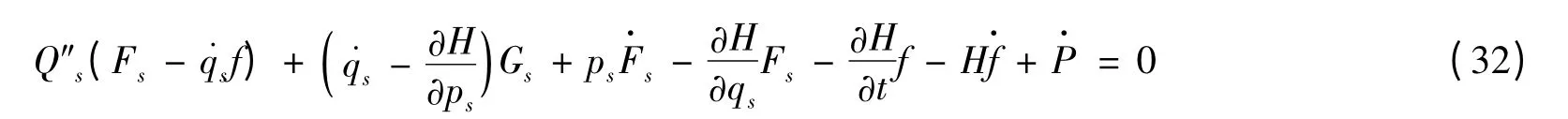
于是有

定理2 对于非完整系统(1)，(3)，如果存在规范函数P，使得无限小变换(21)的生成元Fs，Gs，f 满足关系(32)，且无限小生成元还满足Appell－Chetaev 条件(31)，那么非完整系统存在形如式(30)的守恒律.

条件(31)可放宽为

于是有

定理3 对于非完整系统(1)，(3)，如果存在规范函数P，使得无限小变换(21)的生成元Fs，Gs，f 满足关系(32)，且无限小生成元还满足条件(33)，那么非完整系统存在形如式(30)的守恒律.

3 算 例

例1 系统的位置由两个广义坐标q1，q2来确定，Lagrange 函数为

非完整约束方程为

研究该系统的守恒律［7］.

首先，研究与非完整系统(34)，(35)相应完整系统的守恒律.

引入广义动量和Hamilton 函数

根据运动微分方程(3)以及方程(35)，可解出λ，并将其表示为t，q，p 的函数

根据方程(10)，系统的非势广义力和非完整约束力可表示为

条件式(29)可表为

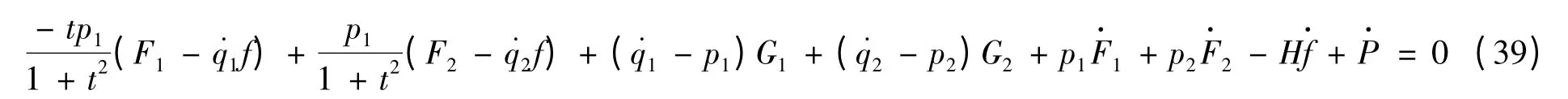
方程(39)有解

对式(40)－(43)，由定理1 中守恒律式(30)分别给出

其中守恒律I1和I2等价.

其次，研究非完整系统(34)，(35)的守恒律.

限制条件(31)给出

容易验证式(42)和(43)满足条件(48)，而式(40)和(41)不满足条件(48)，故此非完整系统守恒律为式(46)和(47).

例2 Appell－Hamel 例.系统的Lagrange 函数为

非完整约束方程为

研究该系统的守恒律.

首先，研究与非完整系统(49)，(50)相应的完整系统的守恒律.

引入广义动量和Hamilton 函数

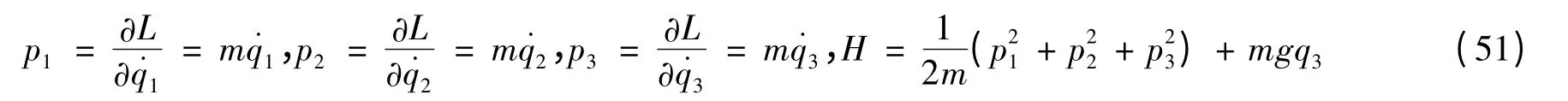
由方程(3)和方程(50)，容易得到

系统的非势广义力和非完整约束力为

条件(29)给出

方程(54)有解

相应于式(55)－(60)，由定理1，得到如下守恒律

其次，研究非完整系统(49)，(50)的守恒律.

限制条件(31)给出

容易验证式(55)－(58)满足条件(67)，而式(59)和(60)不满足条件(67)，故此非完整系统守恒律为式(61)－(64).

4 结 论

本文给出了相空间中非完整力学系统的微分变分原理(19)，并且给出了其在无限小变换下的不变性条件式(29)，进而导出了相空间中相应完整力学系统的守恒律，进一步得到了相空间中非完整力学系统的守恒律.主要结果为相空间中非完整非保守系统的微分变分原理(19)，原理在无限小变换下的变形(28)，以及三个定理.本文结果表明，利用微分变分原理也可以研究相空间中力学系统的守恒律.

［1］梅凤翔.经典约束力学系统对称性与守恒律研究进展［J］.力学进展，2009，39(1):37－43.

［2］梅凤翔.分析力学(上卷)［M］.北京:北京理工大学出版社，2013.

［3］梅凤翔.分析力学(下卷)［M］.北京:北京理工大学出版社，2013.

［4］陈滨.分析动力学(第二版)［M］.北京:北京大学出版社，2012.

［5］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.

［6］梅凤翔，刘端，罗勇.高等分析力学［M］.北京:北京理工大学出版社，1991.

［7］梅凤翔.李群李代数对约束力学系统的应用［M］.北京:科学出版社，1999.

［8］刘端.非完整非保守力学系统的守恒律［J］.力学学报，1989，21(1):75－83.

［9］梅凤翔.利用Jourdain 原理研究二阶非完整系统的守恒律［J］.北京理工大学学报，1998，18(1):17－21.

［10］Zhang Yi，Mei Feng－Xiang.A study of conservation laws of systems with unilateral constraints by means of the differential variational principles［M］.Proceedings of the third international conference on nonlinear mechanics，Shanghai University Press，1998.759－763.

［11］李元成，梁景辉，张毅，梅凤翔.事件空间中单面完整约束系统的守恒律［J］.北京理工大学学报，2000，20(1):21－24.