环F4+νF4上的二次剩余码
2014-06-01高芳
高 芳
(池州学院 数学与计算机科学系,安徽 池州 247000)
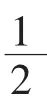
1 预备知识

2 主要结论
当P≡-3(mod)8 时,令
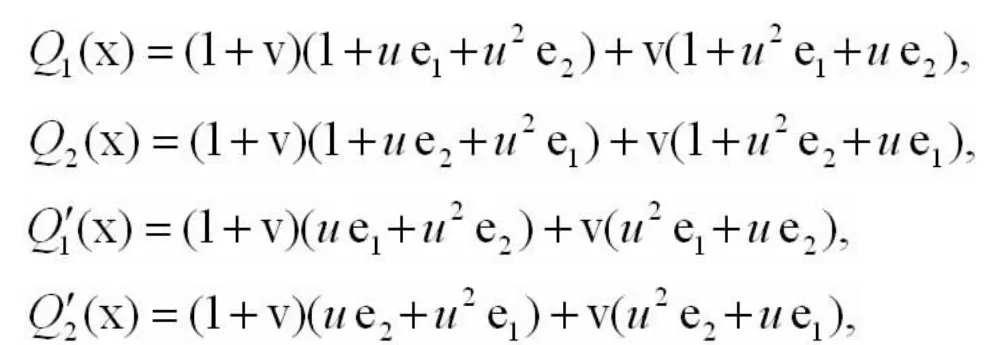
当P≡3(mod)8 时,令

当P≡-1(mod)8 时,令

当P≡1(mod)8 时,令

以下结论成立:


Q1+Q2的幂等生成元为:
[(1+ν)(1+a)+ν(1+b)][(1+ν)(1+b)+ν(1+a)]-[(1+ν)(1+a)+ν(1+b)][(1+ν)(1+b)+ν(1+a)]=1+a+1+b-(1+a)(1+b)=1,即有 Q1+Q2=(F4+νF4)[x]/(xp-1),

(2) 由(1)可得:



Q1+Q2的幂等生成元为:
(1+ν)a+νb+(1+ν)b+νa-[(1+ν)a+νb][(1+ν)b+νa]=a+b-ab=1,
因此 Q1+Q2=(F4+νF4)[x]/(xp-1),

(2) 由(1)可得:

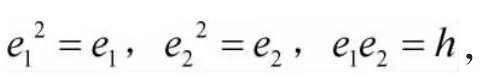
[(1+ν)e1+νe2][(1+ν)e2+νe1]=(1+ν)e1e2+νe1e2=e1e2=h,即Q1+Q2的幂等生成元为:
[(1+ν)e1+νe2]+[(1+ν)e2+νe1]-[(1+ν)e1+νe2][(1+ν)e2+νe1]=e1+e2-νe1e2=e1e2=1,
则 Q1+Q2=(F4+νF4)[x]/(xp-1),
同理


当P≡1(mod)8 时,
[(1+ν)(1+e1)+ν(1+e2)][(1+ν)(1+e2)+ν(1+e1)=(1+ν)(1+e1+e2)+v(1+e1+e2)=1+e1+e2=h,即有
Q1+Q2的幂等生成元为:
[(1+ν)(1+e1)+ν(1+e2)]+[(1+ν)(1+e2)+ν(1+e1)
[(1+ν)(1+e1)+ν (1+e2)][(1+ν)(1+e2)+ν (1+e1)]=e1+e2-(1+e1+e2)=1,
[(1+ν)e2+νe1][(1+ν)e1+νe2]=e1e2=0

(2) 由(1)可得:

[1]Pless V S,Qian Zhong qiang.Cyclic codes and quadratic residue codes over[J].IEEE Trans Inform Theory,1996,42(5):1594-1600.
[2]Jian Gao,Yun Gao.Some Results on Linear Codes over Z4+νZ4[DB/OL].(2014-02-27).http://arxiv.org/abs/1402.6771.
[3]Kaya A,Yildiz B,Siap I.Quadratic Residue Codes over Fp+νFpand their Gray Images[DB/OL].(2013-05-20).http://arxiu.Erg/abs//305.4508.
[4]MacWilliams,F.J.and Sloane,N.J.A.The Theory ofError correcting codes[M].New York:North-Holland,1977.
