各种粒子方程及其可能的发展和意义

张 一 方

(云南大学 物理系，云南 昆明 650091)

0 引 言

各种方程的研究在粒子物理中始终是一个重要问题.Jain 等讨论了背景场的运动方程、顶点算符Virasoro 条件下显现的对顶点函数的波方程和弯曲空间中的弦动力学［1］.Hayward 得到从弦理论的低能考虑呈现出的二维模型，及超光速快子(tachyon)等的方程和相应的特解［2］.Niz 等讨论了宇宙演化中的弦和M理论及其方程［3］.笔者基于微观的波动－粒子的二象对称性，把各种波动的物理量代入经典力学方程，得到力学波动论;进而提出量子理论中的一些新算符和非线性方程［4］.在探讨微观相对论的基础上，又提出极小时空的光速应存在统计起伏，而且在高维柱形卷曲空间中光速是可变的和量子化的.由此讨论修改、发展相对论和量子论的可能的某些方法，并提出存在势和相互作用时几种新的量子力学方程［5］.最近笔者探讨了粒子物理中的各种统一.它们包括相互作用统一和规范场，场、粒子及其方程的统一，低高能时的统一，统一和非线性理论的关系等.并提出它们也许可以统一到统计性［6］.基于粒子的动力学模型及其拉氏量和方程，进行了某些更深入的研究和应用.它可以联系于袋模型;方程的解联系于各种势;其简化的振动－转动模型和谐振子模型等导致各种质量公式.由此可以讨论强子的某些质量公式，并提出动力学模型可能的发展方向［7］.

已知的Schrodinger 方程、Dirac 方程和Klein－Gordon(KG)方程等在粒子物理中都是非常重要和非常基本的.它们可以由拉氏密度得到［8］.在此讨论由这些方程彼此结合得到的某些新方程.量子力学的基础是波粒二象性［9］，对其简化的各种振动提出相应的方程.由对称性破缺时的方程及其推广，讨论各种解.进而探讨粒子方程及其解，以及和混沌的关系.

1 已知的粒子方程及彼此结合得到的方程

粒子物理中各种已知的方程都可以由拉氏密度得到.拉氏密度是［10］:

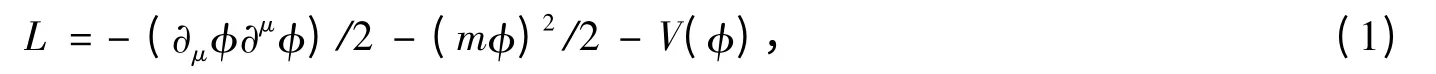
由此得到有势的标量场KG 方程:

对QCD，非Abel 场的拉氏密度是［10］:

由此可以得到有相互作用的旋量场Dirac 方程和矢量场Proca 方程.对一维拓扑孤子方程积分得U=(β/4)［φ2－(m2/β)］2，U=0，φ=是Higgs 理论.G.’tHooft SO(3)规范不变的拉氏密度是［10］:

目前的Dirac 方程，KG 方程等都是自由粒子且质量不变的一阶、二阶方程.它们应是基态粒子(e，p 及π介子)的方程.两种方程结合就是新的方程:

相应的Schrodinger 方程是:

推广为四维就是

这可以结合动力学破缺，得到［9］

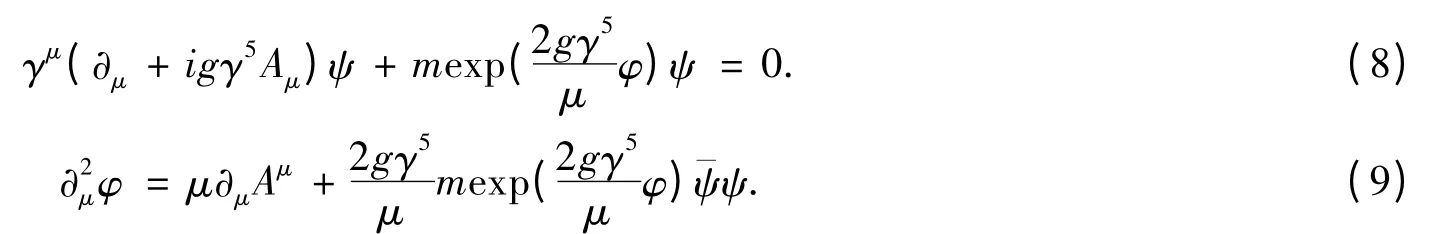
或者结合Higgs 破缺，得到［9］

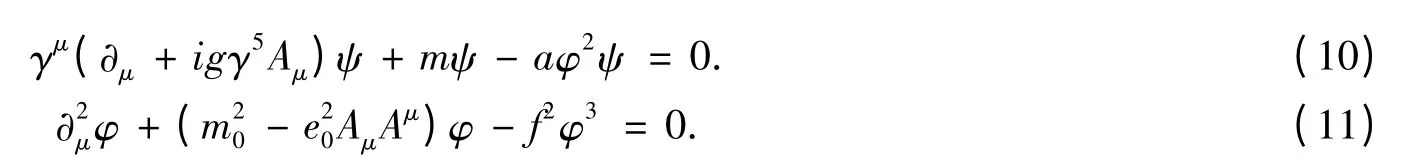
由此又联系于动力学模型，导致GMO 质量公式及其修改的完全符合实验的更精确的质量公式［9，11，12］:

最近笔者由一般的具有振动和转动两种运动状态的突现弦(emergence string)方程就可以得到粒子的GMO质量公式及(6)，并导致对称的强子寿命公式［12］.由QCD 破缺的动力学模型可以得到质量公式，由Weinberg－Salam 理论或其破缺应该得到轻子质量公式.

2 由振动得到的粒子方程

由量子力学基础的波粒二象性［9］，最简单时就联系于振动.强迫非简谐振子是

这个方程有混沌解.无强迫项b=0 时，如果k=0 就是化为常微分的Higgs 方程.如果x″=0 就是化为常微分的Heisenberg 统一方程［13］.x″≠0 和k≠0 则类似化为常微分的非线性Dirac 方程的平方:

的第一项.

有一般场(g=e 时是电磁场)时，广义动量为

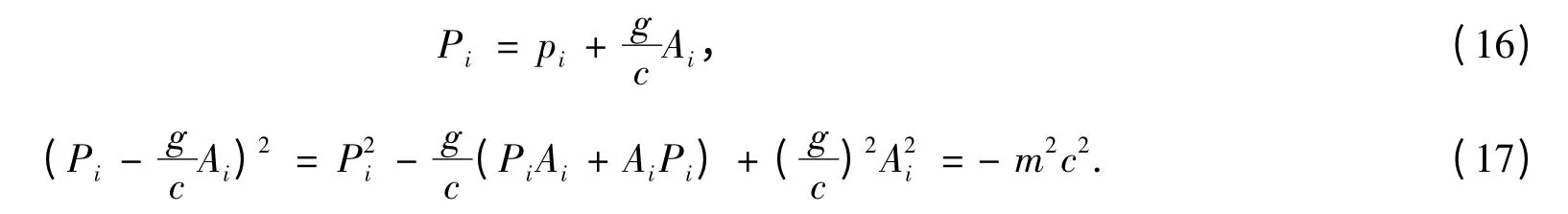
相应方程为:

这是KG 场与一般场相互作用的方程.Pauli 由此导出自旋磁矩.

方程(5)(6)(7)(18)类似阻尼波方程.与(18)比较则

此时解为

这是减幅波动.这也许可以联系于质量可变，特别当方程(5)(7)中β 修改为随时间变化的量时.进而还可以结合非线性方程.当阻尼很大时，振动非周期，就无法显示波动性.受迫振动、阻尼振动在一段时间后达到稳定就是谐振动，质量不变相应于衰变后化为基态粒子.

3 对称性破缺的方程及其推广和各种解

由Higgs 破缺，Aμ=0，由标量场方程(11)得扭子解

在动力学模型、振动－转动模型(ORM)［9，7］中描述衰变、碰撞.对这些方程，能级就是质量公式［9，12］.假定解对应S 矩阵，二者分别相应于方程和Feynman 规则，二者结合，解的平方就相应于跃迁几率.跃迁不同，系数不同就分别是衰变宽度和碰撞截面.

方程及解中引入跃迁可以结合统计方程的意义，其中有几率跃迁和衰变的动力学基础，或二者再结合.对后者，衰变是自由粒子方程［9］，碰撞是相互作用方程，末态由x=∑mf/∑Mi决定，又x=cosθ=pz/p，即球体是初态球，z 方向是末态.p－pz=纯动量就是x－y 平面，这与Dalitz 图有关.

简单的φ－ψ 耦合场方程为:

它们化为常微分方程组是

二者结合得高阶方程:

如果作为偏微分方程组化为高阶方程则是:

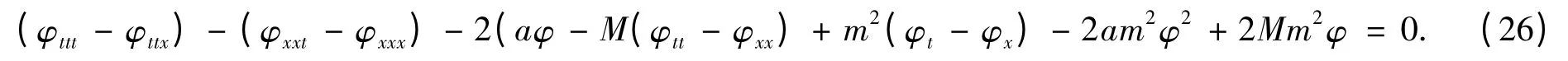
这是一类新的三阶非线性常微分及偏微分方程.与笔者的统计方程形式［14］有类似处.M=0 是中微子等，方程化为

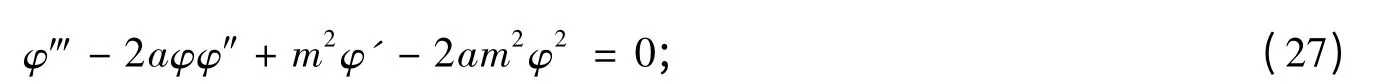
m=0 是Goldstone 粒子，方程化为

其解是φ=Ce2ax+(M/a)和φ=ax+b.

对动力学破缺，

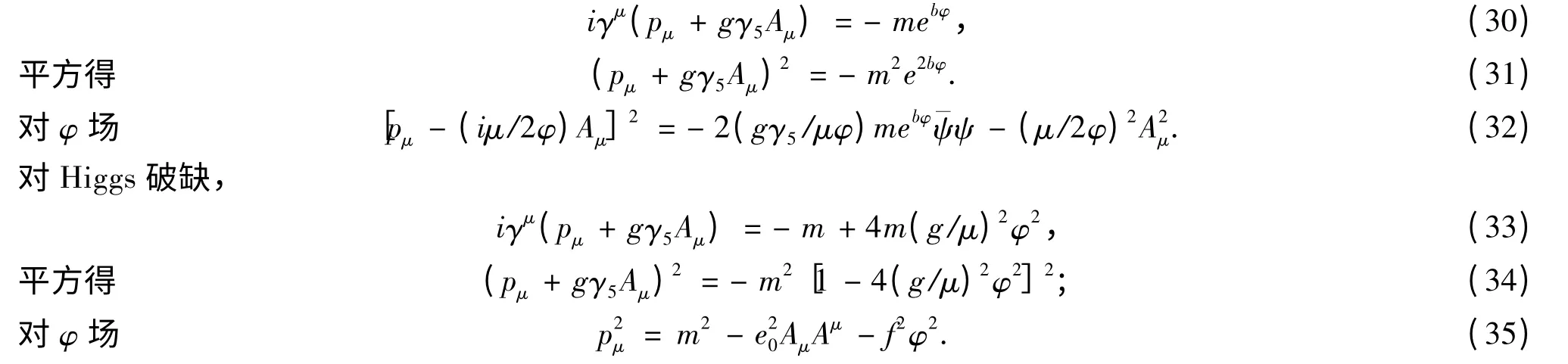
作为玻色子场，规范场、矢量场是改变其他场的pμ;而标量场是改变其他场的质量，其相互作用都可化为等价于附加质量.如φ－ψ 相互作用

φ－Aμ相互作用

这类似Higgs 标量场导致其他矢量介子、轻子获得质量.此外，各种场的自相互作用都可化为附加质量.SU(2)、SU(3)的规范理论、方程也如此.作为费米子旋量场总是成对出现珔ψψ，并导致其他场(φ，Aμ)的流J.

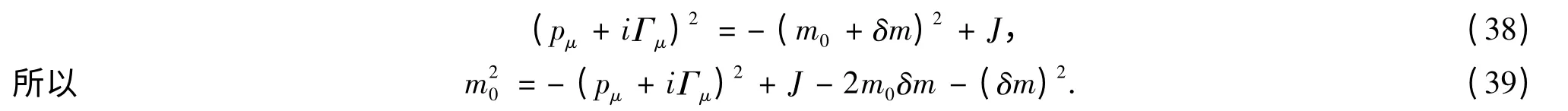
这类似重整化.自由粒子的裸m0与相互作用粒子的质量不相同.而m0不论各量如何改变都不变，这也是一种群.类似Lorentz 群中的ds2不变及重整化群.

4 各种其他的粒子方程

Weyl 的中微子方程是二分量方程［8］

它可以描述宇称不守恒.这推广到m≠0 的方程，根据空时对称性，应可以类似构成时间反演不成立的方程，否则时空此时不对称.m=0 及m≠0 的方程，可能也是二分量方程，仅矩阵σ 不同.由此再反之推广到狭义、广义相对论等.最后方程统一为Weyl 方程，表明此时宇称P 不守恒，或对称的时间反演(宙称)不成立.进一步，把GL(m，C)，SU(N)，SO(N)等各种群都推广到时间反演不成立的群、半群等.时间反演不成立的结果可以有若干种，但最后所取的形式应结合宙称不成立的粒子是有演化方向(如衰变)的粒子，特别是K0L.

Langevin 方程

与Boltzmann 微积分方程

其最后一项是非线性项，形式相似.而Boltzmann 方程描述了趋向平衡的过程.达到平衡时.如果结合量子力学Heisenberg－Liouville 方程

则平衡时方程化为

对应量子力学和Maxwell－Boltzmann(MB)分布、Γ 分布.非平衡时，非线性的Dirac 方程，解为

对应Fermi－Dirac 统计［9］.方程对应有非线性项的Langevin 方程和Heisenberg－Liouville 方程的推广.非线性KG 方程对应于Bose－Einstein(BE)统计.量子统计也是平衡态.解f=A/(eαt+n)，则方程为

n≠0 对应量子统计(n=±1)，非线性项.此时非线性方程与非线性的量子力学方程相关，仅仅f=|ψ|2=分布.如果df/dt=［f，H］+Q=－α'f，则α'=α(1－nf/A).

由有相互作用项j 的场方程

可得费米子iγμpμ+μ=j/ψ，玻色子=－m2+J/φ(Jμ/Aμ)，所以费米子重整化质量平方为μ2+(j/ψ)2－2μj/ψ，玻色子m2－J/φ 与相互作用有关.如φ－ψ 场［8］，

非线性方程对应于相互作用和有势场.而QCD，动力学模型就联系于很多非线性方程.如:1)Higgs 破缺标量场，并发展为KdV 推广方程;还直接导致立方KG、Dirac 方程等.2)QCD，无破缺时导致立方Schrodinger方程.3)Hirota 方程是立方Schrodinger 和KdV 方程的结合.4)Boussinesq 方程类似Sine－Gorden 方程，有相互作用.而例子1).3).4).又都对应导数耦合.

QCD，ψ－Aμ方程包括立方Schrodinger 方程，其可化为

对应KdV 推广方程及Higgs 方程［16］.

5 粒子方程的解和混沌

由线性及非线性Dirac 方程等可以得到离散解.目前量子力学中是能级离散.对Yang－Mills 规范场、广义相对论方程、GL(6，C)及各种统一方程都应该如此.

非线性方程的随机解，不断分岔可以用于高能多重产生、级联簇射、统计性等粒子物理领域［23，9］.方程解普适，对应于多重产生等的普适、简并，即对各种粒子都成立，并且高能时统计性统一［11］.这可能还与重整化、发散的普适性有关.此时参数λ 相当于阈值.一定的λ 才有不动点x*(对应粒子)及其稳定性，p 点周期等.λ→λ∞对应于高能.λ＜λ∞有2n个稳定的不动点，Henon 变换的奇异吸引中心，可能对应于衰变和级联簇射.非线性方程组对应Dirac 耦合方程.Dirac 方程用孤子方法化为常微分方程是

由此就可以联系于混沌方程.以质量m 为参数λ，m→α－1=λ0=0.3995 可能对应u，d 夸克－部分子的质量1.7－3.3 MeV 和4.1－5.8 MeV［24］.由此讨论非线性Higgs 方程等的叠加及混沌解.或者以Higgs 场或其m 为参数λ.这时可能已经不是非线性映象了.

轫致辐射、电磁簇射(与物质相互作用，e－→e－γ，γ→e+e－)都是二分叉.光子能量εγ＜2mec2时簇射停止，这相当于参数λ.但是一般量子方程中无这参数.宇宙线超高能粒子与原子核碰撞的广延大气簇射，粒子数可达1012个.电磁簇射都是电磁相互作用及其旋量场、矢量场的方程组.n→∞对应于高能极限，泛函方程类似标度律.vW2趋于常数约为1/3，近似于λ0.

联系于重整化群方程的Callan 等的标度性，类似Feigenbaum 泛函方程

KNO 标度，Dao 标度都是高能时的结果.相应的Pearson 方程是线性的，符合泛函方程.

粒子与混沌的关系可能是，稳定性条件1＜λ＜3，与三个夸克，分数夸克电荷(1/3，2/3)，粒子三代等有关.一个粒子可以三分岔为夸克，或四分岔为(u，d，s，c)等等.而能量特大时，多分岔为砂子(sandon)［9］.这就是非线性方程统计性混沌解与粒子的多层次－状态模型(MSSM)的关系［9］.如果

是三分岔，则是非线性方程，Heisenberg 统一方程［13］，其与SU(3)对称性方程一致，导致高能(阈λ→λ∞)或小距离(λ=1/r→1/r0)时是三夸克、砂子及统计性.分岔可以是衰变，级联衰变.如1→2→3 是二体衰变(粒子或夸克对)再化为三夸克等;或者1→3→2 是三夸克又衰变为二体等等.混沌理论的普适性此时和粒子种类无关，即与方程无关.这与重整化，标度性等对应，特别是标度因子.它也说明超高能时统计混沌的很多性质都是独立的，这正好对应于统计性.0＜λ＜1 时=0 是稳定不动点，对应真空基态;=1－(1/λ)是不稳定的不动点，对应不稳定粒子，如μ，π 等;1＜λ＜3 时是不稳定不动点，对应真空自发破缺是稳定不动点，对应p，n 等;而λ ≧1 时真空开始自发破缺.

非线性方程由混沌达到定态.在变化的时间内很复杂，由统计性决定.这相应于粒子和奇点的关系:稳定奇点(或焦点)对应稳定粒子(如v.e，p).不稳定结点对应亚稳定粒子.

按照一般的非线性理论，各种非线性量子理论中都应该有孤子和混沌.QCD、超对称性等都是非线性的，其中应该有混沌.高能时一方面是统一［11］，另一方面是混沌，而混沌也是一种统一［9］.笔者提出某些非线性方程具有孤子和混沌双解，二者成立的条件不同，某些参数是某个常数时得到孤子，而这些参数在一定区域变化时出现分岔－混沌.这种双解可能对应于量子理论中的波－粒二象性，并探讨了其在数学、物理、粒子理论及神经系统中可能存在的新的意义［25，26］.

量子混沌必须非线性量子理论［9，27，28］.这可能应该推广混沌概念本身.量子混沌主要是n＞58，59 的高激发态.此时的混沌应联系于Pauli 不相容的可能破缺［29］.混沌就是轨道随机不分明，出现混沌也就开始相容.但轨道电子原来已是统计性的电子云，这与混沌应该存在关系.更一般，研究量子论中的与混沌不相容的各个方面.这样如果发现混沌则它们就不成立.如果高激发态原子混沌则相容［9，30］，这样粒子内部混沌也应相容.结合超对称性，还可以引入超混沌(hyperchaos).

总之，基于已知理论和方法，探讨新的方程及其解，并用于粒子物理，必然是有意义的.

［1］Jain S，Mandal G，Wadia S R.Virasoro conditions，vertex operators，and string dynamics in curved space［J］.Phys.Rev.，1987，D35(2):778－781.

［2］Hayward J D.String－motivated model［J］.Phys.Rev.，1995，D52(2):1019－1025.

［3］Niz G，Turok N.Classical propagation of strings across a big crunch/big bang singularity［J］.Phys.Rev.，2007，D75(2):026001.1－21.

［4］张一方.力学波动论，量子理论中的新算符和非线性方程［J］.云南大学学报，2000，22(1):37－40.

［5］张一方.极小时空的光速和相对论及某些新的量子力学方程［J］.云南大学学报，2011，33(2):164－168.

［6］张一方.粒子和场方程的统一［J］.商丘师范学院学报，2012，28(12):39－45.

［7］张一方.粒子的动力学模型的应用和强子的质量［J］.商丘师范学院学报，2013，29(6):28－33.

［8］罗曼P.基本粒子理论［M］.蔡建华，龚昌德，孙景李，译.上海:上海科学技术出版社，1966.

［9］张一方.粒子物理和相对论的新探索［M］.昆明:云南科技出版社，1989.Phys.Abst.1990.93，1371.

［10］Weinberg S.The Quantum Theory of Fields［M］.V1.Cambridge，2001.

［11］Chang Yi－Fang，High energy behavious of particles and unified statistics［J］.Hadronic J，1984，7(5):1118－1133.

［12］Chang Yi－Fang.From emergence string to mass formulas of hadrons and symmetric lifetime formulas of hadrons［J］.International Review of Physics，2012，6(3):261－268.

［13］Heisenberg W.Introduction to the Unified Field Theory of Elementary Particles［M］.Interscience Publishers，1966.

［14］张一方.统计分布形式上的统一和各种分布相应的方程［J］.云南大学学报，1986，8(1):76－82.

［15］王竹溪，统计物理学导论［M］.北京:高等教育出版社，1956.

［16］陈庆益，数学物理方程［M］.北京:人民教育出版社，1979.

［17］Chatrchyan S，Cifuentes J A B，Cabrillo I J，et al.Combined results of searches for the standard model Higgs boson in pp collisions at=7 TeV［J］.Phys.Lett.，2012，B710(1):26－48.

［18］ATLAS Collaboration(Aad G，Gray H M，Marshall Z，et al.).Combined search for the Standard Model Higgs boson using up to 4.9 fb－1of pp collision data at=7 TeV with the ATLAS detector at the LHC［J］.Phys.Lett.，2012，B710(1):49－66.

［19］Draper P，Meade P，Reece M，et al.Implications of a 125 GeV Higgs boson for the MSSM and low－scale supersymmetry breaking［J］.Phys.Rev.，2012，D85(9):095007.1－6.

［20］Higgs P W.Broken symmetries and the masses of gauge bosons［J］.Phys.Rev.Lett.，1964，13(16):508－509.

［21］Higgs P W.Spontaneous symmetry breakdown without massless bosons［J］.Phys.Rev.，1966，145(4):1156－1163.

［22］Kibble T W B.Symmetry breaking in non－Abelian gauge theories［J］.Phys.Rev.，1967，155(5):1554－1561.

［23］张一方.用推广的混沌理论描述多重产生和级联簇射［J］.新疆大学学报，1986，3(3):1－5.

［24］Nakamura K，Hagiwara K，Hikasa K，et al.Particle Data Group［J］.J.Phys.，2010，G37(7A):25－86.

［25］张一方.某些非线性方程的双解:孤子和混沌及其意义［J］.云南大学学报，2004，26(4):338－341.

［26］Chang Yi－Fang.Neural synergetics，Lorenz model of brain，soliton－chaos double solutions and physical neurobiology［J］.NeuroQuantology，2013，11(1):56－62.

［27］Chang Yi－Fang.The nonlinear quantum theory and possible violation of the Pauli exclusion principle［C］.Proc.of the 4th Asia－Pacific Phys.Conf.(Ahn，S.H.et al.，eds)，V2.World Scientific，1991.1483－1486.

［28］Chang Yi－Fang，Test of Pauli’s exclusion principle in particle physics，astrophysics and other fields［J］.Hadronic J.，1999，22(3):257－268.

［29］Chang Yi－Fang.Some possible tests of the inapplicability of Pauli’s exclusion principle［J］.Hadronic J.，1984，7(6):1469－1473.

［30］张一方.在激光导致的高激发态原子中检验泡利不相容原理的适用性［J］.自然杂志，1988，11(8):635－636.