五点数值微分公式及其外推算法

夏爱生，夏军剑，张会鹏

(军事交通学院 基础部，天津300161)

目前的《数值分析》教材都给出了插值型的二阶三点(等距)数值微分公式，并给出中间节点x2的余项，其截断误差为O(h2)，该公式精度较低且没有给出一阶和二阶五点数值微分公式及其余项。本文首先推出了中间节点x2处一阶五点数值微分公式和二阶五点数值微分公式，然后求出其截断误差的渐进展开式，利用Richardson 外推算法提高节点x2处数值微分公式的精度和其收敛阶数。

1 中间节点x2 一阶和二阶五点数值微分公式

设f(x)为定义在区间上［a，b］的函数，给定f(x)在节点a=x0＜x1＜x2＜x3＜x4=b处的函数值为f(xk)(k= 0，1，2，3，4)。且x0、x1、x2、x3、x4为等距节点，即x4-x3=x3-x2=x2-x1=x1-x0=h，f(x)在x2的某领域U(x2，δ1)内任意次可微［1］。

由

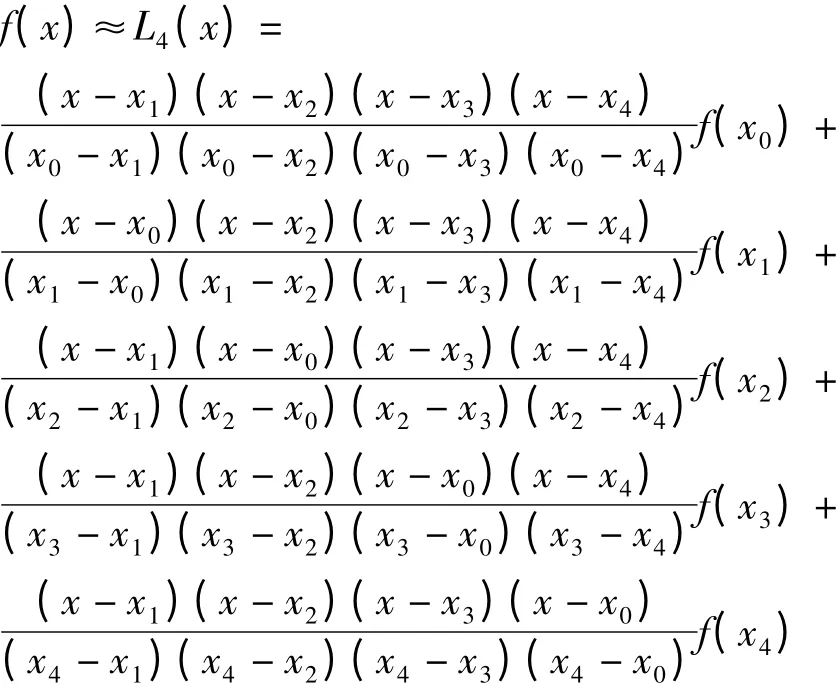
得到

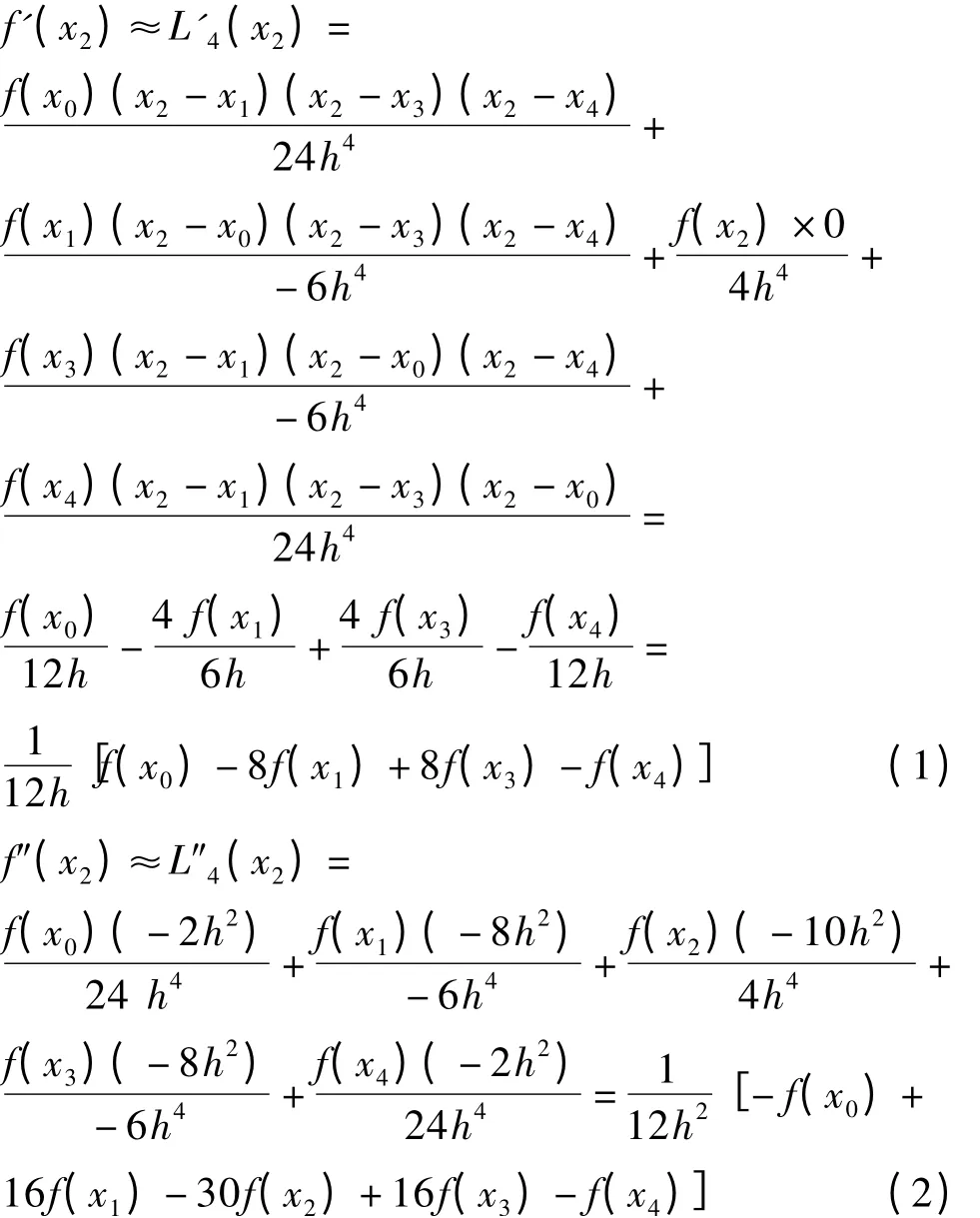
式中L4(x)为4 次Lagrange 插值多项式。

2 中间节点x2 一阶和二阶数值微分公式的外推

根据已知条件，利用Taylor 公式，分别将f(x0)、f(x1)、f(x3)和f(x4)在U(x2，δ1)内展开成泰勒级数［2］:

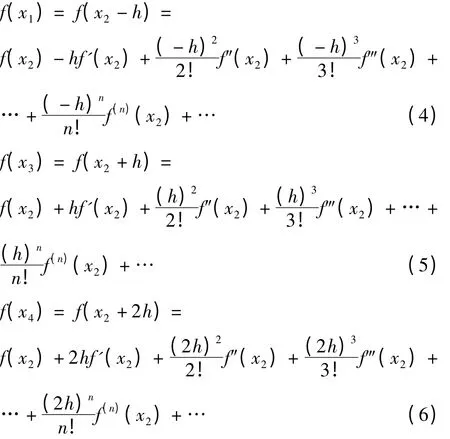
将式(3)—(6)代入式(1)，得到［3］

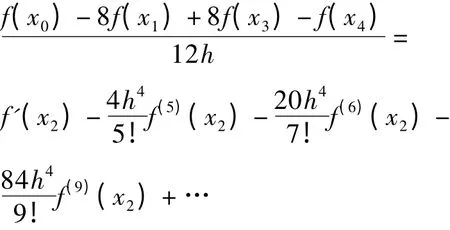
所以

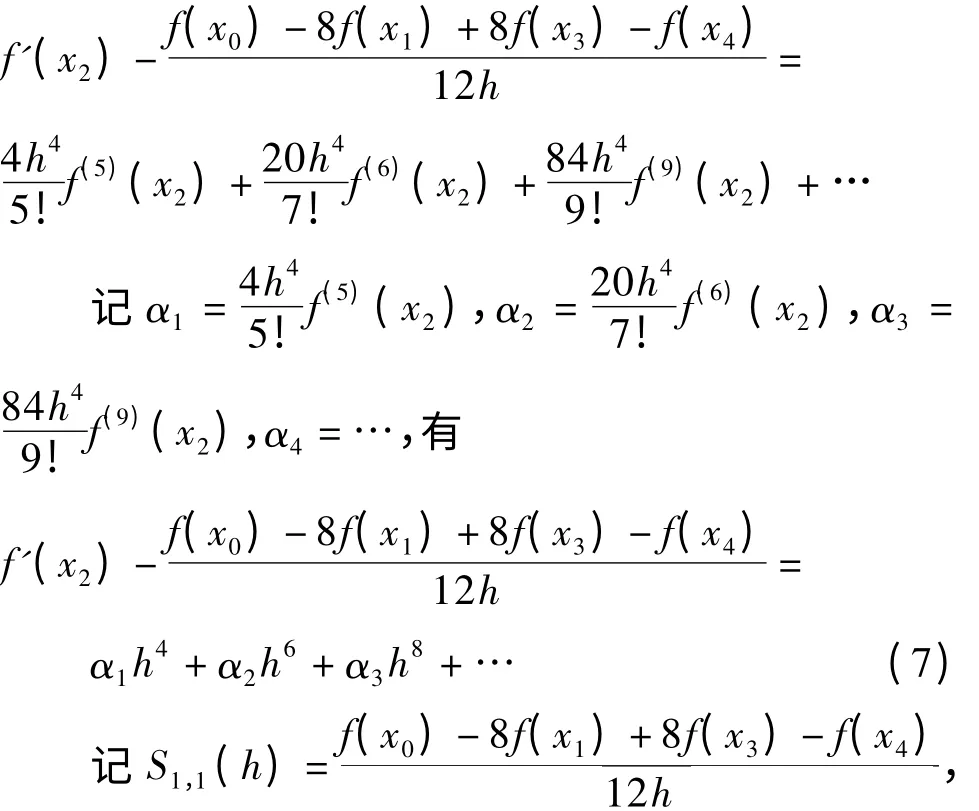
有

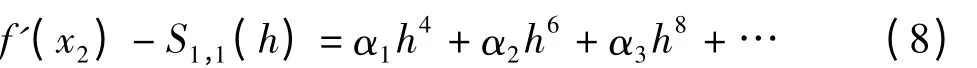
对于固定节点x2，显然是与h无关的常数。故式(8)符合Richardson 外推算法［4］，所以有

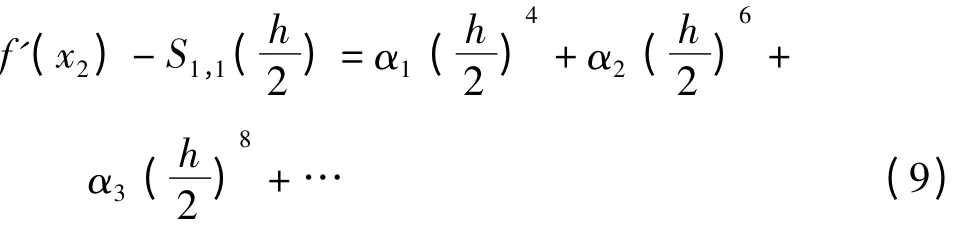
由16 ×式(9)-式(8)，得到

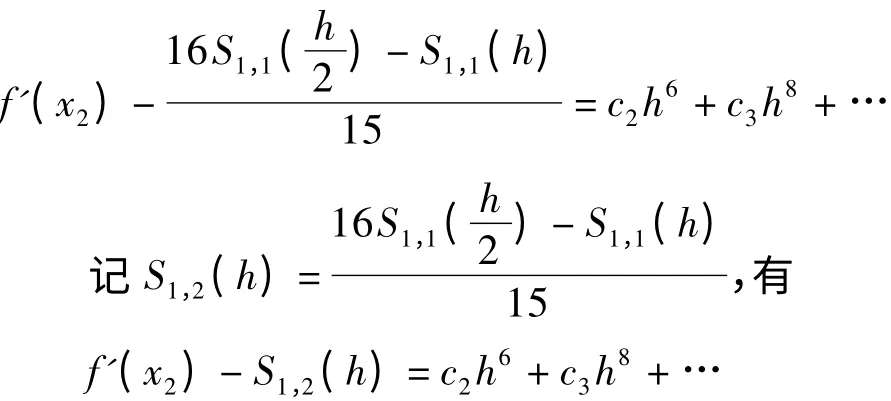
以此类推，可递推序列如下

式中S1，k+1(h)的截断误差为O(h2(k+2))，且k=1，2，…。

利用Richardson 外推算法经次外推后得到高精度的一阶数值微分公式f'(x2)≈S1，k+1(h)，将截断误差由原来的O(h4)减小为O(h2(k+2))，k=1，2，…。

将式(3)—(6)代入式(2)，得到

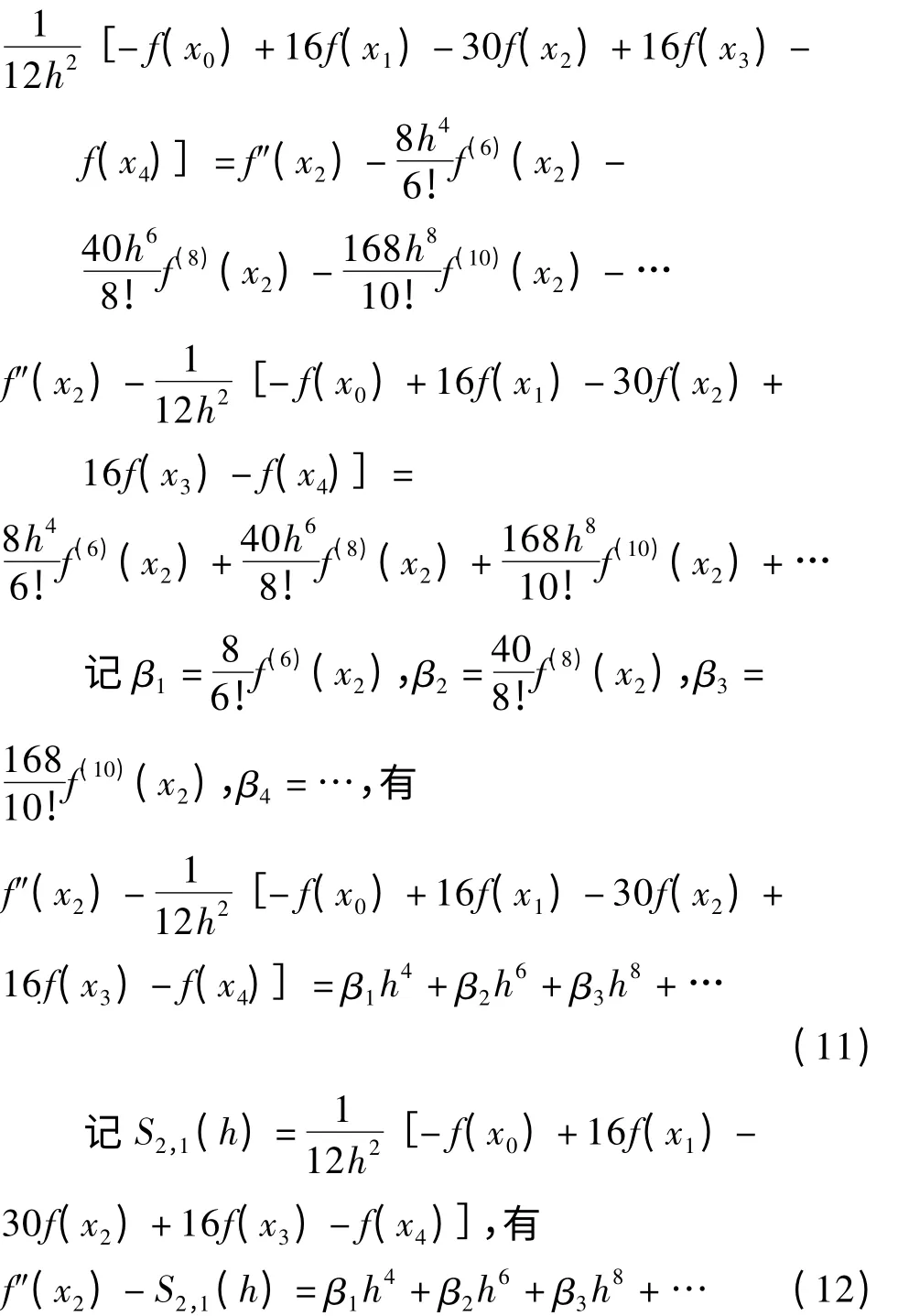
对于固定节点x2，显然是与h无关的常数。故式(12)符合Richardson 外推算法［4］，所以有

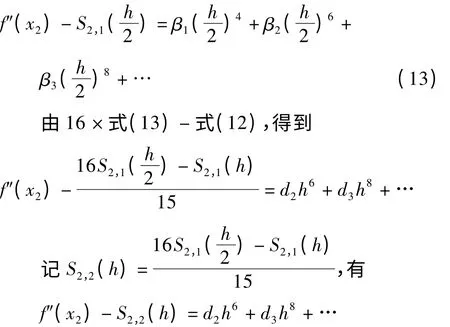
以此类推，可递推序列如下

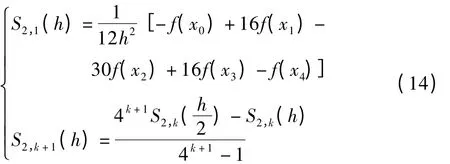
式中S2，k+1(h)的截断误差为O(h2(k+2))，且k=1，2，…。

即利用Richardson 外推算法经k次外推后，得到高精度的二阶数值微分公式f″(x2)≈S2，k+1(h)，将截断误差由原来O(h4)减小为O(h2(k+2))(k=1，2，…)。

3 结 语

通过本文的推导分析，中间节点x2的一阶、二阶数值微分公式经k次外推后得到的公式能以较快的速度收敛于精确值，且其截断误差减小为O(h2(k+2))(k=1，2，…)，其精度大大提高。

［1］ 翟瑞彩，谢伟松. 数值分析［M］. 天津:天津大学出版社，2000:201-212.

［2］ 同济大学应用数学系.微积分:上册［M］.北京:高等教育出版社，2000:141-149.

［3］ 同济大学应用数学系.微积分:下册［M］.北京:高等教育出版社，2000:287-306.

［4］ 邓建中.Richardson 外推算法及其应用［M］.北京:科学出版社，1999:125-201.