带延误的多机型航空战略投送兵力分配模型

张 昕，苑德春，潘 璠

(1.军事交通学院 联合投送系，天津300161;2.军事交通学院 军事交通运输研究所，天津300161)

战略投送能力是衡量一个国家未来作战能力的重要指标，而战略空运则是国家战略投送的重要组成部分，是夺取军事制高点的战略筹码。一方面，随着国家综合实力的增强以及战略格局的宏观运筹，发生外敌对我军实施大规模陆上入侵的可能性越来越小，但在与国家核心利益密切相关的热点方向，发生局部战争的可能性增大。另一方面，随着国家利益拓展，能源与资源的稳定供给对国家经济的长远发展影响重大;频发的重大自然灾害对人民生命财产构成严重威胁;社会转型期的矛盾突显，突发公共事件对社会稳定构成严重冲击。面对传统安全威胁与非传统安全威胁，建设强大的航空战略投送力量十分迫切。

一直以来，国内对航空战略投送兵力分配的研究停留在点对点式的直达航线，投送兵力的规模想定也偏小。但在实际的投送过程中，能够称之为战略投送的，必须是远距离、大规模的多种机型混合运输。因此，本文主要研究带延误的多个机场航线网络中多种机型的兵力分配模型。

1 模型的建立

1.1 基本假设

在战略空运过程中，假设以军、民航大型机场为空运平台，现有开通航线为投送网络，飞行计划以战略空运任务为第一优先，同时考虑空域流量的影响和人员在中转机场整备集结再次登机的时间延误，所有分配的兵力任务都试图选择最短航路到达目的地。

1.2 参数说明

给定带延误的多机型航空战略投送兵力分配模型参数(见表1)。

表1 带延误的多机型航空战略投送兵力分配模型参数

中转航段a和b在连接机场网络中连接机场ω 的航段k上，当且仅当航段a和b同样在该航段上，由此满足以下条件:

航段投送量满足以下条件:

航段投送量与航路投送量满足以下关系［2］:

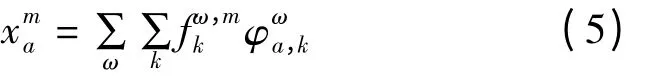
考虑中转机场的时间延误，中转流量与航段流量需满足以下关系:

空域流量阻抗则可以修正为航段阻抗与中转延误阻抗2 个部分之和，即

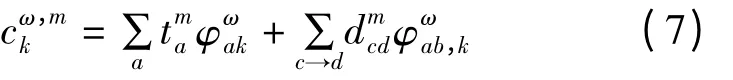
式(7)表明，机场的空域阻抗是由连接该机场的各条航段的流量阻抗及各个中转方向的时间延误阻抗累计而成。

也就是说，机型m在航段a上的投送量对机型l在航段b上的流量阻抗影响一般不等于机型l在航段b上的投送量对机型m在航段a上的流量阻抗的影响。

同理，机型m在中转机场c→d上的投送量对机型l在中转机场g→h上的延误影响一般不等于机型l在中转机场g→h上的投送量对机型m在中转机场c→d上的延误影响。需要指出，这里将时间延误t和空域阻抗d分开处理，并认为前者是航段流量x的函数t(x)，后者是中转流量y的函数d(y)。由式(3)、(5)、(6)可见，x和y之间具有内在关系(由航段中转之间天生的拓扑关系决定)，t和y之间以及d和x之间有间接关系，但是这些关系的正确性不需要用额外约束条件加以强制，而是经由下文中分配算法的特点自动地加以保证。

1.3 建立模型

给定一个存在多种机型飞行的机场航线有向网络G(N，A)［4］，有

可变换为

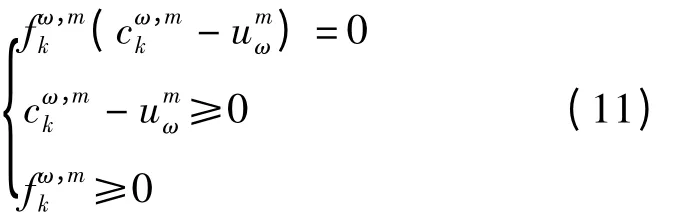
同时，航线、航段、中转方向的投送量和阻抗及其关系需满足式(4)—(7)。

2 求解算法

2.1 求解原理

尽管D-MAMUT 模型结合了多模式以及延误的因素，但在本质上并没有改变该模型作为非对称UE 模型的特点。鉴于精简对角化算法是求解非对称UE 模型的有效算法，因此把该算法作为D-MAMUT 模型求解算法的基本框架，在此基础上得到了考虑多模式和延误的确定型精简对角化算法，称其为D-SAMT 算法。

假设算法在第n次迭代后，得到了航段流量x(n)和中转流量y(n)，这时若机型m在航段Ka上的阻抗函数除了可变外，其余变量均取值于x(n)中的对应项并保持不变，由此得到第n次迭代后可分离的阻抗函数形式，即

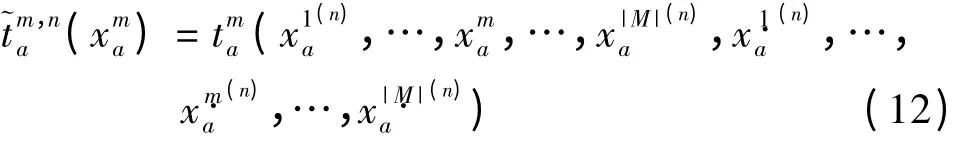
与此类似，可以得到第n次迭代后可分离的中转延误函数形式，即

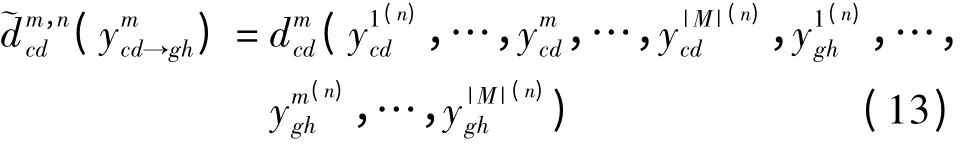
2.2 求解步骤

Step 0:初始化。对∀m，基于执行1 次AON 网络加载，从而得到初始航段流量x(1)和中转流量y(1)。

Step 1:更新。令n=1，对∀m，利用计算及，得到各个

Step 2:确定迭代方向。对∀m，基于及执行1 次AON 网络加载，得到各个附加的航段流量和中转流量

Step 3:确定迭代步长。迭代步长λn由以下一维极值问题决定:

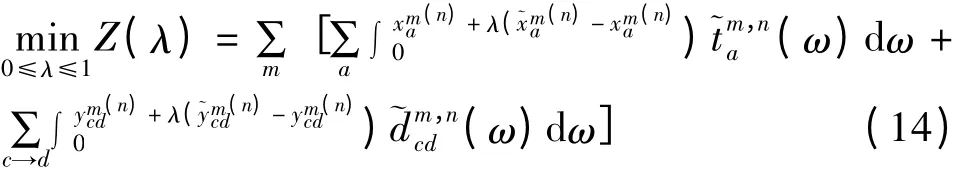
Step 4:确定新迭代点。令x(n+1)=xn+ λn×

3 算 例

3.1 基础数据

假设航线网络A 如图1 所示，由1 号机场向9号机场投送兵力，航线网络中共有12 条航路，飞行机型为A319 和A340，其兵力投送任务量分别为740 人和2 950 人，各条航路上的阻抗参数和延误参数见表2，各航路的中转参数见表3。

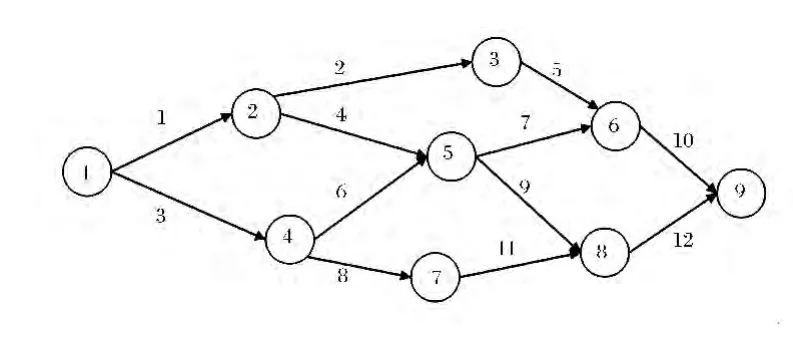
图1 航线网络A 示意图

航段阻抗函数的计算如下:

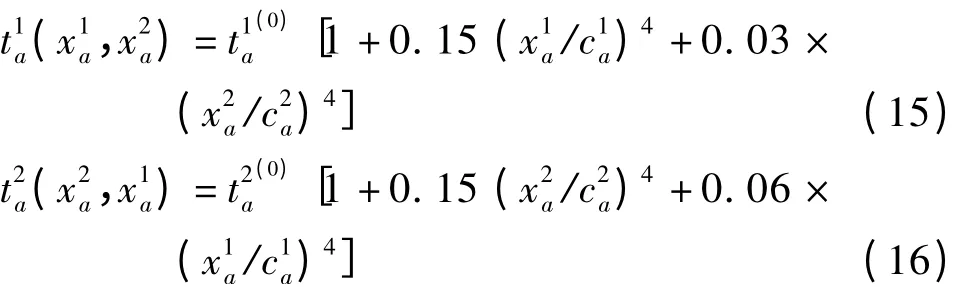
中转延误参数的计算如下:

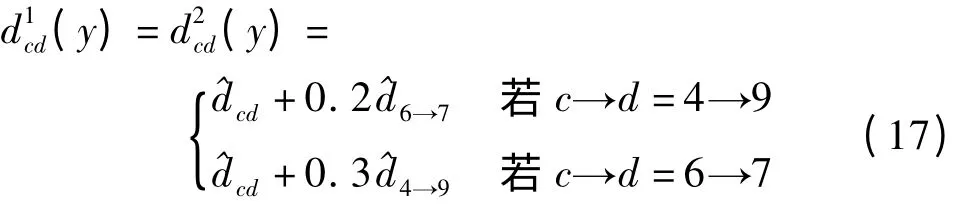
其中

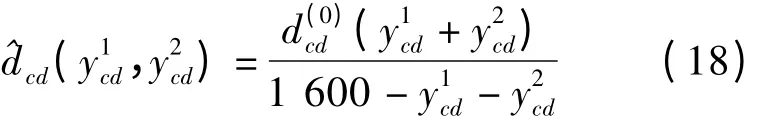
表2 阻抗参数和延误参数

表3 中转参数

3.2 计算过程

求解中，迭代收敛条件是相邻2 次解的最大相对偏差σn小于某个预定精度值ε，即

式中ε=0.01。

3.3 结果分析

当ε=0.01 时，算法在迭代44 次后收敛到平衡解(x*，y*)。此时将各个和ycd=标到对应的航段和中转机场附近，分别如图2、图3 所示。

平衡状态下的航路阻抗和流量见表4。机型A319 在这6 条航路上均有流量存在，并且这些航路阻抗在允许误差范围内可视为相等(约为116.2);机型A340 在6 条航路上也都有流量存在，航路阻抗也都相等(约为86. 8)。这个结果吻合D-MAMUT 模型的基本出发点，即多模式UE 条件。

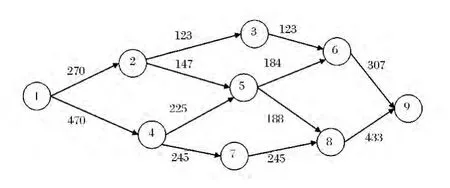
图2 机型A319 在航线网络A 中的兵力分配情况

图3 机型A340 在航线网络A 中的兵力分配情况

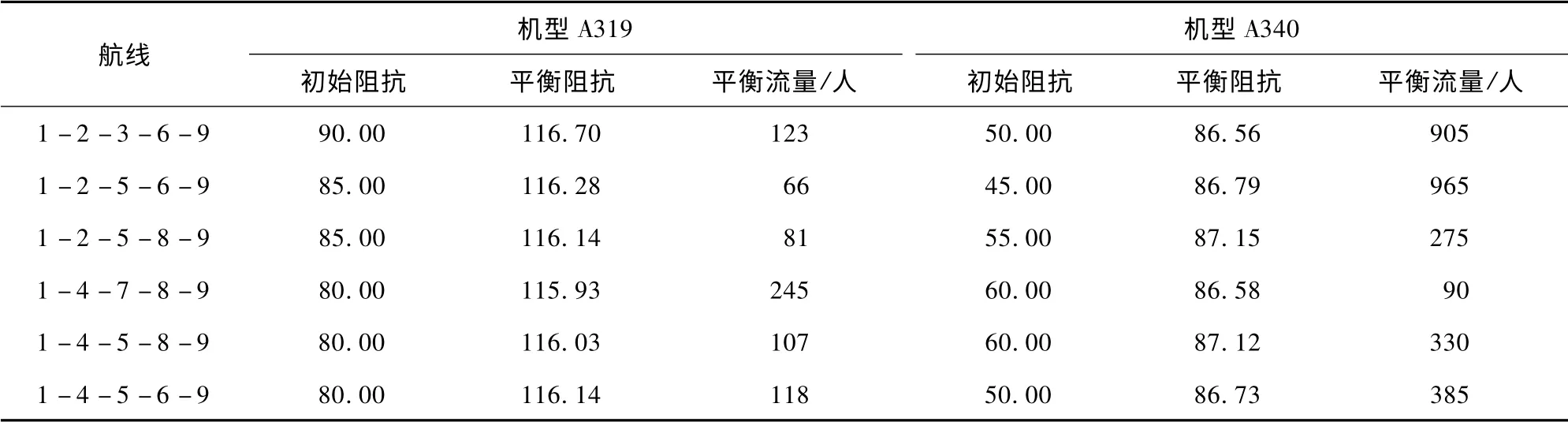
表4 阻抗与流量

4 结 语

本文研究了带延误的多机型航空战略投送兵力分配模型，通过算例对带中转延误的2 种机型的航空网络进行了兵力分配。但航空战略投送兵力分配模型非常复杂，除本文考虑的影响因素外，机场的保障能力、运力载客量单位和航线网络中的民航计划都将对整个投送任务带来影响，本文将在后续继续研究。

［1］ 陈森发，周晶. 城市交通均衡流分配的多模式模型及算法［J］.自动化学报，1993，19(2):190-196.

［2］ 任刚，王玮.交通规划中的动态路网及其模型研究［J］.公路交通科技，2002，19(6):108-111.

［3］ 杨佩昆，钱林波.交通分配中路段行程实践研究［J］.同济大学学报，1994，22(1):27-32.

［4］ 四兵锋，高自友.多模式的城市混合交通均衡配流模型及算法［J］.公路交通科技，1999，16(1):44-48.