基于多优先级动态规划算法的装备保障任务调度
2014-12-25刘亚东伊洪冰陈祥斌顾雪峰
刘亚东,伊洪冰,陈祥斌,顾雪峰,刘 波
(1.军事交通学院 装备保障系,天津300161;2.沈阳军区联勤部 军事交通运输部,沈阳110000;3.四川省军区 乐山预备役步兵旅,四川 乐山614200)
信息化条件下的作战,各种武器装备综合应用于战场,使得装备保障的难度和复杂性空前增大,装备保障已成为武器装备发挥效能和部队战斗力“再生”至关重要的因素和环节。这就需要完善以往“相对分散、各成体系”的装备保障体系,将装备保障作为一个大系统,将装备保障力量作为一个整体,最大限度对其进行统一配置与运用,实现高效的一体化保障。装备保障任务调度作为体系保障能力形成的基础,其目的在于在一定的时限内分配给具备一定保障能力的保障力量,使装备保障任务与装备保障力量之间进行合理的匹配,以获取完成装备保障任务流程的最佳效益[1]。
装备保障任务的调度问题,可以描述为给定一个任务集合和现有的装备保障力量单元的集合。任务集合确定了需要处理的所有装备保障任务,任务之间的执行顺序(包括任务的串行、并行以及交叉关系)、信息和数据流向,同时明确了装备保障任务处理的时间需求、装备保障力量单元需求等任务的基本特征;装备保障力量单元具备处理任务的功能,单元本身具备一定的基本属性(如运行速度、具备的功能能力、信息获取范围、数据或信息处理能力等),力量单元和任务之间通过任务的能力需求和单元的功能能力关联,以此进行力量单元—任务的分配。因而,力量单元到任务的分配通常以整个任务流程完成的时间最短或者以装备保障力量单元的充分利用为目标。
任务调度问题在农业、工业、信息科学等领域研究较多,在军事领域近几年来部分军事学者也开始借鉴一些理念与方法解决车辆运输调度、油料保障等问题[2]。然而在装备保障力量部署领域中,其部署主要依托作战需求及一定的约束条件,定性判断较多,人为经验成分多,对于在不确定的需求及复杂动态的环境变化下,如何有效解决装备保障任务与装备保障力量分配并行处理问题的研究较少[3]。论文借鉴多优先级动态规划算法,综合考虑各种因素,构建装备保障任务调度模型,旨在解决2 个问题:①得出装备保障任务的最优分配方案,即执行该任务的装备保障力量单元及执行时间;②确定任务的执行顺序,即确定完成整个装备保障任务最短时间。
1 装备保障任务调度模型的构建
装备保障任务调度的目标是缩短完成装备保障总任务的时间,提高完成装备保障任务的有效性,即分配合适的装备保障力量单元或装备保障力量单元的编组到正确的区域去执行合理的任务。具体地说,就是在满足装备保障任务力量需求的情况下,提高装备保障力量单元的利用率,缩短完成装备保障任务过程的时间。
1.1 条件约束
一般而言,某项装备保障任务的处理需要具备处理这一任务的所有条件。假设某装备保障任务由装备保障力量单元来完成,则需要具备如下条件。
(1)假设装备保障力量单元的数量足够、功能齐全,能够完成整个装备保障任务。
(2)假设在某一任务之前的所有任务都已处理完毕。
(3)分配到某任务的所有装备保障力量单元已在保障任务区域集结完毕。
(4)1 个装备保障力量单元每次只能完成1 个任务,且装备保障力量单元的能力不小于保障任务的需求量[4]。
1.2 决策变量
假设装备保障力量单元与装备保障任务间分配变量为wim,分配给保障力量单元Um任务ti时,wim=1,否则wim=0;保障力量单元在任务间转移变量为xijm,在保障力量单元Um处理任务ti后,又分配给其任务tj则xijm=1,不分配给任务则xijm=0。
当装备保障力量单元Um(1≤m≤K)和装备保障任务ti(1≤i≤N)之间存在分配关系时,装备保障力量单元Um被分配去执行装备保障任务ti有2种情况:①装备保障力量单元Um被首次使用,直接被分配处理任务ti,此时不存在转移变量,即转移变量xijm=0;②装备保障力量单元Um在处理完任务tj后被分配处理任务ti,此时存在转移变量,即转移变量xijm=1。
基于以上考虑,假设所有装备保障任务的起点为t1,在作战开始阶段,所有保障力量单元都在起始任务t1上,此时xiim=xjjm=0,则保障力量单元与任务分配变量wim和保障力量单元在任务间的转移变量xijm存在如下约束关系:
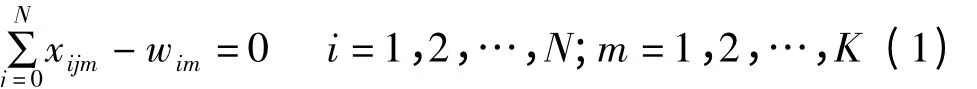
由于装备保障力量单元Um每次只能处理1个装备保障任务,在处理完任务ti后只能被分配完成某一个任务,而不能同时被分配完成多个任务,则
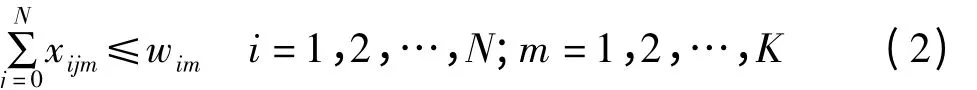
1.3 时间约束
假设任务顺序变量为aji,如果任务tj的处理必须在任务ti处理完后才能开始则为1,否则aji=0;假设时间变量为si,sj为处理任务ti的开始时间。由于任务间的顺序关系,任务ti的处理开始必须在其所有前导任务(pr(ti))处理完毕之后。因此,存在顺序关系的任务处理时间存在如下约束:式中D(ti)为装备保障任务的处理时间。
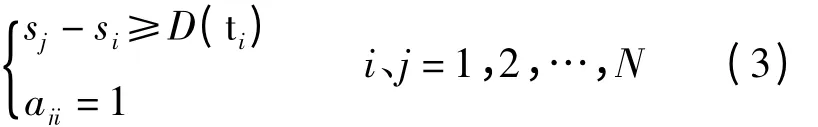
当装备保障力量单元Um(1≤m≤K)在处理完任务ti后被分配任务tj时,由于条件约束中已经假定,要求执行该装备保障任务的所有保障力量单元都到达任务区域,而现实中执行该任务的所有单元不可能同时到达,此时,先到达的保障力量单元需要等待。因此,保障力量单元Um开始处理装备保障任务ti的开始时间sj不小于保障力量单元到装备保障任务tj区域的时间,即

式中:dij为装备保障任务ti与任务tj之间的空间距离;vm为装备保障力量单元Um的机动速度。
其中
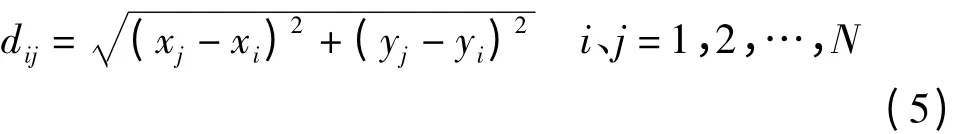
式中:(xi,yi)、(xj,yj)分别为装备保障任务ti与装备保障任务tj的地理位置。
综合式(3)和式(4),记Y'为所有装备保障任务完成时间的上界,则装备保障力量单元在任务的分配以及任务间的顺序关系约束可描述为
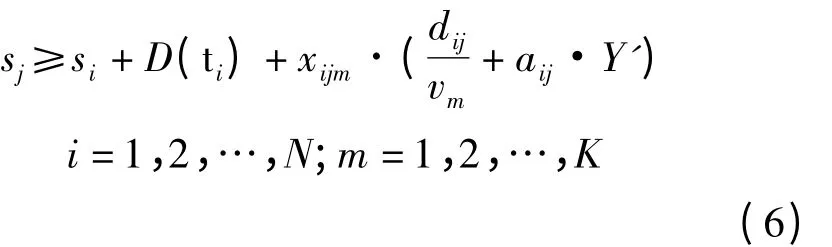
1.4 能力约束
成功处理装备保障任务ti的条件,是被分配处理这一任务的所有装备保障力量单元的能力不小于装备保障任务的需求Ri,即
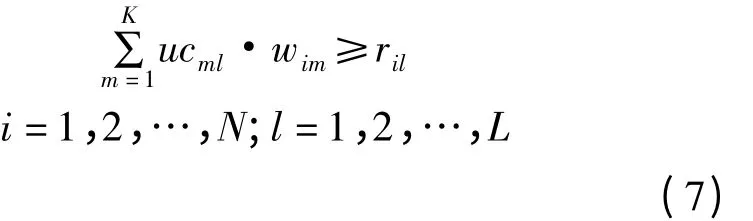
式中:L为装备保障力量单元的功能类型,如弹药保障、器材保障、维修保障、信息保障、防卫保障等。
令所有的装备保障任务全部完成时间为Y,则对任意装备保障任务处理的时间约束式(8)总能成立,即

综上所述,装备保障任务调度过程的数学模型可以描述为
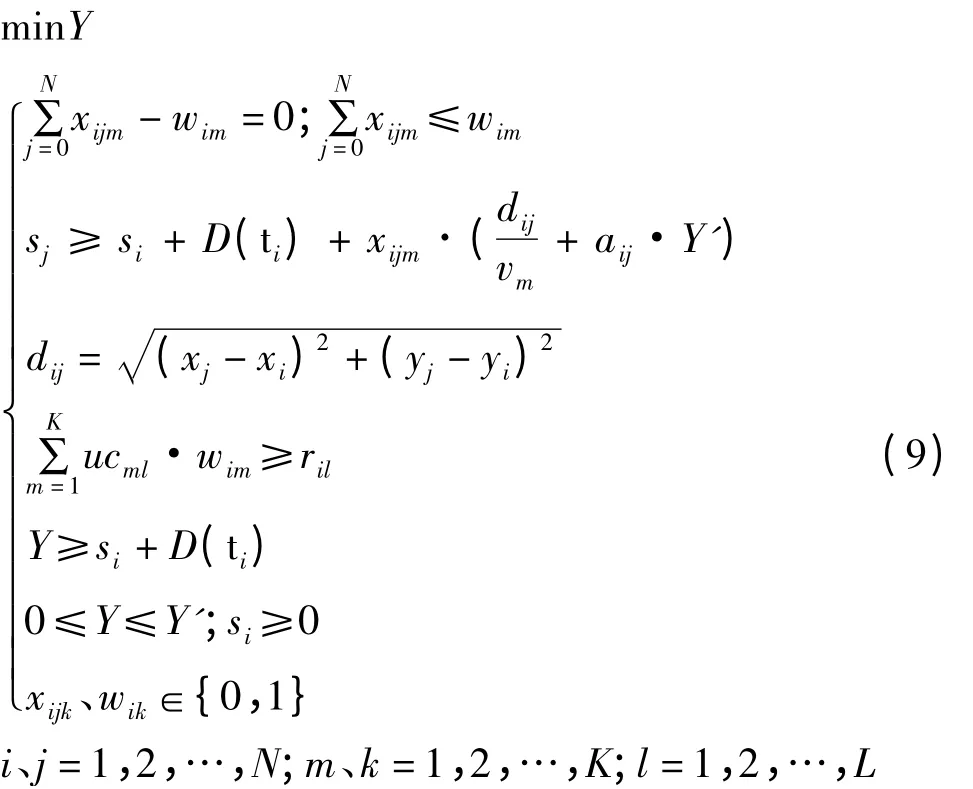
式中N、K、L分别为任务总数、装备保障力量单元数量和功能类型数量。
2 多优先级列表动态规划算法
2.1 相关概念的定义
在装备保障任务调度过程中,需要选择当前要执行的任务,确定任务对力量单元(或单元编组)的选择、力量单元对任务的选择。因此,在算法阐述之前需要定义装备保障任务分配的3 种优先权:任务优先权系数pr、任务选择力量单元的优先权tu和力量单元选择任务的优先权ut。
2.1.1 任务优先权系数
当某一任务之前所有任务都已处理完时,该任务便进入分配任务集rest中,在rest中首先选择任务优先权系数高的任务进行保障力量单元的分配,任务的优先权系数根据任务流程图中的任务序列依据算法来确定。本文通过采用加权长度算法来计算任务的优先权系数pr:
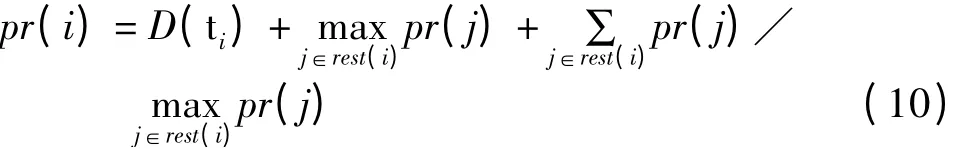
式中:rest(i)为装备保障任务之后待完成的任务集合;D(ti)为装备保障任务ti的完成时间。
2.1.2 任务选择保障力量单元的优先权
任务选择保障力量单元的目的是充分利用装备保障力量,保证完成任务的时间最短。充分利用力量单元就是要正好满足任务的资源需求,而任务的完成时间需要选择能在较短时间内到达任务区域进行处理任务的力量单元。因此,定义任务选择保障力量单元的时间优先系数tu1和保障力量单元功能矢量距离优先系数tu2分别为
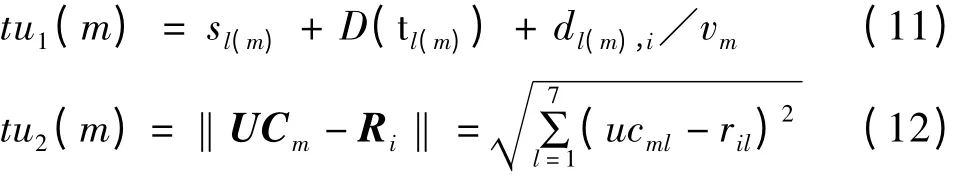
式中:tl(m)为力量单元Um最后处理的任务;UCm为力量单元Um的功能矢量;l为功能类型。
tu1是保障力量单元在处理完最后的任务后到达当前需要处理的任务区域的时间,tu2是保障力量单元的能力对任务需求的满足程度。因此,对于这2 个不同的系数,应通过tu1和tu2升序所建立的任务选择力量单元的优先级表来计算,即保障力量单元到达任务区域的时间早则优先考虑,保障力量单元能力满足任务需求矢量距离近则优先考虑。假设i、j分别代表优先系数tu1和tu2在各自序列中的位置,则任务选择保障力量单元的优先权tu为
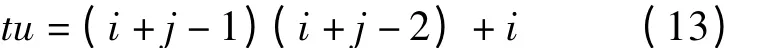
2.1.3 保障力量单元选择任务的优先权
保障力量单元选择任务的优先权ut,是指对未处理的任务进行优先级的排序。假设保障力量单元选择任务的时间优先系数为ut1,任务需求矢量距离优先系数为ut2。对某一个单元Um,其对任务选择的时间优先系数只需要考虑当前处理任务的区域到达等待处理的各任务间的距离。由此,2种优先系数可定义为
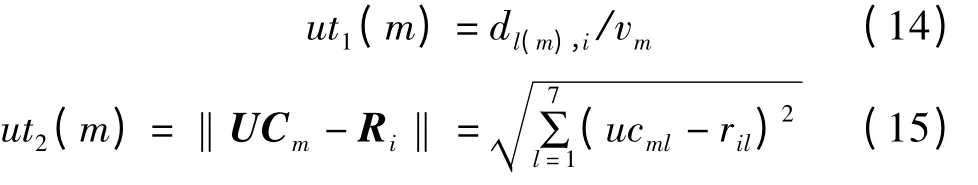
假设g、h分别为优先系数ut1和ut2在各自序列中的位置,则单元选择任务的优先权ut为
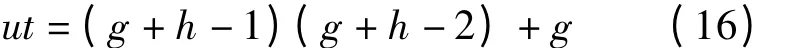
2.2 优先选择冲突的消除
由式(6)可知,单元选择任务的时间优先系数ut1在任务确定之后排序是不变的,其优先级列表是静态的,而任务选择单元的时间优先系数tu1是随着任务对单元的选择而不断变化的,其优先级列表是动态的。由于任务对单元的选择只考虑自身需求,而单元对任务的选择是对所有未处理任务的优选,这就存在着局部与全局的矛盾。因此,只要解决了任务选择单元的优先级问题(列表是动态的),即可解决2 种选择的冲突问题。在装备保障任务调度过程中,期望tu1优先级高的同时,也期望tu1优先级尽可能高。设单元对任务选择的静态优先级列表为SL,任务对单元选择的动态优先级列表为DL,Sut和Stu分别为utmi和tuim在SL、DL 中的排序,可用加权方法解决装备保障任务调度过程中的选择冲突问题。令PR(tu,ut)为2种选择优先权的协调,则加权公式为
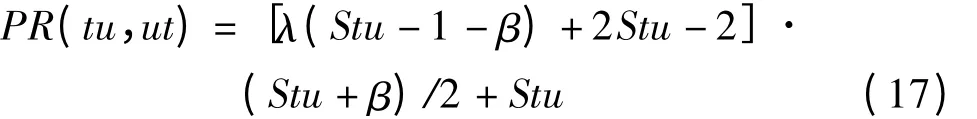
式中:λ 为权系数;β=Stu-2/λ。
2.3 算法流程
多优先级列表动态规划算法(multi-PRI list dynamic scheduling,MPLDS),主要包括3 个步骤:对选择的任务进行可分配性检查;从任务图中根据优先权选择要处理的任务;选择处理任务的最佳保障力量单元或单元编组(该部分包括任务对单元的选择、单元对任务的选择与2 种选择冲突的消除)。其流程如图1 所示。
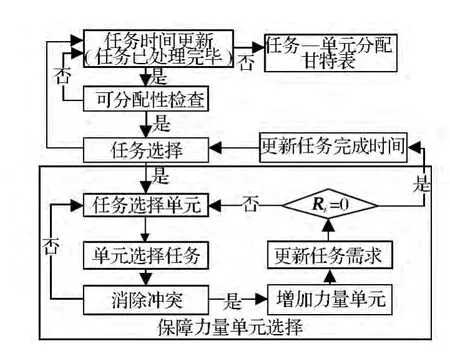
图1 MPLDS 算法流程
3 实例分析
选取某部队一次进攻演习过程中的某一阶段(即攻占敌方a1和b1高地所涉及的装备保障任务)来进行实例分析。按作战计划将总体的作战任务划分为13 个任务阶段,任务流程如图2 所示[5],任务内容见表1。

图2 任务流程
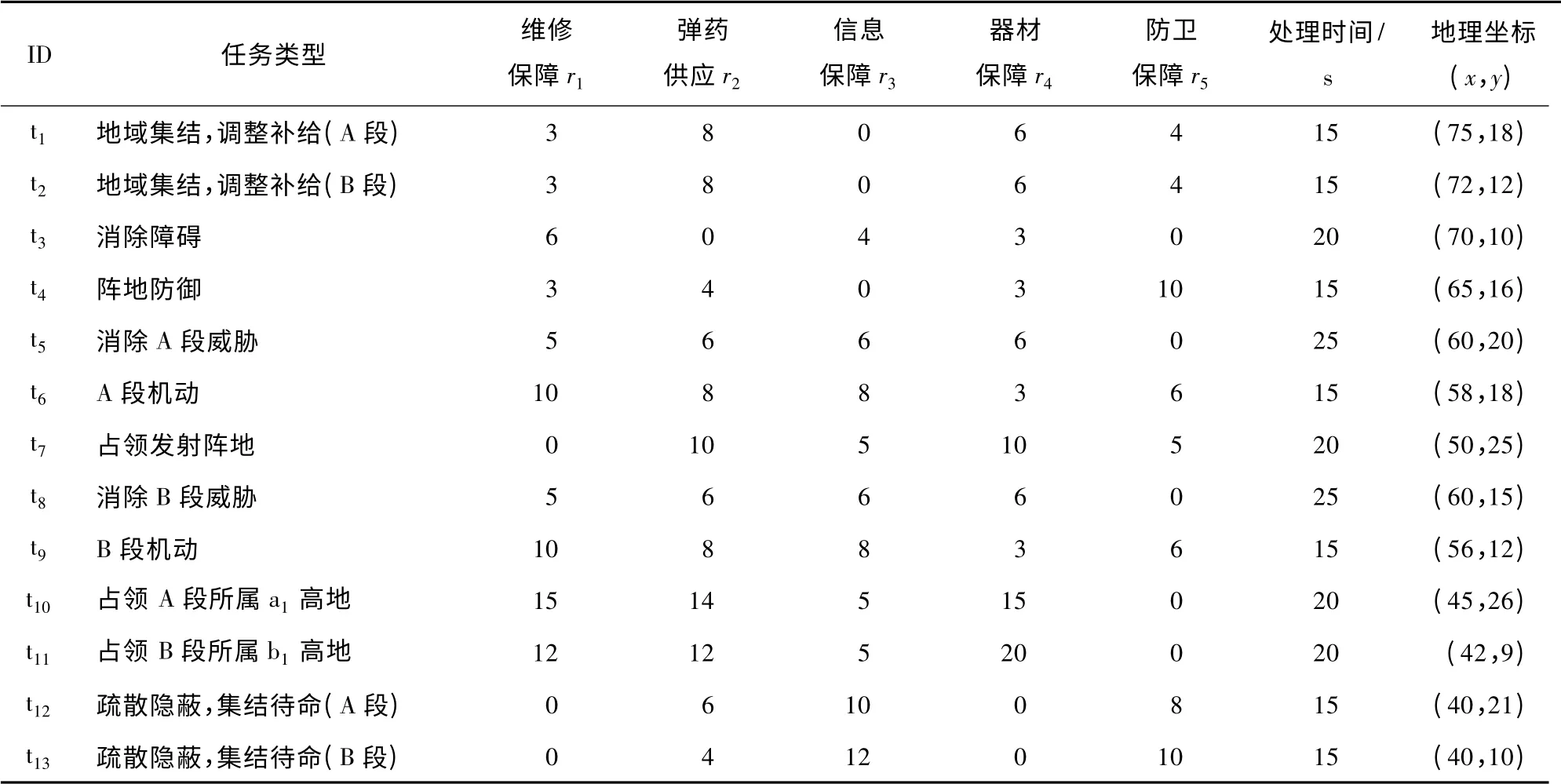
表1 任务属性及装备保障功能需求分析
由于在作战过程中需要对装备实施有效的维修保障、供应保障(弹药和器材)、信息保障及防卫保障,因此根据装备保障任务需要以及未来装备保障力量模块化的发展趋势,将装备保障力量单元划分为弹药保障力量单元、器材保障力量单元、信息保障力量单元、上装保障力量单元、底盘保障力量单元、防卫保障力量单元等7 类,具体属性见表2[6]。
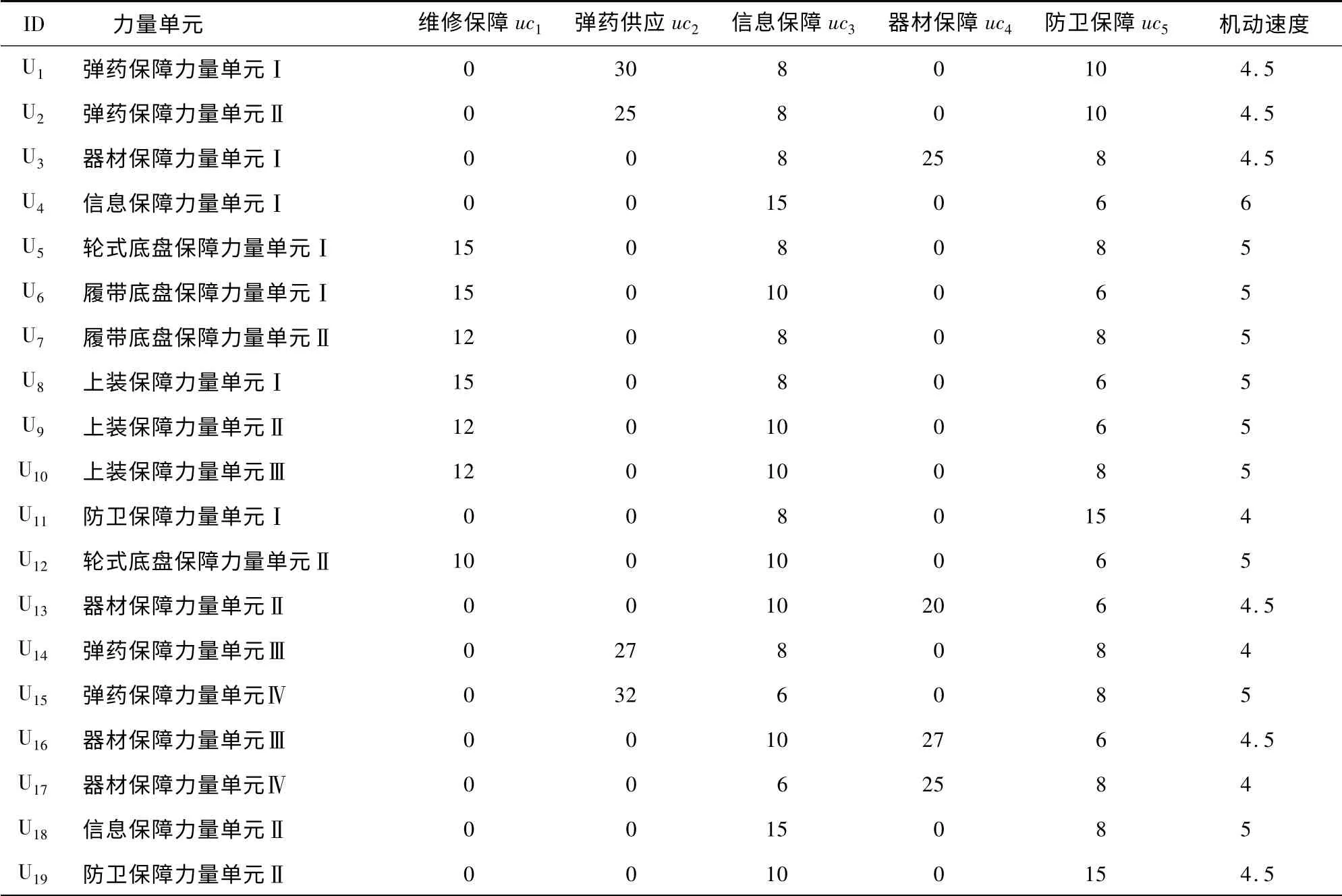
表2 装备保障力量单元属性
根据装备保障任务调度模型及MPLDS 算法,利用Matiab7.0 软件对算法进行编程,选取λ 为1和5 分别进行计算,结果如图3 所示。当λ 为1时,完成任务的总体时间为189.8 s,装备保障力量单元的协同总量为65;当λ 为5 时,完成任务的总体时间为100.6 s,装备保障力量单元的协同总量为43。

图3 MPLDS 求解结果甘特图
4 结 语
(1)通过力量单元对任务选择与任务对力量单元选择两者的结合,可以使装备保障任务调度的过程更加紧凑,任务的处理更为合理。一方面可以缩短完成总体任务的时间,为作战及保障的顺利实施提供了可靠的保证;另一方面可以充分利用装备保障资源,最大限度地利用和挖掘装备保障力量的保障能力,在提高保障资源利用率、保障力量协同保障能力的同时,促进保障效能的有效发挥。
(2)战时装备保障力量单元彼此之间需要加强协同,以促进体系保障能力的快速生成。通过2个结果对比分析可以发现,并不是保障力量单元协同越多,保障效能的发挥就越好,单元之间的协同过多反而会降低完成任务的效能,不必要的协同甚至会导致任务处理出错。因此,在平时的训练及演习过程中,要避免过分强调协同保障,当某个保障力量单元的能力能够胜任某一任务的需求时,就不用选择多个单元来完成这一任务。
(3)由于装备保障力量单元与任务的匹配需要多维变量测度,任务本身需要异构功能的装备保障力量单元的协同处理,并且要求装备保障力量单元能够处理多个任务,使得装备保障任务调度的复杂性大大增加。本文采用多优先级动态规划列表算法进行实例分析,解决了装备保障力量单元分配过程中存在的局部搜索和优先权函数的合理性问题,避免了力量单元在执行任务过程中不必要的协同。
[1] 任连生.基于信息系统体系作战能力概论[M]. 北京:军事科学出版社,2009:1.
[2] 崔浩,周庆忠,樊荣,等.一体化油料保障资源配置布局优化研究[J].军事物流,2010(8):139.
[3] 张春润,刘亚东. 基于复杂网络的装备保障力量体系保障研究[C]//中国兵工学会. 第二届质量、可靠性、风险、维修性、安全性国际学术会议论文集.2011:723-724.
[4] 吴秀鹏.装备保障力量模块化设计研究[D]. 石家庄:军械工程学院,2010:48-51.
[5] 张春润,刘亚东.装备保障需求开发方法研究[J].装甲兵工程学院学报,2012(3):14-18.
[6] 刘亚东,张春润,伊洪冰. 基于社会网络的装备保障组织网络拓扑结构研究[C] //中国兵工学会. 第二届质量、可靠性、风险、维修性、安全性国际学术会议论文集.2011:727.
