物理教学折射和折射成像研究

严开

在物理教学中，有些原理十分复杂和抽象，例如折射规律、折射成像的原理和像的位置变化等。借助简单直观的原理图，有助于降低思维的坡度，帮助学生理解;也有利于学生建立正确完整的物理图景，纠正前概念，启迪思维;更有利于激发学生的兴趣，立志学习物理。总之，千言万语说不清，实验一做就分明，图像一看更分清。

演示折射光线

在初中物理中，折射定律被定性地分为两部分来叙述：一部分是光由空气斜射入水（玻璃）中时偏折的情况，另一部分是光由水（玻璃）中斜射入空气中偏折的情况。学生脑海中一直存在着两个彼此独立的折射图景，这两个折射图景不时会纠缠不清，导致学生不能正确认识折射现象。笔者一直试图将这两部分折射现象归纳在一个物理原理图里面，方便学生对这两种情况进行比较，全面而深刻地掌握折射规律。

计算折射角和折射光线方程 如图1所示，横轴为两均匀介质空气和水的分界面位置，纵轴为法线位置，A点为光源，AO为入射光线，入射角为α，OB为折射光线，折射角为γ，O为入射点，空气的折射率n1=1，水的折射率为n2=1.3，由折射定律可知

折射角的大小为

若原点与入射点位置重合，则折射光线的方程为

即

利用GeoGebra演示折射光线 GeoGebra是自由且跨平台的动态数学软件，包含了几何、代数、表格、图形、统计和微积分，集中在一起使用的软件。由于其简洁、可深入交互，被越来越广泛地应用于物理日常教学中。

一是建立入射光线、入射点和入射角。如图2所示，在GeoGebra的绘图区横轴下绘制矩形表示介质水，向原点作线段AO表示入射光线，在纵轴上取点N，ON表示法线位置，度量∠NOA，GeoGebra默认该角用α表示。

二是绘制折射光线。在GeoGebra界面下方输入框中输入“Function[-tan（π/2-asin（sin（α）/1.3））x，0， +∞]”，这句命令的意思是在[0，+∞]内绘制的图像，即绘制出折射光线，如图3所示。如图4所示，在代数区中选择折射光线方程，右键单击选择”属性”菜单。如图5所示，在“高级”选项卡的“显示条件”下输入框中输入“0°<α<90°”，即显示当光线由空气自左向右斜射入水中时折射光线的位置。

三是绘制入射光线在四个区间里对应的折射光线。当入射光线在第二区间（0°<α<90°）即当光线由空气自左向右斜射入水中时，入射角为α，此时对应的折射光线为

当入射光线在第三区间（90°<α<180°）即当光线由水自左向右斜射入空气中时，入射角为（180°-α），此时对应的折射光线为

当入射光线在第四区间（180°<α<270°）即当光线由水自右向左斜射入空气中时，入射角为（α-180°），此时对应的折射光线为

当入射光线在第一区间（270°<α<360°）即当光线由空气自右向左斜射入水中时，入射角为（360°-α），此时对应的折射光线为

如上文所述，分别绘制各个区间的折射光线。以原点为起点，沿纵轴正方向作射线，显示的条件为（α=180°），即光由水垂直入射向空气中时，传播方向不发生改变;沿纵轴负方向作射线，显示的条件为（α=0°），即光由空气垂直入射向水中时，传播方向不发生改变。由此，如图6所示，在一个物理图景中完整地表达了折射规律，教师可以借助这个物理图景，解释各种基本的折射现象。

演示折射成像的步骤

当折射成像时，对于观察者来说，像的位置高于物体的实际位置，并且在观察者和物体之间。当问题的情境发生变化时，学生总是不能对此进行正确的判断，教师讲授起来也十分吃力，当真是“千言万语说不清，图像一画就分明”的问题。

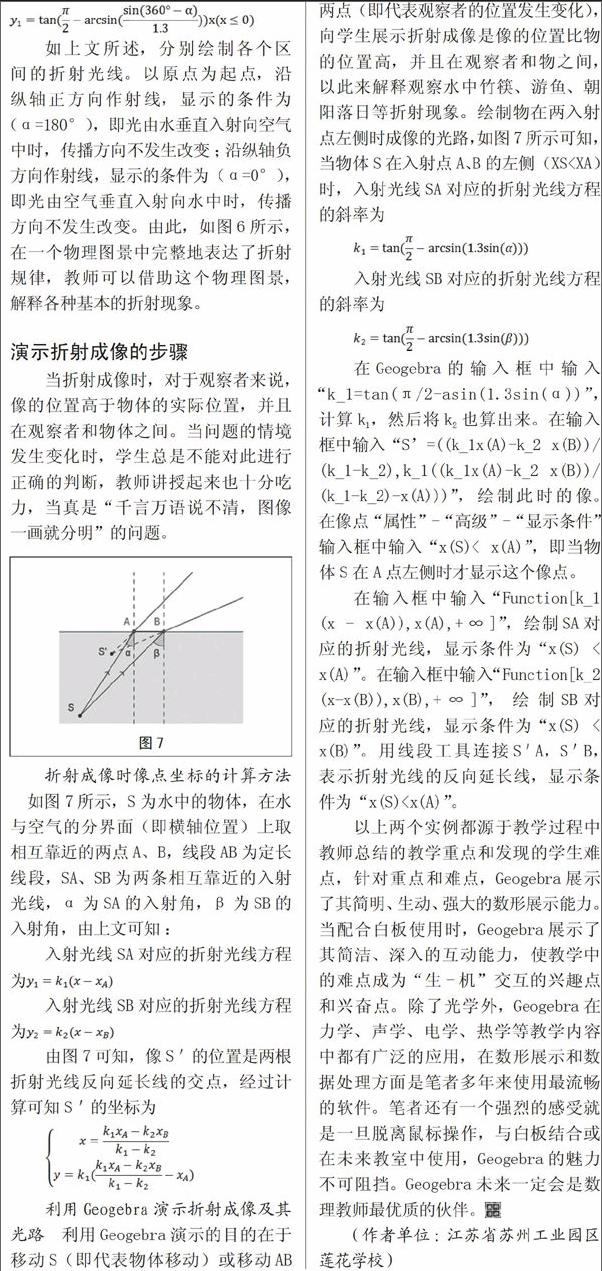
折射成像时像点坐标的计算方法 如图7所示，S为水中的物体，在水与空气的分界面（即横轴位置）上取相互靠近的两点A、B，线段AB为定长线段，SA、SB为两条相互靠近的入射光线，α为SA的入射角，β为SB的入射角，由上文可知：

入射光线SA对应的折射光线方程为

入射光线SB对应的折射光线方程为

由图7可知，像S'的位置是两根折射光线反向延长线的交点，经过计算可知S'的坐标为

利用Geogebra演示折射成像及其光路 利用Geogebra演示的目的在于移动S（即代表物体移动）或移动AB两点（即代表观察者的位置发生变化），向学生展示折射成像是像的位置比物的位置高，并且在观察者和物之间，以此来解释观察水中竹筷、游鱼、朝阳落日等折射现象。绘制物在两入射点左侧时成像的光路，如图7所示可知，当物体S在入射点A、B的左侧（XS

入射光线SB对应的折射光线方程的斜率为

在Geogebra的输入框中输入“k_1=tan（π/2-asin（1.3sin（α））”，计算k1，然后将k2也算出来。在输入框中输入“S=（（k_1x（A）-k_2 x（B））/（k_1-k_2），k_1（（k_1x（A）-k_2 x（B））/（k_1-k_2）-x（A）））”，绘制此时的像。在像点“属性”-“高级”-“显示条件”输入框中输入“x（S）< x（A）”，即当物体S在A点左侧时才显示这个像点。

在输入框中输入“Function[k_1 （x - x（A）），x（A），+∞]”，绘制SA对应的折射光线，显示条件为“x（S） < x（A）”。在输入框中输入“Function[k_2 （x-x（B）），x（B），+∞]”，绘制SB对应的折射光线，显示条件为“x（S） < x（B）”。用线段工具连接S'A，S'B，表示折射光线的反向延长线，显示条件为“x（S）

以上两个实例都源于教学过程中教师总结的教学重点和发现的学生难点，针对重点和难点，Geogebra展示了其简明、生动、强大的数形展示能力。当配合白板使用时，Geogebra展示了其简洁、深入的互动能力，使教学中的难点成为“生-机”交互的兴趣点和兴奋点。除了光学外，Geogebra在力学、声学、电学、热学等教学内容中都有广泛的应用，在数形展示和数据处理方面是笔者多年来使用最流畅的软件。笔者还有一个强烈的感受就是一旦脱离鼠标操作，与白板结合或在未来教室中使用，Geogebra的魅力不可阻挡。Geogebra未来一定会是数理教师最优质的伙伴。

（作者单位：江苏省苏州工业园区莲花学校）endprint