架空输电线任一点不对称短路时OPGW线路电流的分布研究

黎 鹏，崔 健，付 杰

(天津电力设计院，天津300400)

0 引言

由于光纤复合架空地线(OPGW)同时具有传统的地线保护输电线路的功能和光纤通信的功能，在架空输电线路上的应用也越来越普遍。OPGW 线的选型和校验显得非常重要。热校验便是其中一个重要指标，定量地计算出发生不对称短路故障时，OPGW 线上电流分量的值便是其中的关键。由于架空输电线路的可以分解成为由每两个杆塔之间档距形成的大规模的电力网络，要求解发生不对称故障时的短路电流，等价于求解由这些档距构成的网络［1～3］。其中涉及到线路的换位、杆塔的型号、杆塔的级数、杆塔接地电阻和线路两侧系统的参数等，通过这些参数求解等效电路［4，5］。注意到故障发生在杆塔处和故障发生在两杆塔之间时，电力网络明显的变化，使用合适的方法处理这些参数也是定量分析重要影响因素［10］。

本文采用网孔法对由OPGW 双地线系统架空输电线任一点不对称短路，包括不对称短路故障发生在杆塔处和两杆塔之间的情况下，短路电流分布情况进行量化计算和工程实例的验证，从而计算分析出OPGW 线系统中故障电流的分布特点，进而为OPGW 线的选型和校验提供参考。不对称故障包括单相接地故障、两相相间故障和两相接地故障。由于本文主要讨论的是故障后短路电流在OPGW 线上的分布，基于的前提是不对称故障中有接地短路电流存在的情况，所以文中指的不对称故障便针对性的为单相接地故障和两相接地故障，两相相间故障在此不作讨论。由于在OPGW 线上短路电流的来源于接地短路电流，虽然单相接地故障和两相接地故障虽故障类型不同，但计算方法是相同的。

1 发生单相接地故障时的数学模型

当线路上发生不对称短路情况时，可能存在两种类型位置上的故障:故障发生在杆塔上和故障发生在两杆塔之间。由于两种情况均有各自的特殊性，处理时的数学模型也是不相同的。在本文中，先讨论单相接地故障故障分别发生在杆塔处和两杆塔之间的时，在OPGW 线上的电流分布情况［6，7］。

1.1 故障发生在杆塔处

线路运行中，在杆塔处发生单相接地故障的模型如图1所示。图中，Rg为杆塔的接地电阻，Ea，Eb为每档距上两条OPGW 线上的感应电动势，Ia，Ib为每档距上两条OPGW 线上的电流，Za，Zb为每档距上两条OPGW 线上的自阻抗，M 为两条OPGW 线之间的互阻抗。r1，r2表示OPGW 线是否分段绝缘运行(在本文分析中，均认为r1，r2为0，非分段绝缘的运行方式)。k1，k2表示OPGW线是否逐塔接地运行［8］(在本文分析中，均认为k1，k2为0，逐塔接地运行)。OPGW 线发生单相接地故障时，通过上述模型得到等效电路。在短路的杆塔处，等效成一个电流源Id与杆塔的接地电阻并联［2］。

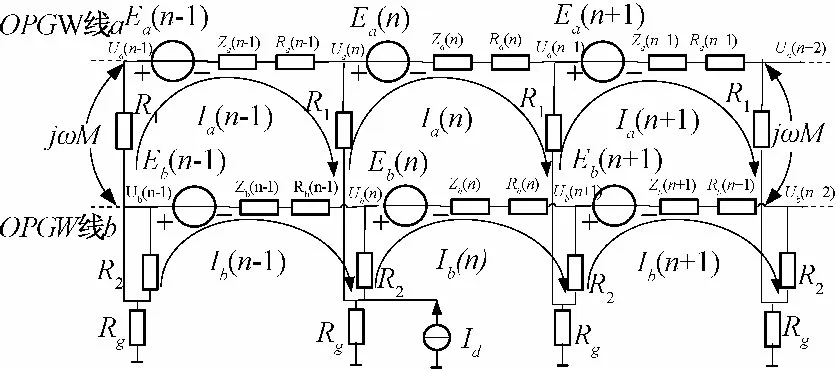
图1 故障发生在杆塔处时的等效电路图Fig.1 Equivalent circuit of shortcircuit at the tower

进一步将图1 中的电流源和接地电阻化简，等效成为一个电压源和电阻串联。

根据网孔法，列出图示第n-1 网孔所满足的方程:

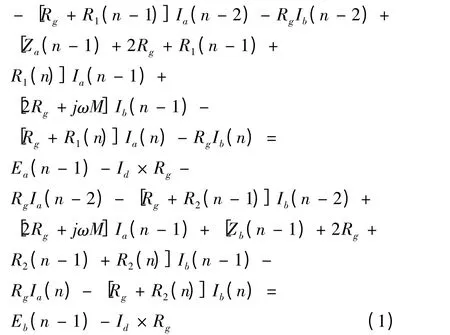
列出图示第n 网孔所满足的方程:

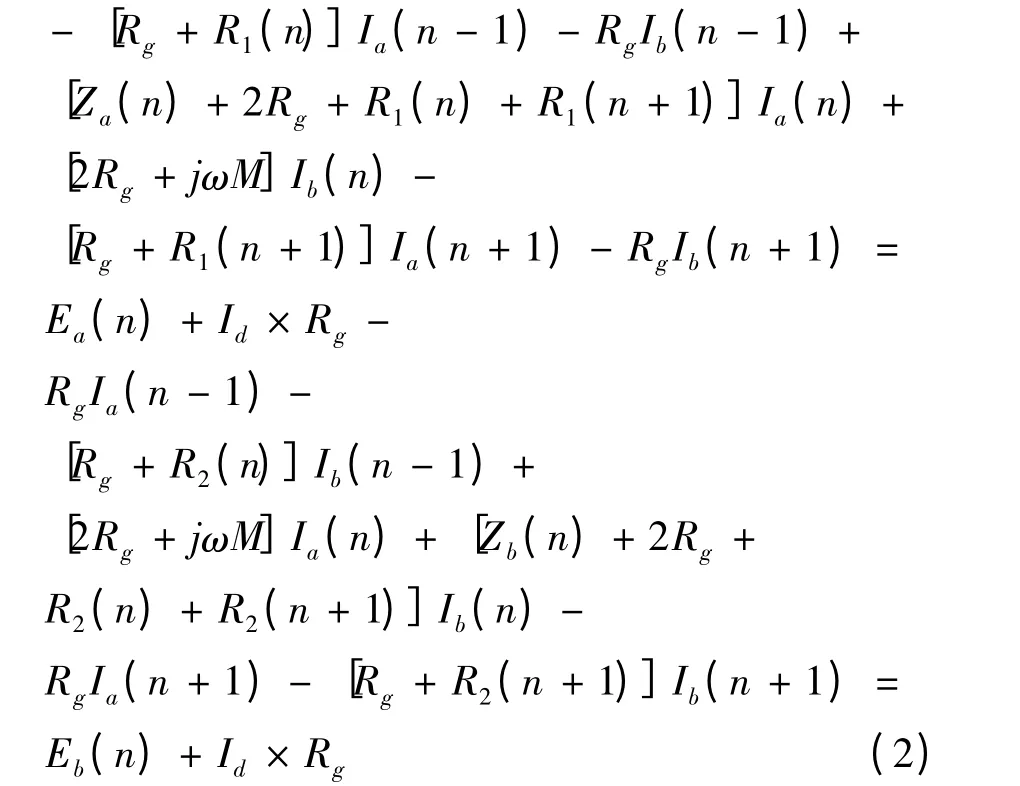
从第1 个网孔到第n 个网孔，就能写成如式(3)的矩阵的形式:

式中:Z 为阻抗矩阵;I 为两条OPGW 线上的电流矩阵;E 为两条OPGW 线上感应电动势矩阵。通过求解I，便能定量分析短路电流在OPGW 线上的分流情况。

1.2 故障发生在两杆塔之间

线路运行中，在两杆塔之间发生单相接地故障的模型如图2所示，在该模型中的所有的参数和图1 中的对应参数的意义完全相同。

根据短路后的电磁环境和实际电阻率［9］的综合考虑，确定短路电流的3 条分流路径的等效电阻值，随着在两塔之间的短路距离的变化，分流支路的短路电流的值也是在变化的，用拉格朗日差值法进行该阻值变化的曲线拟合。用Rf1和Rf3来模拟接地时到两侧杆塔处的地电阻，用Rf2来模拟接地电阻，同时短路电流Id从这3 个并联的电阻Rf1，Rf3和Rf2的节点注入。

图2 故障发生在两杆塔之间的等效电路图Fig.2 Equivalent circuit of shortcircuit between the towers

进一步将图2 中的电流源和接地电阻Rf2化简，等效成为一个电压源和电阻串联，如图3所示，同时在接地点多了两个网孔，假设其网孔电流If1和If2的参考方向如图2。

根据网孔法，列出图示第n-1 网孔所满足的方程:

列出图示第n 个网孔满足的方程:

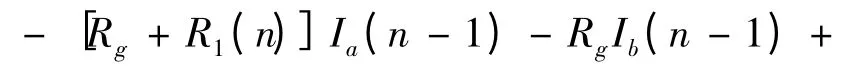
列出图示第n+1 个网孔满足的方程:

列出图示两个接地网孔满足的方程:

从第1 个网孔到第n 个网孔，就能写成如下的矩阵的形式:

式中:Z 为阻抗矩阵;I 为两条OPGW 线上的电流和短路点附加网孔中的电流If1，If2，E 为2 条OPGW 线上感应电动势矩阵。通过求解I，便能定量分析短路电流在OPGW 线上的分流情况，从而获得整个线路的电流分布。

2 发生两相接地故障时的数学模型

与前文中单相接地故障相比较，两相接地故障在计算OPGW 线上的短路电流分布所用方法相同。具体区别表现在两点:(1)短路电流数值不同，即公式中的Id需要重新计算;(2)输电线路上的短路电流不同，导致在OPGW 线上的感应电动势不同，及公式中的Ea和Eb需要重新计算。

计算两相接地短路情况下OPGW 线流过的电流，同样可以分为两相接地故障发生在杆塔处和两杆塔之间两种情况，分别如图1 和图2所示，计算公式仍使用公式(1)～(8)。需要注意的是，由于短路类型变化导致接地电流的变化，会影响到公式中具体参数值的变化，如OPGW 线上两杆塔之间的感应电动势Ea和Eb，进而影响到OPGW 线上电流的值。

总的来说，发生两相接地故障时，仍使用上文中的分析方法，故不再赘述。

3 实际工程算例

某双回输电系统的参数如下:电压等级220 kV;线路长度44 km;线路无换位;杆塔为120级，线路导线采用2 ×JL/G1A-630/45-45/7;地线采用2 根24 芯OPGW 线;OPGW 线承载截面积为154 mm2，直径为16.5 mm，直流电阻(20℃)为0.286 Ω/ km;OPGW 线逐塔接地，无分段绝缘方式运行，杆塔的接地电阻10 Ω。

在本文的计算中，考虑到了导线之间互阻抗的作用，过去在工程中分析故障电流的分布时简化处理了，并未考虑。

3.1 故障发生在杆塔处

采用上述的模型计算，不对称短路发生在杆塔上时，总短路电流为11.25 kA。OPGW 线上的各档电流的分布情况如图3所示。

不对称故障发生在杆塔上时，短路电流一部分经过杆塔入地，另一部分经过OPGW 流通。由于OPGW 线是逐塔接地方式，短路电流便在形成的网孔间分配，对靠近短路点的网孔影响较大，网孔电流变化较大。随着距离的增加，短路的影响也随之减小。所以出现了如图3所示的短路杆塔某一范围的OPGW 线档距上电流较大，两端电流较小的波形。

3.2 故障发生在两杆塔之间

采用上述的模型计算，不对称短路发生在杆塔之间时，总短路电流为11.25 kA。OPGW 线上的各档电流的分布情况如图4所示。

图3 短路发生在杆塔上时OPGW 上的电流Fig.3 Current on OPGW of shortcircuit at the tower

图4 短路发生在杆塔之间时OPGW 上的电流Fig.4 Current on OPGW of shortcircuit between towers

不对称故障发生在两杆塔之间时，短路电流一部分直接返回大地，一部分经过两杆塔返回大地，其余的部分通过两条OPGW 线流通。在发生故障的两杆塔之间的档距里，这个网孔中有着分别从两侧注入的短路电流，由于两侧注入的短路电流方向相反，造成该网孔中流通的电流值较小。在与此网孔相邻的网孔中，短路电流分别向两侧流通。随着距离的增加，影响也越来越小，因此出现如图4 中所示的电流波形。

可见，两种情况下OPGW 线中电流分配都是比较合理的，短路故障发生在杆塔处时，经过杆塔到两条OPGW 线上分流明显较大;短路故障发生在杆塔之间时，经过大地直接返回的电流较大，导致经过两条OPGW 线上的分流明显较小。

3.3 故障点在线路上的变化

假设从线路的始端到末端，随着故障点不断的变化，进一步来分析OPGW 线上的电流分布情况。

如图5所示，可以看到在逐级杆塔发生不对称故障后，OPGW 线的两杆塔之间线路上的电流的最大值的整体的变化趋势在第一级和最后一级杆塔上发生故障时的OPGW 线上的电流最大值是各级杆塔处发生故障的最大值中较大的，随着故障杆塔从第1 级到线路中间的推进，OPGW 线上的最大电流是逐渐减小的;随着故障杆塔从线路中间到最后一级杆塔的推进，OPGW 线上的最大电流时逐渐增大的，得到的是一个比较光滑的曲线。

如图6所示，可以看到在沿着线路发生不对称故障后，OPGW 线的两杆塔之间线路上的电流的最大值的整体的变化趋势是这样的，在靠近线路首端和尾端位置处发生故障的电流最大值是较大的，随着沿着线路，短路点的不断推进到线路中部时，OPGW 线上的最大电流是逐渐减小的;短路点从线路中部到尾端推进时，OPGW 线上的最大电流时逐渐增大的，得到的是一个锯齿状的曲线。

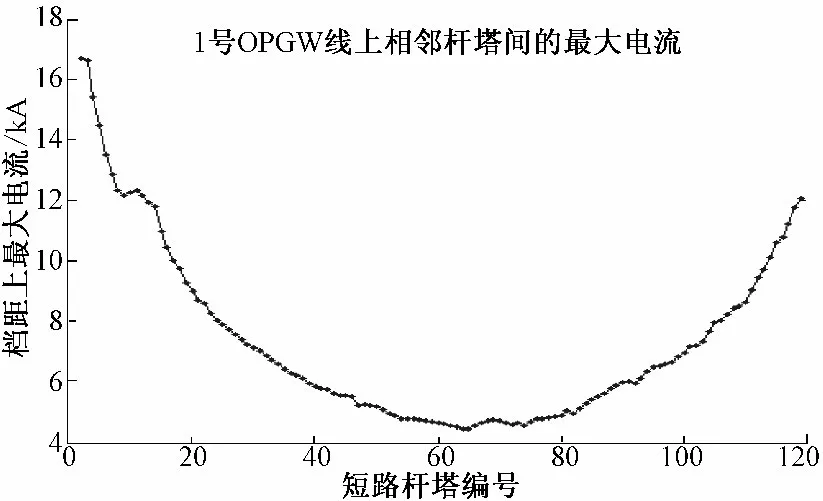
图5 线路逐塔短路时OPGW 线Fig.5 Current on OPGW of shortcircuit by tower

故障发生在杆塔上时的短路电流流经OPGW线上是最大的，所以上述的在OPGW 线上的电流波形便呈现出包络线的情形。

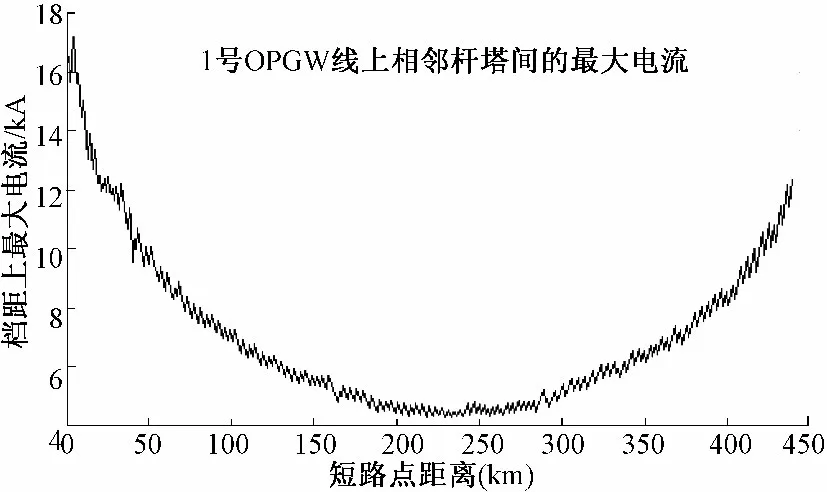
图6 线路逐点短路时OPGW 线Fig.6 Current on OPGW of shortcircuit by point

4 结论

本文的研究目的是利用网孔法对发生不对称短路故障时，架空输电线路每档距构成的电力网络的求解，得到双OPGW 线上的短路电流的定量的分布情况。详细地将故障分为发生在杆塔上的不对称短路和发生在两杆塔之间的不对称短路进行分析，计算结果表明，短路故障对靠近短路点杆塔的影响较大。得到故障发生在杆塔上时，流经OPGW 线上的电流要比故障发生在两杆塔之间时流经OPGW 线上的电流大。文中讨论的短路故障情况已比较详细，更复杂的OPGW 系统分析还须借助合适的软件进行分析，本文不再展开讨论。

［1］许正涛.OPGW 及其分流线的短路返回电流计算和选型校验［J］.中南七省(区)电力系统专业委员会第二十二届联合学术年会论文集，2007.

［2］许高雄，赵大平，戚力彦，等.OPGW 与普通地线构成的双地线系统中单相短路电流分流的计算［J］.电网技术，2011，35 (1):229-232.

［3］杜天苍，张尧，夏文波.利用短路电流热效应的OPGW 分流地线选型［J］.高电压技术，2007，33(9):110-114.

［4］邹军，袁建生，周宇坤，等.统一广义双侧消去法与架空线路-地下电缆混合输电系统故障电流分布的计算［J］.中国电机工程学报，2002，22 (10):112-115.

［5］赵科，邹军.复合光缆地线故障暂态电流和电压分布计算与分析［J］.高电压技术，2009，35 (10):2481-2485.

［6］李宝聚，周浩.1 000 kV 同塔双回线路感应电压和电流的计算分析［J］.电网技术，2011，35 (3):14-19.

［7］王宇，王建国，彭向阳，等.220kV 同塔双回输电线路架空地线感应电流与电能损耗［J］.高压电器，2013，49 (005):31-38.

［8］吴田，胡毅，刘凯，等.复合光纤架空地线在不同接地方式下的放电路径选择特性［J］.高电压技术，2012，38 (004):878-884.

［9］周晓虎，周秧.多层水平分层土壤电阻率模型［J］.现代电力，2007，24 (2):48-51.

［10］赵志斌，李琳.电力线路架空地线分流电流的计算［J］.华北电力大学学报(自然科学版)，2002，29(4):5-7.