基于灰色马尔科夫链的用电量预测模型分析及应用研究

唐 慧，唐 艳

(1.国网南京供电公司，江苏南京210000;2.中国水电工程顾问集团有限公司，北京100120)

0 引言

精确的用电量预测对电力系统的生产经营、规划建设等具有重要意义，能为电力企业制定生产经营目标与发展规划提供一定的依据，是电力企业制定配售电计划、经营战略和策略的基础［1］。由于用电量受到经济发展、产业结构、居民收入水平、国家政策诸多因素的影响，这些因素的随机性和关联性变化大，导致确保用电量的准确性比较困难［2］。电量的消费受到经济发展、产业结构、居民收入水平、气候、国家政策等诸多因素的影响，是一个灰色系统，适合用灰色模型描述［3］。GM(1，1)模型是最常用的一种灰色系统模型［4］，但由于GM(1，1)模型是一个指数函数，比较适合用电量增长较慢的情况，而实际用电量很难严格按指数规律变化，导致进行长期预测时，增长率过快，预测精度变低，因此GM(1，1)模型在实际应用中受到一定的限制［5，6］。马尔可夫预测是应用概率论中马尔可夫链(Markov chain)的理论和方法来研究分析时间序列的变化规律，并由此预测其未来变化趋势的一种预测方法［7，8］。本文将灰色预测和马尔科夫预测相结合，在GM(1，1)模型的基础上利用马尔科夫模型对预测误差进行调整，方法科学合理实用。

1 灰色预测模型的建立

GM(1，n)模型表示对n 个变量用一阶微分方程建立的灰色模型，主要用于终端能源和若干个影响变量之间关系的预测。

设有x1，x2，…，xn等n 个变量，对应有n 个历史数据组成的数列［5，6］，即

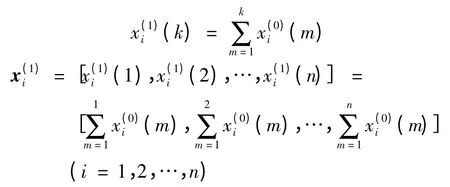
类似GM(1，1)模型，构造一阶线性微分方程为

这是一阶n 个变量的微分方程模型，故记GM(1，n)。记上述方程的参数列为，有。则按最小二乘法可求出来，其算式为

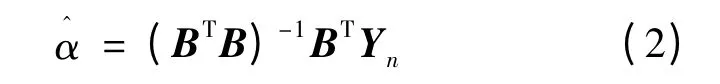
式中:

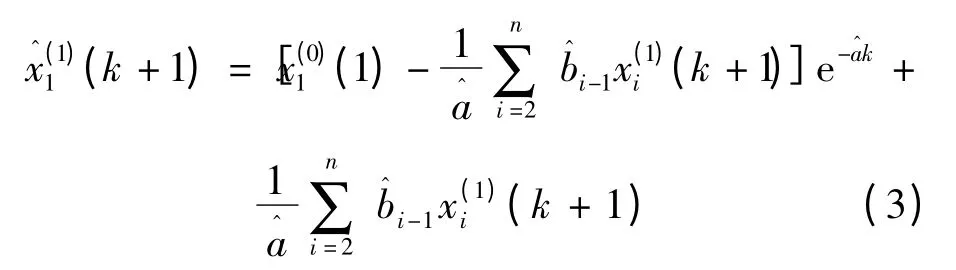
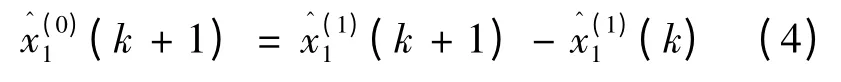
2 马尔科夫预测模型

马尔可夫预测是应用概率论中马尔可夫链(Markov chain)的理论和方法来研究分析时间序列的变化规律，并由此预测其未来变化趋势的一种预测方法。这种方法已在市场预测分析和市场管理决策中得到广泛应用，近年来逐步被应用于经济预测、能源规划、卫生管理事业等领域［7，8］。

设系统初始状态的概率向量为:S(0)=)，其中各元素表示处于状态i 的初始状态概率。若经过k 步转移后处于j 状态，切普曼—科尔莫戈罗夫(Chapman-Kolmogorov)方程可得到j 时刻的状态量:

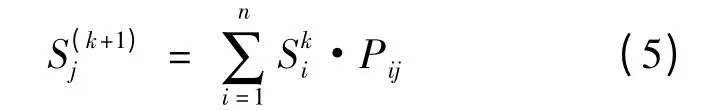
公式(5)就是所建立的马尔可夫预测模型，写成向量形式为

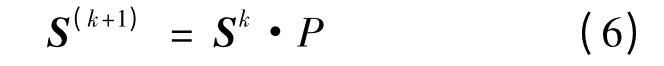
由递推关系可得到:

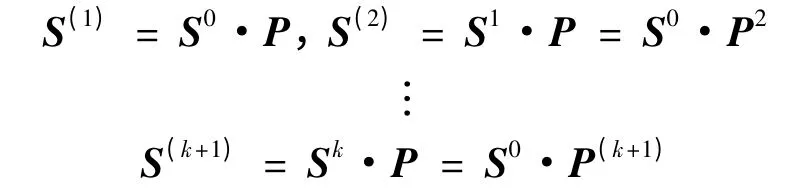
在应用马尔可夫矩阵进行调整时，最常用的是一步转移概率矩阵。在转移概率矩阵基本不变的条件下，随着时间的推移，认为系统将出现平衡状态，即系统中各状态的概率保持不变。此时有S(k+1)= Sk，将其写成矩阵形式。

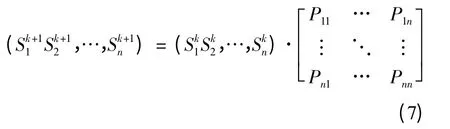
在计算得出一步转移概率矩阵的基础上，可以进一步得出系统的平衡状态，从而确定稳定情况下系统各状态的概率。

3 案例分析

应用灰色系统马尔可夫最优预测模型的具体步骤为:首先利用灰色预测对电力负荷进行初步预测，然后根据误差等级划分误差等级状态;根据状态确定一步转移概率矩阵;最后利用得出的一步转移概率矩阵和误差状态对预测进行后干预，得到更加精确的预测结果。

本文选取中国国家统计局网站上公布的电力生产量数据作为实例数据进行测算，收集从2003年到2012年10年的数据建立原始数据表(见表1)。

表1 2003～2012年全国供电量Tab.1 Power supply of China from 2003 to 2012

对预测结果和实际值的相对误差的百分数进行状态划分，由于相对误差均大于0，因此，选取正的区间作为误差转移矩阵划分的依据，建立马尔可夫转移矩阵，由于数据量比较少，所以划分状态区间以5 %作为参考，即［0，0.05］作为第1 状态，(0.05，0.10］作为第二状态，以此类推。经计算，各年度所处的状态如表3所示。

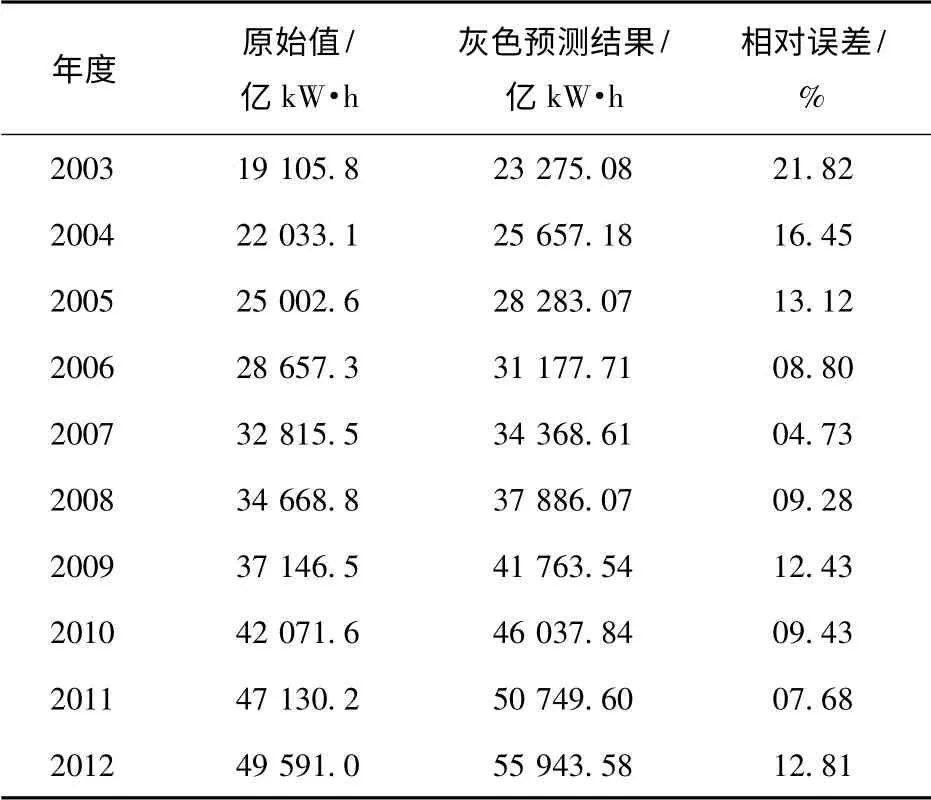
表2 灰色预测结果和相对误差Tab.2 Forecasting results of grey model and relative error

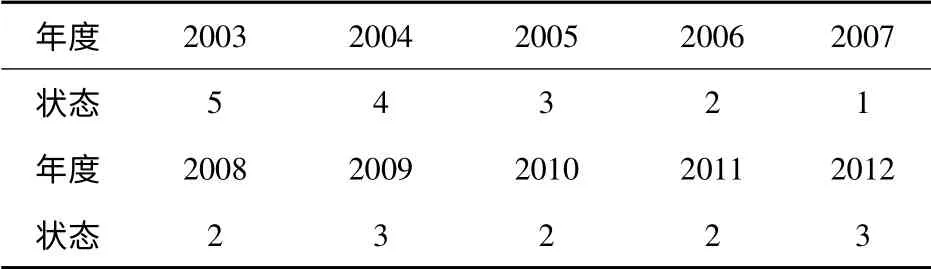
表3 各年所处状态表Tab.3 Status of every year

状态Ei经k 步转移到状态Ej的概率可以用Ei经k 步转移到状态Ej的次数代替，其中，表示Ei经k 步转移到状态Ej的次数，Ni表示状态Ei出现的总次数，可由下式计算。

以状态5 为例，状态5 转移后的状态只有状态4 一种，因此P51=0，P52=0，P53=0，P54=1，P55=0;以此类推，可以确定状态转移概率矩阵。

然后利用马尔可夫链的状态转移方程式对预测结果进行修正，利用相对误差所在状态确定修正误差率，其中kj= 0.05·j，以状态2 为例，0.05·(3－1)= 0.05 计算得到修正误差率后，利用计算预测结果。结果如表4所示。

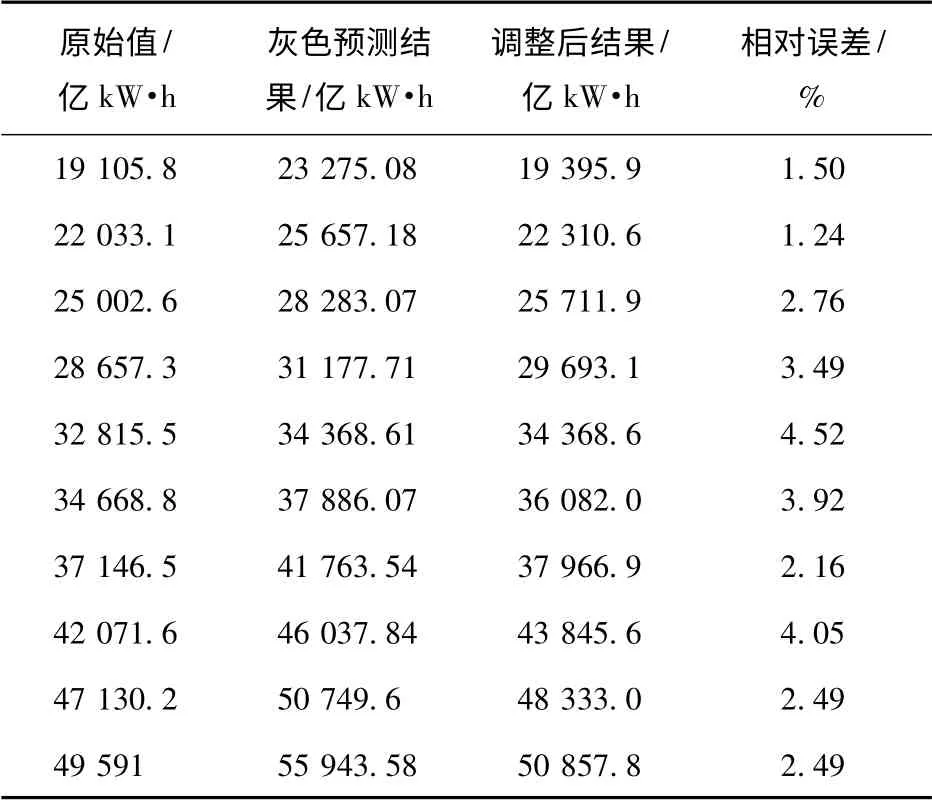
表4 经过马尔科夫矩阵调整后的预测结果Tab.4 Forecasting results of Markov adjustment

从预测结果可以看出，经过马尔可夫转移矩阵的调整，所有的相对误差均控制在5 %内，这样的预测结果比较实用，能够更加准确的指导电力规划。通过准确预测用电需求，我们可以合理安排电厂生产以及电建项目，不断提高电力企业的技术水平及运行管理水平，保证发、供电质量，提高发、供电的安全性、可靠性、经济性，增强电力企业的经济实力和市场竞争能力。

4 结论

通过灰色模型用电量预测并且利用马尔科夫进行误差调整，能够在保证误差精度要求的情况下准确预测用电需求，有助于合理安排电厂生产以及电建项目，不断提高电力企业的技术水平及运行管理水平，保证发、供电质量，提高发、供电的安全性、可靠性、经济性，增强电力企业的经济实力和市场竞争能力，为我国及地方电力产业持续快速健康发展提供技术保障。

［1］侯利强，杨善林，王晓佳.基于缓冲修正的样条灰色模型的长期负荷预测［J］.系统仿真学报，2013，25 (1):1－5.

［2］李伟，闫宁，张振刚.基于粗糙集的混合支持向量机长期电力负荷预测研究［J］.电力系统保护与控制，2010，38 (13):31－34.

［3］牛东晓，曹树华，卢建昌.电力负荷预测技术及其应用［M］.北京:中国电力出版社，1998.

［4］王大鹏，汪秉文.基于变权缓冲灰色模型的中长期负荷预测［J］.电网技术，2013，37 (1):167－171.

［5］焦润海，苏辰隽，林碧英，等.基于气象信息因素修正的灰色短期负荷预测模型［J］.电网技术，2013，37 (3):720－725.

［6］李泓泽，郭森，王宝.基于最小二乘组合灰色模型的中长期电力负荷预测［J］.水电能源科学，2012，30 (8):187－189.

［7］刘纯，吕振华，黄越辉，等.长时间尺度风电出力时间序列建模新方法研究［J］.电力系统保护与控制，2013，41 (1):7－13.

［8］严太华，陈明玉.基于马尔科夫切换模型的上证指数周收益率时间序列分析［J］.中国管理科学，2009，17 (6):33－38.

［9］何俊，王传丽.基于改进GM (1，1)的CPI 灰色预测模型(J).商业研究，2009，(3):32.