基于因子交互分析的热电厂经济性优化研究

付殿峥，黄国和

(华北电力大学区域能源系统优化教育部重点实验室，北京102206)

0 引言

随着现代城市住宅区域的逐步扩大，以热电厂为主要热源并结合调峰锅炉房为辅助热源的多热源集中供热系统逐渐成为我国北方大型城市采暖期供暖的主要形式。集中供热系统能够集中能源资源，提高一次性能源的综合利用率，与分散供热相比可以节省燃料和管理人员，便于消烟除尘，同时还可显著地减少对大气环境的污染［1］。热化系数，作为衡量热电厂经济性的重要宏观指标，对采暖期热电厂经济性、节能降耗、上网发电、调峰乃至设备运行寿命都会产生深远影响。在以热定电的原则下，不合理的热化系数由于不能充分利用供热机组的供热能力，会造成燃料浪费，环境污染，供热成本增加，并使得发电上网达不到电网调度需求。近些年来，学者对热化系数的研究，着重于热化系数与其他影响参数间的互动研究，如热化系数与燃料节约量，热化系数对供热成本的影响［2～4］，或者通过人为设定热化系数值来进行供热和供电分析［5］，但国内外对于供热负荷预测与热化系数两者之间的关联性研究尚属空白，即缺少基于供热负荷预测来进行热化系数优化方面的研究。同时，由于热电厂不仅作为主热源进行供热，还承担着发电上网、调峰等任务，因此合理调整供热与发电二者之间的关系使燃料消耗成本最小也显得尤为重要。与之相关的参数如热电厂供热、发电煤耗率，煤质波动，最低发电功率和热电联产中的热电比等都会由于不确定因素产生波动［6，7］，影响系统煤炭消耗量的确定，进而影响煤炭供应成本。因此，本文利用我国北方某大型城市采暖期的多热源供热系统供热案例进行研究，首先将基于相关参数收集，利用无因次综合公式法对采暖期供热负荷和供热量进行预测，其后结合相关法规政策及实际情况，建立热电厂热化系数优化模型，最后利用建立的非线性优化模型，兼顾考虑模型系统中的不确定参数因子，进一步分析不同因子参数间的交互作用对系统目标函数(煤炭供应成本)的影响［8，9］。

1 模型建立

多热源供热系统的热化系数可定义为作为主热源的热电厂承担的基本负荷所占供暖设计负荷的比例。区域锅炉房作为系统中的调峰热源，是当供热系统负荷超过基本热负荷时，用来辅助热电厂以提供尖峰负荷的辅助热源。选择合理的热化系数是降低供热成本，提高集中供热经济效益，兼顾发电及节能降耗的重要途径之一。因此热化系数对系统的供热、发电综合经济效益发挥有着很大影响［4］。

1.1 主辅热源供热量的确定

本文采用无因次综合公式法来绘制供暖热负荷延续时间图，可以以此预测采暖用户的热负荷和供热量［10］。在计算热负荷过程中，只要已知当地的采暖时间hzh(h)、当地采暖室外计算温度t′w(℃)和采暖期室外平均温度tp，j(℃)即可。但计算各热源实际供热量，除了依据供暖热负荷延续时间图外，还需要热化系数等其它参数。主、辅热源供热量表达式分别为

热电厂(主热源)供热量:

调峰锅炉房(辅助热源)供热量:

式(1)和(2)中:Q′n，Qnn，Qna和Qnb分别为采暖设计热负荷，(GJ·h－1);采暖期总供热量，GJ;主热源供热量，GJ;调峰热源供热量，GJ;a，hzh和ha分别为热化系数，p.u.;采暖期总数，h;热化系数为a时的采暖期延续数，h;b 和β0分别为模型相关指数值和温度修正系数，p.u.，可通过无因次综合公式法计算得出。本文在计算供热量时，在原供热量计算公式基础上，考虑到实际供热负荷和延续h数二者之间具有较强的线性特征，将借助线性回归分析确定a 与ha之间的线性关系的方法求得供热量，从而减少供热量计算所需参数，简化供热量计算，具体计算过程如下。

如图1所示，多边形SBDEFG面积为采暖期主热源的供热量，梯形SDAIE面积为调峰热源的供热量。

对供热负荷和延续h 进行线性回归分析后，可以得到:

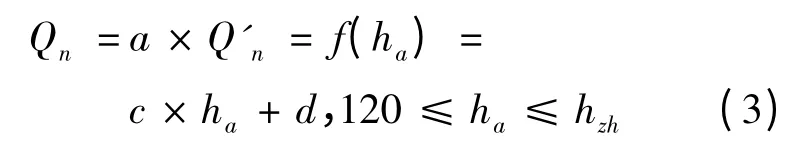
其后通过计算多边形SBDEFG面积和梯形SDAIE面积，得到主热源和调峰热源供热量表达式分别为

图1 线性回归下的供热负荷－延续时间图Fig.1 Linear regression-based heat load duration curve

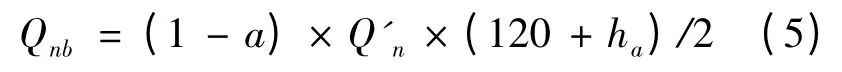
式(3)～(5)中:Qn为主热源(热电厂)设计供热负荷，(GJ·h－1);Qb为基础供热负荷，即室外温度为5 ℃时对应的供热负荷，(GJ·h－1);f(ha)为关于ha的一次线性函数;c 为自变量ha的一次项系数;d为常数项系数;ha可通过f(ha)的反函数计算得到。在已知供热延续h 图情况下，将以a 为自变量，ha为因变量的线性表达式带入式(4)和(5)中，即可得到Qna和Qnb关于a 的二次非线性表达式。此种供热量计算方法的可靠性验证见2.2 节。

1.2 热电厂热化系数优化模型建立

为确定最佳热化系数，该优化模型以多热源供热系统采暖期供热发电耗煤成本最小为目标函数，并辅以国家地方法规和机组实际情况为相关约束来建立优化模型。模型具体如下:

(1)目标函数为热电厂和调峰锅炉房供热发电耗煤成本最小:

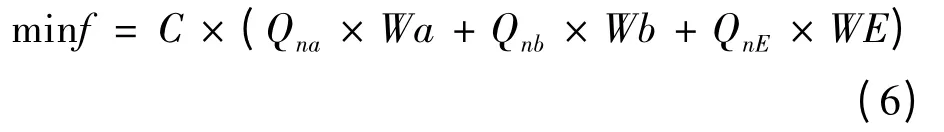
式中:C 为标煤单价，(元·t－1);Wa 为热电厂供热量的标煤耗率，(t·GJ－1);Wb 为调峰锅炉供热量的标煤耗率，(t·GJ－1);WE 为发电量的标煤耗率，t·(GW·h)－1;QnE为热电厂在以热定电原则下的发电量，(GW·h)。发电量QnE= Qna/(3 600 × η)。热电厂和调峰锅炉房供热量Qna，Qnb分别由式(4)和(5)得出，最终目标函数可化简为关于热化系数a 的二次表达式。

(2)根据《中华人民共和国节约能源法》和国家计划委员会、国家经济贸易委员会、电力工业部、建设部《关于发展热电联产的若干规定》要求以采暖供热负荷为主的热化系数宜控制在0.5～0.6 之间。因此:

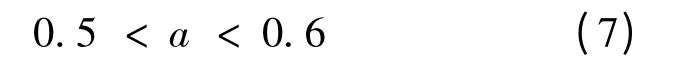
(3)根据地方实际节能环保需求，热电厂在设计热负荷下供热最低延续h 数不应少于:

HL ＜ha(ha可形成关于a 的线性表达式)(8)式中:HL 为主热源设计热负荷下供热限制延续时间，h。

(4)根据国家“以热定电”原则，按照地方发电和电网调峰需求，热电厂发电功率应稳定在一定区间:

式中:η 为热电比，p.u.;EL 为热电厂规定最低发电功率，MW;EU 为热电厂额定发电功率，MW。

综合(6)～(9)式，最终形成了以热化系数a为决策变量，多热源供热系统采暖期供热发电耗煤成本最小为目标函数的优化模型。

2 案例分析

2.1 研究区概述及供暖热负荷延续时间图绘制

本文以北方某大型城市的经济新区采暖期供热为案例进行分析。该市地处我国北方严寒地区，采暖期为5 个月左右。该经济新区尚处于建设初期阶段，供能形式上一直采用能耗高且环境污染严重的热电分供的形式。该区政府为改善新区的供能方式，已拆除多座分散小型供热锅炉房，并将与中国华能电力集团合作，拟在区内南部地区建立2 ×135 MW 抽汽式热电联产机组。该热电厂发电上网的同时，也将作为集中供暖主热源，形成以热电厂供热为主，兼顾供电，调峰锅炉房供热为辅的多热源供热系统。由该市2010年鉴可知，该区域内原4 个镇总人口数为18 万人，住宅主要为低层或多层住宅，人均住宅面积33 m2·人－1，单位住宅面积耗热量为64 W·m－2，由此可得到采暖用户所产生的最大热负荷为380.16 MW［11］。同时以该市1951～1980年30年的气象资料为基础，考虑气候变化对当地采暖期气温的实际影响，以0.1 ℃/10年的保守升温速率估计值对该地区的采暖期平均气温统计结果进行了外延［12］，统计出该市的采暖时间hzh、当地采暖室外计算温度t′w和采暖期室外平均温度tp，j分别为3 648 h，－19 ℃和－5.7 ℃，室内采暖设计温度tn为18 ℃，同时利用无因次综合公式计算出的各温度段下供暖热负荷延续时间(如表1所示)，由此绘制出供暖热负荷延续时间图，如图2所示。

表1 该市年供热负荷延续时间表Tab.1 Annual heating load duration hours

2.2 热化系数优化模型求解

图2 热负荷－延续h 数散点图Fig.2 Scatter plot of heat load and duration hours

由图2 供热负荷－延续h 数散点图可知，供热负荷与延续h 具有较好的线性趋势，得到二者间的线性回归方程为:Qn=1328.123－0.241×ha。其中，检验结果的判定系数R2为0.993，且方差分析以及系数的显著性检验结果均为显著，由此可进一步得出a 与ha间的线性关系式:

将公式(10)带入公式(4)和(5)中，即可得到热电厂和调峰供热房的供热量。为验证供热量计算公式(4)和(5)的准确性，将不同的a 值(0.513，0.621 和0.730)分别带入到两组供热量计算公式中，得到主热源供热量相对误差分别为0.08 %，0.26 %和0.09 %;调峰热源供热量相对误差为0.20 %，0.11 %和0.68 %。由此可知，所提出的供热量计算方法较为准确可靠。结合文献参考和实际情况［13］，得到模型内相关参数为:Wa=0.040 t·GJ－1，Wb =0.044 t·GJ－1，WE =330 t·(GW·h)－1，C=690 元·t－1，η =1.8，HL =2 200 h，EL = 110 MW，EU = 135 MW(按额定功率计算)。其后将ha关于a 的线性表达式和相关参数带入式(4)～(9)中，并进行求解，得到模型优化结果为:该多热源供热系统在采暖期最优煤耗成本为1.98 ×108元，热化系数为0.558，即为达到最佳煤炭供应成本，提高集中热电厂经济效益及节能减排的目的，多热源供热系统的热化系数值应调整为0.558。其中热电厂供热量为2.70 ×106GJ，调峰锅炉房供热量为6.46 ×105GJ。

2.3 不确定参数的交互作用分析

由于热电比对采暖期热电厂的上网发电－调峰有着重要影响，同时考虑到现实中其它一些关键参数波动导致的不确定性也会对采暖期煤炭供应成本产生影响，因此，本文将模型中与热电厂相关的重要参数潜在波动区间上下界视为不确定区间参数的高低水平(以区间数表示)，利用Zhou 等人［8，9］提出的非线性模型中区间参数交互作用分析法进行热电比与其它参数的交互作用分析(目标函数对参数共同变化的响应)，考虑的因子参数除热电比(η =［1.6，1.8］)外，还包括热电厂供热煤耗率(Wa=［0.040，0.042］t·GJ－1)、发电煤耗率(WE=［330，340］t·(GW·h)－1以及最低发电功率(EL =［105，110］MW)等(由于最高发电功率为热电厂的额定发电功率，同时标煤价格与系统成本有着较为显著的相关关系，在此对以上二因子不予以讨论)。

图3 为热电比与发电煤耗率交互作用分析结果。由图3 可知，发电煤耗率无论处于较高或较低水平时，热电比水平的提高都会导致系统煤炭供应成本的下降(当发电煤耗率在低水平时，成本响应均值由2.017 ×108元降低到1.971 ×108元;当发电煤耗率在高水平时，成本响应均值由2.045 ×108元降低到1.999 ×108元)。这主要是由于热电比升高，发电量不变时，热电厂供热量增加，为满足总供热量需求，调峰锅炉房供热量随之降低，而调峰锅炉房单位供热量煤耗率又高于热电厂，因此系统总供热需煤量降低，发电量、需煤量维持不变，从而导致了煤炭总需求量降低，进而导致了煤炭供应成本下降;当热电比处于不同水平时，供热量和发电量均保持稳定，因而发电煤耗增加则会显著增加发电煤炭需求量，从而导致整个系统煤炭供应成本的增加。图4所示的为热电比与供热煤耗率交互作用分析结果。与热电比与发电煤耗率之间的交互作用结果相似，供热煤耗率无论处于何种水平，热电比水平的提高都会导致系统煤炭供应成本的降低，这主要由于热电比升高时，此时所得热化系数没有变化，即热电厂和调峰锅炉房供热量均保持不变，而相应发电量减少造成了系统煤炭总需求量降低，进而导致了煤炭供应成本下降;当热电比处于不同水平时，供热煤耗率的增加则会显著增加系统供热的煤炭需求，进而导致了煤炭供应成本的升高。由此可知，在煤耗率保持稳定情形下，热电比与系统采暖期煤炭供应成本呈负相关关系;当热电比保持稳定时，煤耗率的增加则会显著增加系统煤炭需求成本;当热电比处于高水平，热电厂发电/供热煤耗率处于低水平时，系统煤炭供应成本最小。

图3 热电比与发电煤耗率交互作用分析图Fig.3 Interaction plot of power generation coal consumption rate and heat-power ratio

图4 热电比与供热煤耗率交互作用分析图Fig.4 Interaction plot of heat-supply coal consumption rate and heat-power ratio

图5 为热电比与最低发电功率交互作用分析结果。当最低发电功率保持稳定时，热电比的升高会使系统煤炭供应成本下降。主要原因在于此种情况下，热电厂发电量保持稳定，热电厂供热量的提高会使供热总煤耗降低，进而导致了系统煤炭供应成本下降。当热电比处于高水平时(1.8)，最低发电功率的降低导致系统煤炭供应成本降低(成本响应均值由2.009 ×108元降低到1.961 ×108元)。主要原因为:最低发电功率降低造成了发电量减少，为保持热电比稳定不变，热电厂供热量需随之下降;同时，为满足采暖期总供热量需求，调峰锅炉房的供热量则相应增加，然而调峰锅炉房供热煤耗率要高于热电厂，最终导致了系统内供热需煤量增加，发电需煤量减少。由于发电和供热是两种不同品位的能量，生成二者所需的压力和温度也不尽相同。作为高品位的能量形式，要产生同样能量单位电能，与热能相比较，煤耗则要高出许多，因此，尽管供热量所需总煤耗量增加，发电煤耗量减少，但降低发电量所减少煤炭需求量比供热增加的煤炭需求量要多出许多，从而最终导致了总需煤量下降，系统煤炭供应成本降低。当热电比为1.6 时，由于此时在热化系数求解过程中，热化系数已经达到了优化模型可行解空间的下界(a=0.5)，因此，降低最低发电功率变化不会引起系统煤炭需求成本的变化。类似地，满负荷运行最低延续h 数与热电比交互作用下求得的目标函数的响应均值也没有变化，因此本文不再详述，其主要原因可能为:虽然满负荷运行最低延续h 数所在约束具有实际意义，但在热化系数求解过程中未能起到有效约束作用，最终导致了响应均值未发生变化。

通过热电比与其它重要因子的交互作用分析可知，热电比与其它因子的交互作用会对目标函数(系统煤炭供应成本)产生较为复杂的影响，但提高热电比往往会有助于降低煤炭供应成本。相关管理决策者通过合理调整热电比和因子的实际应用水平，可以在完成供热、发电任务前提下，降低煤炭消耗量，以期达到经济节能的目的。

图5 热电比与最低发电功率交互作用分析图Fig.5 Interaction plot of the lowest generated output and heat-power ratio

3 结论

本文基于无因次综合公式法，以中国北方某大型城市典型供热区域为案例，对采暖期供热负荷、供热量进行了预测，并以此为边界条件输入建立了以热化系数为决策变量的非线性优化模型，其后对模型中不确定参数因子对系统煤炭供应成本进行了交互作用分析。分析结果表明，热电比与其它因子的交互作用往往会对多热源供热系统煤炭供应成本产生重要影响，热电厂管理者可根据实际情况，在影响因子潜在波动区间内，制定适宜的机组运行方式(如依据实际情况提高热电比、改进技术降低供热、发电能耗和提高最低发电功率等)，在满足供热需求，发电上网－调峰的基础上，使得采暖期发电供热煤炭消耗总量降低，最终达到系统运行成本最优的目的。

［1］张沈生.城市供热模式评价理论方法及应用研究［D］.长春:吉林大学，1999.

［2］齐中英.工业热负荷最佳热化系数的计算［J］.热能动力工程，1991，6 (2):68－72.

［3］颜增祥.热电厂与区域锅炉房联合供热［D］.哈尔滨:哈尔滨工业大学，2009.

［4］武学素，张仲民，崔树庆，等.热化系数最佳值的确定方法［J］.西安交通大学学报，1988，22 (6):95－100.

［5］黄娇，赵静野.集中锅炉房调峰供暖系统的分析［J］.北京建筑工程学院学报，2008，24 (4):46－49.

［6］张晓萱，黄国和，席北斗，等.电厂优化配煤的不确定性机会约束非线性规划方法［J］.电机工程学报，2009，29 (5):11－15.

［7］方立军，武生，胡月龙，等.掺烧高炉煤气对锅炉传热特性影响的研究［J］.华北电力大学学报，2013，40 (1):66－70.

［8］Zhou Y，Huang G H，Yang B T.Water resources management under multi-parameter interactions:A factorial multi-stage stochastic programming approach［J］，Omega，2013，41 (3):559–573.

［9］Zhou Y，Huang G H.Factorial two-stage stochastic programming for water resources management［J］.Stochastic Environmental Research and Risk Assessment，2011，25 (1):67–78.

［10］贺平，孙刚，王飞，等.供热工程 (第四版)［M］.北京:中国建筑工业出版社，2009.

［11］城市热力网设计规范.CJJ 34－2010［S］.北京:中国标准出版社，2010.

［12］关健华，王冠，李岚，等.气候变化对沈阳冬季供暖期的影响［J］.气象与环境学报，2012，28 (6):72－75.

［13］李明宇，田卫东.修正热量法计算供热煤耗暨热电联产效益分析［J］.水利电力机械，2007，27 (5):55－58.