网孔电流法及其应用

袁 平 李忠相

(重庆市第一中学校 重庆 400030)

竞赛与物理专题研修

网孔电流法及其应用

袁 平 李忠相

(重庆市第一中学校 重庆 400030)

以网孔电流替代支路电流为求解对象的网孔电流法在求解复杂电路上具有明显优势，基于此介绍了网孔电流法的基本原理和在物理竞赛中的应用，并给出示例．

网孔电流法 基尔霍夫定律 复杂电路 等效电阻

1 用基尔霍夫定律解复杂电路

凡不能用电阻串并联等效变换化简的电路，一般称为复杂电路．在计算复杂电路的各种方法中，支路电流法是最基本的．它是应用基尔霍夫电流定律和电压定律分别对结点和回路列出所需要的方程组，而后解出各未知支路电流，即将各支路电流作为求解对象．

【例1】求解图1所示电路中各支路电流．其中电源电动势ε=1.4 V，内阻不计，R2=R3=R5=1 Ω．

图1 例1题图

解析：先在电路图上选定好未知支路电流的参考方向(图2)．电路中共4个结点，3个单孔回路，可列出4 - 1 = 3个结点电流方程组和3个回路电压方程组，即

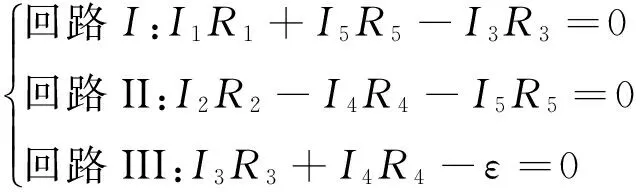
(1)

代入数据，即可解得

I0=1.0 AI1=0.4 A

I2=0.6 AI3=0.6 A

I4=0.4 AI5=-0.2 A

图2 选定参考方向

点评：利用基尔霍夫定律解题，虽然逻辑流程简洁，但是在实际手工运算中有两点极为不便．一是方程个数多，独立方程数目等于电路支路数，消元化简步骤多，计算极易出错；二是在列每个方程时，各项都要考虑正负号，费时且易出错．任何一个环节出错，都会导致满盘皆输，只得从头再来．

2 用网孔电流法解复杂电路

如果根据基尔霍夫定律，将上述求解过程稍做调整，用网孔电流替代支路电流作为求解对象，上述不便就将逐一化解．

所谓网孔电流，就是假想每个网孔对应一个独立的电流，同时属于两个网孔的支路，其电流等于两个网孔各自电流之和．例1所示电路有3个网孔，设如图3所示的3个网孔电流(为了区分实际电流，网孔电流可用i表示)．如果解出这3个网孔电流，各支路电流就都可以简单写出了．例如流过R1的电流I1=i1，流过R5的电流I5=i1-i2，其他支路情形类似．

图3 例1网孔法分析

显然，这样假设的网孔电流一定满足基尔霍夫电流定律，只需要根据基尔霍夫电压定律列出方程即可求解．每个网格设一个网孔电流，刚好每个网格可以列一个回路电压方程．对于第i个网孔回路，电压方程的通式为[1]

ii∑Ri-∑ipRip=∑εi

(2)

其中∑Ri为第i个网孔回路的总阻值，此项恒为正；-∑ipRip中ip是与第i个网孔相邻的第p个网孔对应的网孔电流，Rip是第i个网孔和第p个网孔共用的电阻，如果所有网孔电流均同为顺时针或同为逆时针，则此项恒为负；∑εi是第i个网孔回路的总电动势，与该网孔电流同向为正，反向为负．

对于例1所示电路，网孔电流法具体表达式为

(3)

代入数据，即可解得i1=0.4 A，i2=0.6 A，i3=1.0 A，再简单换算就可以得到各支路电流．

点评：通过实际运算会发现，网孔电流法完全解决了基尔霍夫的两点不便．一是方程数目明显减少，由等于电路支路数目变为等于网孔数目，大大简化了消元过程．二是每个方程具有固定的结构，除了电动势一项外其他各项均不需要判断正负号，大大降低了符号错误的可能性．电路越复杂，网孔电流法的优势就越明显．

3 用网孔电流法解电阻网络等效电阻

对于没有电源的纯电阻网络，也可以构造假想网孔电流，从而求解其等效电阻．

【例2】如图4所示“田”字形电阻网络，每小段电阻均为R，求A和B两点间的等效电阻．

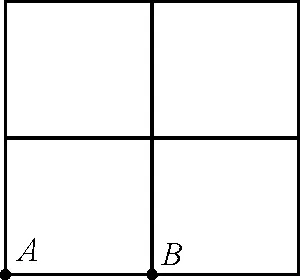
图4 例2题图

解析：假设有电流I从A点流入网络，从B点流出．电流在网络中的具体分布，采用网孔电流设出．提供外电流I的电路也设为一个网孔，但无需列出相应的方程，直接将I视为已知．如图5所示．对原网络的4个网孔列出电压方程,有

(4)

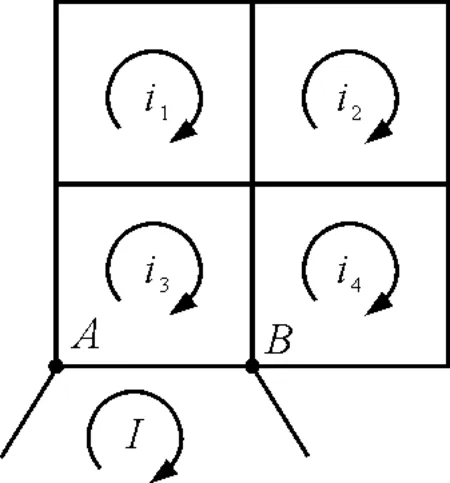
图5 例2网孔法分析

(5)

点评：求解电阻网络等效电阻的方法很多，比如等势点的断开与连接、星三变换、叠加法、电流分布法等．和这些方法相比较，网孔电流法对思维能力和运算能力要求均不太高，具有比较明显的优势．一旦掌握，一般会成为求解不对称电阻网络的首选方法．

4 用网孔电流法解多个重复电阻网络的电阻

【例3】如图6所示的电阻丝网络包含n≥3个正方形，网络中每一小段的电阻均为R，试求A和B之间的等效电阻RAB．

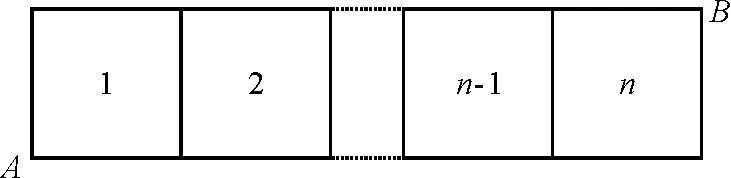
图6 例3题图

解析：此网络有n个单元，但各单元又有一定的相似性，无论用什么方法都不会太简单，我们尝试在网孔电流法的基础上寻求解决之道．假设有电流I从A点流入网络，从B点流出．电流在网络中的具体分布，采用网孔电流设出，如图7所示．

图7 例3网孔法分析

如果解出各网孔电流，由ACB路径，AB间的电压可以写为

UAB=2i1R+i2R+…in-1R+inR=

(i1+i2+…+in-1+in)R+i1R

(6)

由ADB路径，AB间的电压可以写为

UAB=(n+1)IR-

(i1R+i2R+…in-1R+2inR)=

(n+1)IR-(i1+i2+…+in-1+in)R-inR

(7)

将(6)、(7)两式相加即可消去各中间网孔的电流，有

(8)

由于对称性，AC段电流和DB段电流相等，即

i1=I-in

(9)

由(8)、(9)两式可得

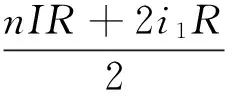
(10)

结合UAB=IRAB，可得

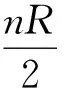
(11)

可见，只需要求出i1与I之比，即可得到AB间的等效电阻．

对各个网孔，列出回路电压方程，有

将各个网孔对应列出的回路电压方程化简为

(12)

可见，从第2个网孔到第n- 1个网孔，都具有相同结构的表达式

4ik-ik-1-ik+1-I=0

(13)

设上式可写为

ik+1-αik=β(ik-αik-1)-I

(14)

由式(13)、(14)对比可知

α+β=4αβ=1

(15)

解得

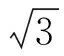
(16)

由式(14)累加，不难得到

in-1-αin-2=

βn-3(i2-αi1)-(1+β+…+βn-4)I

(17)

由对称性，有

i1=I-ini2=I-in-1i3=I-in-2

(18)

可解得

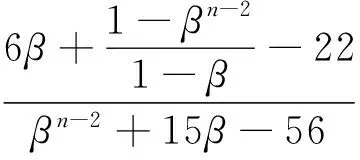
(19)

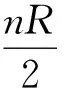
(20)

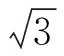
长期的教学实践表明，网孔电流法大大降低了解复杂电路计算出错的概率，在物理竞赛之类的考试中有非常重要的应用．从网孔电流法的原理不难理解，它不但适用于恒定电流电路，也适用于正弦交变电流电路[3]．但电路中如果有不满足叠加原理的非线性元件，叠加原理失效，此方法也就不能用了．

1 王凤池.网孔电流法.冀东学刊,1994(6):7～9

2 舒幼生,胡望雨,陈秉乾.物理学难题集萃(增订本).北京:高等教育出版社,1999.688～691

3 秦曾煌.电工学(第六版).北京:高等教育出版社,2004.129～130

2017-04-09)