类龙卷风涡动力学特征的数值研究

李春曦，郭 宁，李 娜，叶学民

(1.华北电力大学能源动力与机械工程学院，河北保定071003;2.陕西铁路工程职业技术学院，陕西渭南714000)

0 引言

龙卷风是一种剧烈旋转的地区性小尺度大气涡流，其突发性强、生消迅速，风速通常可达每s几十m 到一百m 以上，破坏力极大。目前，对龙卷风的研究主要通过理论、现场实测、实验室模拟及数值研究四方面进行［1～4］。龙卷风自身流场特性使得其现场实测极其困难，而实验室模拟［2］由于在涡旋表面和中心附近的强湍流移动，使得获取详细的流场特性也非常困难。近年来，数值模拟被广泛应用于龙卷风涡动力学的研究。Natarajan［3］应用LES 研究了平移和粗糙度对实验室尺度下类龙卷风的影响;Ishihara［4］模拟了两种典型的类龙卷风涡三维流场特性，并解释了流场形成的机制。

目前，对龙卷风的数值研究［3～5］大多基于实验室尺度的龙卷风发生装置，但以此长度比例引入粗糙度时，壁面粗糙度易落入气动力光滑区，从而与实际情况不符［5］。在以往研究中，因模型过于简单，或未考虑平移运动及表面粗糙度对风场的影响，因此不能较好地反映类龙卷风的实际流场结构。

为此，本文通过改进Ward 龙卷风模拟器，采用Fluent 软件对不同涡流比(0.2，0.42，0.64，1.0及2.0)下类龙卷风三维涡的流场特性进行数值模拟，从而分析龙卷风内部结构的动力特征。此外，为使类龙卷风模拟结果更接近实际，将风场附加平移运动并给定地表面粗糙度，进一步讨论其对流场结构的影响。

1 类龙卷风涡模型

所建龙卷风发生装置基于Ward 模型，包括汇流区、集聚区和对流区，如图1所示。汇流区的入口布置有导流板，用于改变进入集聚区的流体方向，从而产生不同旋转角动量;来自汇流区的空气流入集聚区中心，通过上升气流孔自旋向上进入对流区域。汇流区高度H0=112.68 m，其决定了空气进入集聚区的入流高度，上升气流孔的半径R0=112.68 m，该取值为全尺度龙卷风尺寸的最佳比例1/20［5］。由H0和R0确定的圆柱型区域是本文主要研究区域，其决定流场动力学特性。

图1 龙卷风发生装置模型Fig.1 Numerical model of tornado-like generator

对于类龙卷风涡，汇流区的高度、上升气流孔的半径及汇流区的入流角和速度是典型的流场控制变量，Lewellen［6］提出了控制流场的3 个无量纲参数，即涡流比S，径向雷诺数Rer，内部长宽比A。

式中:V0和U0分别为R0处的切向和径向速度，m/s;θ 为导流叶片角度;Q 为单位轴向长度的体积流量，m3/s。

涡流比S 是衡量相对于径向对流动量旋转能量的值，其决定类龙卷风涡的结构。涡流比和雷诺数控制流场的动力学特性，长宽比决定其几何结构。为衡量龙卷风涡旋，动力相似要求模型的涡流比和径向雷诺数与实际中全尺度的龙卷风相同。几何相似要求两者的流场边界成比例，即模型的长宽比和实际全尺度龙卷风相同。全尺度龙卷风的Rer一般取109～1011，雷诺数相对于涡流比来说重要性次之，在保证龙卷风气旋的内部动力特性相似时可不作考虑，只要Rer足够大使得流场为湍流即可［7］。因此，文中Rer为8 ×106～9 ×106可满足要求。

2 风场特性计算

2.1 Rankine 涡理论模型与数值模拟的比较

Rankine 涡为不考虑轴向流运动的二维涡，可反映龙卷风水平面流场的一般性规律。假定龙卷风在各平面上具有相同的平面流动:龙卷风涡核内形成强制涡，V =ωR。涡核外区，为自由涡旋有势流动，其旋转速度为V =Γ/2πR，其中Γ 是环流强度。这里用Rankine 涡模型与本文数值模拟出的龙卷风切向速度沿径向分布结果进行比较，以检验其正确性。

将Rankine 模型公式进行变形，并通过无量纲形式进行比较，可得

式中:v′为无量纲切向速度，v′ =V/VR(VR为最大切向速度);r′为无量纲半径，r′ =R/Rm(Rm为核心半径);χ 为修正参数，取0.9;c1和c2分别为调幅参数，取c1=0.95，c2=1。

选取S=0.42，高度Z=10 m 处切向速度沿径向的分布与上述公式进行比较，如图2所示。在核心半径内，切向速度近似呈线性增加，在核心半径处达到最大值;在核心半径外，切向速度呈指数减小。结果表明，二者吻合良好，即可用Rankine涡来近似描述龙卷风切向速度沿径向的分布，同时验证了模拟结果的准确性。

图2 Rankine 涡模型和数值模拟结果的比较Fig.2 Comparison of Rankine vortex model and numerical results

2.2 不同涡流比时的切向速度场

2.2.1 切向速度沿径向的分布特征

图3 为涡流比S =0.2，0.42，0.64 和1.0 时，高度在120 m 内切向速度沿径向的变化。为方便观察近地面的切向速度分布，在10 m 以下选取Z=2，5，8 m 三个截面。由图可知，随离中心距离的增加，切向速度迅速增加，在低涡流比时(图3a、3b)近似呈线性增长，在核心半径处切向速度达到最大，随半径增加逐渐减小，但其减小速率明显小于核心半径内速度的增长速率。在同一涡流比下，核心半径随高度逐渐增大，使龙卷风呈现漏斗型，这与和实际观测结果相符。随涡流比增加，核心半径和切向速度均增大，即相对于径向的对流动量，旋转能量增强。

对比图3 可知，S=0.2 时，地面附近Z =2 m，与其他高度相比，核心半径内切向速度有所减少;而高涡流比时，则切向速度明显增大，风压减小，风吸力增强。由于大多数建筑结构都位于这个区域，因此应该注重该区域结构的抗龙卷风设计。

2.2.2 切向速度沿高度的分布特征

图4 为不同涡流比下沿高度方向上的切向速度分布。对比图3 和图4 可知，在涡核外部，切向速度沿高度的分布类似于纵掠平板的常规湍流流动;涡核内部，在近地面处Z/R0=0.05 以内，切向速度变化剧烈，随高度增加波动逐渐减缓，如图4(b)～4(d)。因此，当龙卷风经过此区域时，大气压力场急剧变化，产生很强的吸力效应，将对地面上结构物造成严重破坏。

图3 不同涡流比时切向速度的径向分布Fig.3 Radial distribution of normalized tangential velocity for different swirl ratios

图4 不同涡流比时切向速度沿高度方向的分布Fig.4 Normalized tangential velocity distribution along the height direction for different swirl ratios

另外，对比图4(a)～4(d)发现，随涡流比增加，在Z/R0＞0.05 处，切向速度随高度变化波动逐渐增大。离核心半径越远，切向速度沿高度变化越趋于稳定，更接近于纵掠平板的常规流动。

2.3 不同涡流比时的静压力场

2.3.1 静压沿径向的分布特征

图5 为涡流比S =0.2，0.64 及2.0 时的类龙卷风静压沿径向的分布。由图可知，随半径增加，静压逐渐增大，在小涡流比时，涡核内的静压增长较快，近似呈线性变化;当S =0.64 和2.0 时，涡核中心附近静压几乎不变。在涡核外部，静压增长梯度相对核内有所减小，S=0.2 时，静压近似不变。此外，当S =0.2 时，可明显看出，随高度增加，核内静压逐渐减小;S=0.64 时，核内静压在不同高度处的变化差别极小，近似一致。

图5 不同涡流比时静压的径向分布Fig.5 Radial distribution of normalized pressure for different swirl ratios

2.3.2 静压沿高度的分布特征

图6 比较了类龙卷风风场静压沿高度方向的变化特征。在涡核内部，静压沿高度的分布呈曲线变化，和图5 核内静压分布相对应。地面附近静压迅速减小，其波动相对较大;然而在涡核外，静压沿高度方向几乎不变。对比图4 可知，高度对龙卷风静压的影响明显小于切向速度。

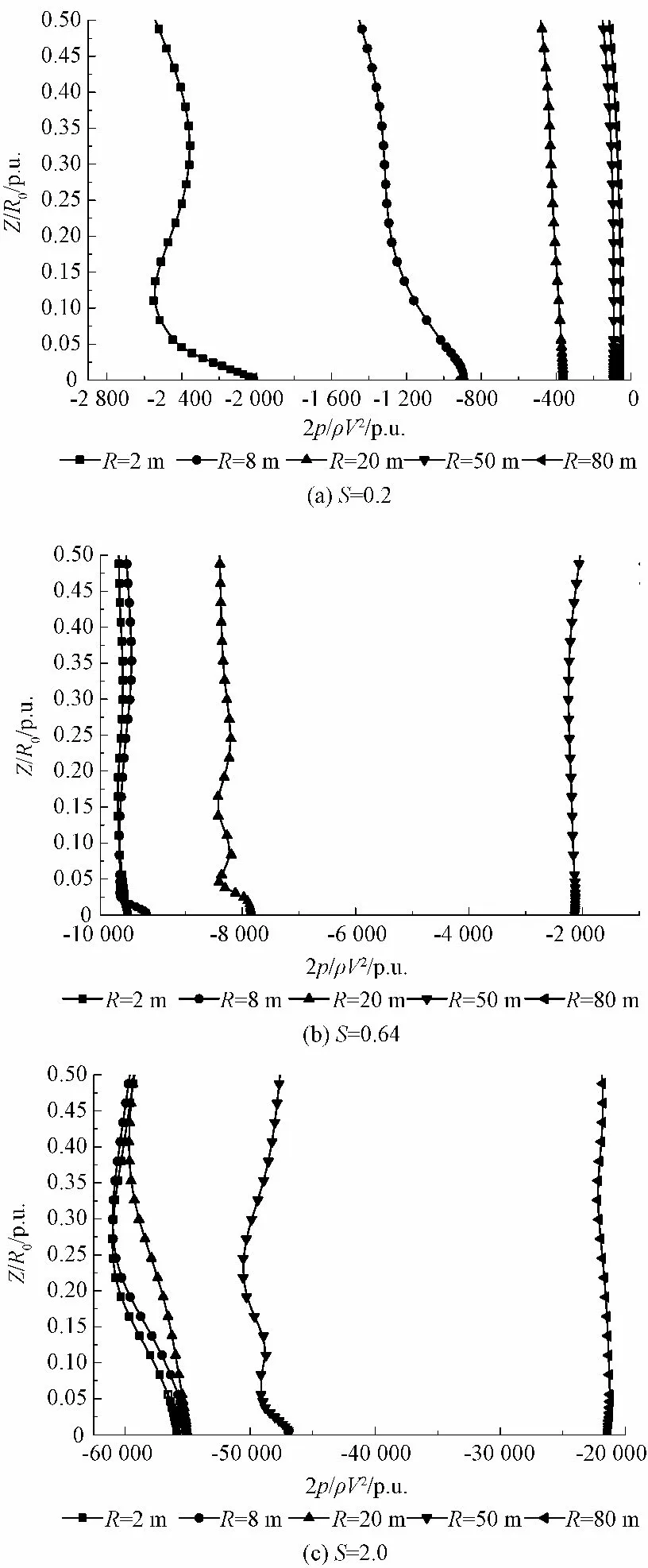
图6 不同涡流比时静压沿高度方向的分布Fig.6 Normalized pressure distribution along the height direction for different swirl ratios

3 平移对龙卷风风场的影响

考虑到实际中龙卷风除自身旋转外，还在垂直于地面的平面内做平移运动，因此数值模拟中，采用相对运动理论，保持涡旋静止，使地面相对于涡旋向相反的方向移动。模拟中给地面附加x 方向的平移速度，VT=1.193 m/s［8］。

图7 静止与附加平移后切向速度的径向分布Fig.7 Comparison of normalized tangential velocities for stationary and translating tornado－like vortices at height Z/R0 =0.01

3.1 附加平移后风场切向速度变化

图7 比较了不同涡流比时静止和附加平移速度后的切向速度分布。由图可知，附加平移后的涡旋中心明显向静止涡的右侧移动(图7 中涡平移由右向左)。当S=0.2，附加平移后，当R/R0＜0 时，相对于静止涡切向速度有明显降低，随涡流比增大，降低幅度逐渐减少，直至接近静止涡的速度分布。其原因是低涡流比时，平移影响占主要作用，使切向速度有所减小;随涡流比增加，平移产生的影响逐渐减小直至可忽略，此时切向速度接近静止涡的速度分布。

3.2 附加平移后风场静压变化

图8 为不同涡流比下静止和附加平移后的类龙卷风涡无量纲静压分布。低涡流比S =0.2 时，平移后的静压差系数相比静止涡旋显著减小，幅度为57 %。与切向速度相似，随涡流比增大，其减少幅度逐渐降低，最终和静止涡旋趋于一致。

图8 静止和附加平移后地面处静压的径向分布Fig.8 Comparison of normalized pressures for various swirl ratios of stationary and translating tornadolike vortices near the ground

综合图7 和图8 可知，低涡流比时，对类龙卷风涡旋附加平移运动使得近地面附近的切向速度和静压减少，这一影响产生的效果类似于低涡流比的静止涡旋特征。Fiedler 和Rotunno［9］研究表明，在低涡流比时，静止涡旋地面附近发现较大的速度是由于此处层流核心内超临界流的存在，基于该理论，平移后切向速度和静压的减少是由于平移导致层流被打破的缘故。

4 粗糙度对龙卷风风场的影响

表面粗糙度可通过物理建模粗糙元素，或通过等价的沙粒粗糙度来建模。在Fluent 中通过指定壁面边界条件的沙粒粗糙高度KS及粗糙度常数CS来引入表面粗糙度。为模拟地表面粗糙度对龙卷风风场的影响，须建立等价沙粒粗糙高度KS与空气动力学粗糙度长度y0之间的关系。基于大气边界层对数廓线拟合法和壁面函数的对数分布，Blocken 等［10］得到:KS=9.793y0/CS，在Fluent 中设置CS=0.5，因此可得KS≈20y0。本文中y0取0.1 m，即轻度粗糙程度，经代入及比例计算得KS=0.1 m。

图9 为光滑和粗糙地面在Z/R0=0.01 处最大切向速度与涡流比间的关系。该图表明，两种情况下变化趋势相似，粗糙度的引入使得地面附近处最大切向速度有所减小，这与文献中的实验及数值结果一致［11］，即地面粗糙度的增加造成该处附加的摩擦耗散，进而引起切向速度降低，对比可知，粗糙度的引入造成的影响类似于减小涡流比。

图9 光滑和粗糙地表面( Z/R0 =0.01) 处的最大切向速度随涡流比的变化Fig.9 The maximum tangential velocities along swirl ratios for smooth and rough ground surface at height Z/R0 =0.01

图10 比较了不同涡流比下光滑和粗糙两种地面上的龙卷风核心半径沿高度方向上的变化特征。由图可知，总体变化趋势一致，当Z/R0＜0.1时，计及粗糙度使得核心半径有所减小，这是由于表面粗糙度的增加导致近地面切向速度的减小，进而造成核心半径降低。然而，在Z/R0＞0.1 处，核心半径显著增大，这与文献［12］中结论相符。实验表明，随粗糙的增加，核心半径增加。综合对比图10 中4 组曲线可知，随涡流比增大，粗糙与光滑地面上，类龙卷风的核心半径之间的差值呈增大趋势。

图10 光滑和粗糙表面上核心半径沿高度的变化Fig.10 Distribution of core radius in height direction for tornado-like vortices on smooth and rough surface

5 结论

(1)随半径增加，龙卷风的切向速度沿径向先增后减。同一涡流比时，核心半径沿高度方向逐渐增加，呈漏斗型分布;随涡流比增大，切向速度和核心半径均提高;对于高涡流比，在近地面处，切向速度明显增大，其对抗风设计意义重大。对于切向速度沿高度方向的分布，在涡核外部，类似于纵掠平板的常规湍流流动;而涡核内部，在地面靠近核心半径处，随高度增加切向速度急剧增大。

(2)龙卷风风场静压沿径向分布呈上升趋势，但涡核内的增长速率明显大于涡核外。在涡核内部，静压沿高度的分布波动相对较大;而涡核外部，静压沿高度几乎不变。

(3)平移对龙卷风涡场的影响，随涡流比不同而变化。低涡流比时，切向速度和静压差均有所降低，但随涡流比增大，降低幅度逐渐减小，直至与静止涡旋的速度分布一致。粗糙度的引入降低了地面处最大切向速度，其结果相当于降低涡流比，核心半径也随之减小，但Z/R0＞0.1 时，核心半径却明显增加。

［1］刘式适，付遵涛，刘式达，等.龙卷风的漏斗结构理论［J］.地球物理学报，2004，47 (6):959－963.

［2］Ward N B.The exploration of certain features of tornado dynamics using a laboratory model［J］.Journal of Atmospheric Sciences，1972，29 (6):1194－1204.

［3］Natarajan D，Hangan H.Large eddy simulations of translation and surface roughness effects on tornado-like vortices［J］.Journal of Wind Engineering and Industrial Aerodynamics，2012，104:577－584.

［4］Ishihara T，Oh S，Tokuyama Y.Numerical study on flow fields of tornado-like vortices using the LES turbulence model［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99 (4):239－248.

［5］Natarajan D，Hangan H.Numerical study on the effects of surface roughness on tornado-like flows［C］.11th Americas Conference on Wind Engineering，San Juan，Puerto Rico，2009.

［6］Lewellen W S.A solution for three-dimensional vortex flows with strong circulation［J］.Journal of Fluid Mechanics 1962，14 (3):420－432.

［7］Church C R，Snow J T，Baker G L，et al.Characteristics of tornado-like vortices as a function of swirl ratio:a laboratory investigation［J］.Journal of the Atmospheric Sciences，1979，36 (9):1755－1776.

［8］Hangan H，Kim J D.Swirl ratio effects on tornado vortices in relation to the Fujita scale［J］.Wind and Structures，2008，11 (4):291－302.

［9］Fiedler B H，Rotunno R.A theory for the maximum wind speeds in tornado-like vortices［J］.Journal of the atmospheric sciences，1986，43 (21):2328－2340.

［10］Blocken B，Stathopoulos T，Carmeliet J.CFD simulation of the atmospheric boundary layer:wall function problems［J］.Atmospheric environment，2007，41(2):238－252.

［11］Rostek W F，Snow J T.Surface roughness effects on tornado like vortices［C］.The 14th Conference on Severe Local Storms of the American Meteorological Society，Indianapolis，Indiana，1985.

［12］Monji N，Wang Y.A laboratory investigation of the characteristics of tornado-like vortices over various rough surfaces［J］.Acta Meteorol Sin，1989，3:506－515.