规则波下张力腿平台时域响应分析

刘为民，谷家扬，卢燕祥

(江苏科技大学 船舶与海洋工程学院，江苏 镇江212003)

0 引 言

张力腿平台为半顺应半刚性复杂非线性系统。一方面，平台浮力远大于自重，因此，浮力一部分用于抵消自重，一部分用于张力腿预张力，使得张力腿始终处于紧绷状态，平面外运动较小，呈现刚性状态;另一方面，张力腿平台受外力作用，且水平方向分力较垂向分力大，水平方向运动幅度较大，又表现出柔性状态。平台利用张力腿与基础锚固相连，为平台上的生产、生活提供相对平稳安全的环境。

张力腿平台六自由度水动力特性分析如下:张力腿平台在水平面内具有柔性特点，其纵荡和横荡运动固有周期在100 ～200 s 内变动。张力腿平台的纵荡和横荡运动由周期性激励所致，关乎到整个平台的生产和生活安全，因此，纵荡和横荡成为评判张力腿平台水动力性能的重要指标之一。在进行张力腿平台设计时，需保证其纵荡和横荡运动位移不超过5%工作水深。张力腿平台的纵摇和横摇运动，会使各张力腿预张力发生变化，给整个平台提供回复力，在此期间，张力腿始终保持平行状态，并未松弛。张力腿平台纵摇和横摇固有周期通常小于4 s，固有频率大于波浪频率，摇摆角度为-3° ～3°。张力腿平台首摇运动固有周期通常大于40 s，张力腿如果不平行，则张力腿交点为横荡所引起的首摇旋转中心;张力腿如果始终保持平行，首摇激励必将减小，导致首摇运动减小。张力腿平台垂荡运动较小，其固有频率大于波浪频率，固有周期为2 ～4 s，垂荡运动易与纵荡运动相耦合。

王世圣等［1］(2011)利用SESAM 软件对南海环境条件下某一张力腿平台进行了运动响应分析，结果表明该平台能够满足1 500 m 水深南海环境条件的需要，且具有较好的运动性能。Y.M.low［2］(2010)采用等效线性化方法对张力腿平台回复力计算进行了整理，推导了大位移下回复力与刚度矩阵，对张力腿平台时域和频域结果进行了分析。王世圣等［3］(2007)利用Morison 公式和势流理论相结合的方法对4 种半潜式海洋平台运动性能进行了研究，分析了不同平台的频域及时域运动特点，对深水半潜式平台的选型具有一定指导作用。M.R.Tabeshpour 等［4］(2006)采用扰动法求得张力腿平台自由振动和强迫振动下的一阶和二阶近似解，对轴向载荷对平台运动的影响进行了研究。Xiaohong Chen 等［5］(2006)采用4 种不同方法(准静态法、软件WAMIT、基于辐射和绕射理论的COUPLE 软件及实验测量)对一微型张力腿平台进行了动力响应研究。结果表明准静态法只能在波浪频率范围内进行预报，而COUPLE 在各频率范围内的预报均较为精确。S.Chandrasekaran 等［6］(2007)采用斯托克斯波浪理论对五浪向(0°，30°，45°，60°和90°)下的某三角形张力腿平台进行了动力响应研究，计算过程中忽略了高频振动和低频纵荡运动。结果表明浪向角对各自由度(除垂荡)的影响较大，直线型运动呈现出一定的非线性。S.Chandrasekaran等［7］(2004)讨论了规则波下惯性力系数和拖曳力系数对2 座不同工作水深(600 m和1 200 m)张力腿平台运动响应的影响，采用Morison 公式和Newmark′s β 法对水动力和微分方程进行了求解。

1 力学模型

张力腿平台谐振运动方程如下:

式中:M 为频率相关矩阵;m 为张力腿平台质量矩阵;A 为频率相关附加质量;C 为频率相关势流矩阵;D1为线性阻尼矩阵;D2为二阶阻尼矩阵;f 为速度矢量函数;K 为水静力刚度矩阵;x 为位移矢量;q 为矢量激励力。激励力表示如下:

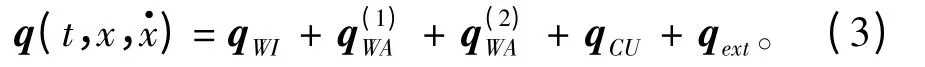
式中:qWI为风作用力;为一阶波浪激励力;为二阶波浪激励力;qCU为流作用力;qext为其他作用力，如波浪漂移力、特殊力等。

傅里叶逆变换:

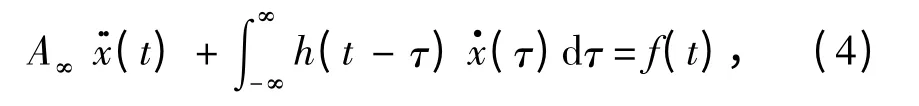
运动方程可变为:

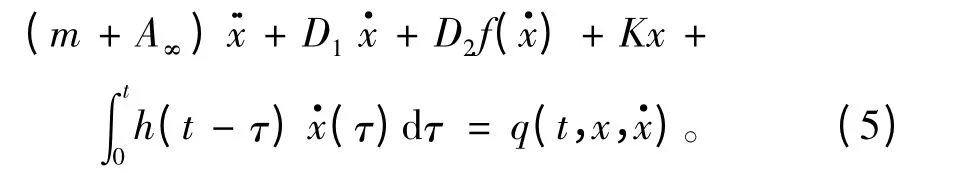
式中h(τ)可由频率相关附加质量和阻尼进行计算:

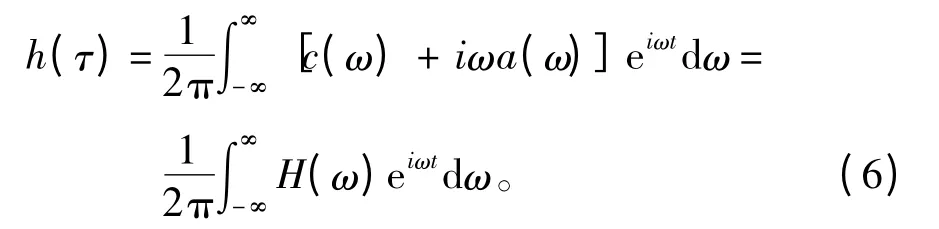
当τ ＜0 时，

h(τ)=0。

当τ ＞0 时，

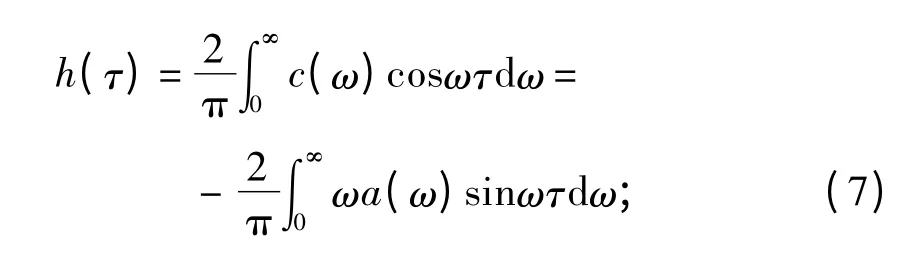
当τ=0 时，可得，

2 张力腿平台在规则波下的时域响应分析

本文的数值模型为:吃水26.6 m，张力腿根数12根，预张力1 048 t，张力筋腱轴向刚度35 000 000 N/m，工作水深为1 000 m。计算工况由不同波高(H=6 m，8 m，10 m)、不同波周期(T=10 s，12 s，14 s)及不同入射波角度(0°，15°，22.5°，30°，45°)组合而成，各工况标记为D* H* T*，如D0H6T10 表示入射波角度0°，波高6m，波周期10s 的计算工况。本文对不同入射波角度、波高和波周期展开讨论。

2.1 不同入射波角度对平台各水动力特性的影响

在相同波高和波周期下，不同入射波角度15°，22.5°，30°时张力腿平台六自由度水动力特性的计算结果如图1和图2所示(由于篇幅关系，部分图没有列出)。

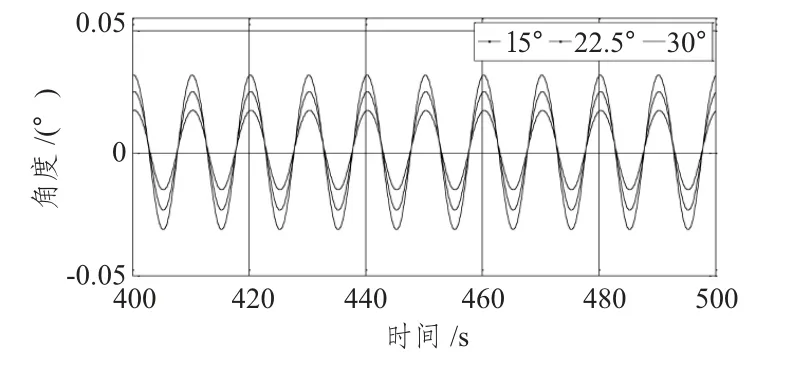
图1 不同入射波角度横摇时历曲线Fig.1 Time series of roll nder different directions

图2 不同入射波角度首摇时历曲线Fig.2 Time series of yaw under different directions

计算结果表明:入射波角对垂荡和纵摇的影响较小，尤其对纵摇的影响甚微，而入射波角对其他四自由度的影响较大;平面内运动较平面外运动大。随入射波角的增大，纵荡位移均值逐渐减小，纵荡平衡位置逐渐减小，纵荡位移波幅基本不变，横荡均值逐渐增大，表明横荡平衡位置逐渐增大。从图1 看出，横摇均值随入射波角的变化改变不大，其平衡位置也几乎不变;而横摇幅值随入射波角的增大而增大，增大约16%。从图2 分析可知，在15°和22.5°方向下，其最小值变化不大，均在0.52°左右，22.5°方向下最大值较15°大;30°方向下的均值较前两者小。综上所述，入射波角度对六自由度的影响不尽相同，这主要是由张力腿平台在不同方向上受力变化的不同及各自由度对入射波方向敏感性不同导致的。

2.2 不同波高对六自由度的影响

在0°入射波、相同波周期、不同波高下的计算结果如图3 ～图6所示(计算工况D0H6T10，D0H8T10和D0H10T10)。

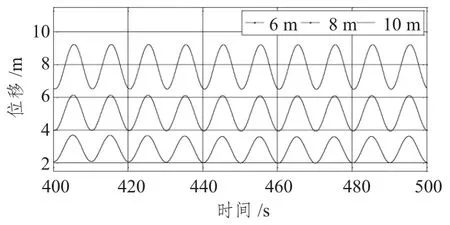
图3 不同入射波高度纵荡时历曲线Fig.3 Time series of surge under different wave heights

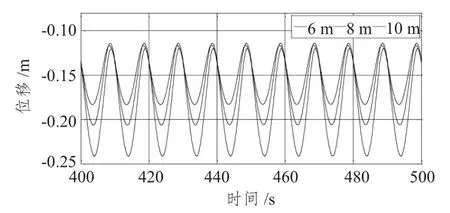
图4 不同入射波高度垂荡时历曲线Fig.4 Time series of heave under different wave heights

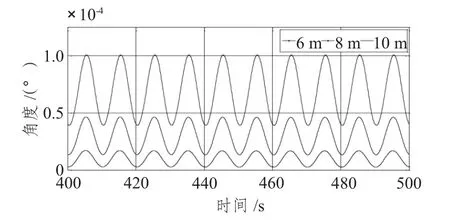
图5 不同入射波高度横摇时历曲线Fig.5 Time series of roll under different wave heights

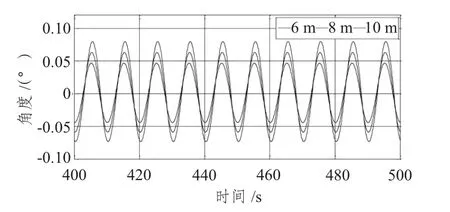
图6 不同入射波高度纵摇时历曲线Fig.6 Time series of pitch under different wave heights

从结果可知，除纵摇外，其他三自由度的均值均随波高的增大而增大。从图3 可知，随波高的增大，纵荡位移值的增长率逐渐增大，平衡位置值增大，幅值稍增大，平衡位置由2.8 变化为5，再变化为8(近似值)，增大约60%。从图4 分析可知，随波高的增大，垂荡最大幅值变化不大，最大位移值逐渐增大，垂荡平衡位置逐渐远离水平面，且有一定的相位差，这是由于不同波高产生不同垂向分力所造成的。如图5所示，随波高的增大，横摇值逐渐增大，幅值逐渐增大，平衡位置增长率逐渐增大。如图6所示，不同波高下，纵摇平衡位置几乎不变，但幅值随着波高增大而增大。综上所述，不同波高对纵荡及横摇的影响较大，对纵摇的影响次之，对垂荡的影响最小;这是由于不同自由度对波高的敏感性不同所导致的。

2.3 不同波周期对六自由度的影响

在0°入射波、相同波高、不同波周期下，计算结果如图7所示(工况D0H6T10，D0H6T12和D0H6T14)。

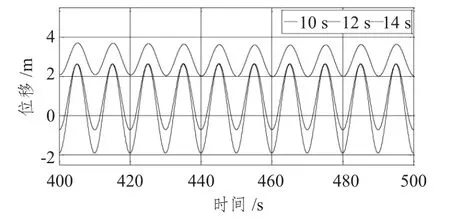
图7 不同入射波周期纵荡时历曲线Fig.7 Time series of surge under different wave periods

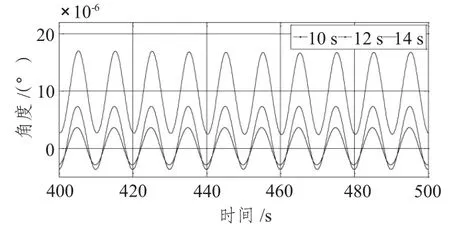
图8 不同入射波高度横摇时历曲线Fig.8 Time series of roll under different wave periods

结果显示，随波周期的增大，纵荡、垂荡、横摇和纵摇逐渐减小，其中纵荡与横摇的变化幅度更大。从图7 可知，10 s 周期下的纵荡均值比12 s 及14 s 下的纵荡均值大，12 s 周期下和14 s 周期下的纵荡最大值变化不大，但最小值不同;纵荡平衡位置随波周期的增大而减小。从图8 分析可知，周期10 s 下的横摇均值较12 s和14 s 下的横摇均值大，周期12 s和14 s 下的横摇最小值变化不大，但12 s 下的横摇最大值较14 s 下的横摇最大值大。不同波周期下，垂荡与纵摇的变化极为相似:时历曲线都存在相位差;平衡位置都基本不变;幅值也都变化不大。综上所述，由于波浪周期不同，平台所受力不同;各自由度对波周期的敏感性不同。

2.4 不同波浪参数对张力腿顶端预张力的影响

张力腿平台总布置及张力腿编号如图9所示。不同入射波方向、波高和波周期下T1(编号为1 的张力腿)顶端张力变化如图10 ～图12所示。结果显示，不同入射波方向对T1 的顶端张力影响很小，3 种入射波方向下的T1 顶端张力均值约为1.038×107，这种变化趋势与上述垂荡变化关系相似，也体现了垂荡与顶端张力的相互关系。分析图10 可知，随波高的增大，T1顶端张力幅值逐渐增大，且不同波高下T1 顶端张力变化存在一定的相位差。总的来说，不同入射波角度、波高和波周期对顶端张力的影响较小。本文中张力腿呈对称布置，因此只分析T1，T2，T3，T4，T5和T6。对比图11 与图12 可知，T1，T2，T3 的顶端张力均值及幅值均大于T4，T5，T6 的，这是由于T1，T2，T3位于T4，T5和T6 前侧，直接受力较大;且后侧的张力腿张力变化“滞后”于前侧的变化。

图9 张力腿平台总布置及张力腿编号Fig.9 Configuration of TLP with numbered tendons

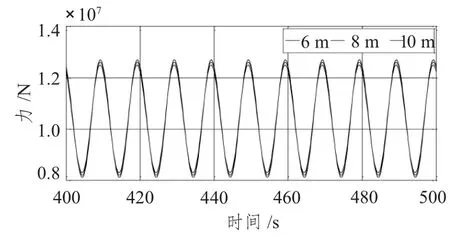
图10 不同波高下T1 顶端张力Fig.10 Top tension of T1 under different wave heights

图11 T1，T2，T3 顶端张力Fig.11 Top tension of T1，T2 and T3

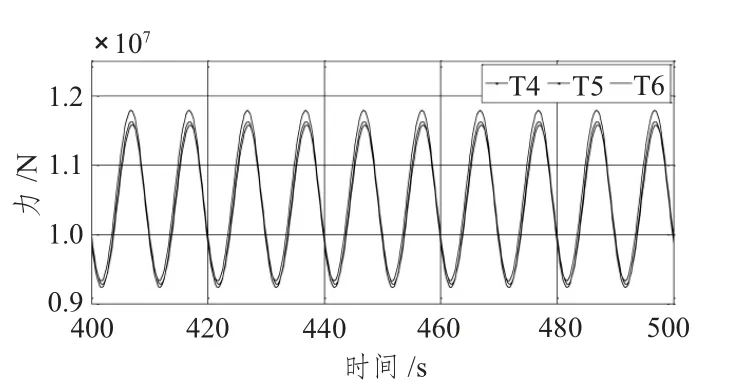
图12 T4，T5，T6 顶端张力Fig.12 Top tension of T4，T5 and T6

3 不同工作水深对张力腿平台运动的影响

由于张力腿平台在不同水深工作，因而张力腿长度会随水深变化，即使采用同一物理属性的张力腿，其轴向力仍有所不同，从而造成张力腿平台运动的不同。对500 m 水深和1 000 m 水深工作的张力腿平台进行模拟，其他参数相同，计算工况D0H6T10 下计算结果如图13 ～图14所示。

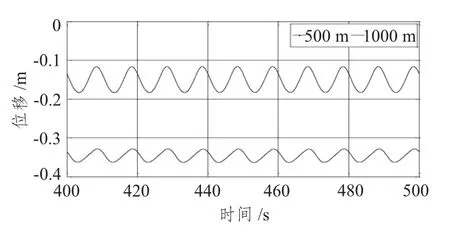
图13 不同工作水深垂荡时历曲线Fig.13 Time series of heave in different water depths

图14 不同工作水深横摇时历曲线Fig.14 Time series of roll in different water depths

对图14 进行分析可知，随着水深的增加，纵荡、垂荡和横摇的平衡位置逐渐增大，且幅值也均有所增大;而纵摇的平衡位置变化不大(两工作水深下，几乎为0)，但幅值随水深的增大而增大，1 000 m 工作水深下的纵摇幅值约为500 m 水深的2 倍，平衡位置几乎相同。从图13 分析，1 000 m 水深下的垂荡位移比500 m 下的小，这可能是由于垂荡与纵荡、横荡相耦合的结果。总体看来，1 000 m 工作水深下的张力腿较500 m 工作水深下所受振荡小，从而张力腿承受的载荷相对较小，更能保证张力腿的使用寿命。从图14 分析可知，不同工作水深下横摇的时历曲线存在相位差:当500 m 水深下横摇值达到最大时，1 000 m 水深下的达到最小值;1 000 m 水深下的平衡位置绝对值约为500 m 水深的2 倍。不同工作水深下的横荡和首摇时历曲线的变化均较小，因此不作赘述。综上，不同工作水深对张力腿平台的六自由度响应的影响颇大，这主要是由于张力腿轴向力变化所引起的。因此，在张力腿平台设计过程中，需结合平台所处位置、工作水深、张力腿材质、轴向刚度等参数，选取合适的张力腿。

4 不同吃水对张力腿平台运动的影响

由于张力腿平台吃水不同，必然导致张力腿平台浮力发生改变，各张力腿顶端张力发生变化。对吃水分别为21.6 m，26.6 m和31.6 m 的模型进行模拟，计算工况D0H6T10 下的计算结果如图15 ～图16所示。

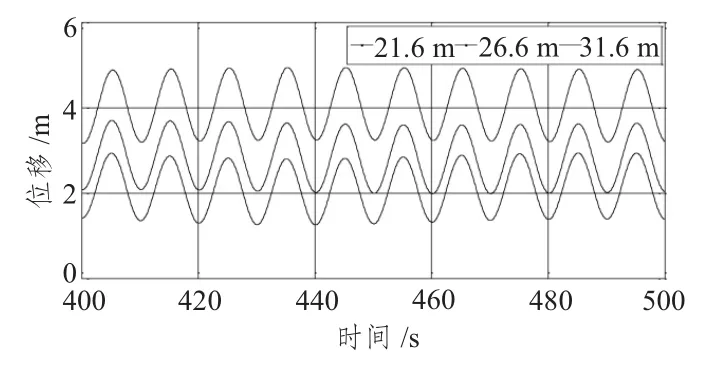
图15 不同吃水下纵荡时历曲线Fig.15 Time series of surge under different drafts

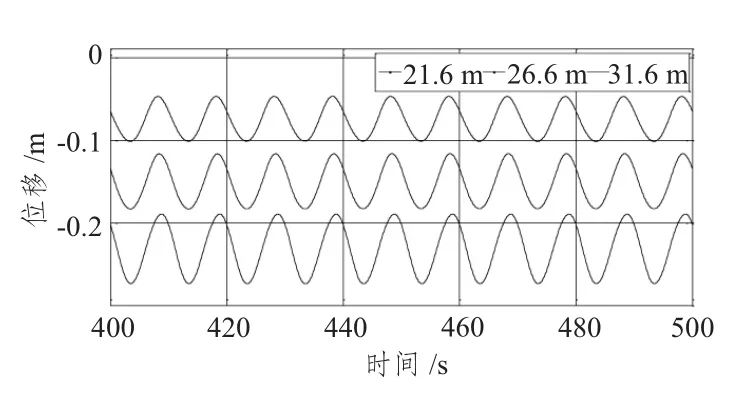
图16 不同吃水下垂荡时历曲线Fig.16 Time series of heave under different drafts

从计算结果分析可知，随着吃水的增大，各自由度下位移幅值逐渐减小，这是由于浮力减小后，张力腿平台更容易发生漂移的缘故而造成的;纵摇值对不同吃水的敏感性较小，时历曲线几乎变化不大。从图15 分析可知，随着吃水的减小，纵荡位移值的增长率逐渐增大，平衡位置值增大分别为30%和50%左右;纵荡位移幅值的变化不明显。从图16分析可知，随吃水的减小，垂荡幅值的变化不明显，但其平衡位置值成倍增大。不同吃水下横荡和首摇时历曲线变化很小。综上所述，不同吃水对纵荡和垂荡的幅值影响不大，但对平衡位置影响很大;同样的，不同吃水对横摇的幅值及平衡位置影响明显，而不同吃水对纵摇影响甚微。

5 不同张力腿数目对张力腿平台运动的影响

张力腿数目的不同对张力腿平台的受力分布具有直接影响，从而导致张力腿平台运动情况的不同，12 根张力腿布置如图9所示，8 根张力腿布置如图17所示。不同张力腿数目在计算工况D0H6T10 下对纵摇、纵荡和垂荡的模拟计算结果如图17 ～图18所示。

图17 8 根张力腿布置图Fig.17 Configuration of TLP with eight tendons

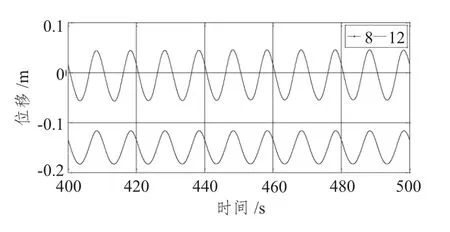
图18 不同张力腿数目垂荡时历曲线Fig.18 Time series of heave with different tendons

从计算结果分析可知，总体来说，不同张力腿数目对纵摇和纵荡的影响不是太大:张力腿数目为8 时，其纵摇幅值较12 根的要大，但平衡位置几乎不变。当波作用于张力腿平台时:前期，8 张力腿的平台纵荡位移不稳定，待一定时段后，又趋于稳定状态，如此反复。这充分说明8 根张力腿的平台与12 根张力腿的平台相比，前者极其不稳定，不利于作业及人员安全。从图16和图18 比较分析可知，8 根张力腿下垂荡平衡位置在0 m 左右，而12 根张力腿下的却比8 根下的远0.15 m 左右;8 根张力腿下的垂荡幅值较12 根张力腿的大。

6 结 语

本文主要对张力腿平台动力响应力学模型进行分析，研究了规则波下张力腿平台时域响应运动特性。对比分析了入射波角度(15°，22.5°和45°)，波高(6 m，8 m和10 m)及波周期(10 s，12 s和14 s)对张力腿平台各自由度运动、顶端张力的影响;探讨了吃水高度、工作水深、不同张力腿数目对张力腿平台运动特性的影响。主要结论如下:

1)由于张力腿平台各自由度对入射波角度、波高和波周期敏感度不同，使得张力腿平台在不同波浪参数下的运动特性(如位移幅值、平衡位置等)及顶端张力表现各异;

2)不同吃水下的张力腿平台位移大小、平衡位置和运动方向等均不同。工作水深越大，各自由度运动越剧烈，体现了工作环境对张力腿平台运动具有较大影响。

3)张力腿平台各立柱角上张力腿数目越多，张力腿平台运动的位移、幅度等越小，随时间变化也越稳定。

［1］王世圣，谢彬，李新仲.在南海环境条件下深水典型TLP的运动响应分析［J］.中国造船，2011，52(1):94-101.

［2］LOW Y M.Frequency domain analysis of a tension leg platform with statistical linearization of the tendon restoring forces［J］.Marine Structures，2009:1-24.

［3］王世圣，谢彬，曾恒一.3000 米深水半潜式钻井平台运动性能［J］.中国海上油气，2007(4):277-280.

［4］TABLEESHPOUR M R，GOLAFSHANI A A，SEIF M S.Second-order perturbation added mass fluctuation on vertical vibration of tension leg platforms［J］.Marine Structures，2006(19):271-283.

［5］CHEN Xiao-hong，DING Yu，ZHANG Jun，et al.Coupled dynamic analysis of a mini TLP:comparison with measurements［J］.Ocean Engineering，2006，33:93-117.

［6］CHANDRASEKARAN S，JAIN A K，GUPTA A.Influence of wave approach angle on TLP′s response［J］.Ocean Engineering，2007，34:1322-1327.

［7］CHANDRASEKARAN S，JAIN A K，CHANDAK N R.Influence of hydrodynamic coefficients in the response behavior of triangular TLPs in regular waves［J］.Ocean Engineering，2004，31:2319-2342.