基于Ansys子模型法的肘板结构优化
2014-12-05史战新
史战新
(武汉第二船舶设计研究所,湖北 武汉430064)
0 引 言
肘板结构是容器结构节点的重要连接形式,外压容器平面舱壁与耐压壳体连接处的肘板趾端由于变形不协调,应力集中严重,容易产生疲劳裂纹。提高疲劳强度的根本方法是降低热点处的拉应力,而结构形式是降低应力集中提高疲劳寿命的主导因素。本文基于Ansys 子模型分析法对弧形肘板进行参数化建模,获得弹塑性应力应变历程,利用局部应力应变疲劳估算法进行弧形肘板疲劳特性分析,最后采用Matlab 与Ansys 联合仿真进行遗传算法优化设计。优化后弧形肘板较初始假定模型重量减轻,疲劳寿命大大提高。
1 Ansys 子模型法
1.1 子模型原理
子模型法基于圣维南原理,即如果实际分布载荷被等效载荷代替后,应力和应变只在载荷施加的位置附近有改变。因此只要子模型切割边界避开载荷集中及应力集中位置,子模型内部就可以得到较精确的解[1]。Ansys 子模型法先建立局部模型,再切割边界位移插值,将粗的整体模型的求解结果如位移作为局部子模型的边界条件进行细化网格求解。
1.2 模型优点[2]如下:
1)减少甚至取消有限元实体模型中所需的复杂传递区域;
2)方便用户在感兴趣的关键区域就不同的设计进行快速优化;
3)通过粗细网格对比帮助用户验证网格划分是否够细。
1.3 采用子模型的限制
1)全模型切割边界插值只能经过实体或壳单元,子模型中可以有其他单元如梁单元作为加强筋或由壳体单元变为实体单元;
2)子模型边界必须远离应力集中区域,在子模型计算后应就边界处的应力水平与整体全模型进行比对。
1.4 采用子模型法的步骤
1)生成并分析较粗糙的整体模型,保留模型db 文件及结果rst 文件;
2)生成子模型并划分好网格,生成节点;
3)提取保存子模型边界节点为后缀为.node 文件,默认文件名与子模型一致,命令为“nwrite’;
4)在子模型工作环境下恢复整体模型db 文件,在后处理模块读入整体模型结果文件,利用命令“cbdof”形成子模型边界插值文件,后缀为.cbdo;
5)恢复子模型db 文件,在求解模块读入上一步生成的cbdo 文件,并根据子模型范围内实际位移边界条件及外载荷加载求解;
6)验证子模型切割边界应力分布与整体全模型切割边界应力分布是否基本一致。
2 假定整体模型
2.1 结构模型
为了真实模拟耐压平面舱壁的受力状态,根据圣维南原理,当离开不连续体的距离大于时(R 为耐压壳体内径,δ 为壳体厚度),边缘及应力集中处的附加应力的影响可以忽略不计。因此建立内径为9 200 mm,长度为8 300 mm 的假定耐压圆柱壳体模型,耐压平面舱壁距离左右边界分别为2 900 mm和5 400 mm。
由于本文研究肘板结构的局部应力应变响应,故在建立几何模型时考虑肋骨、各类肘板等详细的边角特征,并进行有限元模型板厚偏置。
2.2 边界条件
在计算压力下,加筋板壳将会产生大变形,局部结构不连续处会产生大的应力集中,导致构件局部进入塑性状态,计算压力下肘板结构力学模型已不适用线弹性克希霍夫-勒夫薄板理论,从而应该应用弹塑性力学进行有限元求解。考虑到减少横舱壁构架承受沿构架长度方向的压力,形成复杂弯曲梁,同时为减小耐压壳板与横舱壁构架的应力集中程度,横舱壁构架布置于耐压舱室外。耐压舱室壳板及舱壁板施加计算压力4.9 MPa。耐压壳体耐压端口边界施加全约束,采用mm,N,MPa,t 单位制,如图2所示。
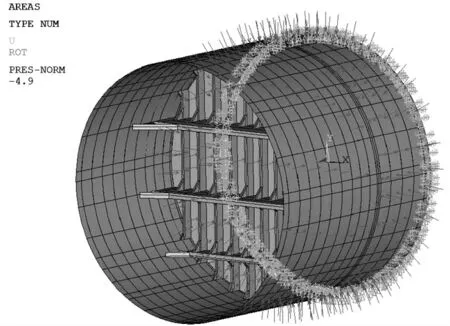
图2 有限元模型Fig.2 The FEM model
2.3 模型单元选择及计算设置
Shell281 是8 节点2 阶可导形函数单元,具有弹塑性、大变形、大应变等非线性分析功能。
本文计算中打开大变形开关,采用稀疏矩阵求解器及完全NR(NROPT,FULL,ON)迭代,使用渐进式加载(KBC=0),打开自动时间步长及线性搜索,最小子步为10,最大子步为100。收敛准则采用L2 范数即通过检查所有自由度方向上的不平衡力(或力矩)的平方和的平方根指标进行收敛检查,对于工程计算一般误差小于5%就可以接受。本文设置力的L2 范数收敛准则为1%(默认为0.001),以加快收敛。
2.4 整体模型粗网格计算结果
采用100 mm 四边形网格划分进行全模型进行大变形材料非线性分析,结果如图3所示。
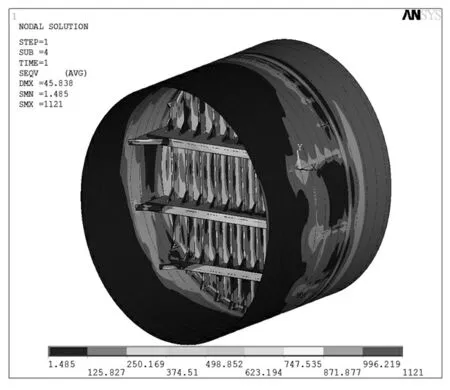
图3 粗网格整体模型结果Fig.3 The coarse grid model results
3 子模型分析
3.1 三角形肘板子模型
由于子模型的切割边界要远离应立集中区域,边界的选取也要经过尝试验证后才能确定,根据整体模型应力分布初步选取Z 方向范围(1 300 ~8 300)、X 方向范围(1 325 ~4 600)、Y 方向范围(350 ~3 100),其在全局坐标系下的位置与全模型中一致,如图4所示。
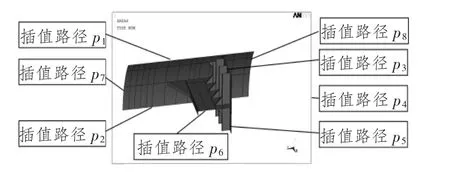
图4 子模型几何模型Fig.4 Sub-model geometry
3.2 三角形肘板子模型网格划分
采用25 mm 方形映射网格划分,如图5所示。

图5 子模型10 mm 映射网格Fig.5 10 mm mapped meshing of sub-model
3.3 三角形肘板子模型边界位移插值
子模型加载插值边界及部分壳板、横舱壁水压力载荷边界条件后,如图6所示。
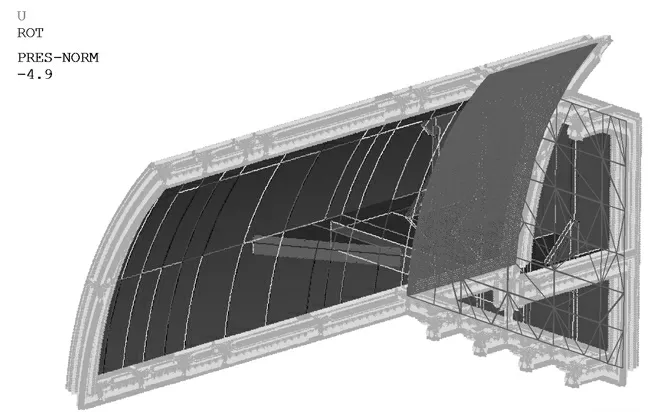
图6 子模型边界插值及加载Fig.6 Boundary interpolation and loading of sub-model
3.4 三角形肘板子模型边界位移插值
求解后应力分布如图7所示。
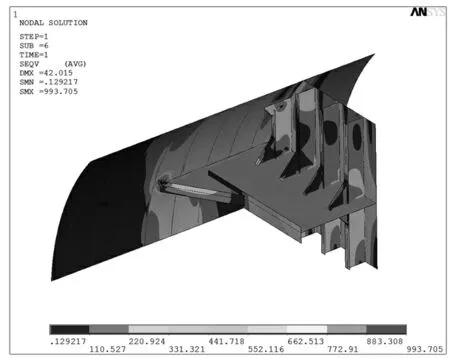
图7 子模型未平均表面mises 应力Fig.7 Not average surface mises and first principal stress distribution of sub-model
验证边界插值的准确性,进行路径插值分析比对,如图8 ~图9所示。根据对比,在边界上子模型与全模型的应力分布与大小基本一致,可以认为子模型边界选取基本合适。
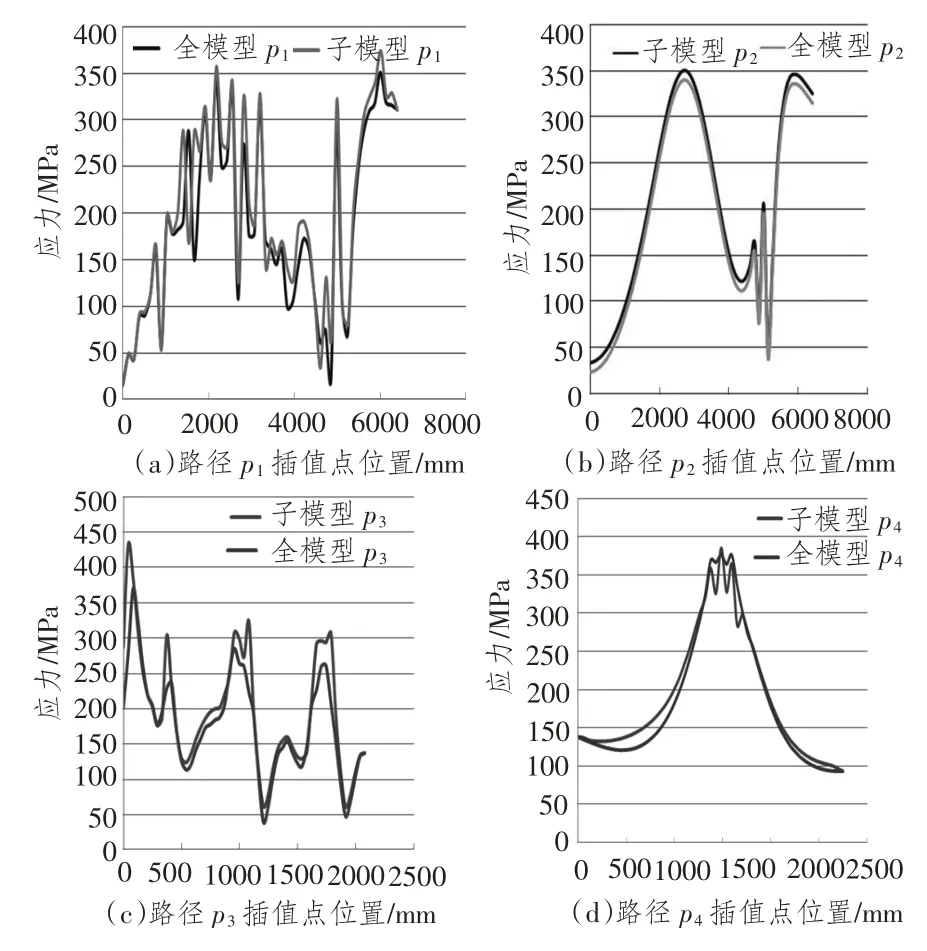
图8 切割边界路径1 ~3 应力比较Fig.8 Stress comparison of cutting edge path 1 ~3
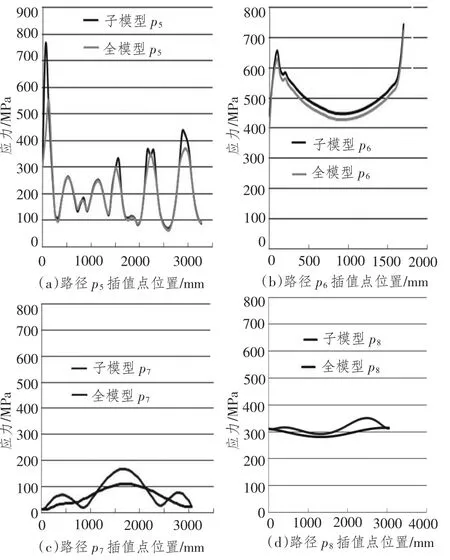
图9 切割边界路径4 ~8 应力比较Fig.9 Stress comparison of cutting edge path 4 ~8
尽管采用高阶壳单元弹塑性分析一定程度上可以避免几何奇异造成的应力集中,但应力集中无法消除。应力集中主要在3 个位置:①肘板端部焊趾及焊趾周围壳板,应力集中最为严重;②各肋骨与横梁相交处;③横梁角隅。如图10所示。
3 处应力集中是一个整体,相互影响,相互作用。其中位置1 主要由肘板与壳板刚度决定,位置2 主要由横梁整体(含肘板)与壳板肋骨的刚度协调性决定,位置3 主要由横梁角隅设计形式决定。一般解决位置3 处应力集中可以在横梁角隅根部开应力释放孔,圆孔半径一般不超过横梁高度的1/4。而通过改善肘板结构的形状降低刚度剧烈差异来形成各结构位移协调,是改善位置1和位置2 处应力集中的关键。
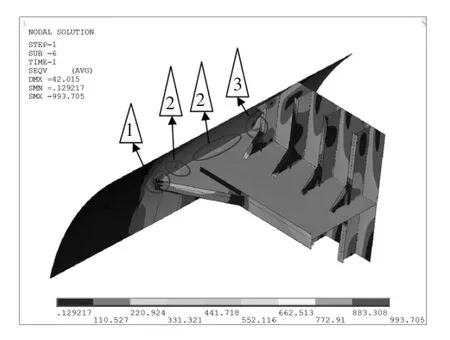
图10 应力集中位置未平均表面应力分布Fig.10 Not average surface stress distribution of stress concentration position
3.5 弧形肘板子模型
鉴于弧形肘板已成为各船级社共同推荐的结构形式,但在具体细节如外载环境、焊趾高度、弧度大小与横梁关系等方面有差别。经上文计算可知子模型边界划分合理,肘板应力集中位置远离子模型边界,改变肘板局部形状不影响子模型边界的位移应力分布,故采用如下改进方案:
采用肘板宽高等长构造弧形腹板,面板依腹板变化为矩形曲面,此类型肘板制造方便,肘板刚度较三角形肘板降低,横梁端部变形与壳板协调性增加。计算结果表明肘板刚度的减小带来了位置1 处由原来的应力993.75 MPa 降为918.37 MPa,降低7.5%,同时各肋骨线处应力集中明显下降,如图11所示。
从弧形肘板弹塑性分析来看,Full 模式显示下,弧形肘板的最大应力点与最大应变点位置不同,最大应变点的应力较小,最大应力点的应变较小,同时它们的应力应变载荷历程响应存在着差异,最大应变位置是未平均表面应力最大的位置,其应力在0.7 s 子步达到屈服极限,并开始塑性变形,而最大应力位置点则在0.95 s 子步进入塑性状态,应力比前者稍大,如图12 ~图15所示。应力集中区域在进入塑性后,局部位置产生大应变,总体结构刚度矩阵随载荷非线性变化。尽管不同位置点应力大小接近,但其应变历程不同,而且在Power Graphics模式下,最大应变点与最大应力点重合,也表明弧形肘板结构应力集中位置先进入塑性,大应变产生后,结构应力分布根据新的刚度矩阵发生变化,应变最大点塑性区域扩展至内部及其他附近区域。
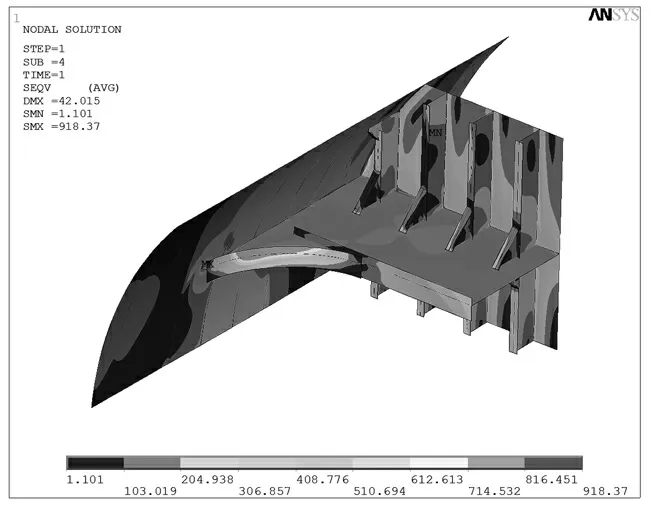
图11 4.9 MPa 弧形腹板未平均表面应力分布图Fig.11 Not average surface stress distribution of curved bracket at 4.9 MPa

图12 最大应力点应力应变历程曲线Fig.12 Stress-strain process curve of biggest stress points
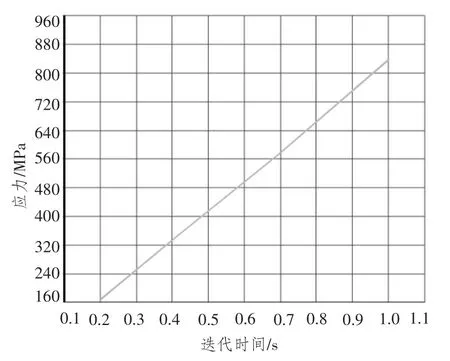
图13 最大应力点应力随时间变化曲线Fig.13 Stress-time process curve of biggest stress points
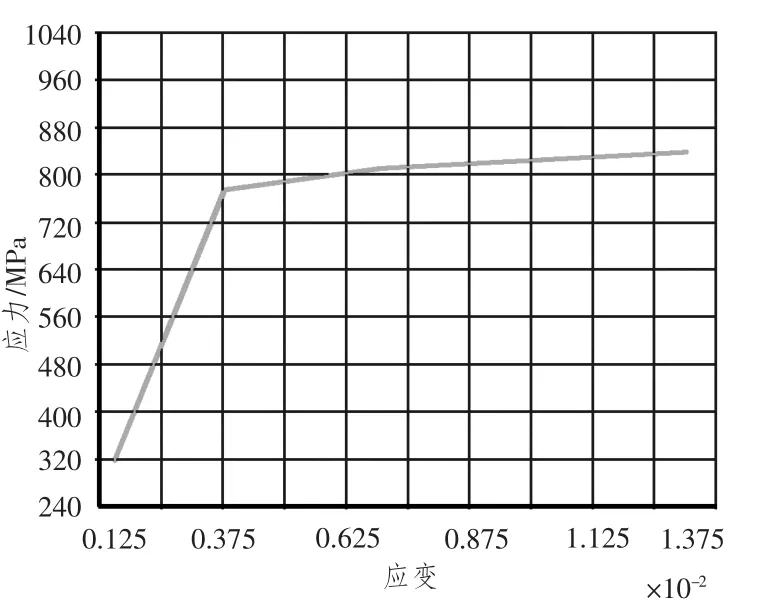
图14 最大应变点应力应变历程曲线Fig.14 Stress-strain process curve of biggest strain points
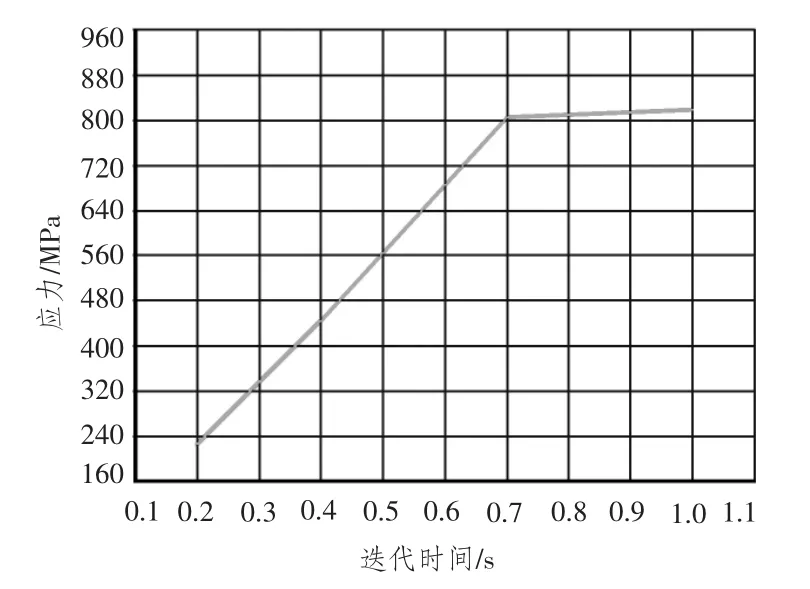
图15 最大应变点应力随迭代时间变化曲线Fig.15 Stress-time process curve of biggest strain points
4 肘板结构疲劳分析
FE-SAFE 软件疲劳分析中双轴应变疲劳基于局部应力应变方法,主要用于低周疲劳寿命估算,其中Brown Miller 算法适合绝大多数金属材料,对于韧性金属给出比较精确的结果,对脆性金属产生非保守值,使用弹塑性应力时,可提供多轴弹塑性修正。
Brown Miller 公式如下[3]:
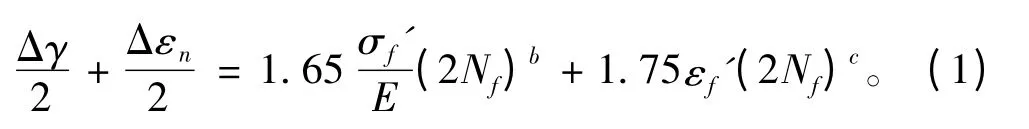
平均应力修正采用适合低周疲劳修正的Morrow 法:
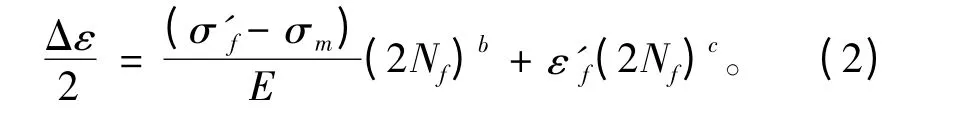
根据假定材料疲劳特性参数,利用曼森-柯芬应变疲劳寿命公式等,就可以获得稳态应力-应变循环曲线、应变疲劳寿命曲线,同时考虑工程上钢板表面一般粗糙度Ra=12.5,故软件表面系数设为4 ~16μm 等级,材料缺陷、加载频率、海水介质等影响因素已在经过试验得出的材料应变疲劳曲线中予以考虑。
将4.9 MPa 下的结构弹塑性应力应变数据输入Fesafe 软件,采用Morrow 平均应力修正方法,考虑残余应力[4]0.68σs=558 MPa,进行0 ~500 m 弹塑性循环加载如图16所示,局部应力应变法获得三角形肘板疲劳结果如图17所示,图中显示疲劳寿命最小点肘板端部应力集中处,为101.948=88 次。
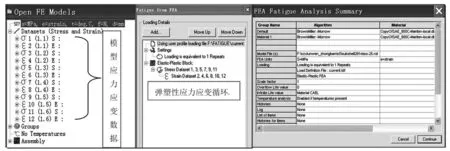
图16 三角形肘板弹塑性疲劳寿命分析设置Fig.16 Elastic-plastic fatigue life analysis settings of triangle bracket
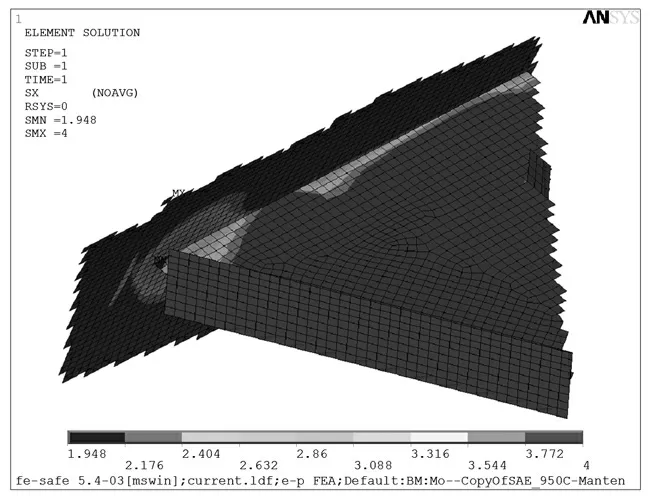
图17 三角形肘板弹塑性疲劳寿命分析Fig.17 Elastic-plastic fatigue life analysis of triangle bracket
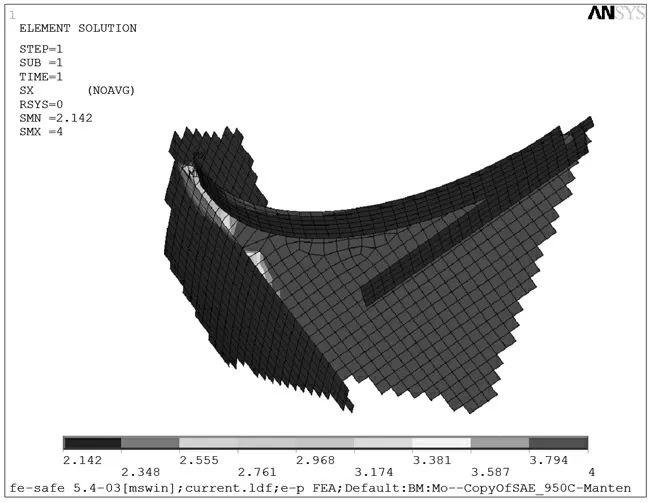
图18 弧形肘板弹塑性疲劳寿命分析Fig.18 Elastic-plastic fatigue life analysis of curved bracket
同理计算3.5 节弧形肘板弹塑性应力应变响应,局部应力应变法获得弧形肘板疲劳结果如图18所示。图18 显示,疲劳寿命最小点位于肘板端部应力集中处,最小循环此数在肘板端部为102.142=138次,比三角形肘板寿命提高了56.8%。
5 肘板结构优化
5.1 肘板参数化子模型
本文就弧形肘板利用Ansys 自动导圆功能在肘板腹板垂直边之间构造弧线过渡,由于肘板两边V(I,5),V(I,6)垂直,故随着V(I,1),V(I,2),V(I,5),V(I,6),V(I,7)和V(I,8)变化,弧形是圆的一部分或者椭圆的一部分。其中肘板尺寸参数数组变量设置如图19所示。
1)变量设置
变量范围为:v(I,1)∈[400 1500];v(I,2)∈[400 1800];v(I,3)∈[50 80];v(I,4)∈[50 80];v(I,5)∈[5 100];v(I,6)∈[5 300];v(I,7)∈[10 30];v(I,8)∈[10 30];v(I,9)∈[60 80];v(I,10)∈[80 90];v(I,11)∈[100 180]。
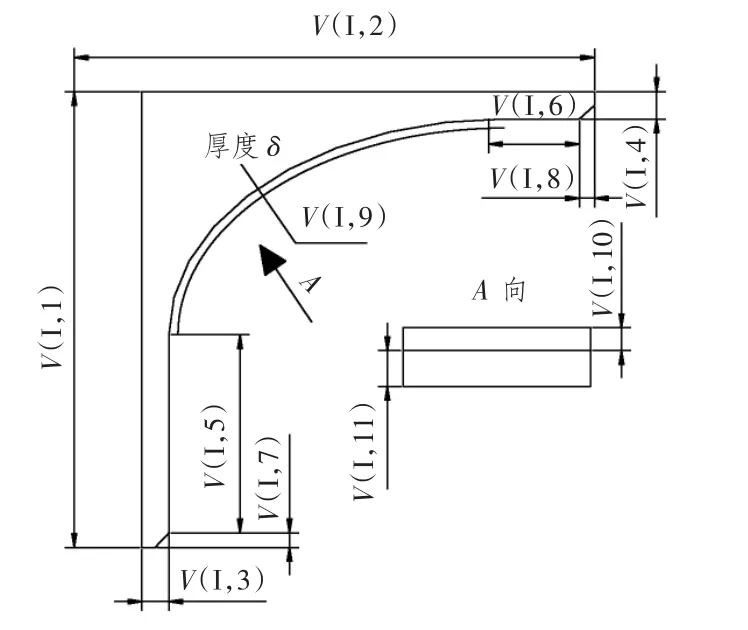
图19 子模型中局部肘板参数设置Fig.19 Local bracket parameter settings of sub-model
2)Ansys 子模型几何参数筛选优化
为加快收敛及实现对种群个体的一个迭代子步内循环求解,需要对几何参数变量进行筛选优化和迭代计算。若在Matlab 中对参数变量进行筛选,则会造成种群数组的不匹配,不利于进行交叉变异。因此在Ansys 中采用循环结构对Matlab 输出参数进行求解,不合理参数的目标值直接赋予大数以便在Matlab 中排除,符合的继续进行求解。
3)子模型目标参数输出选择
提高压力容器疲劳强度的根本方法是降低热点处的拉应力,即Anysys 应力结果的第一主应力S1,而S1 与Mises 应力正相关,且弹塑性材料的屈服判断准则为Mises 准则,故本文采用Mises 应力反应疲劳寿命的高低。本文采用子模型质量和子模型最大平均应力点应力进行双目标优化。
5.2 Matlab 优化控制程序
基于Sheffield 大学Gatbs 遗传算法工具箱进行编程设计如下:
1)设计变量
将子模型中肘板的11 个尺寸参数作为设计变量,在Matlab 中设置变量范围区间,初始二进制随机种群,初始十进制随机变量种群。
2)约束条件
为了保证优化后模型处于弹性应变状态,假定材料屈服极限σs为820 MPa,对应应变为0.004,由于模型进入弹塑性后应力与应变不再是线性关系,因此子模型优化时约束最大应变小于0.004 较为合理,另外约束最大剪应力应小于0.57σs=467 MPa。
3)目标函数建立
将Ansys 输出的肘板体积乘以密度转换重量值作为目标函数1,将Ansys 中输出的最大应力值作为目标函数2。根据约束条件加入惩罚因子对目标函数1 进行筛选,加速优化速度。
4)交叉率和变异率函数建立
根据遗传算法的特点在迭代后期,种群个体趋向最优解,为了保持优良个体的稳定,应根据迭代次数采用较小的交叉率和变异率。log(pmmin/pmmax)为最大与最小变异率比值的对数解,保证在最后一次迭代变异率为pmin。
5)种群处理技巧
对于双目标优化,种群个体要分为两部分,分别输入2 个目标函数,并根据适应度函数进行排序按照预定代沟进行优选。当种群个体为奇数时,分流会出现例如chrom(1:4.5)的情况,A 中个体数目其实等效于chrom(1:4)中数组数目,而在进行目标函数优选时,select 函数将变量个体数目乘以代沟后,采取四舍五入的取值规则,这样就造成了目标值与变量值的数量不统一。为了实现无论种群个体奇数、偶数都能顺利实现分流、优选、重组、交叉变异,采取种群个体数量先行取整分组。
6)遗传迭代处理技巧
为了加快迭代效率,减少迭代数量,本文采用一次迭代循环内进行2 次(父代、子代)目标值计算,利用reins 函数将子代目标值计算的优选个体代替父代目标值计算选用种群中的不良个体,形成新的种群,如此循环得到最优解。
5.3 优化结果
初始种群包含10 个个体,迭代次数为30 次,初始种群变异率为0.1,最大变异率为0.1,最小变异率为0.01,初始种群交叉率为1,最大交叉率为0.9,最小交叉率0.5,遗传算法迭代跟踪如图20 ~图22所示,变量参数结果如表1所示。
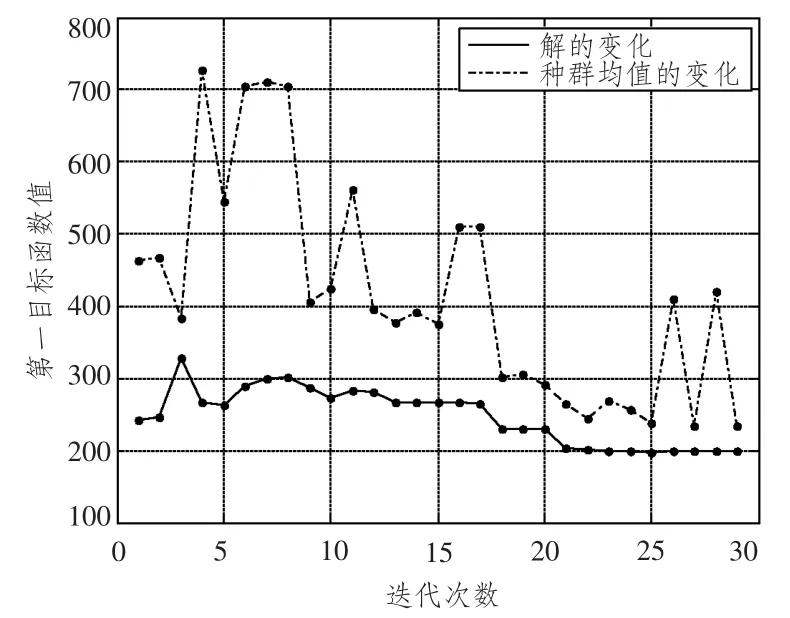
图20 子模型质量优化迭代图Fig.20 Optimization iteration of sub-model quality
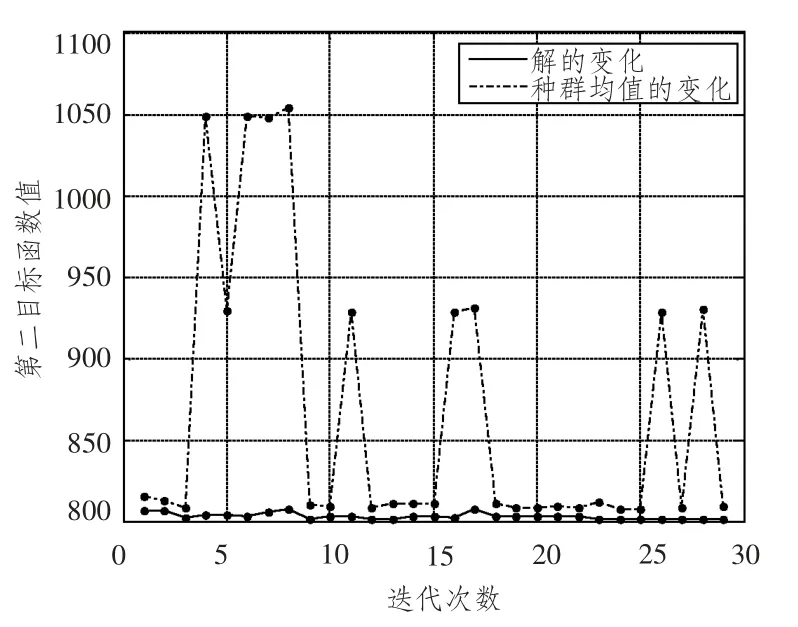
图21 子模型肘板最大应力优化迭代图Fig.21 Optimization iteration of sub-model biggest stress
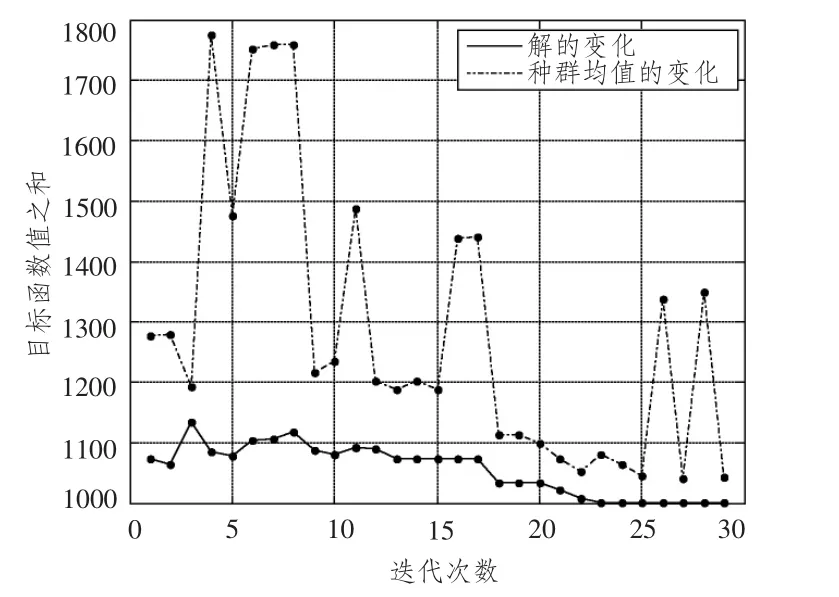
图22 子模型双目标优化迭代图Fig.22 Double objective optimization iteration of sub-model

表1 弧形肘板优化结果Tab.1 Optimization of curved bracket
性能指标如下:
质量:199.1 kg
最大未平均应力886.99 MPa;(肘板端部886.99 MPa);最大平均应力801.74 MPa(见图23)
子模型极限深度寿命:102.453=283 次(见图24)
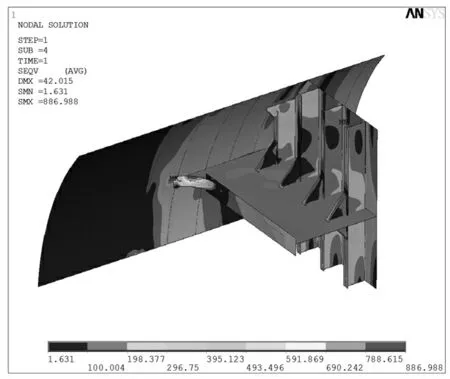
图23 4.9 MPa 弧形肘板优化后单元平均及未平均应力Fig.23 Element average and no average stress after optimization of curved bracket at 4.9MPa
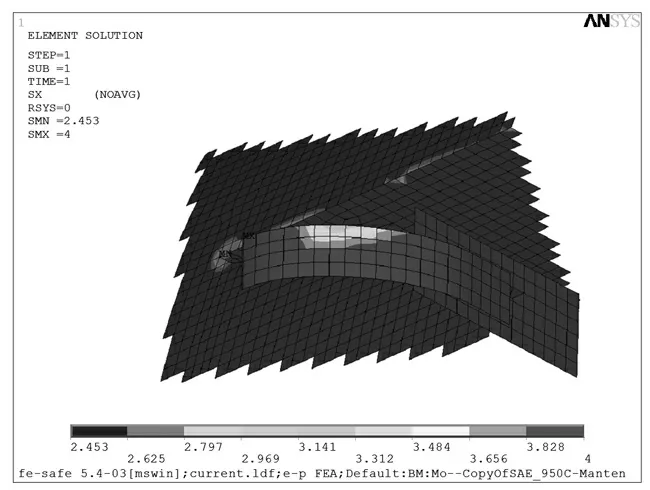
图24 4.9 MPa 弹塑性循环弧形肘板优化后疲劳寿命Fig.24 Elastic-plastic fatigue life after optimization of curved bracket at 4.9 MPa cycle
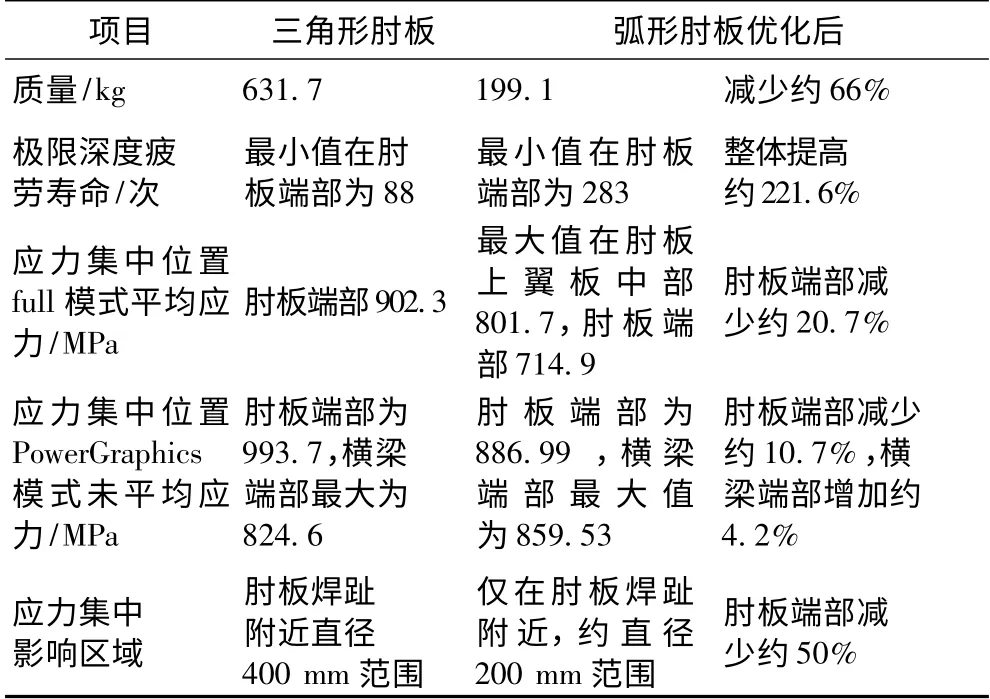
表2 肘板优化前后性能对比表Tab.2 Bracket performance comparison after optimization
6 结 语
本文根据假设舱壁结构尺寸,建立局部肘板结构参数化子模型,进行Matlab 与Ansys 联合遗传算法双目标优化,优化后弧形肘板相比三角形肘板质量大大减轻,疲劳寿命显著提高。总结如下:
1)参数化子模型通过自动导圆建立腹板弧线实现肘板腹板弧线椭圆与圆的拓扑优化。
2)子模型通过调用整体粗网格模型结果,计算规模减小,同时根据圣维南原理检验切割边界,肘板局部网格精细化的同时保证了计算精度。
3)讨论肘板局部应力应变历程及应力集中分布,采用局部应力应变疲劳设计理论,利用fe-safe 软件对三角形和弧形肘板进行弹塑性疲劳寿命对比。
4)成功实现Matlab 与Ansys 的联合遗传算法优化计算,基于Matlab 已有工具箱对遗传算法进行针对性改进,提高收敛速度。
5)利用fe-safe 疲劳软件基于三角形肘板应力应变结果进行初步疲劳分析,最后利用Ansys 参数化建模方法建立肘板弧形结构参数化模型,并与Matlab 中改进的遗传优化算法程序相互调用计算结果,优化得出质量与疲劳寿命两方面性能同时改进的椭圆形弧形肘板。
[1]夏伟,胡成,瞿尔仁.Ansys 子模型分析技术在处理应力集中时的应用[J].工程与建设,2006,20(2):92-94.
[2]高耀东,杨建鸣,汪建新.Ansys 子模型技术的应用[J].包头钢铁学院学报,2002,21(4):340-342.
[3]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2004:118-151.
[4]陈孝渝.潜艇和潜水器结构的低周疲劳[M].北京:国防工业出版社,1990,11:27-35.
[5]胡刚义,田旭军,杨振华,等.基于遗传算法的潜艇艏端耐压平面舱壁构架分级优化研究[J].舰船科学技术,2009,31(7):20-24.
[6]龚曙光,谢桂兰.Ansys 参数化编程与命令手册[M].北京:机械工业出版社,2010:1-81.
