顾及特征水深点距离重分配的反距离加权插值算法

王怀计，祝俊慧，胡莹，王瑞富

（山东科技大学 测绘与空间信息学院，山东 青岛 266590）

海底地形地貌的准确性表达对船只航行的安全性有着重要的影响，为了获得准确的海底地形地貌，为海洋学各种研究提供基础，需要对海底水深数据进行实测[1-6]，而实测的水深数据往往是离散点的形式，若某个区域的多波束测深数据缺少，且现有其他来源的水深数据的密度不能有效地反映海底地形地貌，通常需要通过空间内插方法增补水深点来得到足够多的海底地形地貌表面数据[7-8]。常用的空间插值方法有经典的反距离加权（inverse distance weighted，IDW）、自然邻域、样条函数法等，其中，IDW 算法以其原理简单而被广泛应用。

近年来，国内外学者对IDW 算法进行了许多研究，在算法的最优插值参数选择方面，张锦明等比较了该算法中权指数[9-10]、搜索点数[11]、搜索方向[12-13]等参数对插值误差的影响，得出了插值算法中的最优插值参数；在算法的应用方面，蒋伟达等利用IDW 对1958—2014 年埕岛7 个不同时期的水深点进行数据插值，分析各个时期的地形特征，得出了埕岛水下地形演变规律[14]；在算法的改进方面，何立恒等认为已知样本点在内插点的全圆方位上分布不均匀会对插值结果产生影响，提出了顾及夹角的改进IDW 算法，该方法能有效解决样本点分布不均对插值结果的影响[15]；樊子德等认为在不同的地形中人为调节权指数较为烦琐，提出了一种改进的IDW 算法，该方法能自适应地调整权指数，提高了算法的自适应性[16]。

通过上述对IDW 的分析可知，无论是在算法的插值参数选择方面还是在算法的应用和改进方面，IDW 插值的计算量问题都在于：若要求得一个待插值水深点的水深值，需要遍历所有已知水深点并进行距离的计算。在海量数据下，对数据点进行有效地索引可以减少计算量。另外，在算法改进方面，大多IDW 均假设空间过程具有平稳性，导致复杂海底地形的待插值水深点插值精度较低。因此，针对传统的IDW 方法在复杂海底地形适应性差的局限性，本文提出了一种顾及特征水深点距离重分配的反距离加权插值算法（distance-redistribution of characteristic depth points IDW，DCIDW），该算法首先对待插值水深点建立二阶相邻点，并在此基础上建立空间索引，利用二阶相邻点的个数自动调节搜索点数；然后对待插值水深点周围的样本水深点进行特征提取，特征水深点能反映样本水深点之间的相关性；最后根据距离分配因子进行距离重分配。该算法可在顾及样本水深点内部之间特征性的情况下，提高待插值水深点的精度。

1 特征水深点距离重分配DCIDW算法

经典IDW（classical IDW，CIDW） 算法假设待插值水深点的水深值与各个样本水深点之间的距离相关，通常采用距离平方的反比来定权，而忽略了海底地形的不平稳变化。在复杂海底地形中，CIDW 插值方法将所有的样本水深点视为同类别的点，不区分样本水深点之间的差异，此时相邻的水深点之间的水深值相差较大的情况如图1 所示。

图1 复杂海底地形传统水深插值误差示意图

根据反距离加权插值算法原理，待插值水深点A 的水深值由样本水深点B、C、D、E 以及其他周围样本水深点的水深值共同加权决定，因此A′的水深值应在最深点C 和最浅点D 之间。样本水深点B、C 与A 点相距较近，根据权函数要求，应赋给点B、C 较大的权，但是实际上，样本水深点D、E 对待插值水深点A′的影响更为重要，由于距离较远，所赋的权较小，导致待插值水深点与真实水深点之间存在较大的误差。图1 中的A′为忽略空间特征点D 和E 插值导致的结果，这不仅导致水深点不能反映真实的海底地形，而且会给航海安全带来重大隐患。因此，探索样本水深点中特征水深点的提取，进一步进行距离重分配，提高待插值水深点的真实性是非常必要的。

特征水深点的距离重分配算法主要包括特征水深点提取、特征点距离重分配、插值3 个步骤，详细流程如图2 所示。

图2 特征水深点距离重分配算法流程图

本文提出的特征水深点距离重分配算法，在样本水深点与待插值水深点之间距离之和不变的约束条件下，首先对实验区域内的样本水深点进行特征点提取，来反映样本水深点之间的空间相关性；然后提出距离重分配指标，对符合指标的待插值水深点进行距离重分配；最后构建一个顾及样本水深点之间空间属性的插值模型，提高特征点的权重，从而提高插值的精度。

1.1 特征水深点的提取

海底水深点的离散性造成了其空间关系分析上的复杂性，Delaunay 三角网根据离散点之间的相互关系，对离散点水深值的深浅进行描述。特征水深线是对水深点之间坡向关系的描述，选取局部区域内的相对浅点来反映相邻水深点之间的地形变化情况，特征水深点的数量越多，则地形震荡趋势越明显。基于上述原理，本文首先分析离散点之间的空间关系，然后构建特征水深线，并在此基础上，完成特征水深点的选取。

本文在对离散的水深点构建Delaunay 三角网的基础上，对离散的水深点构建特征水深线，根据特征水深线上各点之间的水深关系，提取出特征水深线上的特征水深点。特征水深线的提取是根据三角网之间的拓扑关系，递归追踪相邻点中的最浅点，依次连接各浅点，形成的过渡虚拟连接线。其能为特征水深点的提取提供判断依据，因此特征水深线是一种用来定义水深点之间关系的概念线。在特征水深线的基础上，对特征水深线上的水深点进行分析，比较线上各点的左右相邻点的深度差，进而选取特征水深线上的相对浅点作为特征浅点。

本文算法对特征水深点进行距离重分配的前提是样本水深点中的特征水深点的提取，该过程的主要任务是将离散的样本水深点结构化，判断样本水深点之间的空间关系，获取特征水深点[17-18]。离散的样本水深点不能反映各样本水深点之间的相关性，对离散的样本水深点构建Delaunay 三角网是建立点群空间相关性常用的方法之一，它是一系列相邻、不重叠的三角形构成的三角网，根据三角网之间的空间特性和拓扑关系，能有效地表达海底地形起伏形态[19]。

根据三角网之间的拓扑关系，对所有已知样本点递归追踪一阶相邻点中的最浅点，生成多条特征线，记录每一条特征线上的特征样本点。特征水深线的提取如图3 所示。

图3 水深特征线生成过程

特征水深点的提取过程如下：

（1） 单条特征线的提取。对样本水深点构建Delaunay 三角网，将三角形存入数组TIN；以全局水深最浅点Pmin为起始点，将Pmin存入数组PL；搜索起始点的相邻点，找到相邻点中与起始点深度差最小的点PN，追加存入PL。PL内的点不会再被搜索到；以PN为起始点，重复上述操作，直到找不到相邻点为止。按序连接PL中的点，得到一条特征线；

（2）所有特征线的提取。找到剩余未被记录的水深点中的最浅点，作为起始点，重复步骤（1）中的操作，直到所有的点都被搜索到为止，最终得到若干条特征线。

（3）特征水深点的提取。特征水深点是特征水深线上的特征浅点，能反映局部区域内的水深差值情况，特征水深点的提取过程如图4 所示。

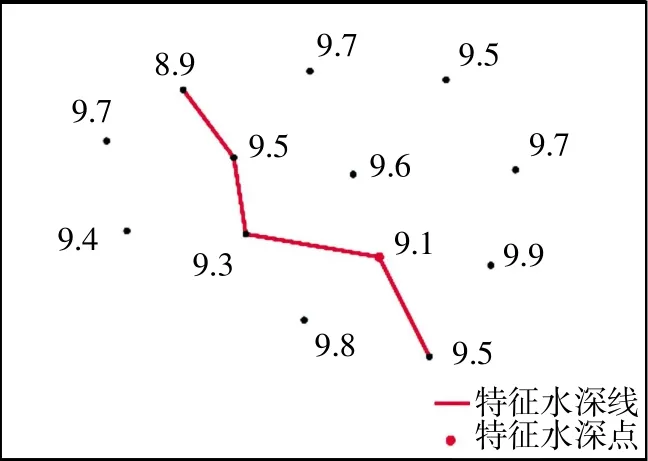
图4 基于特征水深线的特征水深点提取过程

具体步骤为：①设特征线上水深点数为n，记为P1，P2，…，Pn，点的水深值记为H1，H2，…，Hn；②若Hi＜Hi-1且Hi＜Hi+1（i=2，3，…，n），则Pi是水深浅点，存入数组Pc；③若连续多个水深点的深度值相同，则与连续起点的前一点的水深值和连续终点的后一点的水深值进行比较，选取Pi和Pi+1中的一点作为特征点；④重复上述步骤，直至特征水深点提取完成。

1.2 基于特征点的距离重分配

CIDW 插值算法不考虑周围的样本水深点的特征性，只简单地考虑距离倒数的平方对权函数的影响。本文在提取特征点之后，在所有样本水深点到待插值水深点的距离和不变的约束下，量化比较待插值点的二阶相邻点中特征点的个数占比与特征点距离之和与总距离占比，实现对复杂的海底地形特征点的距离重分配。

（1）二阶相邻点的选择。待插值点的二阶相邻点选择的实质为空间邻近分析问题，Delaunay 三角网作为空间邻近分析工具之一，广泛应用于空间数据聚类和空间邻近关系探测[20]，故本文应用Delaunay 获取待插值点周围的一阶相邻点[21]，在一阶相邻点的基础上，获取待插值点的二阶相邻点，其中包含特征点和非特征点，样本点均匀地分布在待插值点的周围。

（2）特征点距离重分配。根据待插值点二阶相邻点中特征点的个数Nfeature和每个特征点到待插值点的距离dfeature_i，计算得到待插值点的二阶相邻点中特征点个数占比Ratio_N 和特征点距离占比Ratio_D，从而可以获取每个待插值点是否需要距离重分配判断指标，计算公式如下：

从上式提出特征点距离重分配指标：若Ratio_D ＜Ratio_N 表明特征样本点距离待插值点较近，特征点对待插值点的权重受地形影响较小，因此无需对特征点的距离进行重分配；若Ratio_D ≥Ratio_N 表明特征点距离待插值点较远，特征点对待插值点的权重受地形影响较大，按照阈值的比例对特征点的距离重新分配，分配公式如下：

特征样本点的距离重分配算法具体步骤如下：①获取待插值水深点的一阶相邻点，在一阶相邻点的基础上获取待插水深点的二阶相邻点n；②获取待插值水深点与二阶相邻点的距离di；③比较阈值Ratio_N 与Ratio_D 大小，判断是否需要对特征点的距离重新分配；④重复上述步骤，直至待插值水深点距离重分配完成。

样本点的距离和个数是影响待插值点精度的两个重要因子，本文引入了特征点距离占比和特征点个数占比两个指标，若特征点距离占比大于特征点个数占比，表示其相较于其他样本水深点与待插值水深点之间的距离较远，因此用特征点个数占比代替特征点重分配之后的距离占比，能使特征水深点与待插值水深点之间的距离变近，在二阶相邻点总距离不变的约束下，其他样本水深点重分配之后的距离和为总距离与特征水深点重分配距离的差值。

1.3 插值

由于待插值水深点的二阶相邻点中可能存在特征样本点距离待插值水深点较远，但对待插值水深点影响较大的情况，特别是距离待插值点的水深值与较近的其他水深点的水深值差别较大会使CIDW插值算法得到的插值结果与真值相差较大。基于此，本文在CIDW 插值算法的基础上，对每个特征点的距离重新分配，计算公式如下：

式中，dfeature_i为每个特征水深点与待插值水深点之间的原始距离，d′feature_i为每个特征水深点与待插值水深点之间的重分配距离，d′others_i为每个其他水深点与待插值水深点之间的重分配距离。

基于上述公式，本文提出了一种顾及待插值水深点的二阶相邻样本点中特征样本点的IDW 插值模型：

2 实验对比分析

2.1 特征水深点的选取

本文实验数据来源于夏威夷茂伊岛附近的机载激光雷达测深数据，特征水深点的提取实验过程如下。

（1）本实验选取区域内部分水深点作为实验数据，包括待插值水深点以及其周围的已知水深点，用于构建Delaunay 三角网，构建结果如图5 所示。

图5 三角网构建

（2）提取特征水深点。根据水深特征线构建方法，对整体水深点构建水深特征线，构建特征水深线的目的是为了分析已知样本水深点之间的关系，提取样本水深点中的特征水深点。所选取的部分水深点构建结果如图6 所示。

图6 特征水深线和特征水深点提取结果

2.2 基于特征水深点的样本水深点的距离重分配

（1）在已提取的特征水深点基础上，首先对待插值水深点构建二阶相邻线，得到待插值水深点的二阶相邻点，结果如图7 所示。

图7 待插值水深点的二阶相邻点

（2）按照待插值水深点的二阶相邻点中特征水深点与所有二阶样本水深点的个数比值和特征水深点与所有二阶样本点的距离比值进行分析，待插值水深点与样本水深点之间的距离需要进行重分配，待插值水深点与样本水深点之间的距离在总距离之和不变的约束下，对各个样本水深点的距离进行重新分配，分配过程示意图如图8 所示。

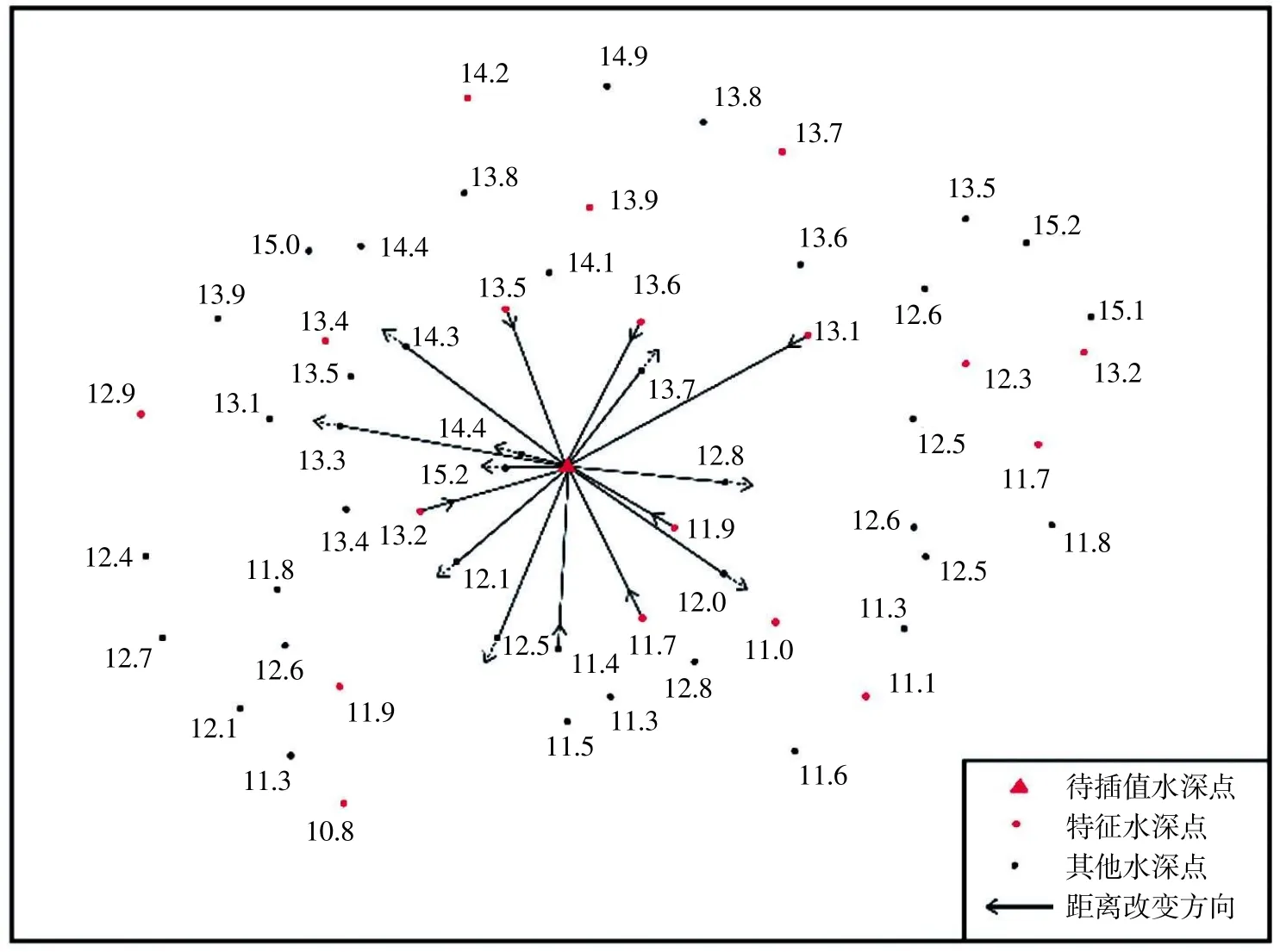
图8 样本水深点距离重分配示意图

（3）对待插值水深点与样本水深点之间的距离进行重分配之后，按照式（7）对待插值水深点进行水深计算，待插值水深点与周围二阶相邻点的实际地形如图9 所示。

图9 待插值水深点实际水下地形图

图中待插值水深点的实际水深值为13.9 m，蓝色点为待插值水深点的二阶相邻点中其他水深点，与待插值水深点之间的平面距离分别为15.6 m、4.9 m、5.9 m、18.0 m、21.5 m、17.5 m、25.6 m、23.3 m、22.6 m、22.8 m，其他样本点与待插值水深点之间重分配的平面距离分别为16.9 m、5.3 m、6.4 m、19.5 m、23.3 m、19 m、27.8 m、25.3 m、24.5 m、24.7 m，为更好地表现出分配之后的距离变化，其他水深点的距离重分配结果如表1 所示。

表1 其他水深点的距离重分配表

红色点为经过特征提取之后的特征水深点，与待插值水深点之间的平面距离分别为13.5 m、30.0 m、26.3 m、22.0 m、15.6 m、23.4 m；根据本文提取的样本水深点距离重分配方法，特征样本点与待插值水深点之间重分配的平面距离分别为11.9 m、26.5 m、23.3 m、19.5 m、13.8 m、20.7 m，为更好地表现出分配之后的距离变化，特征水深点的距离重分配结果如表2 所示。

表2 特征水深点的距离重分配表

依据CIDW 算法，权函数的幂指数为2，周围水深点数为12，P 点的内插值为14.05 m。依据本文提出的DCIDW 插值算法，利用式（7） 计算P点的内插值为13.95 m，此值与实测水深值更接近，减弱了样本水深点变化不均匀对内插水深值的影响。

为进一步验证特征采样点的距离重分配算法的可行性，对本文选取的整体海区的样本水深数据进行实验，研究区域样本水深数据共1077 组，其中862 组作为训练集样本进行建模，215 组作为测试集样本进行验证。研究区域平均水深为16.37 m，最大水深为29.48 m，最小水深为8.49 m。

本文选取的215 组待插值水深点中，有105 组进行了距离重分配，110 组未进行距离重分配，插值结果有两类情况，如图10 所示。图10（a）中由于实际水深周围地形的复杂性，本文提出的DCIDW插值方法能有效接近实际水深值，相较于CIDW 方法能有效逼近真实海底地形，图10（b）中本文提出的DCIDW 插值算法相较于实际水深更浅，而CIDW 算法相较于实际水深更深，给航行安全带来隐患。将本文DCIDW 算法和CIDW 算法的插值结果与真实水深作差（图11），分析可知，本文提出的方法在复杂海底地形情况下相较于传统方法能保证待插值水深点的内插质量。

图10 插值水深结果分类图

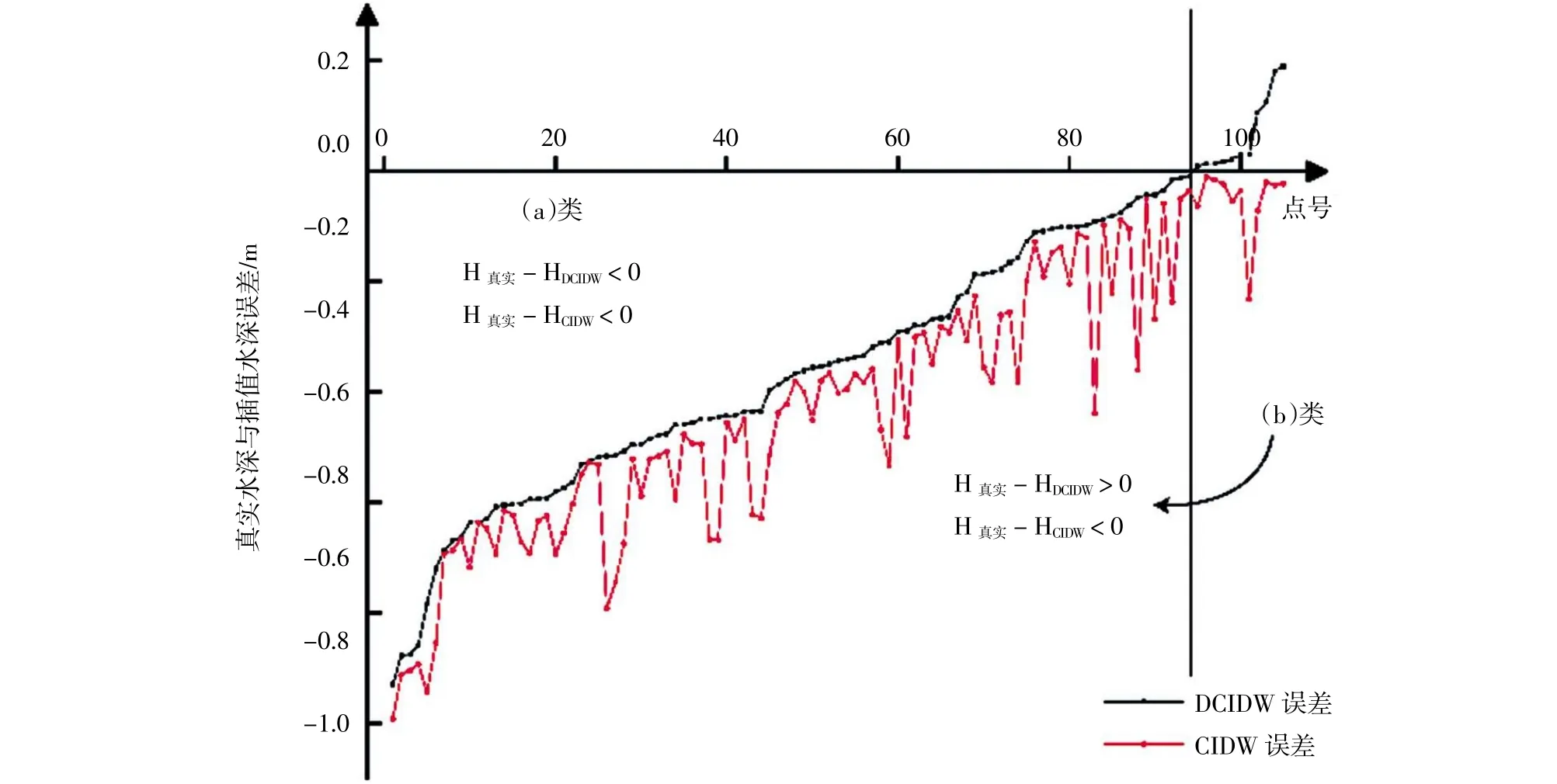
图11 插值水深与实际水深误差示意图

将本文提出的算法与CIDW、自然邻近点插值（natural neighbor interpolation，NNI）、样条函数插值（spline function interpolation） 算法进行对比分析，其中CIDW 参考点数量选取12 个，本文提出的算法待插值点的参考数量为二阶相邻点，两种IDW 插值算法幂指数均取值为2，待插值点从样本点中随机筛选，实验采用交叉验证方法验证算法的误差精度，选取平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）来表达待插值点插值结果的绝对误差，相对误差（relative error，RE）来表达待插值点插值结果的相对误差。

实验结果如表3 所示。为了直观地显示4 种水深插值方法的实验结果误差，将4 种水深插值方法对应的精度评价指标MAE 和RMSE 绘制成柱形图，如图12 所示。

表3 四种水深插值方法的实验结果

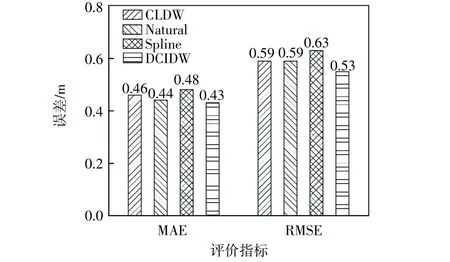
图12 四种水深插值方法实验结果

分析图12 可以发现，CIDW、NNI 和Spline 插值算法的MAE 分别为0.46 m、0.44 m、0.48 m，NNI 插值精度比CIDW、Spline 插值算法都要高，而本文提出的顾及特征水深点距离重分配DCIDW插值算法的MAE 在4 种算法中最低，为0.43 m；CIDW、NNI 和Spline 插值算法的RMSE 分别为0.59 m、0.59 m、0.63 m，Spline 插值算法的RMSE为0.63 m，相比较于CIDW、NNI 两种插值算法，插值精度较低，而本文提出的顾及特征水深点距离重分配DCIDW 插值算法的RMSE 在4 种算法中最低，为0.53 m。通过对图12 分析可知，本文方法在精度上优于其他三种方法。相比于其他方法，本文方法进行待插值水深点插值时进行了特征提取和距离重分配，降低了空间非平稳变化的影响，插值精度有所提高。

3 结语

本文针对CIDW 在复杂海底地形适应性差的局限性，提出了一种顾及特征水深点距离重分配的反距离加权插值算法。该算法顾及样本水深点的周围特征点对插值的影响，根据特征点距离分配因子对距离重新分配，从而提高了反距离加权插值算法在复杂海底地形中的精度。最后通过实测水深数据实验验证了本文方法的优越性和可行性，该方法能有效地减弱在待插值水深点插值过程中样本水深点邻近点水深值分布不均匀对内插值的影响，与已有方法相比提高了插值结果的精度。

当然，本文仅针对一些典型区域进行了验证，对于其他地形变化复杂的区域，本方法还需要进一步的研究。另外，本文仅单方面地考虑了特征水深点对待插值水深点水深值的约束，对于待插值水深点与等深线、地形线不同因素相互间的协调约束，有待进一步地探索。