船舶动力定位系统多模型自适应融合滤波

杨金节，俞孟蕻，李晨曦，宗洪亮

(江苏科技大学 计算机学院，江苏 镇江212003)

0 引 言

由于传统锚泊系统不能经济地在深水区实现驳船，动力定位系统(DP)应用于海上钻井平台，出现在20世纪60年代。为防止响应于波频组件的过度控制活动，减少动力系统部件的机械磨损，估计值进入DP 反馈控制回路前应采用滤波技术。在实践中，船舶位置和首向的测量不仅与传感器的噪声有关，也与由风、浪、流引起的有色噪声有关。因此，要达到滤波效果，必须滤除位置和首向测量信息中的噪声和高频信号［1-2］。

基于模型的扩展卡尔曼滤波器(EKF)广泛应用于现代工业船舶动力定位系统中，然而，由于其对模型的严格要求，实际系统的模型稍有变动都会造成滤波器的状态估计值偏离系统的真实状态，出现滤波发散现象，系统的全局指数稳定性(GES)不能被保证。

本文在前人对DP 开创性工作的基础上，以船舶动力定位系统为滤波模型，该模型仅依赖于船舶的位置和首向测量，基于采纳的模型提出一种多模型自适应融合滤波算法，以实现滤波，得到船舶的有效位置和首向信息。

1 滤波和船舶建模

1.1 滤波

动力定位系统的主要目的是在一定的范围内保持船舶的航向和位置。通过设计适当的滤波器来有效实现最好的中央航向和位置估计。一般情况下，船速的测量是不可靠的且船舶的位置和方向的测量存在着不同噪声的破坏，因此估计的速度必须通过状态观测器从位置和首向测量干扰中计算出。动力定位系统中只有缓慢变化的扰动应被推进系统抵消，而由一阶波浪引起的振荡运动不应进入反馈控制回路。所以，DP 控制系统应只对作用在船舶上低频作用力的影响做出反应。如前所述，滤波技术被利用于滤除位置和首向测量信息中的高频成分和噪声，得到船舶低频运动的状态估计值。典型的滤波框图如图1所示［3］。

图1 滤波框图Fig.1 The block diagram of filtering

1.2 船舶低频运动模型

在实际工程应用中，只需要考虑首摇、横荡、纵荡3 个方向，船速以船舶的重心为参考点。根据牛顿第二定律分析船在首摇、横荡、纵荡3 个方向的受力，得到如下的低频运动方程［4-5］:

式中:η=［x，y，ψ］T为在固定坐标系中船舶的位置(纵荡、横荡)和首摇角度;v=［u，υ，r］T为在随船坐标系中船舶的速度(纵荡、横荡)和首摇角速度;J(ψ)为固定坐标系和随船坐标系的转化矩阵;τcontrol为船舶自身推进系统产生的纵荡、横荡方向上的合力和艏摇方向的合力矩;τwind为风力和风力矩;偏差项b ∈R3为未建模的外界环境干扰力和力矩，是由风、浪、流综合在一起形成的定常或缓慢变化的矩阵。

考虑横荡和首向方向的耦合，有

船舶动力定位过程中，因航速较低，一般不考虑横荡和首向方向的耦合，故

在动力定位过程中，有

式中:ηp为随船坐标系中船舶的位置(纵荡方向、横荡方向)和首摇角度。由于船舶在首摇方向的转动较慢，因此，可近似取。又根据bp≈JT(ψ)b，bp为随船坐标系下纵荡、横荡和首摇3 个方向上未建模的外界环境干扰力和力矩。于是式(1)～式(3)可写为:

其中wE为高斯白噪声，表示系统模型的偏差信息。将式(5)～式(7)转化为状态空间的形式如下:

1.3 船舶高频运动模型

假设不考虑船舶运动在纵荡、横荡和首摇3 个自由度上的耦合，通过波谱密度拟合，船舶在3 个自由度上的高频运动模型可以近似地表示为带有附加阻尼的二阶谐波振荡器［6］:

式中:Kω=2ζω0σω，ζ 为相对阻尼系数，一般可取ζ=0.1;均方差，由谱分析的相关理论，σω和有义波高的关系可近似为:

将式(9)转化为时域的形式，得

转化为状态空间的形式:

1.4 滤波方程

根据以上建立的船舶低频和高频模型，建立3个自由度方向上船舶动力定位滤波器所需要的状态方程和量测方程如下:

以纵荡方向为例对方程进行推导，U 为船舶自身产生的合力、合力矩项与风对船舶产生的风力、风力矩项之和;ω 为纵荡方向未建模的海洋环境因素;υ 为纵荡方向的量测噪声。ω和υ 为相互独立的高斯白噪声;Y 为所测纵荡方向的位置信息。其中，

当系统噪声具有时变特性时，系统方程式(14)可以改为如下形式:

式中η和ξ 为相互独立的高斯白噪声，具有未知时变噪声统计特性。

2 自适应融合滤波算法

基于系统模型的Sage-Husa 滤波器和强跟踪滤波器(STF)都是以卡尔曼滤波方程为基础建立的，各有优缺点，前者的滤波精度高但鲁棒性差，后者的自适应能力强但滤波精度低。本文运用一种多模自适应融合滤波算法将两者有机结合，每个系统模型对应不同的滤波器，且并行工作。各滤波器的输入是模型条件概率转移后的修正值，系统的最终输出是各模型滤波器输出状态估计的加权融合［7］。

2.1 Sage-Husa 滤波算法和STF

Sage-Husa 自适应滤波算法是在利用观测数据进行递推滤波的同时，通过时变噪声统计估计器，实时估计和修正系统过程噪声和观测噪声的统计特性，从而达到降低模型误差，抑制滤波发散，提高滤波精度的目的。方程描述如下［8］:

强跟踪卡尔曼滤波算法是通过牺牲一定的滤波精度来换取滤波器的稳定性和收敛性，通过在系统过程状态向量估计误差协方差阵前乘以多种次优渐消因子λk来实现，如下式:

式中:αi≥1，i=1…n，由先验信息确定;0 ＜ρ ≤1为遗忘因子，通常取ρ=0.95。

2.2 自适应融合滤波算法

受外界环境的干扰，船舶在不同时刻对应系统的模型有所不同，设系统的模型集为M={m1，m2…mL}，模型的转换符合一阶马尔科夫过程，从mj(k)到mi(k+1)的转移概率由先验知识获得，记为tji，且:

从传感器获得测量信息后，mj(k)到mi(k+1)的模型预测概率为βj/i(k)，且:

式中:βi(k)=p{mi(k)/Yk}为模型mi在k 时刻系统匹配模型概率，系统的测量信息集Yk={Y(1)，Y(2)，…，Y(k)}。已知测量信息Y(k)，则基于模型mi(k)的滤波输出残差为:

则输出残差的协方差为:

由理论分析可得，若当所建船舶模型与实际情况相符，则εi(k)=0，方差为Si(k)的高斯白噪声，k 时刻mi(k)的模型匹配似然函数可以表示为:

可得模型的概率更新方程为:

为了便于分析，取L=2，由前面所述可得，M={m1，m2}，m1代表模型(14)，m2代表模型(15)，模型m1和m2分别采用STF和Sage-Husa 滤波器进行滤波。自适应融合滤波器的结构如图2所示［9］。

图2 滤波器结构图Fig.2 Architecture of the filter

由图2 可得:

1)基于模型m1和m2的滤波器输入初值分别为:

其中P1(k)和P2(k)为状态误差协方差。

2)滤波器输出残差协方差分别为:

3)滤波器的输出:

结合公式可得状态估计值^x(k)为模型m1和m2的滤波状态估计的加权融合:

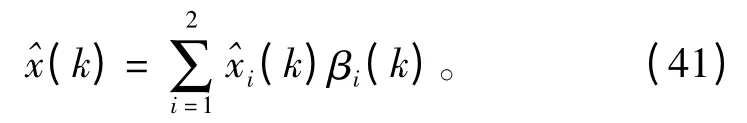
3 仿真分析

由上文分析，m1代表模型(14)，m2代表模型(15)。对模型进行初始化:

式中:β1(0)和β2(0)分别为模型m1和m2的初始模型概率。

在无约束条件下，t12和t21是模型m1和m2的转移概率，值较小;t11和t22分别为模型m1和m2的不变概率。

本文以某大型海洋工程船舶为研究对象，海面平均风速为11 m/s 左右，船舶处于对水低速航行状态、空载排水量为21 890 t，满载排水量为42 180 t。在船舶空载和满载状态下分别对纵荡、横荡和首向进行多模自适应融合滤波，效果图如图3 ～图4所示。

图3 空载滤波图Fig.3 The filtering effect diagram of empty load

由图3 ～图4 可以看出，该滤波器能够有效地滤除噪声和高频信号的干扰，估计出船舶低频位置(纵荡、横荡)信息和首向角度。

图4 满载滤波图Fig.4 The filtering effect diagram of full load

4 结 语

由于海洋环境恶劣，船舶系统模型存在着很大的不确定性，而STF和Sage-Husa 滤波器在克服系统模型不确定上各有优缺点。本文设计的自适应融合滤波器既有STF 对突变状态的强跟踪能力，以及鲁棒性强的优点，又有Sage-Husa 滤波器状态估计精度高及对噪声变化的自适应能力。仿真表明，该滤波算法能有效解决海洋工程船舶的滤波问题。

［1］SØRENSEN A J.A survey of dynamic positioning control systems［J］.Annual Reviews in Control，2011(35):123-136.

［2］NGUYEN T D，SØRENSEN A J，QUEK S T.Design of hybrid controller for dynamic positioning from calm to extreme sea conditions［J］.Automatica，2007，43(5):768-785.

［3］SØRENSEN A J.Lecture notes on marine control systems［R］.Norwegian University of Science and Technology，Tech.Rep.Report UK-11-76，2011.

［4］贾欣乐，杨盐生.船舶运动数学模型［M］.大连:大连海事大学出版社，1999:18-19.

［5］JENSEN G A，OMC N S，NGUYEN T D，FOSSEN T I.A nonlinear PDE formulation for offshore vessel pipeline installation［J］.Ocean Engineering，2010(37):365-377.

［6］JENSSEN S S，BALCHEN N A.Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control［J］.IEEE Transaction on Automatic Control，1983，28(3):332-338.

［7］徐肖豪，高彦杰，杨国庆.交互式多模型算法中模型集选择的分析研究［J］.航空学报，2004，25(4):352-355.

［8］付梦印，邓志红，张继伟.Kalman 滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2010:108-120.

［9］王小旭，赵琳.自适应融合滤波算法及其在INS/GPS 组合导航中的应用［J］.宇航学报，2010，31(11):2506-2508.