数形结合方法在高中数学教学中的应用

张秀莲

摘 要： 数形结合的实质是把直观图像和数学中的抽象语言结合在一起，使形象思维与抽象思维有机结合，并将抽象转化为直观，化难为易。数形结合是高中数学教学的本质特点之一，将数形结合运用在高中数学教学中，可以使学生的理解能力、分析能力、观察能力、综合能力得到提高，为学生的数学学习提供有利条件。本文主要对数形结合法在高中数学教学中的应用进行分析。

关键词： 数形结合 高中数学教学 应用

1.引言

将数形结合法运用在高中数学教学中，可以使学生绕过数学学习中的障碍，脱离各种繁琐的理论推导，根据图形数学函数进行理解并进行使用。数形结合可以将几何与代数问题结合起来，让代数问题得到较好的诠释，使数学中复杂的问题得以明了化、简单化。

2.将数形结合运用在高中数学教学中的作用

将数形结合运用于高中数学教学中的具体作用有：第一，数形结合的运用可以帮助学生发展形象思维，提高学生对数学的学习兴趣，增强学生学好的信心。因为数学具有独特的抽象性、形式化、符号化等特点，让学生对数学产生一种冰硬、生冷的感觉，所以导致学生对学习数学的兴趣较低，产生厌恶、枯燥的情绪[1]。将数形结合运用在高中数学教学中，可以降低学生学习的难度。在数学教学中，可以利用数形结合为代数提供相应的几何模型，从而将问题本质直观、形象地揭示出来。该方法减轻了学生的学习负担，激发出学生对数学的学习兴趣。第二，数形结合有利于学生对现代思维、意识进行树立。数形结合的有效运用可以帮助学生对问题进行多角度、多层次的分析，让学生形成放射性思维。且数形结合在一定的程度上可以引导学生将静态思维与动态思维结合起来，通过联系、变化、运动的观点对问题进行思考，进而对事情的本质进行把握。另外，数形结合可以使形象思维和抽象思维相结合，从而给学生辩证思维的形成创造有利条件。

3.高中数学教学中数形结合的具体运用

3.1抽象函数中数形结合的有效运用

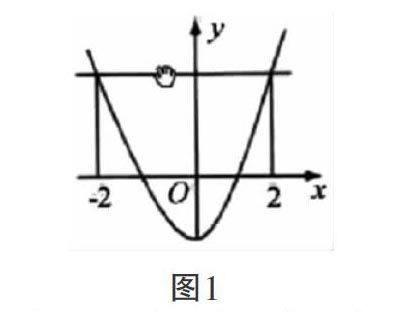
将数形结合运用在高中数学教学中，可以使学生在理解函数知识时更容易。在高中函数教学中，往往会碰到许多和函数性质有关的命题，学生在理解过程中会觉得比较困难，但是如果将数形结合运用在其中，学生就可以根据数形结合的特点解决问题。如在讲解偶函数时，假设y=f（x）这个函数是偶函数，且其在区间（-∞，0）上为减函数，f（2）≤f（a），让学生判断出a的实际取值范围。在面对此类抽象的问题时，如果直接运用数学推导对其进行解决就会显得非常困难，但是根据图形解决这种抽象的问题就会比较容易[2]。在解决该问题的过程中，首先应画出相应的图形，如图1。

图1

因此，通过图1就可以看出该函数是偶函数，而且根据题目中的条件可以得出a的取值范围。面对此类抽象的函数问题时，若能够直接将函数图形画出来，只需根据偶函数的对称定律就能够直接得出正确答案。

3.2将数形结合运用在函数性质的记忆中

高中数学中的许多知识都比较繁琐、抽象，学生可以根据数形结合解决这些抽象的问题，帮助学生对函数知识进行记忆、巩固。如高中数学中三角函数的运用，在处理此类问题时，学生必须牢记tanx、cosx、sinx相关的函数性质，在记忆过程中学生可以运用数形结合的方法，这样不但可以节省时间，而且轻轻松松就可以将其全部记住。学生对sinx函数的相关性质进行记忆时，若将sinx的具体图形画出来，学生就可以很容易地区分清楚sinx的单調区间、周期、奇偶性、对称性；就是说学生只要将sinx的图形记住，就可以完全将sinx的性质记住。

3.3解决函数问题中数形结合的具体运用

从任何一个阶段的教学教学宗旨来看，其都是为了对学生解决实际问题的方法进行锻炼，高中数学教学中将此类问题称作应用题。在解决应用题的过程中，并不是根据相关数字就可以使问题得到解决，也不是单靠一幅图就可以解释清楚的。需要学生利用具体图形将问题核心展现出来，再利用数学推导才可以得出正确答案[3]。如在许多求值域、最值的函数题目中，上述问题就会体现出来，但是学生利用数形结合对其进行处理就可以很快得出正确答案，这样还可以使学生探索的精神得到激发，从而更积极主动地学习数学知识。

4.结语

将数形结合运用在高中数学教学中可以使学生解题思维得到不断发展，增强解题能力，对学生数学思维的发展也有重要影响。数形结合可以利用几何问题映射代数问题，使代数问题与几何问题相互转换，使学生将抽象思维和形象思维结合起来，降低学生解题的难度。

参考文献：

[1]成彦盛.高中数学教学中数形结合方法的有效应用[J].教育界，2014，46（20）：357-358.

[2]农忠勇.“数形结合”思想在高中数学教学中的重要作用[J].读写算（教育教学研究），2013，38（30）：457-458.

[3]洪榕波.“数形结合”思想在高中数学中的应用[J].华章，2013，35（12）：468-469.