融合局部和非局部信息的自适应贝叶斯分割方法

2014-11-18王青平赵宏宇吴微微付云起袁乃昌

电子与信息学报 2014年4期

王青平赵宏宇吴微微付云起袁乃昌

(国防科技大学电子科学与工程学院长沙 410000)

1 引言

合成孔径雷达 (SAR) 系统具备全天候、全天时的成像能力，还有一定的穿透性，已被广泛应用于军事和民生领域[1]。SAR图像分割是解译和识别的重要部分，可以提供图像信息的整体架构[2]。近年来，基于各种理论提出了大量的分割方法，但还没有哪一种方法能够有效地分析、检测SAR图像中所有的结构特征。

基于马尔可夫随机场(Markov Random Field,MRF)的贝叶斯分割方法，可以有效地把像素间空间交互关系无缝地集成在影像的分割过程中，并能将上下文信息引入到图像的分割过程，具有较强的噪声抑制能力，成为目前的一个研究热点[3]。文献[4]利用 MRF模型完成了 SAR图像的分割；文献[5]在传统 MRF的邻域基团势函数基础上，引入了图像邻域中各个像素的强度差值以及像素之间的距离因子，使SAR图像的空间上下文信息得到了更加充分的利用。文献[6]将多分辨率技术从像素级扩展到区域级，结合区域多分辨率和 MRF模型，提出了一种新的分割方法，改善了多分辨率分割效果。文献[7]提出一种快速边缘追踪方法，在保持分割效果的前提下，极大地减少了非监督 MRF分割的运算时间。但传统的 MRF方法仍有一些缺陷，其先验模型只考虑了图像局部邻域信息，对于噪声污染严重的图像，鲁棒性不强；不能很好地描述边缘，分割效果欠佳，这是由于邻域中每个像素对中心像素的影响相同的假设条件并不合理。

本文借鉴近年提出的非局部概念[8]，针对 SAR图像包含乘性相干斑噪声，采用一种新的相似性测度定义，并基于这种测度提出了新的先验模型，将图像的非局部信息引入势函数定义中；新的势函数引入了高斯核函数，考虑了图像搜索窗中各个像素的惩罚不一致性，从而更加充分地利用了图像的上下文信息；并且考虑SAR图像分割过度平滑与结构保持的矛盾，在边缘区域自适应矫正，得到了更好的分割效果，其抗噪性与鲁棒性更强。

2 MRF图像模型

Markov随机场是文献[9]提出来的。大小为M×N的2维图像可以表示为一个方形网格。假设Y为S的观测场，X为S的标记场，y和x分别表示Y和X的一个实现。图像分割问题转化为通过观测场Y的一个实现y估计标记场X的一个实现x。在最大后验概率(Maximum A Posterior, MAP)准则下，要求标记场的后验概率最大，即

通常，定义标记场X为MRF(即满足正定性与Markov性)，Hamersley-Clifford定理[9]确定了Markov随机场和Gibbs随机场之间的等价关系，从而给出了Markov随机场的先验概率：

其中iN表示i的邻域位置，表示随机场基于局部邻域能量，T为温度常量，通常设为 1。从而，MRF图像分割方法可以转换为求式(3)的能量函数最小时的标号场X的组合优化问题：

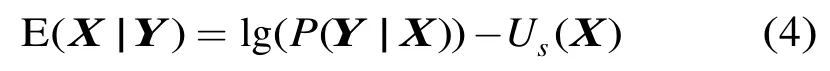
3 改进的非局部贝叶斯分割方法

3.1相似性测度

事实上，当图像被噪声严重污染时，邻域像素也会被污染，这时，像素的局部空间信息则会失去其在分割中应有的积极作用。近年提出的非局部概念[8]，在图像中寻找与特定像素具有相似邻域结构的其它像素，并利用其获得当前像素的空间信息。

因而，如何稳定描述两个含噪像素点的相似性非常重要。文献[8]利用欧氏距离介绍了一种像素相似性测度，并设计了一种有效且稳定的非局部平均滤波器。其像素点相似性测度为

然而，对于SAR图像，其观测值Y可以描述为

其中X表示无噪声值，Z为相干斑噪声，对于这种乘性噪声，文献[10]给出了详细推导，证明式(5)失去了其有效性及鲁棒性。

为了解决这一难题，文献[11]提出一种相似性测度定义方法，它假设SAR图像噪声为加性噪声和乘性噪声的混合，且乘性噪声服从高斯分布。基于这种假设，皮尔逊距离被用来度量两个像素块的相似度。文献[10]改进了一种相似性测度的迭代逼近方法，这种方法采用先验知识，显著提高了相似性测度的精度。文献[12]假定每一像素周围被一小块同质区域所包围，在这一区域中定义了一种新的比率距离及其概率密度函数映射，并证明了这种比率距离映射对乘性噪声的有效性及鲁棒性，取得了显著进展。其相似性测度为

其中L为SAR图像的等效视数(ENL), M为邻域窗内所有像素点数，()Γ⋅为伽马函数。这种测度比较的不只是单个像素点之间的灰度，而是将整个邻域结构考虑在内，针对乘性噪声模型，将像素块之间的差异由差值转化为比值，并映射到其概率密度函数，对相干斑噪声的抑制具有极大的优越性[13]。图1中，“*”标记为中心像素点及其邻域，“o”标记为与中心像素块相似的像素块，而“×”标记处的灰度值虽然与中心像素点相同，但二者并不相似。

3.2 非局部贝叶斯分割

传统用来描述MRF的Potts模型，只考虑二元势函数，定义为

其中β是对应的势团参数。这种模型过于简单，由于只考虑了邻域像素点的影响，无法有效抑制相干斑噪声；而邻域中每个像素对中心像素影响相同的假设条件不能很好地描述边缘，分割效果欠佳。因此，在式(7)，式(8)定义的像素相似性测度基础上，重新定义改进的标记场势函数如式(10)，使其融入非局部信息，并且满足相似度较小、距离较远的像素对中心像素的影响较小，反之较大。

从而，由式(10)可得随机场X的先验能量为

其中xL为以像素点x为中心的固定尺寸的方形搜索窗，δ为狄拉克函数，xN 是像素x的邻域，G是标准高斯核函数。

图1 与中心像素点相似的像素块

图2 边缘区域未矫正非局部贝叶斯分割

3.3 边缘区域自适应矫正

图2为非局部贝叶斯分割后的结果，测试图像采用Radarsat-1卫星获取的基隆港口SAR 图像(C波段，4视，分辨率10 m)，可以看出，非局部贝叶斯分割方法虽然使分割抗噪性更强，但也使得边缘区域过于平滑，细节特征不明显甚至丢失。因而，需要在边缘部分加以矫正，以保持其几何结构。

首先，可以采用基于变分系数(CV)阈值的方法[14]找出边缘区域，其定义为

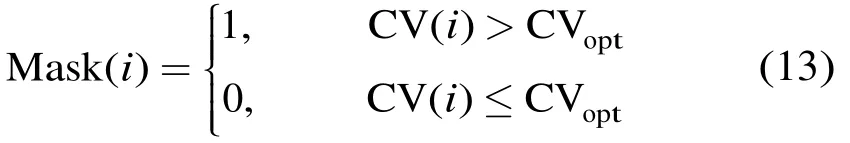
其次，对边缘区域加以矫正。在CV值较小的平坦区域，为了对相干斑噪声有很好的抑制效果，应选择较大的搜索窗及势团参数，以增大非局部区域像素对当前像素分割的指导作用；而在CV值较大的边缘区域，应减小搜索窗及势团参数，以保持图像的几何结构及细节特征。式(10)可以改写为其中ratio是边缘区域的自适应结构指数，可由 CV值决定，CV值越大，细节特征越明显，ratio取值越大。

4 实验分析

4.1实验设置

利用本文提出的自适应贝叶斯分割方法，选用部分 SAR图像进行了分割实验，测试图像均来自Radarsat-1卫星获取的某港口SAR图像(C波段，4视，分辨率10 m)。仿真实验是在Intel(R) Core(TM)i7-2600 CPU @3.40 GHz, 8 GB内存的机器上进行的，编程环境为Matlab 7.10。基于实验运算量等考虑，常用的相似邻域大小为7×7，而非局部搜索窗大小为21×21，本文也采用这种窗口设置。高斯核函数G的标准差取为10, β取为1。实验中，采用传统MRF分割方法、多分辨率MRF(MRMRF)方法[16]和改进方法分别对几幅SAR图像进行分割，优化算法采用收敛速度较快的迭代条件模式(Iterative Condition Model, ICM)。

4.2分割质量评价

图像分割评价可以分为主观评价和客观评价。图3给出了传统MRF方法、MRMRF方法和自适应贝叶斯分割方法的分割结果。将图3(d)与3(b)和3(c), 3(h)与 3(f)和 3(g)对比，可以看出，与传统MRF及MRMRF方法相较，采用改进方法分割结果更为准确，相干斑噪声明显减少，能很好地抑制背景中的强噪声点，并且细节特征明显，局部边缘信息尤其是很弱的边缘信息得到很好的保持，这是因为利用了图像的非局部信息指导当前像素的分割结果；并且采用边缘区域矫正方法对结构保持与过度平滑作适当的权衡。

其中kr为分割k下的比率图像，I为像素强度，m为分类数，n为像素总数，kn为第k类像素总数。

表1给出了3种算法分割效果的对比，可以看出，与传统MRF方法及MRMRF方法相比，本文方法的| |D 与varRI 都变小，这表明后者分割后的区域一致性更好，更为平滑，且对相干斑噪声的抑制作用更有效。

图3 原始图像、传统MRF方法、MRMRF方法和本文方法的比较

表1 3 种算法分割效果对比

5 结论

本文提出了一种融合局部和非局部信息的自适应贝叶斯分割方法，针对SAR图像中的乘性相干斑噪声，引入改进的基于比率概率的相似性测度，用非局部相似像素块指导当前像素的分割；并且考虑分割过度平滑与结构保持的矛盾，采用CV方法获取边缘区域图像模板，对边缘区域进行矫正。在实验分析中，采用改进方法对部分SAR图像进行了分割实验，并与传统 MRF方法进行比较，改进方法的分割结果形状更为准确，不但抑制了相干斑噪声，还有效保持了细节特征，具有显著优势。

[1] 邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1-10.Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J].Journal of Radars, 2012, 1(1): 1-10.

[2] Zhang Peng, Li Ming, Wu Yan, et al.. SAR image multiclass segmentation using a multiscale TMF model in wavelet domain[J]. IEEE Geoscience and Remote Sensing Letters,2012, 9(6): 1099-1103.

[3] 刘国英, 马国锐, 王雷光. 基于 Markov随机场的小波域图像建模及分割Matlab环境[M]. 北京: 科学出版社, 2010:8-14.

[4] Dong Y and Forster B C. Segmentation of radar imagery using Gaussian Markov random field models and wavelet and transform technique[C]. International Geoscience and Remote Sensing Symposium, Singapore, 1997: 2054-2056.

[5] 侯一民, 郭雷. 一种基于马尔可夫随机场的 SAR图像分割新方法[J]. 电子与信息学报, 2007, 29(5): 1069-1072.Hou Yi-min and Guo Lei. A novel SAR image segmentation method based on Markov random field[J]. Journal of Electronics ＆amp; Information Technology, 2007, 29(5):1069-1072.

[6] Zheng Chen, Wang Lei-guang, Chen Rong-yuan, et al.. Image segmentation using multiregion-resolution MRF model[J].IEEE Geoscience and Remote Sensing Letters, 2013, 10(4):816-820.

[7] He Fei-yue, Tian Zheng, Liu Xiang-zeng, et al.. A fast edge tracking algorithm for image segmentation using a simple Markov random field model[C]. International Conference on Computer Science and Electronics Engineering, Hangzhou,2012: 633-636.

[8] Buades A, Coll B, and Morel J M. A non-local algorithm for image denoising[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA,2005: 60-65.

[9] Geman S and Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6): 721-741.

[10] Deledalle C, Denis L, and Tupin F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights[J]. IEEE Transactions on Image Processing, 2009,18(12): 2661-2672.

[11] Coupé P, Hellier P, Kervrann C, et al.. Bayesian non-local means-based speckle filtering[C]. 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro,Paris, 2008: 1291-1294.

[12] Feng Hong-xiao, Hou Biao, and Gong Mao-guo. SAR image despeckling based on local homogeneous-region segmentation by using pixel-relativity measurement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(7): 2724-2737.

[13] 李光廷, 杨亮, 黄平平, 等. SAR 图像相干斑抑制中的像素相关性测量[J]. 雷达学报, 2012, 1(3): 301-308.Li Guang-ting, Yang Liang, Huang Ping-ping, et al.. The pixel-similarity measurement in SAR image despeckling[J].Journal of Radars, 2012, 1(3): 301-308.

[14] Feng Jie, Jiao Li-cheng, Zhang Xiang-rong, et al.. Robust non-local fuzzy c-means algorithm with edge preservation for SAR image segmentation[J]. Signal Processing, 2013, 93(2):487-499.

[15] Otsu N. A threshold selection method from gray-level histogram[J]. IEEE Transactions on System, Man, and Cybernetic, 1979, 9(1): 62-66.

[16] Li Qing-sheng and Liu Guo-ying. Multi-resolution Markov random field model with variable potentials in wavelet domain for texture image segmentation[C]. International Conference on Computer Application and System Modeling,Taiyuan, 2010: 342-346.

[17] Gan L, Wu Y, Liu M, et al.. Triplet Markov fields with edge location for fast unsupervised multi-class segmentation of synthetic aperture radar images[J]. IET Image Processing,2012, 6(7): 831-838.