北斗导航信号BCH译码器中校正子辅助的列表译码算法
2014-11-18朱建锋安建平王爱华
朱建锋安建平 王爱华
(北京理工大学信息与电子学院 北京 100081)
1 引言
2012年 12月,中国北斗卫星导航系统公布了第 1个公开服务信号B1I的接口控制文档(Interface Control Document, ICD),标志北斗卫星导航系统正式提供区域导航定位服务,ICD文件对北斗卫星导航系统的目标和B1I信号结构进行了详细定义[1]。B1I导航信号选择 BCH(15,11)码作为导航电文的纠错码,ICD文件给出了建议的编码、译码实现方法。
卫星导航接收机进行定位解算的前提是获得足够数量的正确的导航电文,因此BCH码译码是影响北斗B1I导航接收机定位成功率和连续性的关键因素之一[2]。BCH码是一种典型的线性分组码,其译码算法已经进行了许多研究,译码算法主要包括:(1)硬判决代数译码,以校正子译码算法为代表[3],该算法复杂度低但编码增益小;(2)软判决最大似然算法及简化,以通用最小距离译码GMD算法[4]、Chase算法[5]、统计排序算法[6]等为代表,编码增益接近最大似然译码,其中Chase算法应用最为广泛,但是 Chase算法中不可靠位搜索和排序运算在FPGA等门电路上串行实现的延时较大[7,8];(3)软判决格形译码,以维特比算法为代表[9,10],在码长较大时具有较好编码增益但是网格数很多。
软判决最大似然算法及其简化算法可以统一到列表译码算法的范畴,即在一个列表或集合上按照某种判决测度搜索最优的译码结果,列表译码算法性能决定于译码列表的构造和搜索算法的效率,Chase算法是通过不可靠位的排序建立较小的译码列表从而获得效率改善。校正子辅助的列表译码算法以相同的校正子和汉明重量为准则构造多个错误模式列表,根据接收数据硬判决序列的校正子选择错误模式列表,使用相关函数差作为判决测度搜索最优错误模式并译码。
2 校正子辅助的列表译码算法
2.1 算法原理
北斗系统 B1I导航信号中使用的 BCH(15,11)码生成多项式为,最小汉明距,可以纠正所有1 bit错误,非0的校正子共有15种情况。校正子辅助的列表译码算法原理如图1所示。

图1 校正子辅助的列表译码原理
译码过程包括3个基本步骤:数据预处理、选择错误模式列表和最优错误模式搜索,数据预处理将接收数据进行硬判决并计算校正子和取绝对值产生置信度序列,根据硬判决序列的校正子选择15个错误模式列表中的1个,按照判决测度搜索最优错误模式并完成译码。更大错误模式列表可以以更大的概率搜索到正确错误模式,但是列表元素数的增加需要更多时间计算判决测度和搜索最优错误模式,采用何种判决测度则决定了单个列表元素的计算复杂度,因此,错误模式列表和判决测度构造是优化列表译码算法的关键。
2.2 错误模式列表构造
列表译码算法中列表的构造包含两项内容:元素内容和元素数量,在最大似然译码中,列表中的元素是所有可能的码字,在Chase算法中通过搜索P个不可靠位置确定列表中的元素是2P个试探码字,列表构造需要在列表覆盖能力和规模之间进行折中。对于(N,K)线性分组码,接收码字R C E= + ,校正子S满足:

其中C为正确码字,E为错误模式,式(1)表明校正子S只和错误模式E有关,与码字C无关。错误模式E是一个N维的线性空间,通过校验矩阵H的映射生成一个(N K- )维的线性空间,错误模式 E和校正子S之间为多对一的映射关系,分组码译码可以转化为在N维线性空间上对最佳错误模式E的搜索问题[11,12]。校正子辅助列表译码算法以错误模式作为列表元素,通过搜索最佳错误模式进行BCH(15,11)码的译码,错误模式列表的构造依照两个准则:汉明重量和校正子。
在典型的AWGN信道下,码字中错误的个数符合二项式分布,N bit的码字发生i个错误的概率为

其中p为比特误码率。式(2)表明:当 1Np< 时,码字错误概率随着错误比特数增加而降低,大部分错误码字中错误数都在一个特定门限之下。采用实验仿真的方法分析错误模式的分布规律,以 BCH(15,11)码为编码方案,在 AWGN 信道下统计错误模式分布,信噪比范围从 1~8 dB,每个信噪比点生成100000个码字,分别统计汉明码重W为0,1,2,3和3以上的错误模式个数,其中 0W= 代表码字没有发生错误。
表1中的数据表明:随着信噪比的增加,BCH(15,11)码的错误模式主要是两种情况,以作为选择错误模式的门限建立列表可以以很大的概率覆盖错误模式。对于码的错误模式有15种,的错误模式有种,错误模式列表中元素总数为120个。
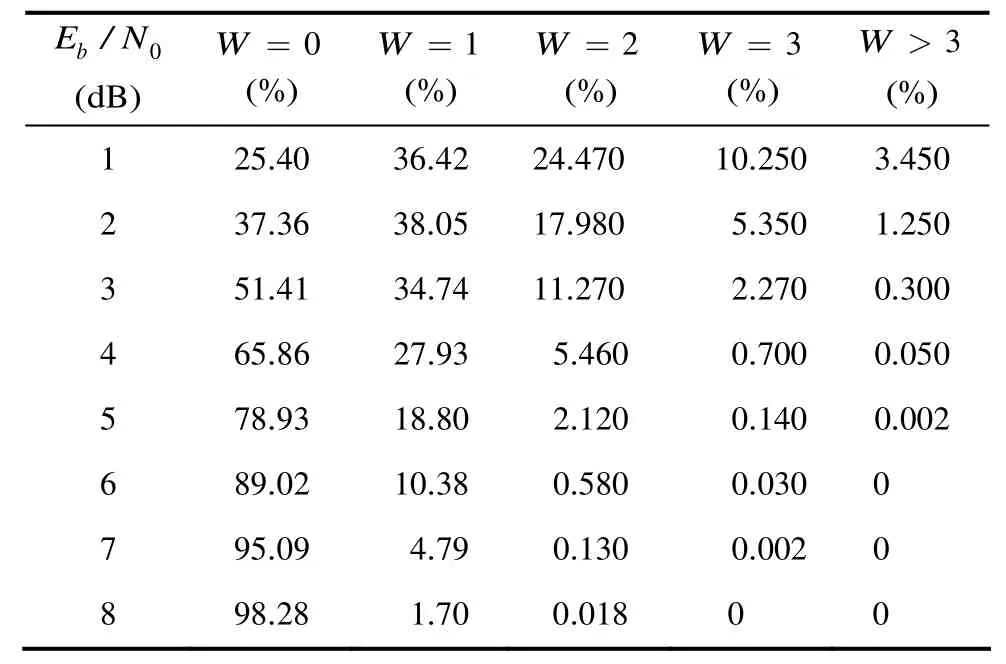
表1 不同信噪比下BCH(15,11)的错误模式分布
对于(N,K)线性分组码,校正子和错误模式之间存在线性映射关系,因此利用校正子对错误模式列表进行进一步的分割。由于从错误模式到校正子是一个从N维到N K- 维的映射,因此存在多个错误模式对应一个校正子的情况,要利用校正子分割错误模式列表需要解决一个错误模式对应于多个校正子的问题,即证明不同的校正子对应不同的错误模式,证明过程如下。
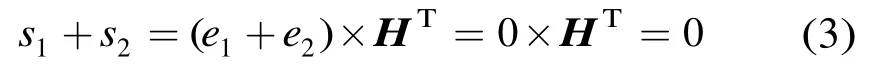
与假设相矛盾。所以

证毕
性质1表明,不同的错误模式可能具有相同的校正子,但是不同的校正子一定对应不同的错误模式。
利用性质1的结论将120个 2W ≤ 的错误模式细分到15个列表,同一列表中的错误模式具有相同的校正子,平均每个列表中有8个元素。
2.3 相关函数差判决测度
欧氏距离是软判决译码最常用的判决测度,码字C和接收序列R的欧氏距离定义为

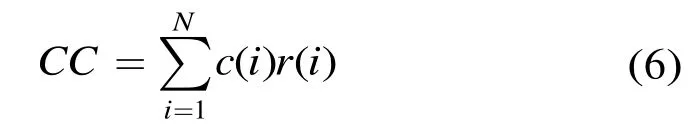
对于 BCH软判决译码,首先计算接收序列 R的置信度序列α和硬判决序列β。

则有

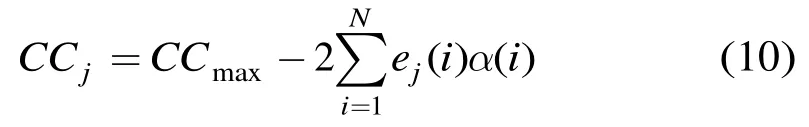
定义相关函数差:
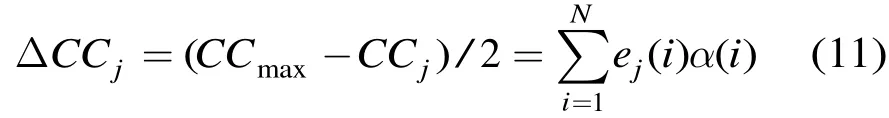
式(11)表明最大相关函数准则等价于最小相关函数差,当错误模式E的码重时,的计算只需要1次加法即可完成。
综合上述分析,最小欧氏距离准则、最大相关函数准则、最小相关函数差准则在BCH译码中是等价的,3种不同判决测度的计算复杂度比较如表 2所示,最小相关变化量具有最小的计算复杂度。
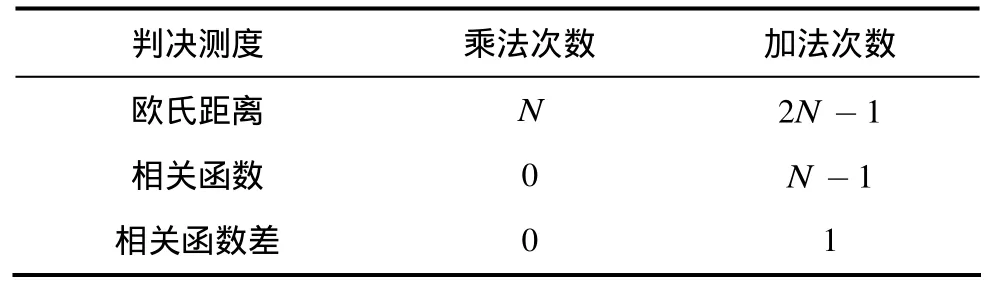
表2 不同判决测度的计算复杂度
3 北斗B1I导航信号BCH译码实现与性能仿真
3.1 校正子辅助的列表译码器实现
综合错误模式列表的构造和判决测度优化改进,北斗系统B1I导航信号BCH码的译码步骤如下:
步骤2 数据初始化。按照式(7)和式(8)处理接收序列r生成硬判决译码序列β和置信度序列α;
步骤3 选择错误模式列表。计算硬判决序列β的校正子 s,如果 0s= 将转入步骤 6,否则按照 s选择相应的校正子模式列表E;
步骤 5 搜索最优错误模式。按照最小相关函数差准则搜索最优错误模式 e,译码序列为;
步骤 6 译码输出。抽取译码序列的前 11 bit作为译码结果输出。
基于校正子估计的译码计算复杂度主要在步骤3中的1次校正子计算和步骤4中的EN 次判决测度计算,这两个步骤都是线性复杂度,EN 个判决测度计算在FPGA和DSP中可并行实现以进一步改善译码延时。
3.2 性能仿真与分析
编码理论表明纠错编码存在性能界,与性能界的差距是衡量译码算法优劣的主要依据。联合界是AWGN信道下线性分组码可实现的性能界[14],对于线性码其误码率的上界为

为验证软判决译码算法的性能和计算复杂度,在AWGN信道下对北斗B1I信号BCH码进行最大似然算法,Chase算法和校正子辅助列表译码算法进行了仿真实现。仿真的条件:AWGN信道,BPSK调制,信噪比步进0.01 dB,误码率,仿真实验要求至少100个错误码字以保证置信度,Chase算法不可靠位数 3P= 。不同译码算法的BCH(15,11)
码性能如图2所示。
最大似然算法,Chase算法和校正子辅助算法的译码复杂度比较如表3,校正子辅助算法的复杂度远小于另外两种算法。

图2 BCH(15,11)码不同译码算法性能比较

表3 BCH(15,11)码不同译码算法的复杂度比较
4 结论
北斗B1I信号是北斗系统的第1个公开服务信号,其目标是面向广大民用市场提供普遍服务,B1I信号BCH译码算法研究在研制面向区域服务的北斗导航接收机中具有重要作用[15]。校正子辅助的列表译码算法在误码率 10-5时,与最大似然译码的信噪比仅差0.08 dB,性能非常接近最大似然译码算法和Chase译码算法,是一种近优的软判决译码算法。新算法具有计算复杂度低、不要排序运算和可并行优化等特点,适合工程化实现和应用。
[1] China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B1I (Version 1.0)[S]. 2012.
[2] 陈金平, 王梦丽, 钱曙光. 现代化GNSS导航电文设计分析[J].电子与信息学报, 2011, 33(1): 211-217.
[3] 连帅, 闫利军, 孙科. 北斗2代卫星导航电文纠错校验设计与仿真[J]. 计算机测量与控制, 2010, 18(10): 2344-2347.
[4] Forney G Jr. Generalized minimum distance decoding[J].IEEE Transactions on Information Theory, 1966, 12(1):125-131.
[5] Chase D. Class of algorithms for decoding block codes with channel measurement information[J]. IEEE Transactions on Information Theory, 1972, 18(1): 170-179.
[6] Fossorier M P C and Shu Lin. Soft-decision decoding of linear block bodes based on ordered statistics[J]. IEEE Transactions on Information Theory, 1995, 41(5): 1379-1396.
[7] Skliarova I, Sklyarov V, Mihhailov D, et al.. Implementation of sorting algorithms in reconfigurable hardware[C]. 2012 16th IEEE Mediterranean Electro technical Conference(MELECON), Yasmine Hammamet, Tunisia, 2012: 107-110.
[8] García-Herrero F, Canet M J, Valls J, et al.. High-throughput interpolator architecture for low-complexity chase decoding of RS codes[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2012, 20(3): 568-573.
[9] Honary B and Markarian G. Low-complexity trellis decoding of hamming codes[J]. Electronics Letters, 1993, 29(12):1114-1116.
[10] Michelson A M and Freeman D F. Viterbi decoding of the (63,57) Hamming codeimplementation and performance results [J]. IEEE Transactions on Communications, 1995,43(11): 2653-2656.
[11] Snyders J. On survivor error patterns for maximum likelihood soft decoding[C]. 1991 IEEE International Symposium on Information Theory, Budapest, Hungary, 1991:192.
[12] Snyders J. Reduced lists of error patterns for maximum likelihood soft decoding[J]. IEEE Transactions on Information Theory, 1991, 37(4): 1194-1200.
[13] 朱建锋, 安建平, 王爱华. 导航电文BCH(15,11)编码的低复杂度软判决译码[C]. 第4届中国卫星导航学术年会(CSNC 2013), 武汉, 2013-05-15.
[14] Fossorier M P C, Shu Lin, and Rhee D. Bit-error probability for maximum-likelihood decoding of linear block codes and related soft-decision decoding methods[J]. IEEE Transactions on Information Theory, 1998, 44(7): 3083-3090.
[15] Montenbruck O, Hauschild A, Steigenberger P, et al.. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system[J]. GPS Solutions, 2013, 17(2): 211-222.
