认知无线电中的稀疏信道估计与导频优化

戚晨皓吴乐南 朱鹏程

(东南大学信息科学与工程学院 南京 210096)

1 引言

智能手机的迅速普及和通信技术的快速发展对频谱提出了更高的需求，频谱资源短缺的现象日益明显。而另一方面，已获得授权的频段没有得到充分利用，大量频段处于闲置或很少使用的状态[1]；由此，产生了认知无线电(Cognitive Radio, CR)技术。利用该技术，在保障主用户(Primary Users, PUs)优先使用其频段的前提下，从用户(Secondary Users,SUs)也可使用这些频段；因此，该技术有望在不开辟新频段的情况下，大幅提高现有频段的频谱利用率。

正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)作为当前移动通信及未来无线通信的核心技术，能有效对抗无线传播中的多径效应，简化均衡器设计，降低接收机复杂度和功耗，并提高频谱利用率。OFDM利用多个子载波并行传输数据，能灵活地填充频谱空穴；那些与PUs发生频段冲突的OFDM子载波可随时停用，而剩下的子载波则继续用于SUs的数据传输，因此，OFDM是一项适用于认知无线电的重要技术[2]。

OFDM 信道估计对信号传输所经历的信道的时延、衰减、多径等参数进行估测，信道估计的准确程度对信道均衡、解调和信道译码等均有直接影响。因此，信道估计技术是OFDM系统的关键环节之一。最近新出现的稀疏信道估计(Sparse Channel Estimation)[3]也称为压缩信道感知(Compressed Channel Sensing)[4]，利用无线信道的稀疏性，将压缩感知(Compressed Sensing, CS)技术用于信道估计。相比传统的最小二乘(Least Squares, LS)或最小均方误差(Minimum Mean Square Error, MMSE)信道估计，稀疏信道估计能大幅度降低导频开销，提高频谱利用率和信道估计精度。考虑到无线信道的时延扩展和接收机前端较高的采样率，信道多径分量分散于这一时延扩展中，经过采样以后的信道冲击响应(Channel Impulse Response, CIR)序列通常呈现大多数为零，仅少数非零的稀疏性，尤其对于普遍使用过采样技术的OFDM系统，这一稀疏特性更为明显[5]。目前，正交匹配追踪(Orthogonal Matching Pursuit, OMP)，压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)，基追踪(Basis Pursuit, BP)，迭代支集检测(Iterative Support Detection, ISD)等算法已被用于 OFDM 稀疏信道估计[6]，并获得了比 LS和MMSE更好的信道估计性能。

然而，基于稀疏信道估计的OFDM导频设计，目前仍然是一个开放性的课题。在采用稀疏信道估计的OFDM-CR系统中，一旦与PUs发生频段冲突就会导致一些OFDM子载波停用，SUs如何从剩下的可用子载波中选择一组最优的子载波，使稀疏信道估计性能最优，值得我们深入研究。文献[7]基于LS信道估计研究了OFDM-CR系统中的导频设计，以最小化信道估计均方误差(Mean Square Errors, MSE)的上界为目标函数进行优化，并将其进一步分解为一系列1维的低复杂度子问题求解。文献[8]采用凸优化和叉熵优化进行 OFDM-CR 系统导频设计，但仍旧基于传统的LS信道估计。文献[9]研究了非连续正交频分复用(Non-Continuous OFDM, NC-OFDM) CR系统中基于压缩感知的信道估计方法，以“最小化测量矩阵的互相关”作为优化目标，对导频进行优化，提出了采用随机搜索获取最优导频的方法。

本文首先将OFDM-CR系统的信道估计转化为一个稀疏重建问题，考虑以最小化观测矩阵的互相关为目标进行优化；其次，根据系统参数预生成一个2维表，将导频优化问题转化为表的列选取问题，采用查表方式快速计算任一导频序列的目标函数；在此基础上，提出了一种快速的导频优化算法，通过灵活设置外循环和内循环次数，对导频序列进行逐位置替换与优化。

2 系统模型

本文所研究的OFDM-CR系统如图1所示，其最大的特点在于，采用稀疏信道估计代替了传统的LS或者MMSE信道估计，充分发掘了无线信道的稀疏性。由于稀疏信道估计基于压缩感知理论，采用对无线信道进行稀疏重建的思想，与LS和MMSE信道估计本质上完全不同，因此，在后者中被证明为最优的等间隔导频排布[10]是否依然适用于前者，值得深入研究。图1所示系统，首先根据频谱感知获得可用的子载波集合，随后进行导频优化，选择一组最优的子载波用于传输导频，其余子载波可用于传输数据，最后将导频优化结果通过控制信道广播给接收机。

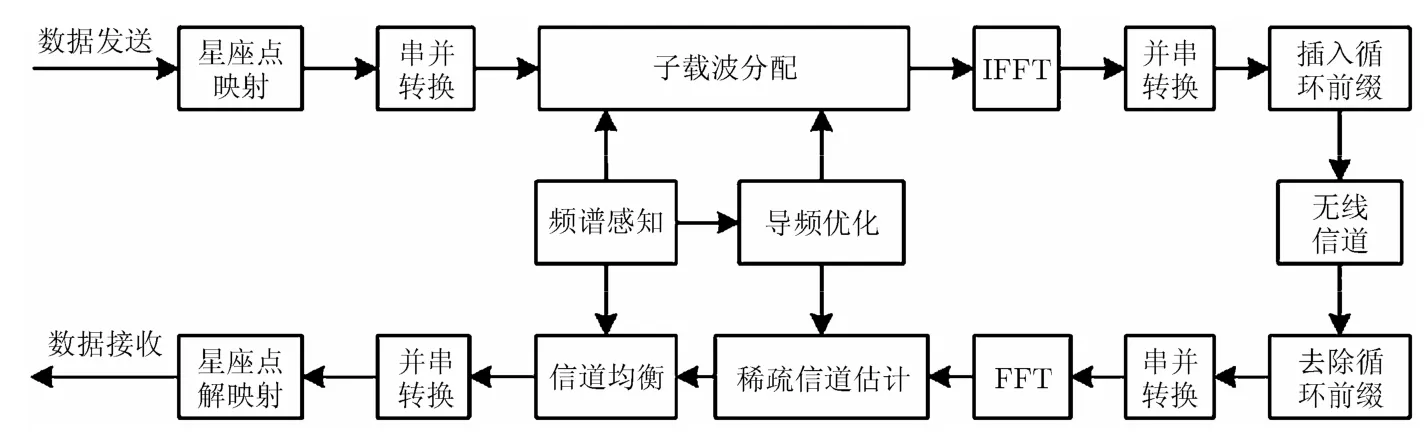
图1 采用稀疏信道估计的OFDM-CR系统框图

σ的复高斯分布。

则式(2)可写为

若K＆gt;L且A列满秩，可获得h的LS估计为

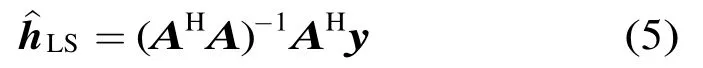
其中，上标“H”表示向量共轭转置。然而，若能降低导频开销，使K＆lt;L，可进一步提高频谱效率和数据传输速率。根据文献[4-6]可知，h是稀疏的，即h的L个元素中，大多数为零，而仅有少数非零。因此，稀疏信道估计本质上是在噪声项w未知的情况下，由已知的y和A来估计h，并充分利用h稀疏这一先验信息。为提高稀疏重建的稳定性和可靠性，Candes和Tao等[11]指出，若A满足有限等距性质(Restrict Isometry Property, RIP)，在无噪声的情况下，利用y和A能以很高的概率重建h，这类矩阵包括高斯矩阵，Toeplitz矩阵[12]等。然而，任意给定一个矩阵A，很难检验其是否满足RIP条件。一种相对便捷的途径是研究A的互相关，A的互相关越低，稀疏重建的概率越高[13,14]。

定义矩阵A的互相关为

其中Am表示A的第m列。将式(3)代入式(6)，得到

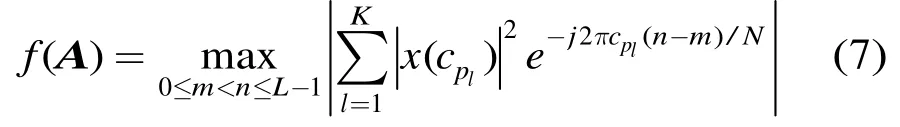
假设发送的导频功率相同，即

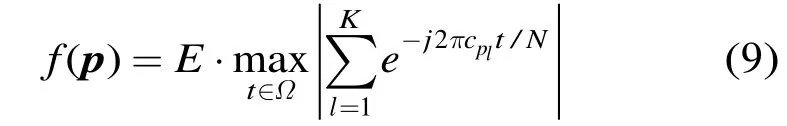
其中，用p代替A作为自变量，是由于在导频功率相同，L给定的情况下A和p能相互唯一确定。因此，该OFDM-CR系统的导频优化问题本质上是求解式(9)的最小化问题。

而最优的导频序列为

由于式(8)中E的大小对求解optp 并没有影响，此处不妨假设 1E= 。

为求解式(10)，生成一个 1L- 行，M列的表，如式(12)：对于任意给定的一个导频序列p，根据式(9)，首先从T中找出列号为p的K个列，构成一个 1L- 行，K列的子矩阵︿T；由于通过索引号可快速访问T的各列，因此该过程实现起来十分迅速。然后对︿T的每行求和，构成一个 1L- 维的列向量，选取该列向量中绝对值最大的元素，即为 ()f p。由于T可预先生成，采用查表可快速计算得到 ()f p。因此，直观上可以通过穷举所有可能的p并计算相应的目标函数 ()f p，从中选取对应于最小目标函数值的导频序列作为最优导频序列。然而，当M和K较大时，穷举将十分困难，例如，，不同的导频序列将高达261.3710×个，计算每个导频序列对应的目标函数不切实际，因此，本文将在下一节提出一种高效的导频优化算法。

3 导频优化算法

本文提出了一种高效的导频优化算法，主要包括“初始化”、“迭代循环”和“结果输出”，在“迭代循环”中，算法采用两层嵌套循环外循环和内循环，对导频序列进行逐位置优化。

步骤 1 初始化：算法共有两层嵌套循环，设外循环次数为U、内循环次数为I。设Z为一个U行，K列的全零矩阵，Z的每一行用于存放一种导频序列，Z中一共存放U种导频序列。设v为一个U行的零向量，用于存放Z中U种导频序列对应的目标函数值。

步骤2 循环迭代：

(1)外循环：对于每一次外循环l=1,2,…,U，从频谱感知获得的当前可用子载波构成的集合 =c中随机选出K个元素，构成一个导频序列p。设为一个长度为K的零向量，用于存放上一次内循环的导频优化结果。运行步骤(2)内循环。将p保存于Z的第l行，将p对应的目标函数()f p保存于v的第l个元素。

(2)内循环：对于每一次内循环n=1,2,…,I，若p与︿p相同，表示本次内循环的优化结果与上一次内循环的优化结果完全相同，因此没有必要继续运行下去，跳出内循环；若p与不同，运行步骤(3)逐位置优化。将p的每一个元素赋值给，使p与两者完全相同。

(3)逐位置优化：对于p的每一个位置 m=1,2,…,K，固定p的所有K个元素中除第m个元素之外的其余K-1个元素，在p的第m个元素位置上选取候选集中的最佳元素。具体来说，对于导频排布，首先固定p的所有K个元素中除第m个元素外的其余K-1个元素，即固定和不变，其次设集合Φ为p中除第m个元素外的其余K-1个元素构成的集合，即，设候选集Λ为c与Φ的差集，即，每次从集合Λ中取出一个不同的元素，放到p的第m个元素位置上，一共有M-K+1种放法；对于每一种放法形成的导频序列 *p，均可计算其目标函数 *()fp ；从这M-K+1个目标函数中选取最小的一个，假设作为第m个元素位置上最佳的目标函数值，并将其对应的导频序列作为第m个元素位置对应的最佳导频序列。

从p的所有K个位置对应的K个最佳导频序列中，选取目标函数值最小的导频序列，假设，将赋值给p。

步骤3 结果输出：从v的所有U个元素中选出一个最小的(若同时有多个最小的，任选一个)，假设v的第i个元素取到最小值，输出矩阵Z的第i行，即为导频优化结果。

4 仿真结果分析

对一OFDM-CR系统，子载波数目N=1024，划分为64个子带，每个子带包含16个OFDM子载波。假设SUs通过频谱感知获知频段中部的32个子带，共计512个子载波已被PUs使用，即SUs当前可用32个子带共计M=512个OFDM子载波，构成的可用子载波集合为，从中选取K=16个导频子载波，用于导频辅助稀疏信道估计。稀疏重建采用主流的OMP算法，它在重建性能和复杂度之间具有合理的折中，在目前实际应用中最为广泛。假设信道总抽头数目L=50，其中仅有S=4个非零抽头。在每一次信道的具体实现中，从L个抽头中任选S个抽头作为非零抽头，非零抽头系数满足均值为 0，方差为1的复高斯分布[15]。OFDM保护间隔为256，采用QPSK调制，并采用低复杂度的单抽头迫零均衡进行频域信道均衡。

根据式(12)，首先生成一个49行，512列的表T，对于给定的一个导频序列p，根据索引号从T中可快速找出对应的16个列，构成一个49行，16列的子矩阵；然后对的每行求和，构成一个49行的列向量，选取该列向量中绝对值最大的元素即为。若通过穷举所有可能的p并计算相应的目标函数 ()fp，搜索空间高达298.410×，计算每个导频序列对应的目标函数并从中选取最小的导频序列，如此巨大的运算量几乎无法实现。为此，文献[9]提出了一种随机搜索算法，每次随机生成一个导频序列并计算其目标函数值，在给定的时间内，重复该步骤，用这段时间内最小目标函数对应的导频序列作为最优导频序列。图2给出了本文所提出的算法与文献[9]算法的收敛性能对比。仿真平台基于Windows 7操作系统，MATLAB 2011a软件，CPU为双核2.5 GHz，内存3 GByte。对于本文提出的算法，设定外循环次数U=2000，内循环次数I=15，算法运行34 s后获得一个优化的导频序列及相应的目标函数值 6.3938。而采用该随机搜索算法，设定相同的运行时间 34 s(即相同的计算复杂度)，运行后得到的一个优化导频序列及相应的目标函数值6.8576。如图 2所示，本文所提出算法的收敛速度明显快于文献[9]提出的算法，能获得更小的目标函数及更优的导频序列；同时也说明，要实现相同的目标函数值，本文算法所需的运行时间远少于文献[9]算法，从而反映出本文算法具有更低的计算复杂度。因此，这对实际OFDM-CR系统中SUs从当前可用的子载波中快速找出一组优化的导频，意义十分重大。

考虑到 MMSE信道估计通常需要信道的二阶统计信息，比如信道的协方差矩阵等，而本文采用的稀疏信道估计不需要二阶统计信息，因此，将本文算法与同样不需要二阶统计信息的 LS信道估计进行对比。图3和图4分别给出了OFDM-CR系统采用稀疏信道估计和 LS信道估计的均方误差(Mean Square Errors, MSE)和误码率(Bit Error Rate, BER)性能对比。由于等间隔排布的导频序列已被证明为LS信道估计的最优导频排布[10]，因此，分别采用了导频间隔为9和10的等间隔导频序列进行 LS信道估计，并分别采用文献[9]算法优化的导频序列和本文算法优化的导频序列进行 OMP稀疏信道估计。考虑到一般BER低于时，信道编码能基本消除误码，仿真时信噪比上限设置为20 dB。如图4所示，采用本文算法优化导频的OMP信道估计，性能略优于采用导频间隔为9的LS信道估计，前者的导频数目为16，而后者的导频数目为58，因此，前者相比后者能节省 72.4%的导频开销，能提高8.2%的频谱利用率。此外，本文算法性能优于文献[9]算法，为达到相同的 0.012的误码率，前者相比后者能节省约5 dB的信噪比。

5 结束语

本文研究了采用稀疏信道估计的认知无线电系统及导频优化，将信道估计转化为稀疏重建问题，考虑以最小化观测矩阵的互相关为目标进行优化；根据系统参数预生成一个2维表，将导频优化问题转化为表的列选取问题，采用查表方式快速计算任一导频序列的目标函数；在此基础上，提出了一种快速的导频优化算法，通过灵活设置外循环和内循环次数，对导频序列进行逐位置替换与优化。仿真结果验证了本文工作的有效性，相比于最小二乘信道估计，稀疏信道估计能节省了72.4%的导频开销，提高了8.2%的频谱利用率；此外，本文提出的导频优化算法优于目前的随机优化算法，在相同的0.012误码率性能下，前者相比后者能节省约5 dB的信噪比。

图2 两种算法的收敛性能对比

图3 采用稀疏信道估计和LS信道估计的MSE性能对比

图4 采用稀疏信道估计和LS 信道估计的BER性能对比

[1] Tandur D, Duplicy J, Arshad K, et al.. Cognitive radio systems evaluation: measurement, modeling, and emulation approach[J]. IEEE Vehicular Technology Magazine, 2012,7(2): 77-84.

[2] Zhou X, Li G, and Sun G. Multiuser spectral precoding for OFDM-based cognitive radio systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(3): 345-352.

[3] Bajwa W, Haupt J, Sayeed A, et al.. Compressed channel sensing: a new approach to estimating sparse multipath channels[J]. Proceedings of the IEEE, 2010, 98(6): 1058-1076.

[4] Berger C, Wang Z, Huang J, et al.. Application of compressive sensing to sparse channel estimation [J]. IEEE Communications Magazine, 2010, 48(11): 164-174.

[5] Qi C and Wu L. Application of compressed sensing to DRM channel estimation[C]. IEEE 73rd Vehicular Technology Conference (VTC-Spring 2011), Budapest, Hungary, 2011:1-5.

[6] Meng J, Yin W, Li Y, et al.. Compressive sensing based high-resolution channel estimation for OFDM system [J].IEEE Journal on Selected Topics in Signal Processing, 2012,6(1): 15-25.

[7] Hu D, He L, and Wang X. An efficient pilot design method for OFDM-based cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 10(4):1252-1259.

[8] Manasseh E, Ohno S, and Nakamoto M. Pilot design for noncontiguous spectrum usage in OFDM-based cognitive radio networks[C]. European Signal Processing Conference(EUSIPCO), Bucharest, Romania, 2012: 465-469.

[9] 何雪云, 宋荣方, 周克琴. 认知无线电NC-OFDM系统中基于压缩感知的信道估计新方法[J]. 通信学报, 2011, 32(11):85-94.He X Y, Song R F, and Zhou K Q. Compressive sensing based channel estimation for NC-OFDM systems in cognitive radio context[J]. Journal on Communications, 2011, 32(11): 85-94.[10] Tong L, Sadler B, and Dong M. Pilot-assisted wireless transmissions: general model, design criteria, and signal processing[J]. IEEE Signal Processing Magzaine, 2004, 21(6):12-25.

[11] Candes E J and Tao T. Decoding by linear programming[J].IEEE Transactions on Information Theory, 2005, 51(12):4203-4215.

[12] Haupt J, Bajwa W, Raz G, et al.. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]. IEEE Transactions on Information Theory,2010, 56(11): 5862-5875.

[13] Qi C and Wu L. A study of deterministic pilot allocation for sparse channel estimation in OFDM systems[J]. IEEE Communications Letters, 2012, 16(5): 742-744.

[14] Qi C and Wu L. Tree-based backward pilot generation for sparse channel estimation[J]. Electronics Letters, 2012, 48(9):501-503.

[15] Qi C and Wu L. Optimized pilot placement for sparse channel estimation in OFDM systems[J]. IEEE Signal Processing Letters, 2011, 18(12): 749-752.