高斯Wiretap模型下基于部分陪集的无线物理层强安全编码
2014-11-18鸣季新生黄开枝郭淑明
易 鸣季新生 黄开枝 钟 州 郭淑明
(国家数字交换系统工程技术研究中心 郑州 450002)
1 引言
无线物理层安全编码是一种在保证授权双方信息传输可靠性的基础上,进一步考虑信息传输安全性的信道编码技术。其目的是使授权双方的私密信息能够正常传输,而使窃听方无法获得任何私密信息。其优点是不需要通信双方事先分配或协商密钥加密,在物理底层直接防止第3方窃听。
1975年Wyner[1]针对有线通信网络首次提出了基于信息理论安全的Wiretap模型,证明了当合法信道质量优于窃听信道时存在安全容量,文献[2]进一步将该模型拓展到广播信道,并利用典型序列理论,证明了在该模型下逼近安全容量的码字是存在的。文献[3]首次给出了一种合法信道无噪,窃听信道为二进制纯擦除信道(Binary Eraser Channel,BEC)Wiretap模型下的具体物理层安全编码方式——陪集编码。合法信道无噪使得安全编码不需要考虑纠错性能,只需要重点关注安全性。有线通信网络中物理层的信息传输错误率较低,通过校验、重传等机制可以实现合法信道无噪,然而无线信道必定有噪,尽管可以利用功率控制等技术实现合法信道的近似无噪,但这种方法能效比很差。针对无线通信中合法信道噪声不易消除的问题所设计的安全编码,需要既能保证安全又要有一定的纠错能力。文献[4]将陪集编码和纠错码级联,具有较好的纠错能力,但安全性能很差,例如码字中存在某个比特为奇偶校验,一旦该比特泄露给窃听者,窃听者就获得了一半的信息。为了保证信息传输过程中的强安全性,文献[5]和文献[6]将陪集的概念扩展到格码,研究了合法信道为高斯和瑞利信道下的安全编码,但此类方法在维数较高时实现复杂度非常大。文献[7]以低密度奇偶校验码为基础进行陪集编码,并从降低复杂度的角度进行了深入讨论,但该方法要求合法信道无噪,实用性不强。文献[8-10]以具有良好纠错性能的码为母码,在此基础上不传私密信息或者加入随机冗余来增加私密信息的不确定度,然后利用合法及窃听信道质量差异和母码良好的纠错性能,实现合法信道上私密信息的正确恢复,而窃听信道无法获得私密信息;文献[11]和文献[12]证明了此类编码本质上是属于窃听信道容量可达码,不能保证信息的强安全传输,且安全级别不高。针对多天线系统,文献[13]提出了一种基于信道特征随机投影的物理层安全编码方式,文献[14]提出了一种分布式天线跳空收发技术,它们都是通过增加一个随机变化的预编码矩阵实现合法者正确接收,而窃听者无法收到任何信息,但合法通信双方都需要精确知道每个传输时刻的信道状态信息。文献[15]首先利用合法通信双方的交替反馈和低密度奇偶校验码的纠错能力,使合法信道转化为基本无噪,窃听信道仍然保持较高误比特率,然后利用陪集编码实现安全传输,随着合法信道质量变差,其信息交互量也随之增大。
为了保证编码强安全性的同时提高其在合法信道的抗噪性能,本文在二元域上,针对合法信道为高斯噪声信道,窃听信道为 BEC信道的 Wiretap模型,提出一种基于部分陪集的强安全编码方法。为了保证编码方法的强安全性,本文证明了部分陪集强安全编码的充分必要条件:当且仅当陪集母码的对偶码的最小码字距离大于信息泄露位数时,利用部分陪集编码可以保证私密信息的强安全传输。为了提高部分陪集编码的可靠性和有效性,本文在全体陪集集合中尽量多地选取陪集间最小汉明距离尽量大的陪集作为可用陪集进行安全编码,并利用部分陪集间的汉明距离提高码字的抗噪声性能。为解决该问题,首先需要计算两两陪集间的最小汉明距离,本文通过深入分析陪集编码的性质,当陪集母码为时,将其计算量从次异或运算降低为1次查表运算,同时将陪集编码器的内存需求从2nnbit减少为2knbit;然后将问题等效为搜索无向图的最大完全子图问题,并设计了基于树形深度优先的搜索算法,得到了给定距离冗余下势最大的部分陪集集合。
2 无线物理层安全编码模型与相关定义
总结现有Wiretap模型,无线物理层安全编码的基本模型如图1所示。图1中所示的合法信道和窃听信道均是易受干扰的无线信道。

图1 无线物理层安全编码模型

陪集的最小汉明重量是陪集中所有元素的最小汉明重量。
3 基于部分陪集的强安全编码方法
现有的强安全编码方案抗干扰性差,不适用于无线通信系统,而合法信道有噪情形下的物理层安全编码又不能满足信息传输的强安全性要求,为此本文提出了基于部分陪集的强安全编码方法。该方法的基本思想是利用陪集内的随机冗余保证强安全性,利用陪集间的距离冗余保证可靠性,通过寻找给定距离冗余下势最大的可用陪集集合保证编码的有效性。该方法首先根据系统的安全性要求选择合适的陪集母码,得到能够保证强安全性的全体陪集集合,然后计算所有陪集间最小汉明距离,再搜索给定陪集间最小汉明距离下势最大的部分陪集集合,最后利用所得的部分陪集进行编码映射。具体编码步骤如下:
步骤 1 根据系统安全性要求,选择合适母码进行陪集划分。假设系统强安全性所允许的最高信息泄露比例为λ,当且仅当码的对偶码的最小码字距离时,由步骤4的陪集映射能够保证信息传输的强安全性,本文第3.1节将对该方法的强安全性进行证明;
步骤 4 陪集映射。将每个待传的私密消息pM映射到一个陪集整体pCO,编码时随机选择陪集中的任何一个元素作为实际传送的码字X,当每个陪集中都至少有一个元素与窃听者所得到的码字一致时,窃听者无法区分所接收到的码字属于哪个陪集,即没有获得任何关于私密消息的信息。传统信道编码将信息映射到码字,即从一个包含2k元素的空间mS 映射到一个包含2n个元素的空间cS,但是仅选取了cS中的部分元素作为可用码字,剩余的码字作为禁用码字不发挥任何作用。为此,我们在整个cS空间内重新考虑,将编码的研究对象从传统的码字扩展为“码字云”,即一组码字的集合(陪集),由于实际传送的码字X是随机选取的,本质上是利用陪集内部的随机冗余保证私密信息的安全传输。
3.1 部分陪集编码的强安全性证明
为了说明部分陪集编码可以保证私密信息的强安全传输,本节给出定理1。
所以,(1)当且仅当生成矩阵中泄露位相对应列构成的子矩阵中各列线性无关时,对任意iCO,存在相应的s位,即每个陪集中都至少存在一个元素去除擦除符号后与一致。(2)当且仅当的最小距离时,每个陪集中至少存在一个元素去除擦除符号后与sZ一致,使得式(2)成立:

式(2)成立即满足式(1)所描述的强安全性。定理1是构造强安全性陪集的基础。显然当陪集集合SC满足定理1时,从其中选取的部分陪集也能保证信息传输的强安全性。
证毕
3.2 计算陪集间最小汉明距离方法的可行性证明
陪集间的最小汉明距离决定编码的抗噪声性能。为了得到给定距离冗余下势最大的可用陪集集合,首先需要计算任意陪集间的最小汉明距离。为了减少其计算量,本节给出定理2至定理5。
证明 因为同一陪集中不同元素的伴随式是相同的,不同陪集的伴随式不同,令pS表示第p个陪集的伴随式,它是一个k维的向量,取值从全0到全1。假设C的校验矩阵经过初等行变换为 =H为单位阵。所以,存在,使得式(3)成立:
因为pS 的取值从全0到全1只有中可能,且为单位矩阵,所以,每个陪集中有且只有一个前bit为0的元素,且该元素的后kbit从全0到全1,即各陪集中有且仅有一个元素是矩阵A中的行矢量:
证毕
定理 3 线性陪集安全编码的性能是由码字C唯一确定。
证明 由于陪集中的任意元素都可以作为该陪集的首,即矩阵A中的行矢量可以作为相应陪集的首元素,则当码字C确定后,关于该码字的陪集划分也随之确定,不同陪集首对应的只有陪集内的元素顺序和陪集间次序的不同,不影响陪集间距离的计算,即线性陪集安全编码的性能由码字C唯一确定。
证毕

证毕
定理 5 任意两个不同陪集间元素的异或一定构成另一陪集。
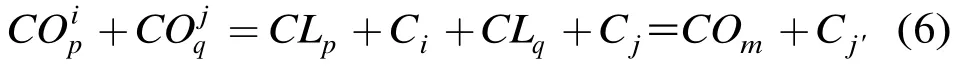
因为陪集中的任意元素都可以作为陪集首,所以,任意两个不同陪集间元素的异或一定构成另一陪集。 证毕
推论 1 任意两个不同陪集间的最小距离一定是另一个陪集的最小汉明重量。
证明 结合定理4,由陪集间最小距离和陪集最小汉明重量的定义可得。
证毕
3.3 基于树形深度优先搜索的部分陪集计算算法
证毕
求一个无向图的最大完全子图是图论中的经典问题,相应地有各种确定性或启发式求解算法,为了获得全局最优解,本文提出一种基于树形深度优先的搜索算法。算法步骤见表1。

表1 树形深度优先搜索算法
算法示例如图2所示。在图2示布尔矩阵下,构造NRT时,由于陪集4CO是陪集3CO及其所有父辈陪集的右邻居,所以4CO 可以作为3CO 的子陪集,而5CO尽管是4CO的右邻居但不是4CO所有父辈节点的右邻居,所以不能作为4CO的子陪集。最终,将长度最大的MaxPath作为势最大的可用陪集集合。
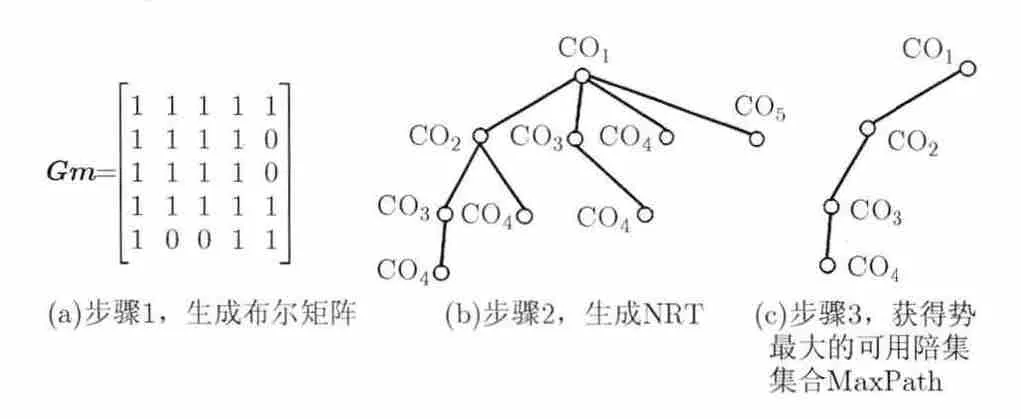
图2 树形深度优先搜索算法示意图
4 典型结果及性能仿真
根据上述方法,表2给出了典型母码下的最小陪集间汉明距离和抗比特泄露能力,及最小陪集间汉明距离下的最多可用陪集集合。其中*e为允许泄露的最多bit数,其值越大抗窃听信道信息泄露能力越强;为陪集间最小汉明距离,其值越大抗合法信道噪声性能越好;为在给定和条件下,势最大的部分陪集集合;为该部分陪集集合的势,即所包含的陪集数量。
将Wyner安全编码与基于部分陪集编码强安全编码进行仿真对比。以BPSK调制为例,假设合法信道为高斯白噪无线信道,功率谱密度为0N ,窃听信道为二进制纯擦除无线信道,擦除概率为ε,待传私密信息量m分别为3 bit, 4 bit。以本原BCH(15,11)的对偶码为部分陪集母码,各陪集中前( )n k- bit为0的元素作为陪集首,其对应的十进制值为相应的陪集序号。假设Bob和Eve均知道编译码方式。对于Wyner安全编码,在所有陪集中选取前2m个陪集作为可用陪集进行安全编码。对于部分陪集编码传递3 bit私密信息选取的可用陪集集合为:{0,95,679,826,1209,1477,1652,1738},其陪集间最小汉明距离为5;传递4 bit私密信息选取的可用陪集集合为:{0,79,181,371,632,667,742,908,1257,1309,1411,1534,1558,1834,1893,2000},其陪集间最小汉明距离为6。仿真结果如图3和图4所示。

表2 典型母码的部分陪集安全编码性能表
从图3可以看出,部分陪集编码方法的抗合法信道噪声性能优于传统的Wyner方法。这是因为传统陪集编码方案下,译码正确时当且仅当所有bit不发生传递错误,或者错成同一陪集内的码字。由于线性分组码任意码字间的汉明距离是另外一个码字的汉明重量,对于线性分组码,当传送的是全0码字时,其译码错误概率为

式中ep为译码错误概率,cp是译码正确概率,bp为bit错误概率,为码集合中第i个元素的汉明重量。以BCH(15,11)码为例,如果使用Wyner编码方案,为了保证合法接收者译码错误概率达到,则要求约为10 dB。部分陪集编码方案由于陪集间存在汉明距离,使得抗bit传输错误能力更强,信噪比要求更低。仿真结果表明,采用部分陪集编码方法当高于5 dB时误比特率趋近于0,相对于Wyner方法,对合法信道的信噪比要求降低了5 dB。又因为传递3 bit私密信息所选用的部分陪集间的最小汉明距离大于传递4 bit私密信息所选用的部分陪集间的最小汉明距离,因此传递3 bit私密信息时合法信道误比特率下降速度更快。
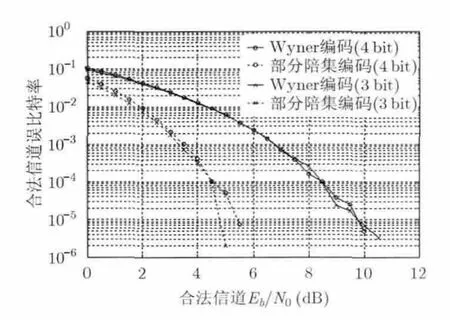
图3 合法信道误比特率随Eb/N0变化图
由定理1可知,以本原BCH(15,11)码的对偶码为母码的部分陪集编码方法,理论上能够保证Eve获得码字中的任意2 bit信息,即当窃听信道擦除概率高于时,能够满足式(1)所描述的强安全。图4的仿真结果表明,当擦除概率为0.87,进行部分陪集编码时的误比特率为0.497,接近误比特率为0.5的理论值,即能够保证私密信息的强安全传输。对于擦除概率为ε的窃听信道,不进行安全编码时理论误比特率为/2ε,该值比使用部分陪集编码方案时的误比特率低,这说明本文方法可以提高安全性。部分陪集编码方案和Wyner编码方法都是将每一个陪集对应一个待发送的私密消息。当陪集母码一样时,部分陪集编码方案和Wyner编码方法的抗信息泄露能力相同。然而,由于部分陪集编码选择陪集间汉明距离最大的陪集作为可用陪集,因此部分陪集编码比Wyner编码的抗噪声性能好。另外,由于所选用的部分陪集集合是相应最小陪集汉明距离要求下陪集元素最多的集合,因此其私密信息传输有效性也最高。
5 结束语
本文在深入分析陪集编码性质的基础上,提出了基于部分陪集的强安全编码方案,在保证私密信息强安全传输的同时,提高了其抗噪声性能。研究发现,部分陪集编码的强安全性、可靠性和有效性由陪集母码决定。我们下一步将针对部分陪集编码的强安全性、可靠性及有效性的内在关系进行深入研究。

图4 窃听信道误比特率随擦除概率变化图
[1] Wyner A D. The wiretap channel[J]. AT&T Bell Laboratories Technical Journal, 1975, 54(8): 1355-1387.
[2] Csiszár I and Körner J. Broadcast channels with confidential messages[J]. IEEE Transactions on Information Theory, 1978,24(3): 339-348.
[3] Ozarow L H and Wyner A D. Wire-tap channel Ⅱ[J]. AT&T Bell Laboratories Technical Journal, 1984, 63(10): 2135-2137.
[4] Cassuto Y and Bandic Z. Low-complexity wiretap codes with security and error-correction guarantees[C]. Proceedings of IEEE Information Theory Workshop, Dublin, 2010: 1-5.
[5] Belfiore J C and Oggier F. Lattice codes design for the Rayleigh fading wiretap channel[C]. Proceedings of IEEE International Conference on Communications Workshops,Kyoto, 2011: 1-5.
[6] Oggier F, Solé P, and Belfiore J C. Lattice codes for the wiretap Gaussian channel: construction and analysis[C].Proceedings of International Worshop Coding and Cryptology (IWCC): 3th International Workshop, Qingdao,China, 2011: 47-62.
[7] Thangaraj A, Dihidar S, Calderbank A R, et al.. Applications of LDPC codes to the wiretap channel[J]. IEEE Transactions on Information Theory, 2007, 53(8): 2933-2945.
[8] Klinc D, Ha J, Mclaughlin S W, et al.. LDPC codes for physical layer security[C]. Proceedings of IEEE Global Telecommunications Conference, Honolulu, 2009: 1-6.
[9] Liu R, Poor H V, Spasojevic P, et al.. Nested codes for secure transmission[C]. Proceedings of IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications, Cannes, 2008: 1-5.
[10] Andersson M. Coding for the wiretap channel[D]. [Ph.D.dissertation], Sweden: School of Electrical Engineering Royal Institute of Technology, 2011.
[11] Bloch M R. Achieving secrecy: capacity vs resolvability[C].Proceedings of IEEE International Symposium on Information Theory, Saint Petersburg, 2011: 632-636.
[12] Luzzi L. Capacity-based random codes cannot achieve strong secrecy over symmetric wiretap channels[C]. 5th Intermational ICST Conference on Performance Evaluation Methodologies and Tools, Paris, France, 2011: 641-647.
[13] 王亚东, 黄开枝, 吉江. 一种多天线信道特征投影物理层安全编码算法[J]. 电子与信息学报, 2012, 34(7): 1653-1658.Wang Ya-dong, Huang Kai-zhi, and Ji Jiang. A physical layer secrecy coding algorithm using multi-antenna channel characteristics projection[J]. Journal of Electronics &Information Technology, 2012, 34(7): 1653-1658.
[14] 殷勤业, 贾曙乔, 左莎琳, 等. 分布式多天线跳空收发技术Ⅰ[J]. 西安交通大学学报, 2013, 47(1): 1-8.Yin Qin-ye, Jia Shu-qiao, Zuo Sha-lin, et al.. A distributed multi-antenna space hopping transceiver technique Ⅰ[J].Journal of Xi’an Jiaotong University, 2013, 47(1): 1-8.
[15] Wen H, Ho P H, and Jiang X H. On achieving unconditional secure communications over binary symmetric channels(BSC)[J]. IEEE Wireless Communications Letters, 2012, 1(2):49-52.
[16] Mahdavifar H and Vardy A. Achieving the secrecy capacity of wiretap channels using polar codes[J]. IEEE Transactions on Information Theory, 2011, 57(10): 6428-6443.
