基于功率谱分段对消频谱感知算法研究及性能分析

齐佩汉司江勃 李 赞 高 锐

(西安电子科技大学综合业务网国家重点实验室 西安 710071)

1 引言

随着无线通信的快速发展，射频设备类型和数量剧增，频谱资源变得日益拥挤，无线信道质量逐渐恶化，在认知无线电[1]系统中，认知用户需要在没有主用户先验信息、无线信道衰落严重、噪声电平高动态变化的情况下，以极短的感知时间，找出频谱空穴，为新的无线应用提供高效的动态接入，这给经典的频谱感知算法带来了极大的挑战。

目前常用的频谱感知算法主要包括匹配滤波器检测法[2]、能量检测法[36]-、循环平稳检测法[7,8]以及特征值检测法[9,10]。匹配滤波器检测法可以最优地判断主用户的存在，但该算法不能进行盲频谱感知。能量检测法可分为时域能量检测算法和频域能量检测算法，但两者均不能摆脱噪声不确定度的影响。循环平稳检测法在未知主用户信号调制类型、码元速率和载波频率的情况下，需要计算出信号整个支集上的循环谱，算法计算复杂度高，不能满足实时频谱感知的要求。特征值检测算法以随机矩阵理论为原理，将接收信号相关矩阵最大与最小特征值的比值或者差值作为检验统计量，可以有效克服噪声不确定度的影响，但算法需要进行复杂的特征值分解运算，算法只能给出渐近的而非准确的判决门限。

为应对复杂电磁环境为频谱感知带来的新挑战，本文给出一种基于功率谱分段对消(Power spectral density Segment Cancellation, PSC)的频谱感知算法，该算法无需主用户的先验信息，具有克服噪声不确定度对信号检测性能影响的能力，适用于高斯白噪声和平坦慢衰落信道，可以为认知无线电系统实时提供频谱感知结果。本文余下内容组织如下：第2节给出PSC频谱感知算法的系统模型；第3节描述PSC算法的步骤；第4节在分析功率谱统计特性的基础上，推导出PSC算法的虚警概率、正确检测概率和判决门限的闭式表达式；第5节仿真验证PSC算法的性能，主要对PSC算法的抗噪声不确定度性能、衰落信道中的性能以及实时性进行了仿真和分析；第6节给出结论。

2 系统模型

认知无线电系统中，次级用户监测主用户可能出现的授权频段，利用授权频段中的空闲子带发送信息，次级用户接收到的信号[11]可表示为

3 PSC算法步骤

PSC算法利用0H和1H假设下周期图估计功率谱谱线分布的不同，完成对授权信号的存在性检测，图1给出了利用PSC算法进行信号检测的频谱感知器的组成框图，算法的详细步骤如下：

其中M为每帧中的样本数，T为所用帧数；

将式(4)和式(5)得到的每一组allS 和segS 进行分段对消，对消的比值为算法的检验统计量：

图1 功率谱分段对消频谱感知器

4 PSC算法性能分析

4.1 功率谱的统计特性

为方便分析次级用户接收信号周期图谱估计的统计特性，首先给出两条引理。

引理 2 互不相关随机变量的连续函数仍然互不相关[13]。

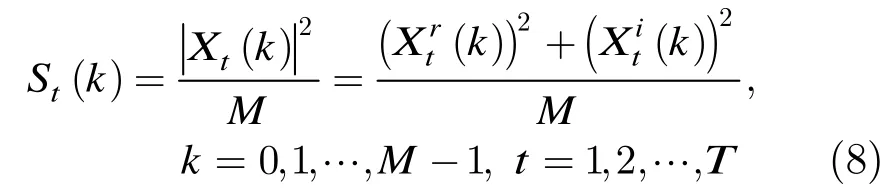
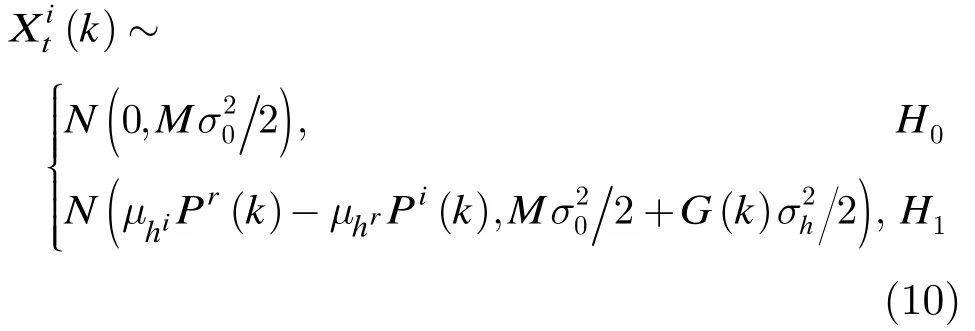
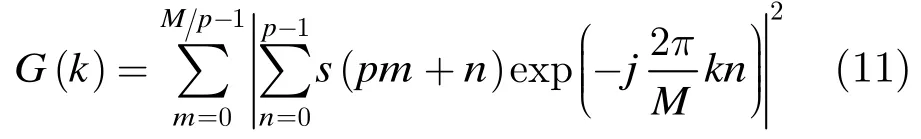
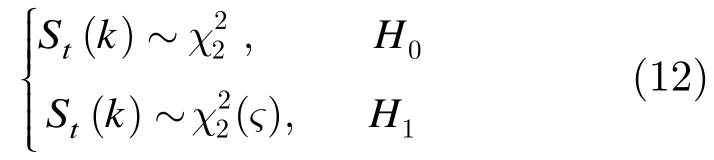
由引理 1性质(3)可知不同分帧数据在相同频点上的傅氏变换具有相互独立性，时间平均周期图谱估计的均值和方差可由的均值和方差通过线性运算得到，在 H0情况下,的均值和方差分别为和，在1H情况下，的均值和方差分别为和。

4.2 PSC算法虚警概率和判决门限

在0H 假设下，认知用户接收信号周期图功率谱估计值的均值和方差分别为，由式(13)得，中不同频点上的功率谱是互不相关的，构造随机变量和，根据中心极限定理，参与加和的功率谱频点足够多时(点数大于20)，可近似为服从高斯分布的随机变量，都大于零，并且和。PSC算法一组分段对消的虚警概率faP 可表示为

依据Neyman-Pearson准则，由预先设定的目标虚警概率求出每一组分段对消的虚警概率，将faP 代入式(14)，并令可以得到PSC算法门限值γ为

4.3 PSC算法检测概率

在1H假设下，功率谱平均值的均值为，方差为，其中由式(11)给出。构造随机变量和，由式(13)得，中不同频点上的功率谱是互不相关的，根据中心极限定理， ,X Y可近似为服从高斯分布的随机变量，均值和方差分别为

在Rayleigh衰落信道模型中，信道系数h为零均值复高斯随机变量，，实部和虚部服从相互独立的高斯分布，其均值为0，方差为，取归一化和，并将和分别代入和表达式中，可以得到，其中 ()G k由式(11)给出。在Rice衰落信道模型中，信道系数h为非零均值复高斯随机变量，,h的实部服从，虚部服从，莱斯因子可表示为，归一化选取，并将它们分别代入和的数学表达式中，可以得出。

5 算法仿真与结果分析

5.1 抗噪声不确定度性能

依据第2节描述的系统模型采用Monte Carlo方法对PSC算法进行性能仿真，并将其性能与能量检测算法性能进行对比。假设在 AWGN信道下，主用户发射调制信号，信号带宽为1.28 MHz，载波频率为5.12 MHz，次级用户未知主用户的调制类型和特征参数等先验信息，只能确定主用户会在内出现，因此，以采样速率对接收信号进行采样；定义噪声不确定度1ρ＞时，噪声方差在区间内均匀分布，不存在噪声不确定度时，噪声方差为定值，此时；对比能量检测(Energy Detection, ED)算法和功率谱分段对消(PSC)算法的检测性能时，采用恒虚警准则，预先设定虚警概率为0.01。

5.2 衰落信道下PSC算法性能

图 3对比了 AWGN信道模型和平坦慢衰落Rayleigh信道模型下，经典能量检测(ED)算法功率谱分段对消(PSC)算法的接收机性能(ROC)曲线，仿真参数配置为：接收序列帧数，每帧长度为，固定。图4仿真了平坦慢衰落Rice信道下，分别取莱斯因子,和, ED算法和PSC算法的ROC曲线，仿真参数配置与图3一致。

由图3和图4可见，ED算法和PSC算法在Rayleigh信道模型下的频谱感知性能略差于算法在AWGN信道模型下的感知性能，而在Rice信道模型下的频谱感知性能居于 Rayleigh信道模型和AWGN信道模型的感知性能之间，莱斯因子κ越小，算法的频谱感知性能越接近于Rayleigh信道模型下的频谱感知，莱斯因子κ越大，算法的频谱感知性能越接近于 AWGN信道模型下的频谱感知。利用式(17)-式(19)可以计算出 PSC算法 Rayleigh信道模型和 Rice信道模型下正确检测概率的理论值，通过仿真验证，仿真值与理论值基本一致。

5.3 PSC算法实时性分析

功率谱分段对消频谱感知器主要由模数转换单元、FFT变换单元、模平方运算单元、分段对消单元以及检测判决单元组成。模拟输入信号经过模数变换单元变成离散样本序列，每个样本点的转换时间为1 clk，4096个样本点需要4096 clk，而FFT变换单元调用 Altera公司的 FFT IP核[15]，采用Streaming Data Flow Engine Architecture架构，变换时间仅需要 4096 clk，每个复数的模平方运算需要1 clk, 4096点的模平方运算需要4096 clk，分段对消单元需要4096 clk完成各分段功率谱以及所有功率谱的累加，检测判决单元需要2 clk给出判决结果，其中1 clk进行对消计算，1 clk完成检验统计量与门限的比较，其中1 clk为一个主时钟周期。

若仅执行一次帧数为1，帧长为4096的功率谱分段对消检测，大约需要 8196 clk，以 FPGA EP5SGXEA7H3F35C2为硬件平台，采用频率为370 MHz主时钟，则需要执行时间大约为22.16 μs，若连续执行功率谱分段对消检测，在FPGA内部采用流水线架构，各运算单元并行处理数据，除了首次运行PSC频谱感知器，大约需要8196 clk，以后的每次感知，只需要 4096 clk，采用主时钟为 370 MHz，则执行需要时间大约为11.08 μs。类似于PSC频谱感知算法时间开销的分析，执行一次帧数为1，帧长为4096的经典能量频谱感知，需要时间大约为11.08 μs。经典能量频谱感知算法具有良好的实时性，而分段对消频谱感知算法采用FFT IP核以及流水线架构，也可以达到实时频谱感知的要求，但这是以增加空间复杂度、占用大量硬件资源为代价。

图2 PSC检测算法和ED算法正确检测概率对比示意图

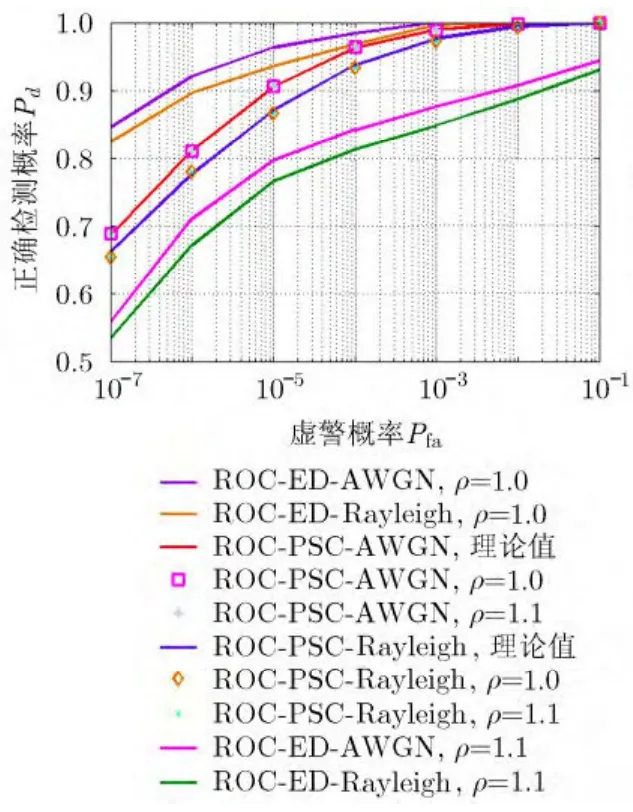
图3 PSC检测算法、ED算法在AWGN和 Rayleigh信道下正确检测概率对比示意图

图4 PSC检测算法和ED算法在Rice信道下正确检测概率对比示意图

结合上述章节PSC频谱感知算法与ED频谱感知算法在抗噪声不确定度、衰落信道感知性能、时间复杂度(实时性)以及空间复杂度(逻辑资源开销)分析，将两种算法的对比结果汇总如表1所示。

6 结束语

功率谱分段对消算法是为应对认知无线电系统频谱感知技术面临的新挑战而提出的一种算法，该算法的判决门限与参与运算的帧数、分段内的谱线数以及虚警概率有关，与噪声方差和噪声电平无关，其检测性能不受噪声不确定度的影响，该算法适用于加性高斯白噪声和平坦慢衰落信道模型，可以通过执行快速FFT运算达到实时检测的要求，因此，功率谱分段对消频谱感知算法可广泛应用于复杂电磁环境下的认知无线电系统中。利用功率谱分段对消算法进行频谱感知不仅可以获得带宽内是否存在主用户，还可以获得带宽内各频率子带的占用情况，该算法可为认知无线电系统在超宽带范围内进行多主用户频谱感知提供一种解决方案。

表1 PSC检测算法和ED算法分析对比表

[1] Sun Hong-jian and Nallanathan A. Wideband spectrum sensing for cognitive radio networks: a survey[J]. IEEE Wireless Communications, 2013, 20(2): 74-81.

[2] Eldar Y and Oppenheim A. Orthogonal matched filter detection[C]. IEEE International Conference on Acoustics,Speech, and Signal Processing-Proceedings. Saltlake, USA,2001: 2837-2840.

[3] Kyungtae K, Yan Xin, and Sampath R. Energy detection based spectrum sensing for cognitive radio: an experimental study[C]. Proceedings 2010 IEEE Global Communications Conference, Miami, USA, 2010: 1-5.

[4] Sofotasios P and Rebeiz E. Energy detection based spectrum sensing over -κμand -κμ extreme fading channels[J].IEEE Transactions on Vehicular Technology, 2013, 62(3):1031-1040.

[5] Gismalla E. A generalized system model and performance analysis for the periodogram-based energy detector[C].IEEE Global Communications Conference, Piscataway, USA,2011: 1-5.

[6] Alsusa E. An accurate model for periodogram-based energy detection over Nakagami fading[C]. IEEE International Conference on Communications, Ottawa, Canada, 2012:1614-1618.

[7] Enserink S and Cochran D. A cyclostationary feature detector[C]. Conference Record of the 28th Asilomar Conference on Signals, Systems and Computers, Los Alamitos, USA, 1994: 806-810.

[8] Rebeiz E, Urriza P, and Cabric D. Experimental analysis of cyclostationary detectors under cyclic frequency offsets[C]. Conference Record of the 46th Asilomar Conference on Signals, Systems and Computers, Piscataway, USA, 2012:1031-1035.

[9] Kortun A, Ratnarajah T, and Sellathurai M. Throughput analysis using eigenvalue based spectrum sensing under noise uncertainty[C]. International Wireless Communications and Mobile Computing Conference,Piscataway, USA, 2012: 395-400.

[10] 王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J]. 电子与信息学报, 2010, 32(11): 2571-2575.Wang Ying-xi and Lu Guang-yue. DMM based spectrum sensing method for cognitive radio systems[J]. Journal of Electronics ＆amp; Information Technology, 2010, 32(11):2571-2575.

[11] Herath S, Rajatheva N, and Tellambura C. Energy detection of unknown signals in fading and diversity reception[J].IEEE Transactions on Communications, 2011, 59(9):2443-2453.

[12] Chung Pei-jung and Bohme J. Detection of the number of signals using the Benjamini-Hochberg procedure[J]. IEEE Transactions on Signal Processing, 2007, 55(6): 2497-2508.

[13] Oppenheim A. Discrete-Time Signal Processing[M]. 3rd Ed,Upper Saddle River: Prentice Hall, 2010: 559-572.

[14] Zhang Ya-lin, Zhang Qin-yu, and Melodia T. A frequencydomain entropy-based detector for robust spectrum sensing in cognitive radio networks[J]. IEEE Communications Letters, 2010, 14(6): 533-535.

[15] Altera. FFT MegaCore Function User Guide[OL]. www.altera. com. 2012.11.