融合密度与邻域覆盖约简的分类方法
2022-06-07张清华艾志华张金镇
张清华, 艾志华, 张金镇
(重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065)
粗糙集是由Pawlak教授于1982年提出的一种处理不精确、不一致、不完全信息和知识的重要数学工具[1],已经被广泛应用于机器学习、知识发现、数据挖掘、决策支持与分析等[2-3]。但是Pawlak粗糙集只适用于处理离散型数据,对于实际应用中普遍存在的数值型或混合型数据,需要将其离散化,从而不可避免地带来了信息损失[4],从而影响分类效果。为解决这一问题,Pawlak粗糙集被扩展到邻域粗糙集[5]和模糊粗糙集[6-7]。实际上,邻域粗糙集提供了一种构造数据空间的近似方法[8]。从拓扑学的角度,证明了邻域空间比数据空间的概念更一般化[9],这表明将原始数据空间转化为邻域空间有助于数据的泛化[10],因此邻域粗糙集模型被广泛应用于分类学习[11-12]与特征选择[13-15]中。为了构造邻域空间,可以通过邻域粗糙集构造邻域覆盖,在邻域覆盖中,每个邻域中的样本都是同种类别的,因此邻域覆盖提供了一个从邻域层次去表示数据分布[16]的方法。并且,为了更精确地表示数据分布,邻域覆盖约简算法通过集合包含关系剔除冗余的邻域[17]。
由于邻域中所有样本都是同种类别的,所以每个邻域都对应一个分类规则。因此,文献[17]提出了基于邻域覆盖约简的规则学习方法(NCR),该方法通过邻域覆盖约简过滤掉冗余的邻域得到分类规则,进而根据离测试样本最近的邻域来匹配规则对测试样本分类。由于NCR方法简单、有效,被广泛应用于数据分类中,但该方法对邻域的约简过于严格,易受到噪声样本影响,从而在覆盖中仍然存在一些冗余的邻域,对规则提取带来较高的复杂度。另外,仅靠距离最近的邻域对测试样本分类可能会导致分类错误。针对上述问题,文献[18]基于三分法,通过控制邻域半径大小将邻域扩展到内邻域和外邻域,减少了在形成邻域时噪声样本的影响;文献[19]将邻域覆盖扩展到模糊邻域覆盖,提出了基于模糊邻域覆盖的三支决策分类方法;文献[20]基于行列式点过程,提出了一个新的邻域覆盖约简方法,有效地约简了冗余的邻域,能在更少的邻域下形成数据空间下的覆盖;文献[21]通过样本间的相似度构建邻域,然后采用邻域覆盖约简得到代表样本,进而通过代表样本对测试样本分类;文献[22]结合阴影集构造了阴影邻域,并提出了三支决策分类规则,有效地降低了不确定样本的分类风险;另外,文献[23]通过随机化属性约简,得到多组属性集合,在不同组的属性集合上采用邻域覆盖约简的方法学习分类规则,有效地提高了分类精度。
然而,现有大部分基于邻域覆盖的分类方法直接根据最近的邻域对测试样本进行分类,由于不同样本形成的邻域是不同的,且噪声样本形成的邻域中对象较少且离中心点较远,那么此类样本形成的邻域分类能力更弱。因此,仅通过最近的邻域对样本分类,忽略了邻域中其他样本的信息,没有考虑到邻域间的差异,容易受到噪声样本的影响。本文首先通过邻域中心和邻域中其他样本的距离计算出邻域中心的局部密度[24-25],用其代表整个邻域的局部密度,去刻画邻域之间的差异性。并且,邻域中的样本越多、越紧密,邻域的密度就越大,那么此种邻域的分类能力越强。然后将邻域中心的局部密度转化为权重,定义了测试样本到邻域中心的加权距离,并对处于不同位置的测试样本分别定义了内部样本点和外部样本点。最后基于加权距离,对两类点采用了不同的分类策略。实验结果验证了本文方法的优势及有效性。
1 基础知识
1.1 决策系统
定义1[21,26]决策系统可以表示为一个三元组
S=(U,A,D)。
(1)
式中:U是一个有限非空的样本集合,称为论域;A和D分别是有限非空的条件属性集合和决策属性集合。
一般地,一个简单的决策系统如表1所示,其中U={x1,x2,…,x13},A={a1,a2},D={d}。在分类任务中,常常把论域切分成训练样本集Utrain和测试样本集Utest。
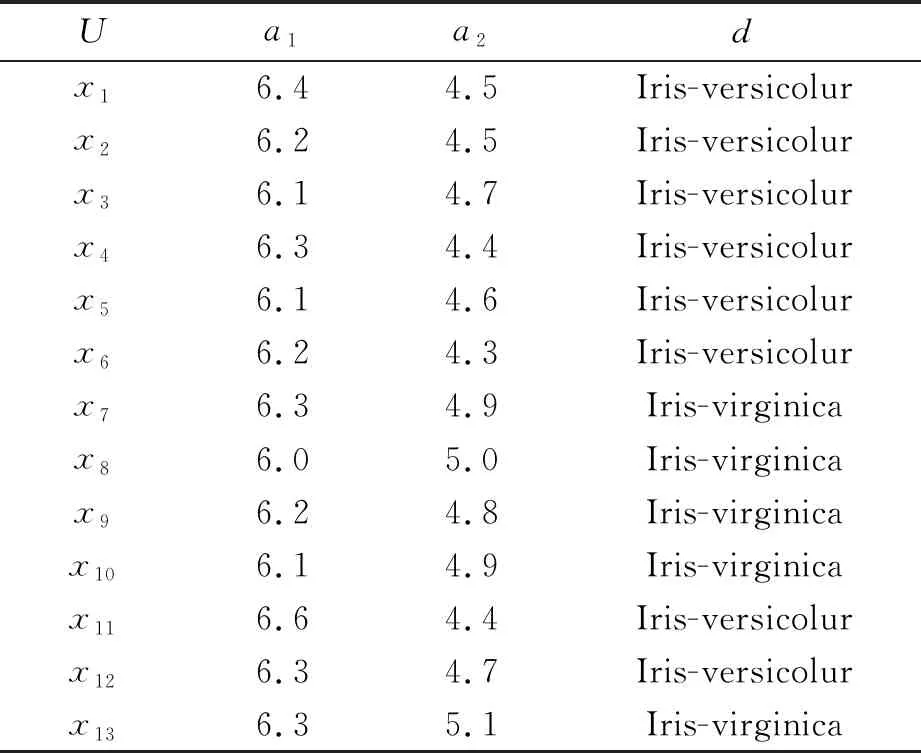
表1 决策系统
1.2 邻域覆盖模型
邻域覆盖是同类邻域的集合,从而为数据分布提供了一个集合水平上的近似[27-28]。由于邻域覆盖模型非参数的特性和对复杂数据的鲁棒性,邻域覆盖模型已经被广泛应用于数据挖掘任务中,如分类[17-23]、特征选择[29-31]等。邻域覆盖的定义如下。
定义2[17,19]设U={x1,x2,…,xn}是一个论域,且O(xi)={y∈U|Δ(xi,y)≤r(xi)}表示样本xi的邻域,其中Δ(·)是一个距离函数,r(xi)表示样本xi的半径。则邻域集合O={O(xi)|xi∈U}形成了论域U上的一个覆盖,且C=〈U,O〉表示邻域覆盖近似空间。
显然,在邻域覆盖中,可能存在一些邻域是相互重叠的,因此在维持数据空间结构的过程中,某些重叠的邻域可以进一步被约简。邻域覆盖约简使得提取的数据空间结构具有更小的数据冗余性。给出邻域覆盖约简的定义如下。
定义3[17,19]设C=〈U,O〉是一个邻域覆盖近似空间,如果∀xi∈U,有∪y∈U-{xi}O(y)=U,那么O(xi)就是可约简的,否则就是不可约简的。如果在C中的所有邻域都是不可约简的,那么C就是不可约简的。
为了进一步近似同类样本的数据分布,相对邻域覆盖约简的定义如下。
定义4[17,19]设C=〈U,O〉是一个邻域覆盖近似空间,X⊆U是一个样本集合且O(xi)∈O是一个邻域,如果∃O(xj)∈O且i≠j,使得O(xi)⊆O(xj)⊆X,那么O(xi)就是对于X相对可约简的邻域,否则O(xi)就是相对不可约简的。如果在C中的所有邻域都是相对不可约简的,那么C就是相对不可约简的。
对于同一类数据,通过相对邻域覆盖约简,可以得到该类数据分布的近似,进而得到整个数据的近似分布,从而可用于数据分类任务中。
2 一种融合密度与邻域覆盖约简的分类方法
本节首先详细地介绍邻域覆盖的构建及邻域覆盖约简算法,然后给出基于密度的两种分类策略,最后提出融合密度与邻域覆盖约简的分类方法。
2.1 邻域覆盖的构建
邻域通过样本之间的距离或者相似度来构建。常用的距离公式有欧式距离、闵可夫斯距离等;常用的相似度公式有余弦相似度、Jaccard相似系数等。但是,对于实际场景普遍存在的数值型属性和名义型属性的混合属性数据,本文采取混合欧式距离重叠度量[32](HEOM)去衡量样本间的距离,HEOM距离函数利用重叠法针对数值型和名义型数据进行度量,还可以为欧式距离计算后的数据样本进行归一化处理。因此,∀x,y∈U,在m个属性下HEOM距离函数定义为
(2)
式中:dai(x,y)表示在属性ai下样本x和y的距离。dai(x,y)的距离定义为
(3)

因此,对于一个样本集合U={x1,x2,…,xn},可以通过样本间的HEOM距离构建邻域。给定样本xi∈U,邻域O(xi)={y∈U|Δ(xi,y)≤r(xi)}由邻域中心xi附近的样本组成,Δ(·)是HEOM距离函数,r(xi)表示样本xi的邻域半径。为了保证邻域中样本都是同种类别,样本xi的邻域半径r(xi)与它最近的同类和异类样本有关[17,19]。设NH(xi)是样本xi最近的同类样本(如果某类只有一个样本,则NH(xi)=xi),NM(xi)为样本xi最近的异类样本,则样本xi的邻域半径r(xi)=Δ(xi,NM(xi))-c×Δ(xi,NH(xi)),其中c是一个常数,控制邻域半径大小,在实验中c=0.01。显然,由xi形成的邻域中所有样本是和xi同类别的。
对于一个样本集合U={x1,x2,…,xn},邻域集合O={O(xi)|xi∈U}形成了论域U上的一个覆盖。由于邻域覆盖中可能包含冗余的邻域,从而对分类规则提取造成很高的复杂度。因此,根据定义2和3,通过邻域覆盖约简[17],约简冗余的邻域。邻域覆盖约简算法从一个空集开始,采用前向搜索策略,每次添加一个邻域。在每一步迭代中选择覆盖样本最多的邻域,而被当前覆盖样本最多的邻域所包含的邻域会被约简,依次迭代,直到初始邻域覆盖为空。从而得到约简后的前h个的邻域集合Or={O(x1),O(x2),…,O(xh)}[17]。
例1在表1中,论域U={x1,x2,…,x13},将论域U切分为训练样本集Utrain={x1,x2,…,x10}和测试样本集Utest={x11,x12,x13}。因此,可以计算出每个测试样本的邻域半径以及形成的邻域(如表2所示),得到初始邻域覆盖如图1所示,进而通过邻域覆盖约简算法[17]对冗余的邻域进行约简,由于邻域O(x2)、O(x4)和O(x6)中均覆盖6个样本,因此在约简中随机选取邻域O(x2)作为最终约简后的邻域。邻域O(x2)、O(x4)和O(x6)均能刻画出数据分布,对模型的训练没有影响,且对最后的分类效果影响较小。因此,约简后得到最终的邻域集合Or={O(x2),O(x7),O(x10)}如图2所示。

表2 训练样本的半径及邻域

图1 初始邻域覆盖
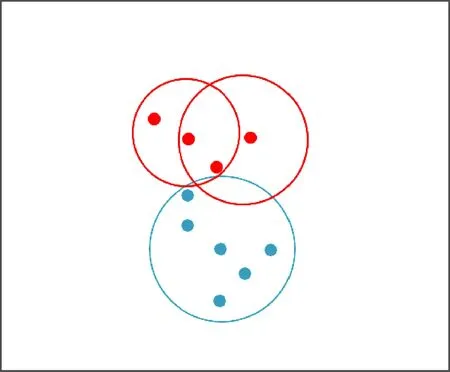
图2 约简后的邻域覆盖
2.2 基于密度的分类策略
在邻域覆盖中,由于邻域中的样本都是同类的,因此每一个邻域都对应一个分类规则。在NCR[17]分类时,将测试样本分类给最近邻域所在的类,这样仅考虑了邻域中心的信息,邻域中其他样本的信息被忽略,这种分类方式很容易受到噪声样本的影响,而造成分类错误。因此,本文引入了局部密度,通过局部密度刻画邻域中其他样本的信息,再将邻域中心的局部密度转化为权重,定义了测试样本和邻域中心之间的加权距离,最后对不同情况下的测试样本提出2种分类策略。
为了刻画邻域之间的差异性,受到文献[24]中密度峰值思想的启发,即通过样本周围的样本数量,以及相互之间的距离来描述样本的重要性,本文借助此思想计算邻域中心(样本)的重要性来刻画邻域间的差异。但与文献[24]定义不同的是,本文的样本半径是自适应变化的,并不需要人为设定。因此,给出局部密度的定义如下。
定义5给定约简后邻域集合Or,∀O(xi)∈Or,则邻域中心xi的局部密度为
(4)
且归一化后xi的局部密度为
(5)
式中:r(xi)为样本xi的邻域半径。
从公式(4)、(5)可以看出,邻域中的样本越多,样本离邻域中心越近,那么该邻域中心的局部密度就越大。值得注意的是,当邻域中没有其他样本时,则该邻域中心的局部密度为0,一般这类邻域是由噪声样本所形成的邻域。
对于一个测试样本,可以分为3种情况:1)处于一个邻域之中;2)处于多个邻域之中;3)不处于任意邻域之中。
因为在邻域集合Or中每个邻域都对应着一个分类规则,所以对于前2种情况都有相应的分类规则与之匹配,而第3种情况没有对应的分类规则匹配。因此,针对不同情况下的测试样本,本文采取了不同的分类策略。为了方便叙述,本文分别定义了外部样本点和内部样本点。
定义6给定一个测试样本s和约简后邻域集合Or,如果∀O(xi)∈Or,使得Δ(s,xi)>r(xi),则称测试样本s为邻域集合Or上的外部样本点,简记为外部点。
定义7给定一个测试样本s和约简后邻域集合Or,如果∃O(xi)∈Or,使得Δ(s,xi)≤r(xi),则称测试样本s为邻域集合Or上的内部样本点,简记为内部点。
定义8给定一个测试样本s和约简后邻域集合Or,那么样本s和∀O(xi)∈Or的加权距离为
(6)
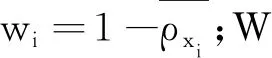
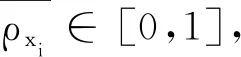
基于加权距离,分别对内部点和外部点采取不同的分类策略,分类策略详细描述如下所示。
样本分类策略1针对外部点进行分类。
假设测试样本s为邻域集合Or上的外部点,由于外部点s不处于任何一个邻域,没有分类规则进行分配,因此需要计算所有邻域中心和外部点s的加权距离,最后选择离外部点s加权距离最小的一个邻域对其分类。即
(7)
样本分类策略2针对内部点进行分类。
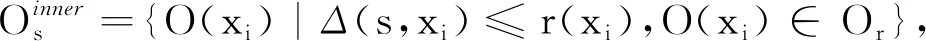
(8)
(9)

最后,选择加权距离最小的邻域对样本s分类,即
(10)
2.3 算法设计
基于前文中的样本分类策略,本文D-NCR如算法1所示。

算法1 融合密度与邻域覆盖约简的分类方法
输入:邻域集合Or,测试样本s。
输出:测试样本s的类别。
初始化O*←∅。

根据公式(4)计算Or中邻域中心的局部密度。

通过公式(5)对Or中所有邻域的密度进行归一化。
通过公式(6)计算出离样本s最近的邻域
else/*测试样本s为内部点*/。

O*←O(xi)。

通过公式(9)计算出离样本s最近的邻域
end if。
end if。

将邻域O*的类标签分配给测试样本s。
例2(续例1)由例1得出的邻域集合Or={O(x2),O(x7),O(x10)}和测试样本集合Utest={x11,x12,x13}形成的图像如图3所示。根据算法1,通过Or对测试样本集Utest={x11,x12,x13}中的样本分类,分类步骤如下。
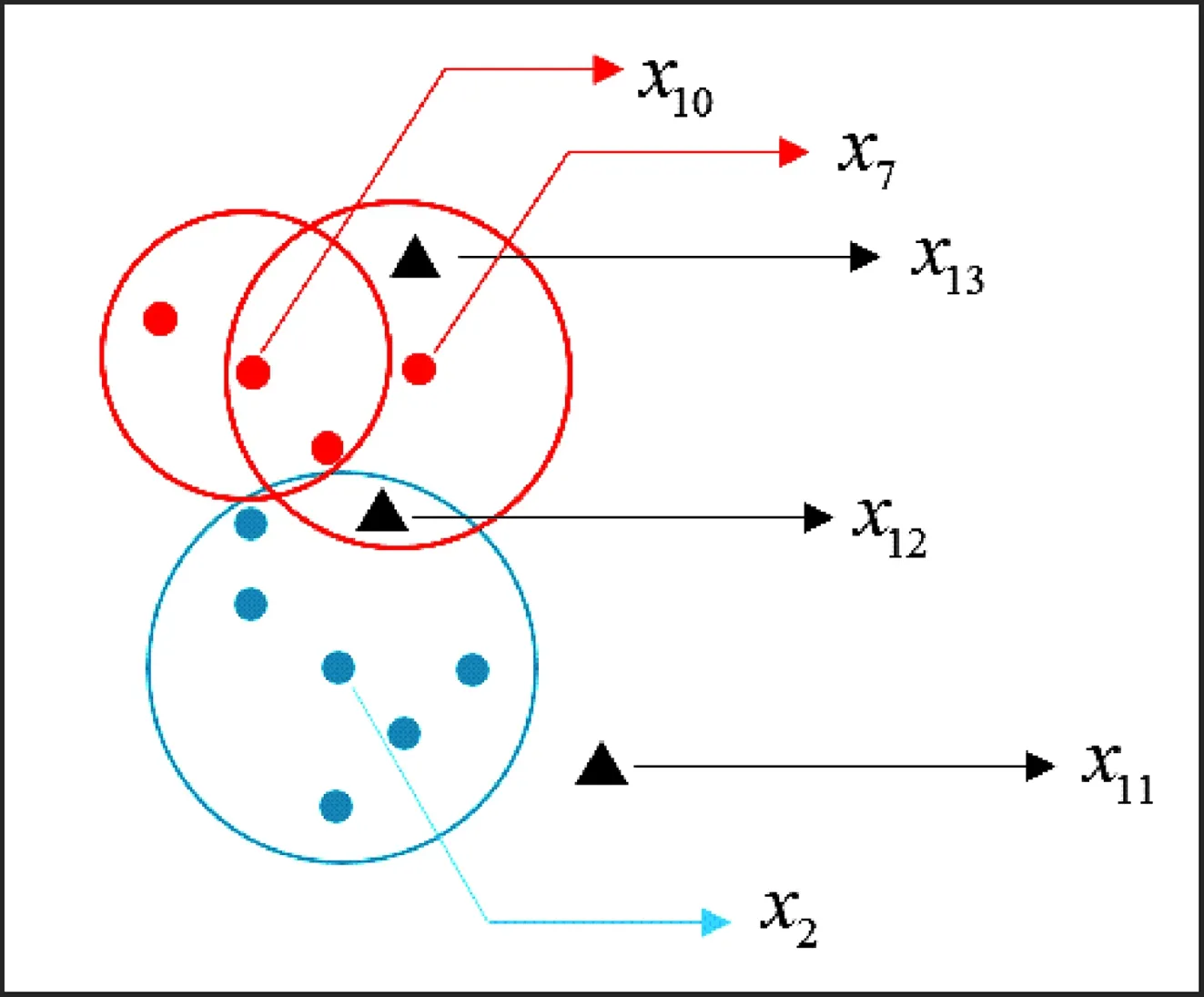
图3 测试样本和邻域集合Or
步骤一计算测试样本和所有邻域中心的距离。
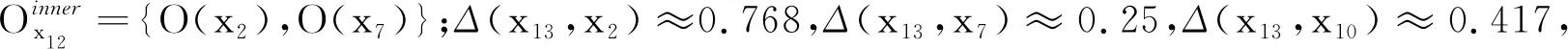
步骤二计算Or中所有邻域中心的局部密度。
ρx2≈3.074,ρx7≈1.301,ρx10≈0.987。
步骤三对测试样本进行分类。
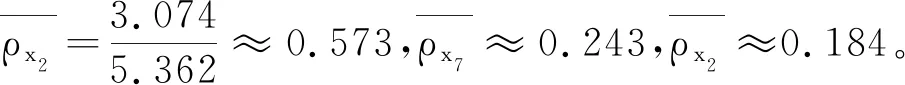
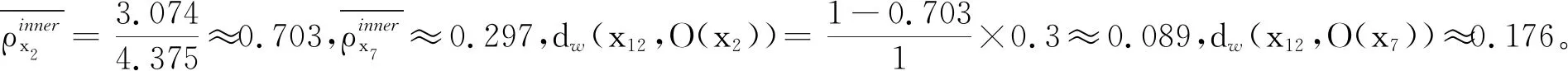
对于x13,由于x13只存在于O(x7)中,即x13是内部点且只存在于单个邻域中,因此将O(x7)的类标签(Iris-virginica)分配给x13。
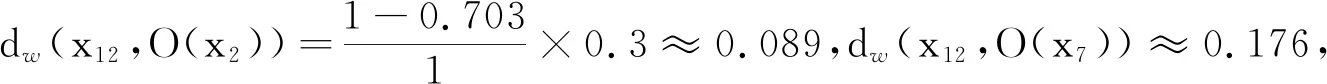
3 实验分析
为了进一步阐述本文D-NCR的优势,分别在UCI的10个数据集进行实验,数据集详细信息如表3所示。对比算法有NCR[17]、TNCR[18]、邻域分类器[12](NEC)、K近邻(KNN)、朴素贝叶斯(NB)和决策树(CART)。实验采用10折交叉验证,实验环境为Windows 10操作系统,16 GiB内存,3.60 GiHz主频,编程语言采用Python。

表3 实验数据集
3.1 评估指标
为了直观地展示实验结果,本文采用的评价指标有准确率(A)、精确率(PC)、召回率(R)和F1值[33-34]。给定一个数据样本集合,设P表示正例的个数,N表示负例的个数,TP表示正确地预测为正例的个数,FP表示错误地预测为正例的个数,TN表示正确地预测为负例的个数,FN表示错误的预测为负例的个数,那么
(11)
(12)
(13)
(14)
3.2 实验结果与分析
分两部分进行对比分析,第一部分为D-NCR、TNCR[18]、NCR[17]进行对比,第二部分为D-NCR和其他分类算法进行对比。每个数据集下评价指标的最优结果用加粗表示。
3.2.1 D-NCR与NCR、TNCR对比
为了体现本文D-NCR的优势,分别与TNCR和NCR进行对比。在10个数据下4种指标的实验结果如表4所示。

表4 D-NCR、TNCR和NCR在4种指标下的分类结果
相较于NCR,本文D-NCR通过局部密度刻画邻域之间的差异性,能更好地利用样本信息进行分类。TNCR尽管能通过异质率减少受到噪声点的影响,但是TNCR中的完全三分邻域覆盖约简中的约简规则较严格,导致约简后邻域集合中的邻域仍然有较多重叠,使得模型的复杂度提高,影响最后模型的分类效果。且由表4可以发现,相较于NCR,D-NCR在4个指标下在Credit数据集分类效果与NCR基本一致,在其他9个数据集上均有相应幅度的提升。在Credit数据集上,约简后邻域中心的局部密度大部分相差不大,从而邻域的权重也几乎一致,导致分类效果和NCR基本一致。在平均指标下,D-NCR在10个数据集下分别较NCR提升1.82%、0.81%、2.02%、1.87%。相较于TNCR,D-NCR能在大多数数据集下达到最优的效果,且在平均指标下,D-NCR在10个数据集下分别较NCR提升1.33%、0.49%、2.49%、2.52%。
在时间复杂度上,相较于NCR,D-NCR需要花费一定时间计算约简后所有邻域中心的局部密度,从而得出测试样本到邻域中心的加权距离,但时间复杂度和NCR一致,均为O(n2)。
综上,相比于NCR,本文提出的D-NCR在时间复杂度不变的情况下有更好的分类效果。
3.2.2 D-NCR与其他分类算法对比
为了进一步体现本文D-NCR的优势,分别与NEC、CART、NB、KNN分类器进行对比,在10个数据下4种指标的实验结果如表5~8所示。

表5 不同算法的准确率

表6 不同算法的精确率

表7 不同算法的召回率
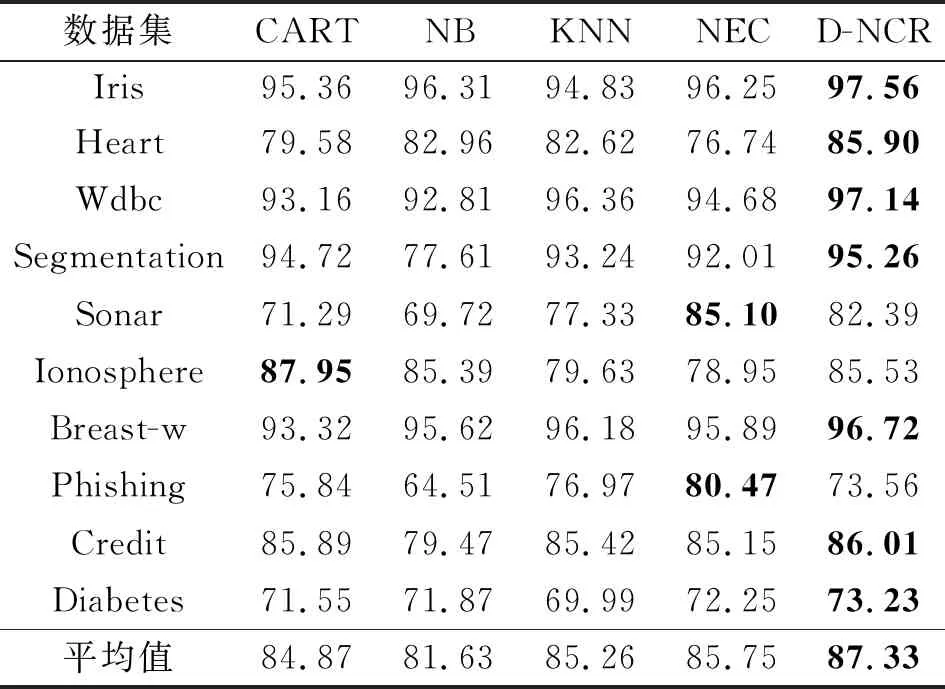
表8 不同算法的F1
NEC的核心参数是δ,Hu等通过
δ=min(Δ(xi,s))+ω·range(Δ(xi,s)),ω≤1
来控制邻域的半径,且得出ω=0.1左右时达到较好的分类效果[12],因此本实验中NEC的ω值取0.1,KNN中K取10。相较于KNN,由于NEC分类器能够随数据分布的变化来动态变化半径值,因此在实验结果上有略微的提升。虽然D-NCR、NEC、KNN能实现更好的分类结果,但是NEC、KNN在不同分布下的数据容易受到参数的影响。由于在D-NCR中可以通过多个邻域去表示数据分布,因此相较于CART、NB、KNN和NEC,D-NCR在Iris、Heart、Wdbc、Segmentatio、Breast-w、Diabetes 6个数据集上能达到最优的效果,在其他数据集上也能有次优的效果,且在10个数据集上平均分类精度、准确率、召回率和F1,D-NCR都能达到最优的分类效果。实验数据表明,本文提出的D-NCR优于其他一些分类算法。
4 结语
NCR直接根据最近的邻域对测样样本进行分类,未考虑邻域之间的差异,容易受到噪声样本形成邻域的影响,从而造成分类错误。针对此问题,本文提出了融合密度与邻域覆盖约简的分类方法D-NCR。由于噪声样本形成的邻域中样本少且离邻域中心远,此类样本形成的邻域的分类能力更弱,因此通过局部密度刻画邻域中样本的信息,并将局部密度转化为权重,得到测试样本和邻域中心之间的加权距离,通过加权距离,不仅考虑了测试样本到邻域中心的距离,而且考虑了邻域之间密度的差异性,充分利用了邻域中其他样本的信息。并基于加权距离,对不同的测试样本提出2种分类策略。在UCI数据集上的实验结果表明了本文方法的有效性。在大数据场景下,研究更加高效的算法是未来的研究重点。
